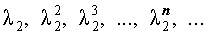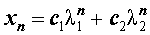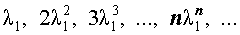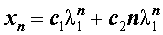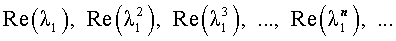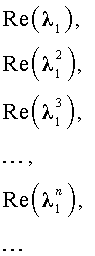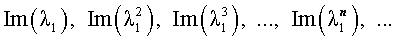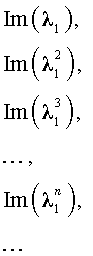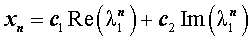Как решать рекуррентные уравнения

Рекуррентные соотношения и уравнения

В этом разделе вы найдете бесплатные примеры решений рекуррентных соотношений методом характеристического уравнения и подбора частного решения по правой части. Также приведены краткие алгоритмы решения для двух методов и пример их использования для последовательности Фибоначчи.

Как решать рекуррентные соотношения?

Для решения рекуррентных соотношений применяют один из двух основных способов:

В следующем разделе мы сравним, как выглядит процесс решения для одной и той же последовательности двумя методами.

Метод производящих функций

Метод характеристических функций

Этот метод практически полностью аналогичен методу решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, кратко алгоритм выглядит так:

Решение для последовательности чисел Фибоначчи

Общая формула данной рекуррентной последовательности имеет вид6

Способ 1. Производящяя функция

$$\begin 1\cdot f_0 &= &0\cdot 1,\\ z\cdot f_1 &= &1\cdot z,\\ z\cdot f_n & = &(f_+f_)\cdot z^n, \quad n\geq2.\\ \end $$

Складываем все строчки:

На третьем шаге алгоритма приводим все суммы к замкнутому виду:

откуда выводим искомое выражение для производящей функции:

Теперь разложим ее в степенной ряд. Для этого сначала разложим знаменатель на множители. Найдем корни уравнения:

Чтобы разложить данные дроби в ряды, используем известное разложение для дроби:

Преобразуем данное выражение, используя то, что

Способ 2. Характеристическое уравнение

Тогда общее решение однородного рекуррентного уравнения имеет вид:

Решая систему, найдем

Итоговое выражение для последовательности чисел Фибоначчи:

Результаты обоих методов совпали, решение вторым методом оказалось проще и короче.

Примеры решений

Источник

Решение рекуррентных соотношений

Содержание

Определения [ править ]

[math] F_0 = 0,\qquad F_1 = 1,\qquad F_ = F_ + F_, \quad n\geqslant 2, \quad n\in Z[/math]

Для этого можно использовать метод производящих функций (англ. generating function method).

Метод производящих функций [ править ]

Примеры [ править ]

[math]1[/math] пример [ править ]

Производящие функции позволяют решать рекуррентные соотношение механически по одному и тому же алгоритму. Рассмотрим общую схему на простом примере, который позволит продемонстрировать базовые приёмы работы.

Задано линейное однородное рекуррентное соотношение порядка [math]2[/math] с постоянными коэффициентами:
[math]\begin a_0&<>=<>&0,\\ a_1&<>=<>&1,\\ a_n&<>=<>&5a_-6a_, \quad n\geqslant2.\\ \end [/math]

Будем искать производящую функцию последовательности в виде
[math] G(z)=\displaystyle\sum_^ <\infty>a_nz^n = a_0+a_1z+a_2z^2+\cdots, [/math]

Теперь сложим все уравнения для всех значений [math]n[/math] :
[math] \underbrace^<\infty>a_nz^n>_ <=>z+5\displaystyle\sum_^<\infty>a_z^n-6\displaystyle\sum_^<\infty>a_z^n. [/math]

Аналогичные манипуляции со второй суммой дают нам выражение
[math] \displaystyle\sum_^<\infty>a_z^n = z^2\displaystyle\sum_^<\infty>a_z^ = z^2\displaystyle\sum_^<\infty>a_z^=z^2G(z). [/math]

откуда получаем производящую функцию последовательности в замкнутом виде:
[math] G(z) = \dfrac<1-5z+6z^2>. [/math]

Теперь разобьём дробь на сумму простых дробей:
[math] \dfrac <(1-3z)(1-2z)>= \dfrac<1> <1-3z>— \dfrac<1><1-2z>. [/math]

Из этого разложения следует, что
[math] \dfrac<1><1-3z>= \displaystyle\sum_^<\infty>(3z)^n \quad\mbox< и >\quad \dfrac<1><1-2z>= \displaystyle\sum_^<\infty>(2z)^n. [/math]

С другой стороны, мы искали [math]G(z)[/math] в виде
[math] G(z)=\displaystyle\sum_^ <\infty>a_nz^n, [/math]
поэтому, в силу равенства рядов, [math]a_n=3^n-2^n[/math] (для [math]n\geqslant 0[/math] ).

[math]2[/math] пример: числа Фибоначчи [ править ]

Рассмотрим рекуррентное соотношение для чисел Фибоначчи:
[math]\begin f_0&<>=<>&0,\\ f_1&<>=<>&1,\\ f_n&<>=<>&f_+f_, \quad n\geqslant2.\\ \end [/math]

Первый шаг алгоритма мы уже выполнили, записав рекуррентное соотношение. Выполним второй шаг:
[math]\begin 1\cdot f_0&<>=<>&0\cdot 1,\\ z\cdot f_1&<>=<>&1\cdot z,\\ z^n\cdot f_n&<>=<>&(f_+f_)\cdot z^n, \quad n\geqslant2.\\ \end [/math]

Складываем все строчки:
[math] f_0 + f_1 z + \displaystyle\sum_^<\infty>f_nz^n = z + \displaystyle\sum_^<\infty>f_z^n+\displaystyle\sum_^<\infty>f_z^n. [/math]

Третий шаг алгоритма требует привести все суммы к замкнутому виду:
[math]\begin G(z) &<>=<>& z + z\displaystyle\sum_^<\infty>f_z^+z^2\displaystyle\sum_^<\infty>f_z^, \\ G(z) &<>=<>& z + z\displaystyle\sum_^<\infty>f_z^n+z^2\displaystyle\sum_^<\infty>f_z^n, \\ G(z)&<>=<>& \displaystyle z + z(G(z)-f_0)+z^2G(z),\\ G(z)&<>=<>& \displaystyle z + zG(z)+z^2G(z),\\ \end [/math]

откуда получаем замкнутое выражение для производящей функции:
[math] G(z) = \dfrac<1-z-z^2>. [/math]

Осталось разложить её в ряд (чего требует четвёртый шаг алгоритма). С этой целью нужно разложить знаменатель на множители. Найдем корни уравнения:
[math]\displaylines< 1-z-z^2 = 0 \cr z_1=-\dfrac<1-\sqrt<5>><2>, z_2=-\dfrac<1+\sqrt<5>><2>. > [/math]

Нам известно разложение следующей рациональной функции:
[math] \dfrac<1> <1-z>= \displaystyle\sum_^<\infty>z^n = 1 + z + z^2 + z^3 + \cdots. [/math]

Рассмотрим первую дробь и поделим в ней числитель и знаменатель на [math]z_1[/math] :
[math] \dfrac = \dfrac1\dfrac<1><1-\dfrac> = \dfrac1\displaystyle\sum_^<\infty>\dfrac. [/math]

Аналогично (но с делением на [math]z_2[/math] ) поступим со второй дробью:
[math] \dfrac = \dfrac1\dfrac1<1-\dfrac> = \dfrac1\displaystyle\sum_^<\infty>\dfrac. [/math]

[math]3[/math] пример [ править ]

Рекуррентное соотношение:
[math] \begin a_0 = f_0^2 = 1 \\ a_1 = f_1^2 = 1 \\ a_2 = f_2^2 = 4 \\ a_n = 2a_ + 2a_ — a_, \quad n\geqslant3.\\ \end [/math]

[math]4[/math] пример [ править ]

Рассмотрим следующее рекуррентное соотношение:
[math]\begin a_0&<>=<>&1,\\ a_1&<>=<>&2,\\ a_n&<>=<>&6a_-8a_+n, \quad n\geqslant2.\\ \end [/math]

Вспомним, что
[math] (z^n)’ = nz^, [/math]

поэтому
[math] \displaystyle\sum_^<\infty>nz^n=z\displaystyle\sum_^<\infty>nz^=z\displaystyle\sum_^<\infty>(z^n)’=z\biggl(\displaystyle\sum_^<\infty>z^n\biggr)’. [/math]

Последняя сумма может быть свёрнута:
[math] \displaystyle\sum_^<\infty>z^n=\displaystyle\sum_^<\infty>z^n-1-z=\dfrac<1><1-z>-1-z=\dfrac<1-z>. [/math]

Подставив свёрнутое выражение обратно, имеем,
[math] z\biggl(\displaystyle\sum_^<\infty>z^n\biggr)’ = z \biggl(\dfrac<1-z>\biggr)’=\dfrac<(1-z)^2>. [/math]

Это уравнение для производящей функции. Из него выражаем [math]G(z)[/math] :
[math] G(z) = \dfrac<1-6z+11z^2-5z^3><(1-6z+8z^2)(1-z)^2>. [/math]

Дальше мы знаем что делать со всеми этими дробями, кроме, разве лишь, первой. Рассмотрим её (без множителя) подробнее:
[math] \dfrac<1> <(1-z)^2>=(1-z)^ <-2>=\displaystyle\sum_^<\infty>\binom<-2>(-z)^n=\displaystyle\sum_^<\infty>(-1)^n\binom<1>(-z)^n =\displaystyle\sum_^<\infty>(n+1)z^n. [/math]

Источник

Дискретная математика — рекуррентное соотношение

Определение

Рекуррентное отношение — это уравнение, которое рекурсивно определяет последовательность, в которой следующий член является функцией предыдущих членов (выражая F n как некоторую комбинацию F i с i n ).

Линейные рекуррентные отношения

Линейное рекуррентное уравнение степени k или порядка k — это рекуррентное уравнение в формате x n = A 1 x n − 1 + A 2 x n − 1 + A 3 x n − 1 + d o t s A k x n k ( A n — константа, а A k n e q 0 ) на последовательности чисел как полинома первой степени.

Вот некоторые примеры линейных рекуррентных уравнений —

Как решить линейное рекуррентное соотношение

Характеристическое уравнение для вышеуказанного рекуррентного соотношения —

Три случая могут возникнуть при поиске корней —

Характеристическое уравнение рекуррентного соотношения —

Итак, ( x − 3 ) ( x − 2 ) = 0

Корни реальны и различны. Итак, это в форме дела 1

F n = a x n 1 + b x n 2

Здесь F n = a 3 n + b 2 n ( A s x 1 = 3 a n d x 2 = 2 )

1 = F 0 = a 3 0 + b 2 0 = a + b

4 = F 1 = a 3 1 + b 2 1 = 3 a + 2 b

Решая эти два уравнения, мы получаем a = 2 и b = − 1

Следовательно, окончательное решение —

Характеристическое уравнение рекуррентного соотношения —

Следовательно, существует один действительный корень x 1 = 5

Поскольку существует единый действительный корень, он имеет вид случая 2

F n = a x n 1 + b n x n 1

Решая эти два уравнения, мы получаем a = 3 и b = 2 / 5

Характеристическое уравнение рекуррентного соотношения —

Источник

Возвратные последовательности:
рекуррентная формула, характеристическое уравнение

Определение возвратной последовательности

Характеристическое уравнение

Общее решение рекуррентного уравнения 2-го порядка

Схема вывода формулы общего члена возвратной последовательности второго порядка

Примеры с решениями

Определение возвратной последовательности

в каждой из которых символами b₁ и q обозначены заданные числа – первый член и знаменатель прогрессии.

а остальные члены последовательности определяются с помощью рекуррентной формулы (рекуррентного уравнения)

– заданные числа ( коэффициенты рекуррентной формулы ).

Характеристическое уравнение

удовлетворяет рекуррентной формуле (1).

то при подстановке формул (2) и (3) в формулу (1) возникает уравнение

которое удобно переписать в виде

Общее решение рекуррентного уравнения второго порядка

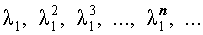
и

удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c₁ и c₂ последовательность с общим членом

также удовлетворяет рекуррентной формуле (1).

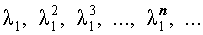
и

удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c₁ и c₂ последовательность с общим членом

также удовлетворяет рекуррентной формуле (1).

В случае, когда характеристическое уравнение имеет два комплексно-сопряженных корня λ_{1, 2} = α ± i β, каждая из последовательностей

удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c₁ и c₂ последовательность с общим членом

также удовлетворяет рекуррентной формуле (1).

Ряд примеров, в которых выводятся формулы общего члена возвратных последовательностей, разобран в разделе «Возвратные последовательности: вывод формулы общего члена» нашего справочника.

Источник

Производящие функции — туда и обратно

«Производящая функция является устройством, отчасти напоминающим мешок. Вместо того чтобы нести отдельно много предметов, что могло бы оказаться затруднительным, мы собираем их вместе, и тогда нам нужно нести лишь один предмет — мешок».
Д. Пойа

Введение

Математика делится на два мира — дискретный и непрерывный. В реальном мире есть место и для того и для другого, и часто к изучению одного явления можно подойти с разных сторон. В этой статье мы рассмотрим метод решения задач с помощью производящих функций — мостика ведущего из дискретного мира в непрерывный, и наоборот.

Идея производящих функций достаточно проста: сопоставим некоторой последовательности — дискретному объекту, степенной ряд g₀ + g₁z + g₂z 2 +… + g_nz n +… — объект непрерывный, тем самым мы подключаем к решению задачи целый арсенал средств математического анализа. Обычно говорят, последовательность генерируется, порождается производящей функцией. Важно понимать, что это символьная конструкция, то есть вместо символа z может быть любой объект, для которого определены операции сложения и умножения.

История возникновения производящих функций

Известно, что начало методу производящих функций положил английский математик Абрахам де Муавр, а дальнейшему развитию и продолжению данного метода мы обязаны великому математику, имя которого Леонард Эйлер.

Метод производящих функций

Изучение этого мощного механизма позволяющего решать многие задачи, мы начнём с простенькой задачи: сколькими способами можно расположить в линию чёрные и белые шары, общее количество которых равно n?

Обозначим белый шар символом ○, чёрный — ●, T_n — искомое количество расположений шаров. Символом Ø — обозначим нулевое количество шаров. Как и любое решение комбинаторной задачи начнём с тривиальных случаев:

Если n=1, то очевидно имеется 2 способа — взять либо белый шар ○, либо взять чёрный шар ●, таким образом, T₂ = 2.

Если n=2, то имеется 4 способа расположений: ○○, ○●, ●○, ●●.

Рассмотрим случай для n=3. Мы можем начать белым шаром и продолжить 4-мя комбинациями, описанными выше ○○○, ○○●, ○●○, ○●●, или же мы можем начать чёрным шаром и аналогично продолжить 4-мя шарами ●○○, ●○●, ●●○, ●●●.

В итоге количество шаров удвоилось, то есть T₃ = 2T₂. Аналогично T₄ = 2T₃, то есть, обобщая для всех n, получаем рекуррентное уравнение T_n = 2T_n-1 которое и является решением для данной задачи. Решение такого уравнения можно легко угадать — T_n = 2 n (так как 2⋅2 n-1 = 2 n ).

А что если у нас плохо с угадыванием? И что делать, если уравнение будет сложнее? А вообще причём здесь производящие функции?

«Просуммируем» все возможные комбинации расположений шаров:

Вопрос о допустимости такой нелепой на первый взгляд суммы опустим. Будем складывать и умножать последовательности шаров. Со сложением всё понятно, но что значит умножить одну последовательность шаров на другую? Перемножив ○● на ●○ мы получим не что иное как ○●●○. Заметим, однако, что произведение шаров в отличие от произведения чисел не является коммутативным, так как ○●⋅●○ ≠ ●○⋅○●. Символ Ø — в произведении играет роль мультипликативной единицы, то есть Ø ⋅ ○○● = ○○● ⋅ Ø = ○○● и коммутирует с любой последовательностью шаров.

Производя с рядом G последовательность манипуляций, а именно вынося за скобки левый белый и чёрный шары

получим уравнение G = Ø + ○G +●G.

Несмотря на то, что умножение некоммутативно, и мы фактически не различаем левое и правое деление, попробуем всё же «решить» это уравнение, на свой страх и риск. Получим,

Учитывая формулу суммы геометрической прогрессии , имеем

.

В этой сумме так же учтены все возможные варианты разбиения в точности по одному разу. Далее воспользуемся формулой бинома Ньютона: , где — число сочетаний из n по k. Тогда с учетом этого имеем:

Коэффициент при ○ k ● n-k равный числу сочетаний из n по k, показывает общее количество последовательностей из n шаров содержащих ○ шары в количеств k штук и ● шары в количестве n-k штук. Таким образом, общее количество расположений n шаров есть сумма по всем возможным значениям k. Как известно .

Обсуждение метода

Так что же позволяет данному методу быть работоспособным при решении различных задач?

Алгоритм решения задачи можно описать примерно следующим образом: рассматривается некоторая бесконечная сумма, которая в конечном итоге представляет собой формальный степенной ряд G(z) = g₀ + g₁z + g₂z 2 +… + g_nz n +… причем коэффициенты g_k (не заданные в явном виде) — являются ключом к решению исходной задачи. То, что ряд является формальным, говорит о том, что z — является просто символом, то есть вместо него может быть любой объект: число, шар, кость домино и т.д. В отличие от степенных рядов в анализе формальным степенным рядам не придается числовых значений и, соответственно, нет смысла говорить о сходимости таких рядов для числовых аргументов.

Затем производя различные преобразования с бесконечной суммой G(z) мы преобразуем её к замкнутому (компактному) виду. То есть у производящей функции есть 2 представления: бесконечное и замкнутое и, как правило, для решения задачи необходимо бесконечный вид преобразовать к замкнутому, а затем замкнутый вид разложить в степенной ряд, и тем самым получить значения для коэффициентов g_k.

А теперь вооружившись знаниями, вернемся к задаче, которую решал Эйлер.

Я не знаю, как долго Эйлер придумывал решение для этой задачи, но оно поражает своей неожиданностью. Посудите сами. Эйлер рассматривает произведение G(z) = (1+z)(1+z 2 )(1+z 4 )… которое после раскрытия скобок представляется в виде бесконечного ряда G(z) = 1 + g₁z + g₂z 2 + g₃z 3 +….

Следующий шаг Эйлера поражает не менее предыдущего. Он умножает обе части равенства на (1-z).

(1-z)G(z) = (1-z)(1+z)(1+z 2 )(1+z 4 )(1+z 8 )…
(1-z)G(z) = (1-z2)(1+z 2 )(1+z 4 )(1+z 8 )…
(1-z)G(z) = (1-z 4 )(1+z 4 )(1+z 8 )…
(1-z)G(z) = 1

С одной стороны G(z) = 1 + g₁z + g₂z 2 + g₃z 3 +… с другой стороны мы только что получили . Последнее равенство есть не что иное, как сумма геометрической прогрессии, которая равна . Сопоставляя эти два равенства, получаем g₁ = g₂ = g₃ =… = 1, то есть любой груз в k грамм можно взвесить гирями в 1, 2, 4, 8,… грамм притом единственным способом.

Решение рекуррентных соотношений

Производящие функции подходят для решения не только комбинаторных задач. Оказывается, с их помощью можно решать рекуррентные соотношения.

Начнем со всеми знакомой последовательностью чисел Фибоначчи. Каждый из нас знает её рекуррентный вид: F₀ = 0, F₁ = 1, F_n = F_n-1 + F_n-2, n ≥ 2. Однако не каждый знает вид этой формулы в замкнутом виде и это не удивительно, ведь она содержит иррациональное число(«золотое сечение») в своём составе.

Просуммируем эти равенства:

Обозначим левую часть

Рассмотрим каждое из слагаемых в правой части:

Имеем следующее уравнение G(z) = z + z G(z) + z 2 G(z) решая которое относительно G(z) находим

— производящая функция для последовательности чисел Фибоначчи.

Разложим её на сумму простейших дробей, для этого найдем корни уравнения . Решая это простое квадратное уравнение, получаем: . Тогда нашу производящую функцию можно разложить следующим образом:

Следующим шагом является нахождение коэффициентов a и b. Для этого умножим дроби на общий знаменатель:

Подставляя в это уравнение значение z = z₁ и z = z₂, находим

Напоследок немного преобразуем выражение для производящей функции

Теперь каждая из дробей представляет собой сумму геометрической прогрессии.

По формуле находим

Но ведь мы искали G(z) в виде . Отсюда делаем вывод, что

Эту формулу можно переписать в другом виде не используя «золотое сечение»:

что достаточно трудно было ожидать, учитывая красивое рекуррентное уравнение.

Давайте запишем общий алгоритм решения рекуррентных уравнений, используя производящие функции. Он записывается в 4 шага:

Прежде чем переходить к следующему примеру, рассмотрим 2 операции, совершаемые над производящими функциями, которые часто оказываются полезными.

Дифференцирование и интегрирование производящих функций

Для производящих функций обычное определение производной можно записать следующим образом.

Пусть G = G(z) – производящая функция. Производной этой функции называется функция . Дифференцирование, очевидно, линейная операция, поэтому для того, чтобы понять, как оно действует на производящих функциях, достаточно посмотреть на его действие, на степенях переменной. Имеем

Тем самым, действие дифференцирования на произвольной производящей функции
G (z) = g₀ + g₁z + g₂z 2 + g₃z 3 +… дает G΄(z) = g₁ + 2g₂z + 3g₃z 2 + 4g₄z 3 +….

Интегралом называется функция

Операция дифференцирования обратна операции интегрирования:

Операция же интегрирования производной приводит к функции с нулевым свободным членом, и поэтому результат, отличается от исходной функции,

Нетрудно заметить, что для функций, представимых в виде степенных рядов, формула для производной соответствует обычной. Формула для интеграла соответствует значению интеграла с переменным верхним пределом

Используя только что полученные знания о дифференцировании и интегрировании производящих функций, попробуем решить следующее рекуррентное уравнение:

Будем следовать вышеописанному алгоритму. Первое условие алгоритма выполнено. Умножим обе части всех равенств на z в соответствующей степени и просуммируем:

z 0 ⋅ g₀ = 1,
z 1 ⋅ g₁ = z,
z n ⋅ g_n = z n ⋅ g_n-1 + 2z n ⋅ g_n-2 + (-1) n ⋅ z n

Левая часть представляет собой производящую функцию в бесконечном виде.

Попытаемся выразить правую часть через G(z). Рассмотрим каждое слагаемое:

Это и есть производящая функция для заданного рекуррентного уравнения. Раскладывая её на простейшие дроби (например, методом неопределенных коэффициентов или методом подстановки различных значений z), получаем:

Второе и третье слагаемые легко раскладываются в степенной ряд, а вот с первым придется чуть повозиться. Используя правило дифференцирования производящих функций имеем:

Собственно всё. Раскладываем каждое слагаемое в степенной ряд и получаем ответ:

С одной стороны мы искали G(z) в виде , с другой стороны .

Значит, .

Вместо заключения

Возводя в квадрат обе части этого равенства получим

Приравнивая коэффициенты при x n в левой и правой частях, получаем

Эта формула имеет прозрачный комбинаторный смысл, но доказать её непросто. Еще в 80-е годы XX века появились публикации, посвященный этому вопросу.

Источник