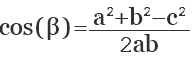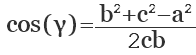Как рассчитать угол треугольника

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

.

.

, .

И, наконец, находим угол C:

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

.

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:

.

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

, .

, .

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Источник

Углы треугольника

Геометрическая фигура из трех отрезков, соединенных между собой тремя точками, не лежащими на одной прямой, называется треугольником. Это — многоугольник с тремя углами. Сумма всех углов треугольника равна 180°. Если известна величина двух из них, третий угол определяем вычитанием из 180° величины двух известных углов.

α = 180°-β-γ

Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.

a 2 = b 2 + c 2 + 2abc cos (α)

Отсюда, косинус искомого угла равняется сумме квадратов смежных сторон (b, с) минус квадрат третей стороны треугольника (а), противолежащей искомому углу, и все это делится на удвоенное произведение смежных сторон:

cos (α) = (b 2 + c 2 — a 2 ) / 2bc

,
где а, b, с — стороны треугольника.
Используя теорему косинусов, определяем косинусы остальных углов. Величины углов в градусах находим по тригонометрической таблице.

Источник

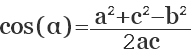
Он-лайн расчет треугольника

Он-лайн калькулятор плоских треугольников. Расчет треугольника по трем сторонам, двум сторонам и углу между, а так же двум углам и прилегающей к ним стороне.
Для начала выберете требующийся вам метод расчета треугольника нажав на одну из трех кнопок. Далее справа, в зависимости от метода расчета, введите длины сторон и величину углов. После следует нажать на кнопку “Рассчитать”.

Если вы заметили ошибку или у вас есть предложения по улучшению работы калькулятора расчета треугольника сообщите нам, пожалуйста, об этом. Написать можно прямо на этой странице ниже в комментариях или воспользовавшись формой контакты

В градусах 60минут. А у вашего сайты в градусе 100 минут.( считает минуты до ста и прибавляет градус). Могут быть большие погрешности. Исправьте пожалуйста

спасибо…
подумаем, как исправить 🙂

как скачать именно такой калькулятор для расчета треугольника спасибо отлично

боюсь, что никак
калькулятор работает только на сайте

Можно на телефоне воспользоватся функцией на телефоне в гугле “Добавить на главный экран” и у вас в понели телефона появится ярлык – ссылка, и вас будет перекижывать на этот сайт;) удачи!

Это десятичные градусы, после точки идут не минуты, а десятые градуса, так что всё правильно. Для расчёта здесь нужно перевести минуты в градусы, поделив на 60, и прибавить полученное к числу градусов, например, 60°30′ = 60,5°

Большое Человеческое Спасибо.

после запятой не минуты а сотые доли градуса, 60 умножте на то что после запятой и получите минуты.

Часто пользовался. Перестал работать… 🙁

спасибо что подсказали! сейчас должно работать..

В треугольнике только первый угол определяет по времени начертания и только одну сторону с ее углами. Сторона не определяют размеров углов /Шпаков А.А. Начальная методология. М., 458 с., 3013 г./..

На практике, нужно учитывать еще и толщину материала. К примеру, треугольник из рейки толщиной 30.
Цены бы небыло такой проге. 🙂

А как рассчитать длину катетов, в равнобедренном прямоугольном треугольнике, по длине гипотенузы?

площадь прямоугольного треугольника равна 64см2,найти его катеты если один из них в 2 раза больше другого

А как насчёт тройки a, b и альфа?

Спасибо огромное!! Очень помогли в работе. Удобный и понятный интерфейс

А где найти алгоритм для решения более сложной задачи- решить треугольник по углу пересечения биссектрис

Можно ли рассчитать треугольник с точностью хотя бы до тысячных. Решение с большими цифрами приводит к очень большой погрешности. Даже сумма углов треугольника не получается 180.

Не работает. При нажатии на кнопку “Рассчитать” просто ничего не происходит. “Опера”.

Да вроде работает.. и в опере..

Чет не работает. Никакой реакции на кнопку “Рассчитать” в режиме “2 угла(по 80*)+сторона(60)”

у меня работает.. все норм..

Большое спасибо за сайт! Очень помогает.
а как рассчитать углы в неправильном шестиугольнике по сторонам?
пробовала разбить его на треугольники, но получается известны только 2 стороны.
Спасибо.

Помогите расчитать объем бетона в кубах. длина 36.200мм ширина 8.800мм толщина по ширине с отметки А 150мм идет до отметки Б 60мм.

Здравствуйте! А можно сделать точность указание углов до тысячной доли?
Мне необходимо рассчитать секунды!

Спасибо большое! Економия времени и труда

И все таки в Опере не работает…

Спасибо! Не думал что так просто все можно подсчитать!

для прямоугольного треугольника калькулятор не работает. Проверяю стороны по теореме Пифагора расхождение сумм квадратов катетов и квадрата гипотенузы более чем в два раза!

У меня все нормально считает. В треугольнике прямой угол есть?

Делаю лестницы. Размеры 3-5-7 метров. Очень удобно считать наклон размеры стутенек. И изменять какие-то размеры без всяких заморочек. Спасибо

Спасибо, очень помогли.

помогите рассчитать гипотенузу в прямоугольном треугольнике, если угол А равен 10 градусам, а основание (прилегающий катет в) равно 12 метрам

не понимаю ничего…..прямоугольный треугольник один катет есть, угол есть какой длины другорй катет. помогите

Не самый лучший калькулятор.

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение треугольников.

Решением треугольника называется нахождение всех его шести элементов (т.е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.

Эта математическая программа находит сторону \( c \), углы \( \alpha \) и \( \beta \) по заданным пользователем сторонам \( a, b \) и углу между ними \( \gamma \)

Программа не только даёт ответ задачи, но и отображает процесс нахождения решения.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Введите стороны \( a, b \) и угол между ними \( \gamma \) Решить треугольник

Источник

Две стороны и угол треугольника

Свойства

Зная две стороны в треугольнике и угол между ними, можно с помощью теоремы косинусов вычислить третью сторону треугольника. Для этого нужно извлечь квадратный корень из суммы квадратов известных сторон и разности с их удвоенным произведением на косинус угла между ними. (рис.76) a^2=b^2+c^2-2bc cos⁡α a=√(b^2+c^2-2bc cos⁡α )

Угол β или γ можно рассчитать через ту же теорему косинусов, зная две, образующие их стороны, при этом один из них – последний, проще найти, отняв два известных от 180 градусов. cos⁡β=(a^2+c^2-b^2)/2ac=(b^2+c^2-2bc cos⁡α+c^2-b^2)/(2c√(b^2+c^2-2bc cos⁡α ))=(2c^2-2bc cos⁡α)/(2c√(b^2+c^2-2bc cos⁡α ))=(c-b cos⁡α)/√(b^2+c^2-2bc cos⁡α ) cos⁡γ=(a^2+b^2-c^2)/2ab=(b^2+c^2-2bc cos⁡α+b^2-c^2)/(2b√(b^2+c^2-2bc cos⁡α ))=(b-c cos⁡α)/√(b^2+c^2-2bc cos⁡α )

Медиана треугольника рассчитывается по вполне однозначной формуле, тогда как если нужно найти медианы через две стороны и угол между ними, то требуются преобразования. m_a=√(2b^2+2c^2-a^2 )/2=√(2b^2+2c^2-b^2-c^2+2bc cos⁡α )/2=√(b^2+c^2+2bc cos⁡α )/2 m_b=√(2a^2+2c^2-b^2 )/2=√(2b^2+2c^2-4bc cos⁡α+2c^2-b^2 )/2=√(b^2+4c^2-4bc cos⁡α )/2 m_c=√(2a^2+2b^2-c^2 )/2=√(2b^2+2c^2-4bc cos⁡α+2b^2-c^2 )/2=√(4b^2+c^2-4bc cos⁡α )/2

Для расчета биссектрис в произвольном треугольнике также существуют стандартные формулы, из которых только одна может быть преобразована и упрощена для двух сторон и угла между ними. l_c=√(ab(a+b+c)(a+b-c))/(a+b) l_b=√(ac(a+b+c)(a+c-b))/(a+c) l_a=√(bc(a+b+c)(b+c-a))/(b+c)=√(bc((b-c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-b^2-c^2+2bc cos⁡α ) )/(b+c)=(bc√(2(1+cos⁡α ) ))/(b+c)

Чтобы найти высоту, нужно знать все три стороны в треугольнике. Подставив их в формулу так, чтобы сторона, на которую опущена искомая высота была в знаменателе, рассчитываются их величины. h_a=(2√(p(p-a)(p-b)(p-c) ))/a h_b=(2√(p(p-a)(p-b)(p-c) ))/b h_c=(2√(p(p-a)(p-b)(p-c) ))/c

Вычислить среднюю линию треугольника можно, зная лишь ту сторону, которой она параллельна, так как сторона будет в два раза больше. В случае с неизвестной стороной, можно подставить в формулу радикал,выведенный по теореме косинусов. M_a=a/2=√(b^2+c^2-2bc cos⁡α )/2 M_b=b/2 M_c=c/2

На пересечении биссектрис в треугольнике расположен центр окружности, которую можно в него вписать. Радиус такой окружности рассчитывается по следующей формуле(рис.75.5) r=√(((p-a)(p-b)(p-c))/p)

Центр описанной вокруг треугольника окружности в свою очередь расположен в точке пересечения медиатрисс, и его формула значительно видоизменена в сравнении с радиусом вписанной окружности. (рис.75.6) R=abc/(4√(p(p-a)(p-b)(p-c)))

Источник