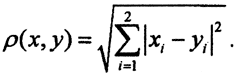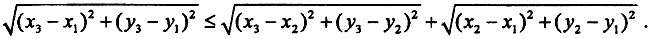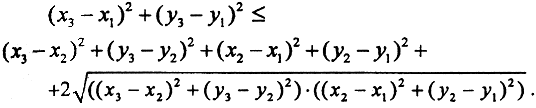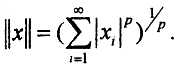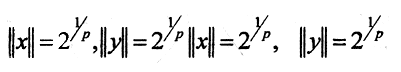доказать что является метрикой

Теория функций действительного переменного/Метрическое пространство

В основе математического анализа лежит понятие предела числовой последовательности и операция предельного перехода. Достаточно сказать, что производная и определённый интеграл определяются через понятие предела. При определении предела используется тот факт, что на числовой прямой определено расстояние между вещественными числами. Но оказывается, что для формулировки многих фундаментальных понятий и доказательства различных теорем анализа важна не природа действительных чисел, а только само понятие расстояния. Обобщением представления о расстоянии между действительными числами на случай произвольного множества является понятие метрики, которое мы сейчас введём.

Содержание

Определение метрического пространства [ править ]

Пусть M — некоторое непустое множество, ρ — некое отображение, ставящие в соответствие двум элементам множества M некоторое вещественное число:

отображение ρ называется метрикой, если оно обладает следующими свойствами (аксиомы метрики):

\rho (x,y)\leq \rho (x,z)+\rho (z,y)>.

Совокупность множества M и определённой на нём метрики ρ называют метрическим пространством и обозначают (M,ρ). Иногда, особенно когда из контекста понятно о какой метрике идёт речь, метрическое пространство обозначают так же, как и само множество М. Элементы метрического пространства обычно называют точками.

Одним из простейших (и важнейших) примеров метрического пространства является числовая прямая. Покажем, что множество вещественных чисел с метрикой ρ(x, y)=|х — у| является метрическим пространством. Действительно, рассмотрим три произвольных вещественных числа

Все аксиомы метрического пространства выполняются, по свойствам модуля:

|x-y|=0\Leftrightarrow x=y> , | x − y | = | − ( y − x ) | = | − 1 | ⋅ | y − x | = | y − x | <\displaystyle

|x-y|=|-(y-x)|=|-1|\cdot |y-x|=|y-x|> , | x − y | = | x − z + z − y | ≤ | x − z | + | z − y | <\displaystyle

|x-y|=|x-z+z-y|\leq |x-z|+|z-y|> .

Пусть (M, ρ) — метрическое пространство, и A — непустое подмножество множества M, тогда (A, ρ) — тоже является метрическим пространством, которое называется подпространством метрического пространства (M,ρ).

Например, множество рациональных чисел является подмножеством действительных чисел:

а следовательно, если взять естественную для вещественных чисел метрику

будет метрическим пространством.

В принципе, любое множество можно рассматривать как метрическое пространство. Действительно, если для элементов произвольного множества ввести так называемую дискретную метрику:

то получится метрическое пространство, которое называют пространством изолированных точек.

На одном и том же множестве можно задавать различные метрики (ниже дан пример), однако не следует считать, что метрику можно задавать произвольно. Дело в том, что при решении практических задач метрика, как правило, является частью постановки задачи.

Свойства метрики [ править ]

Рассмотрим некоторые свойства метрики, которые могут быть выведены из её определения.

Свойство 1. Метрика является неотрицательной функцией:

По аксиоме тождества

\forall x\in M:\rho (x,x)=0> .

С другой стороны, по аксиоме треугольника:

\forall y\in M:\rho (x,x)\leq \rho (x,y)+\rho (y,x)> .

В силу аксиомы симметрии:

\rho (x,y)=\rho (y,x)> ,

Откуда и получается, что

Свойство 2 (Неравенство многоугольника). Для любой конечной системы элементов

множества M имеет место неравенство

Доказательство проводится с помощью метода математической индукции, база индукции — аксиома треугольника.

Но по предположению:

Свойство 3 (Неравенство четырёхугольника). Для любых четырёх элементов

имеет место неравенство

Сравнивая два эти неравенства, получим

Свойство 3а (Второе неравенство треугольника). Для любых трёх элементов

имеет место неравенство

Важные неравенства [ править ]

Для проверки аксиомы треугольника для различных пространств полезны следующие леммы.

Лемма 1 (неравенство Коши-Буняковского):

| ∑ i = 1 n a i b i | ≤ ∑ i = 1 n a i 2 ⋅ ∑ i = 1 n b i 2 <\displaystyle \left|\sum _^a_b_\right|\leq <\sqrt <\sum _^a_^<2>>>\cdot <\sqrt <\sum _^b_^<2>>>> .

F ( t ) = ∑ i = 1 n ( a i t + b i ) 2 ≥ 0 <\displaystyle F(t)=\sum _^(a_t+b_)^<2>\geq 0> .

Применим формулу квадрата суммы:

F ( t ) = t 2 ∑ i = 1 n a i 2 + 2 t ∑ i = 1 n a i b i + ∑ i = 1 n b i 2 <\displaystyle F(t)=t^<2>\sum _^a_^<2>+2t\sum _^a_b_+\sum _^b_^<2>> .

Пусть сначала все a i <\displaystyle a_> равны нулю. В этом случае

Теперь будем считать, что

D = 4 ( ∑ i = 1 n a i b i ) 2 − 4 ∑ i = 1 n a i 2 ∑ i = 1 n b i 2 <\displaystyle D=4\left(\sum _^a_b_\right)^<2>-4\sum _^a_^<2>\sum _^b_^<2>> ,

( ∑ i = 1 n a i b i ) 2 − ∑ i = 1 n a i 2 ∑ i = 1 n b i 2 ≤ 0 <\displaystyle \left(\sum _^a_b_\right)^<2>-\sum _^a_^<2>\sum _^b_^<2>\leq 0>

( ∑ i = 1 n a i b i ) 2 ≤ ∑ i = 1 n a i 2 ∑ i = 1 n b i 2 <\displaystyle \left(\sum _^a_b_\right)^<2>\leq \sum _^a_^<2>\sum _^b_^<2>> .

Лемма 2 (неравенство Минковского):

∑ i = 1 n ( a i + b i ) 2 ≤ ∑ i = 1 n a i 2 + ∑ i = 1 n b i 2 <\displaystyle <\sqrt <\sum _^(a_+b_)^<2>>>\leq <\sqrt <\sum _^a_^<2>>>+<\sqrt <\sum _^b_^<2>>>> .

По формуле квадрата суммы и в силу неравенства Коши-Буняковского:

∑ i = 1 n ( a i + b i ) 2 = ∑ i = 1 n a i 2 + 2 ∑ i = 1 n a i b i + ∑ i = 1 n b i 2 ≤ ∑ i = 1 n a i 2 + 2 ∑ i = 1 n a i 2 ⋅ ∑ i = 1 n b i 2 + ∑ i = 1 n b i 2 <\displaystyle \sum _^(a_+b_)^<2>=\sum _^a_^<2>+2\sum _^a_b_+\sum _^b_^<2>\leq \sum _^a_^<2>+2<\sqrt <\sum _^a_^<2>>>\cdot <\sqrt <\sum _^b_^<2>>>+\sum _^b_^<2>> .

Правая часть этого неравенства может быть записана в виде квадрата суммы:

∑ i = 1 n a i 2 + 2 ∑ i = 1 n a i 2 ∑ i = 1 n b i 2 + ∑ i = 1 n b i 2 = ( ∑ i = 1 n a i 2 + ∑ i = 1 n b i 2 ) 2 <\displaystyle \sum _^a_^<2>+2<\sqrt <\sum _^a_^<2>>><\sqrt <\sum _^b_^<2>>>+\sum _^b_^<2>=\left(<\sqrt <\sum _^a_^<2>>>+<\sqrt <\sum _^b_^<2>>>\right)^<2>> .

∑ i = 1 n ( a i + b i ) 2 ≤ ( ∑ i = 1 n a i 2 + ∑ i = 1 n b i 2 ) 2 <\displaystyle \sum _^(a_+b_)^<2>\leq \left(<\sqrt <\sum _^a_^<2>>>+<\sqrt <\sum _^b_^<2>>>\right)^<2>> .

Неравенство Минковского получается после извлечения квадратного корня из правой и левой части данного неравенства.

Лемма 3 (Интегральное неравенство Коши-Буняковского).

∫ a b f ( t ) g ( t ) d t ≤ ∫ a b f 2 ( t ) d t ⋅ ∫ a b g 2 ( t ) d t <\displaystyle \int \limits _^f(t)g(t)dt\leq <\sqrt <\int \limits _^f^<2>(t)dt>>\cdot <\sqrt <\int \limits _^g^<2>(t)dt>>> .

Рассмотрим неотрицательную функцию

F ( λ ) = ∫ a b [ f ( t ) λ + g ( t ) ] 2 d t <\displaystyle F(\lambda )=\int \limits _^[f(t)\lambda +g(t)]^<2>dt> .

По свойствам интеграла и формуле квадрата суммы:

F ( λ ) = λ 2 ∫ a b f 2 ( t ) d t + 2 λ ∫ a b f ( t ) g ( t ) d t + ∫ a b g 2 ( t ) d t <\displaystyle F(\lambda )=\lambda ^<2>\int \limits _^f^<2>(t)dt+2\lambda \int \limits _^f(t)g(t)dt+\int \limits _^g^<2>(t)dt> .

4 ( ∫ a b f ( t ) g ( t ) d t ) 2 − 4 ∫ a b f 2 ( t ) d t ⋅ ∫ a b g 2 ( t ) d t ≤ 0 <\displaystyle 4\left(\int \limits _^f(t)g(t)dt\right)^<2>-4\int \limits _^f^<2>(t)dt\cdot \int \limits _^g^<2>(t)dt\leq 0> ,

откуда и следует утверждение леммы.

Лемма 4 (Интегральное неравенство Минковского).

∫ a b [ f ( t ) + g ( t ) ] 2 d t ≤ ∫ a b f 2 ( t ) d t + ∫ a b g 2 ( t ) d t <\displaystyle <\sqrt <\int \limits _^[f(t)+g(t)]^<2>dt>>\leq <\sqrt <\int \limits _^f^<2>(t)dt>>+<\sqrt <\int \limits _^g^<2>(t)dt>>> .

По свойствам интеграла:

∫ a b [ f ( t ) + g ( t ) ] 2 d t = ∫ a b f 2 ( t ) d t + 2 ∫ a b f ( t ) g ( t ) d t + ∫ a b g 2 ( t ) d t <\displaystyle \int \limits _^[f(t)+g(t)]^<2>dt=\int \limits _^f^<2>(t)dt+2\int \limits _^f(t)g(t)dt+\int \limits _^g^<2>(t)dt>

Воспользуемся интегральным неравенством Коши-Буняковского:

∫ a b [ f ( t ) + g ( t ) ] 2 d t ≤ ∫ a b f 2 ( t ) d t + 2 ∫ a b f 2 ( t ) d t ⋅ ∫ a b g 2 ( t ) d t + ∫ a b g 2 ( t ) d t <\displaystyle \int \limits _^[f(t)+g(t)]^<2>dt\leq \int \limits _^f^<2>(t)dt+2<\sqrt <\int \limits _^f^<2>(t)dt>>\cdot <\sqrt <\int \limits _^g^<2>(t)dt>>+\int \limits _^g^<2>(t)dt> ,

∫ a b [ f ( t ) + g ( t ) ] 2 d t ≤ ( ∫ a b f 2 ( t ) d t + ∫ a b g 2 ( t ) d t ) 2 <\displaystyle \int \limits _^[f(t)+g(t)]^<2>dt\leq \left(<\sqrt <\int \limits _^f^<2>(t)dt>>+<\sqrt <\int \limits _^g^<2>(t)dt>>\right)^<2>> .

Интегральное неравенство Минковского получается после извлечения квадратного корня из правой и левой части данного неравенства.

Примеры метрических пространств [ править ]

Мы уже рассмотрели два метрических пространства: множество вещественных чисел и множество рациональных чисел. Ниже приведены ещё некоторые примеры метрических пространств, все они играют важную роль в математическом анализе и алгебре.

Проверка первых двух аксиом является, как правило, тривиальной задачей, основные трудности связаны с доказательством справедливости аксиомы треугольника.

Арифметическое евклидово пространство [ править ]

является метрическим пространством.

Перейдём к проверке третьей аксиомы.
3.

По неравенству Минковского (Лемма 2):

то есть аксиома действительно выполняется.

Метрика Хэмминга [ править ]

Метрика такого вида называется метрикой Хэмминга.

Равномерная метрика [ править ]

Таким образом, три рассмотренных примера показывают, что на основе одного и того же множество можно, задавая различные метрики, строить различные метрические пространства.

Комплексные числа [ править ]

является метрическим пространством. Справедливость аксиом следует из свойств модуля комплексного числа. Действительно, если z 1 = x 1 + i y 1 <\displaystyle z_<1>=x_<1>+iy_<1>> , а z 2 = x 2 + i y 2 <\displaystyle z_<2>=x_<2>+iy_<2>> , то

| z 1 − z 2 | = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 <\displaystyle |z_<1>-z_<2>|=<\sqrt <(x_<1>-x_<2>)^<2>+(y_<1>-y_<2>)^<2>>>> ,

таким образом, с точки зрения теории метрических пространств, множество комплексных чисел эквивалентно двумерному арифметическому евклидову пространству (геометрическая интерпретация комплексных чисел).

Непрерывные функции [ править ]

является метрическим пространством.

max x ∈ [ a ; b ] | f ( x ) − g ( x ) | = 0 <\displaystyle \max _|f(x)-g(x)|=0> ,

| f ( x ) − g ( x ) | ≤ max x ∈ [ a ; b ] | f ( x ) − g ( x ) | = 0 <\displaystyle |f(x)-g(x)|\leq \max _|f(x)-g(x)|=0> ,

Аксиома симметрии тоже выполняется.

Докажем теперь аксиому треугольника. Для любых трёх функций

в силу неравенства треугольника для модуля, выполняется неравенство

Возьмём максимальное значение левой и правой части:

max x ∈ [ a ; b ] | f ( x ) − g ( x ) | ≤ max x ∈ [ a ; b ] < | f ( x ) − h ( x ) | + | g ( x ) − h ( x ) | ><\displaystyle \max _|f(x)-g(x)|\leq \max _\left\<|f(x)-h(x)|+|g(x)-h(x)|\right\>> .

w 1 ( x ) + w 2 ( x ) ≤ max x ∈ [ a ; b ] w 1 ( x ) + max x ∈ [ a ; b ] w 2 ( x ) <\displaystyle w_<1>(x)+w_<2>(x)\leq \max _w_<1>(x)+\max _w_<2>(x)> ,

max x ∈ [ a ; b ] < w 1 ( x ) + w 2 ( x ) >≤ max x ∈ [ a ; b ] w 1 ( x ) + max x ∈ [ a ; b ] w 2 ( x ) <\displaystyle \max _\(x)+w_<2>(x)\>\leq \max _w_<1>(x)+\max _w_<2>(x)> ,

то есть наибольшее значение суммы функций не превосходит суммы их наибольших значений.

Используем последнее неравенство, положив

w_<2>(x)=|h(x)-g(x)|> ,

max x ∈ [ a ; b ] < | f ( x ) − h ( x ) | + | h ( x ) − g ( x ) | >≤ max x ∈ [ a ; b ] | f ( x ) − h ( x ) | + max x ∈ [ a ; b ] | h ( x ) − g ( x ) | <\displaystyle \max _\<<|f(x)-h(x)|+|h(x)-g(x)|>\>\leq \max _|f(x)-h(x)|+\max _|h(x)-g(x)|> .

Все аксиомы действительно выполняются.

На множестве непрерывных функций метрику можно определить иначе, например

полученное метрическое пространство обозначают C 2 [ a ; b ] <\displaystyle C_<2>[a;b]> .

Пространства числовых последовательностей [ править ]

Рассмотрим множество всевозможных числовых последовательностей вида

Если на этом множестве ввести расстояние

то получим метрическое пространство, которое обозначают l 2 <\displaystyle l_<2>> . Ряд

∑ k = 1 ∞ ( x k − y k ) 2 <\displaystyle \sum _^<\infty >(x_-y_)^<2>>

сходится, если сходятся ряды

\sum _^<\infty >y_^<2>> ,

а значит введённая метрика имеет смысл для любых последовательностей из l 2 <\displaystyle l_<2>> .

Доказательство аксиом тождества и симметрии не представляет труда, доказательство справедливости аксиомы треугольника для указанной метрики можно с помощью предельного перехода в неравенстве Минковского.

Выводы [ править ]

Приведённые примеры показывают, что понятия метрики и метрического пространства позволяют рассматривать с единых позиций такие непохожие на первый взгляд объекты, как вещественные и комплексные числа, вектора, непрерывные функции и числовые последовательности.

Источник

Доказать что является метрикой

1.4.3. Стандартные метрические пространства

Пример 1. На плоскости R 2 для точек A(x₁, y₁) и B(x₂, y₂) определим расстояние тремя различными способами и покажем, что введенные расстояния являются метриками, то есть проверим выполнимость аксиом.

1.Метрика 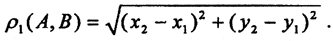. Это евклидова метрика при p = 2

Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки A(x₁, y₁), B(x₂, y₂) и C(x₃, y₃) докажем следующее неравенство:

Возведем это неравенство в квадрат:

Так как (x₃-x₁) 2 ≤(x₃-x₂) 2 +(x₂-x₁) 2 и (y₃-y₁) 2 ≤(y₃-y₂) 2 +(y₂-y₁) 2 (поскольку (b-a) 2 )≤b 2 +a 2 ) и выражение 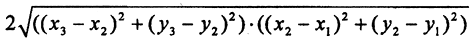неотрицательно, то неравенство является верным.

2. Метрика ρ₂(A,B) = max<|y₂-y₁|, |x₂-x₁|>. Это двумерное арифметическое пространство с супремальной метрикой. Первые аксиомы очевидны. Проверим третью аксиому.

( Комментарий. 1. Понятие пополнения употреблено впрок и будет определено позднее.

2. Любое нормированное пространство является метрическим с метрикой ρ = ||x-y||. Выполнение первых аксиом очевидно. Третья выполняется в силу ||x-y||=||(x-z)+(z-y)||≤||x-z||+||z-y||. Обратное, вообще говоря, неверно, то есть метрические пространства, вообще говоря, не являются нормированными. Но если потребовать, чтобы метрическое пространство обладало инвариантностью относительно сдвигов, то есть ρ(x+z,y+z) = ρ(x,y) и однородностью относительно растяжений, то есть ρ(αx,αy) = |α|ρ(x,y), то тогда верно и обратное, и норма элемента есть метрика, второй элемент которой есть ноль.

Для стандартных метрических пространств это так, так что все вышеприведённые примеры являются одновременно и примерами стандартных норм с геометрией, отличной от эвклидовой. Единичные шары в этих метриках изображены в примере 3.)

Пример 2. Покажем, что ρ = arctg|x-y| является метрикой. Выполнение первых двух аксиом метрики очевидно. Чтобы проверить третью, то есть arctg|x-z+z-y|≤arctg|x-z|+arctg|z-y|, докажем, что для любых α,β ≥0имеет место неравенство arctg(α+β)≤arctgα+arctgβ.

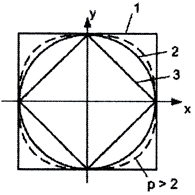
Пример 3. Рассмотрим пространство R 2 _p. Положив y = 0, а ρ = 1, мы получим единичную сферу в пространстве R 2 _p.

При p = 1 уравнение этой сферы имеет вид ||x||₁ = |x|+|y| = 1, и такая метрика называется октаэдрической, потому что единичной сферой в трёхмерном случае ||x||₁ = |x|+|y|+|z| = 1 будет октаэдр.

При p = 2 уравнение этой сферы имеет вид 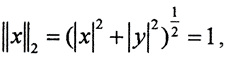и такая метрика называется евклидовой (сферической), потому что единичной сферой в трёхмерном случае будет обычная сфера.

Чебышёвская (кубическая) метрика: ||x||_∞ = max<|x|,|y|>, потому что единичной сферой в трёхмерном случае ||x||_∞ = max <|x|,|y|,|z|>= 1 будет куб.

Пусть неверно, что ρ(x,y)≤ρ(x,z)+ρ(z,y). Тогда ρ(x,y) = 1.⇒x ≠y. Но тогда ρ(x,z)+ρ(z,y) = 0, то есть x=y.

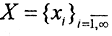
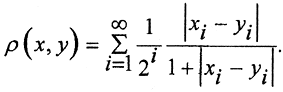
2. Ограниченные последовательности с метрикой Проверим третью аксиому.

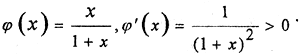
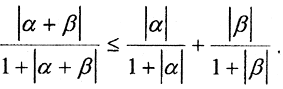
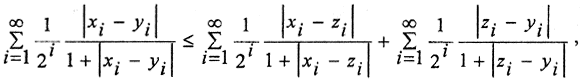
Рассмотрим возрастающую функцию Так как |α+β|≤|α|+|β|, то φ(|α+β|)≤φ(|α|)+φ(|β|), то есть Пусть α = x_i-z_i, β = z_i-y_i, тогда α+β = x_i-y_i. Теперь или ρ(x,y)≤ρ(x,z)+ρ(z,y).

В этой метрике при m ρ(m, n₂) то есть натуральные числа, чем дальше они расположены на числовой оси, тем ближе по метрике ρ.

Ясно, что равенство параллелограмма не выполнено при p≠2.

5. Покажем, что пространство C[0,1] не гильбертово.

Пространство C[0,1] полное нормированное пространство, то есть банахово. (Полноту покажем в следующем пункте.) Уже отмечалось, что норма порождается скалярным произведением, если и только если выполняется равенство параллелограмма ||x+y|| 2 +||x-y|| 2 = 2(||x|| 2 +||y|| 2 ). Пусть x(t) = 1, y(t) = t. Тогда, вычисляя норму в пространстве C[0,1], сразу получим ||t+1|| 2 +||t-1|| 2 = 2 2 +1 2 ≠2(1 2 +1 2 ).

6. Будет ли нормированным пространством линейное пространство непрерывно дифференцируемых функций, если на нём в качестве нормы использовать норму пространства непрерывных функций C[0,1]?

Да. Проверим аксиоматику:

3)||x(t)+y(t)||_t∈[a,b] = max_t∈[a,b]|x(t)+y(t)|≤ max_t∈[a,b](|x(t)|+|y(t)|)≤ max_t∈[a,b]|x(t)|+max_t∈[a,b]|y(t)| = ||x(t)||_t∈[a,b]+||y(t)||_t∈[a,b].

7. Будет ли нормированным пространством линейное пространство непрерывно дифференцируемых функций, если на нём в качестве нормы использовать норму ||x(t)||_t∈[a,b] = max_t∈[a,b]|x'(t)|?

8. Доказать, что подпространство B₁ банахова пространства B является банаховым пространством.

Источник