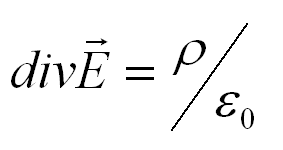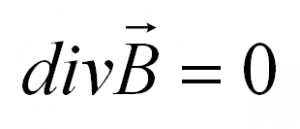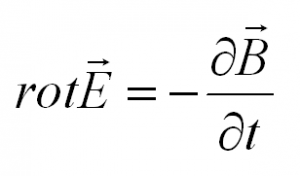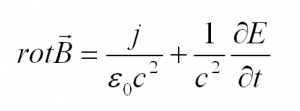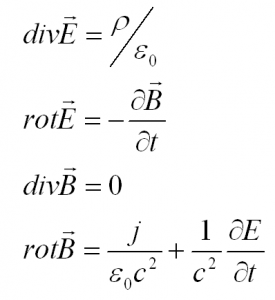уравнения максвелла в ковариантной форме

Система уравнений Максвелла для электромагнитного поля: смысл, способы решения

Уравнения Максвелла в электродинамике – это как законы Ньютона в классической механике или как постулаты Эйнштейна в теории относительности. Фундаментальные уравнения, в сущности которых мы сегодня будем разбираться, чтобы не впадать в ступор от одного их упоминания.

Полезная и интересная информация по другим темам – у нас в телеграм.

Уравнения Максвелла – это система уравнений в дифференциальной или интегральной форме, описывающая любые электромагнитные поля, связь между токами и электрическими зарядами в любых средах.

Уравнения Максвелла неохотно принимались и критически воспринимались учеными-современниками Максвелла. Все потому, что эти уравнения не были похожи ни на что из известного людям ранее.

Тем не менее, и по сей день нет никаких сомнений в правильности уравнений Максвелла, они «работают» не только в привычном нам макромире, но и в области квантовой механики.

Уравнения Максвелла совершили настоящий переворот в восприятии людьми научной картины мира. Так, они предвосхитили открытие радиоволн и показали, что свет имеет электромагнитную природу.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

По порядку запишем и поясним все 4 уравнения. Сразу уточним, что записывать их будем в системе СИ.

Первое уравнение Максвелла

Современный вид первого уравнения Максвелла таков:

Тут нужно пояснить, что такое дивергенция. Дивергенция – это дифференциальный оператор, определяющий поток какого-то поля через определенную поверхность. Уместным будет сравнение с краном или с трубой. Например, чем больше диаметр носика крана и напор в трубе, тем большим будет поток воды через поверхность, которую представляет собой носик.

В первом уравнении Максвелла E – это векторное электрическое поле, а греческая буква «ро» – суммарный заряд, заключенный внутри замкнутой поверхности.

Так вот, поток электрического поля E через любую замкнутую поверхность зависит от суммарного заряда внутри этой поверхности. Данное уравнение представляет собой закон (теорему) Гаусса.

Третье уравнение Максвелла

Сейчас мы пропустим второе уравнение, так как третье уравнение Максвелла – это тоже закон Гаусса, только уже не для электрического поля, но для магнитного.

Что это значит? Поток магнитного поля через замкнутую поверхность равен нулю. Если электрические заряды (положительные и отрицательные) вполне могут существовать по отдельности, порождая вокруг себя электрическое поле, то магнитных зарядов в природе просто не существует.

Второе уравнение Максвелла

Второе уравнение Максвелла представляет собой ни что иное, как закон Фарадея. Его вид:

Ротор электрического поля (интеграл через замкнутую поверхность) равен скорости изменения магнитного потока, пронизывающего эту поверхность. Чтобы лучше понять, возьмем воду в ванной, которая сливается через отверстие. Вокруг отверстия образуется воронка. Ротор – это сумма (интеграл) векторов скоростей частиц воды, которые вращаются вокруг отверстия.

Как Вы помните, на основе закона Фарадея работают электродвигатели: вращающийся магнит порождает ток в катушке.

Четвертое уравнение Максвелла

Это уравнение еще называется теоремой о циркуляции вектора магнитной индукции. Оно говорит нам о том, что электрический ток и изменение электрического поля порождают вихревое магнитное поле.

Приведем теперь всю систему уравнений и кратко обозначим суть каждого из них:

Первое уравнение: электрический заряд порождает электрическое поле

Второе уравнение: изменяющееся магнитное поле порождает вихревое электрическое поле

Третье уравнение: магнитных зарядов не существует

Четвертое уравнение: электрический ток и изменение электрической индукции порождают вихревое магнитное поле

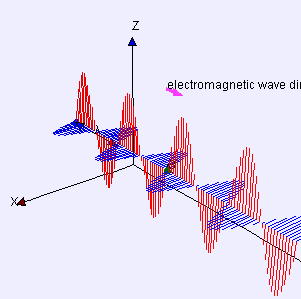
Решая уравнения Максвелла для свободной электромагнитной волны, мы получим следующую картину ее распространения в пространстве:

Надеемся, эта статья поможет систематизировать знания об уравнениях Максвелла. А если понадобиться решить задачу по электродинамике с применением этих уравнений, можете смело обратиться за помощью в студенческий сервис. Подробное объяснение любого задания и отличная оценка гарантированы.

Источник

2 Электромагнитное взаимодействие. Фотон (гамма-квант). Квантовая электродинамика (кэд). Уравнения Максвелла в ковариантной форме Четыре вида взаимодействия элементарных частиц

Главная > Документ

2. ЧАСТИЦЫ И ВЗАИМОДЕЙСТВИЯ 2.3. Электромагнитное взаимодействие

2.3. Электромагнитное взаимодействие

2.3.1. Электромагнитное взаимодействие. Фотон (гамма-квант). Квантовая электродинамика (КЭД). Уравнения Максвелла в ковариантной форме

Четыре вида взаимодействия элементарных частиц

Взаимодействие в физике – это воздействие частиц друг на друга, приводящее к изменению их состояния. Взаимодействие осуществляется посредством тех или иных полей. Согласно квантовой теории поля (КТП) любое поле представляет собой совокупность частиц – квантов этого поля. В природе существует только четыре вида взаимодействия или четыре базовых квантовых поля – сильное, электромагнитное, слабое и гравитационное. Интенсивность каждого взаимодействия определяется своей константой связи альфа, равной квадрату заряда, деленному на четыре пи ().

Электромагнитное взаимодействие – взаимодействие электрических зарядов с электромагнитным полем. Сила электромагнитного взаимодействия между покоящимися элементарными частицами дальнодействующая и изменяется с расстоянием как 1/ r 2 (закон Кулона). Интенсивность электромагнитных процессов в микромире определяется безразмерным параметром е 2 / hc = 1/137. Характерные времена радиационных распадов элементарных частиц и возбужденных состояний ядер по каналу электромагнитного взаимодействия составляют

Электромагнитное взаимодействие универсально для различных явлений и процессов, так как зависит только от электрического заряда.

Принцип калибровочной инвариантности электромагнитного взаимодействия состоит в инвариантности наблюдаемых физических величин относительно калибровочных преобразований векторного и скалярного потенциалов.

Квантовая электродинамика (КЭД) – раздел квантовой теории поля, в котором изучают взаимодействие электромагнитного поля с электронно-позитронным полем. Фотонным вакуумом, или вакуумным состоянием электромагнитного поля, называется низшее энергетическое состояние этого поля. При возбуждении фотонного вакуума происходит рождение частицы кванта электромагнитного поля. Квантовая электродинамика описывает сильные и быстроменяющиеся электромагнитные поля и взаимодействия фотонов и лептонов. Уравнения Максвелла описывают слабые, медленно меняющиеся электромагнитные поля.

Уравнения Максвелла в ковариантной форме

Уравнения Максвелла с токами и зарядами имеют вид

Напряженность электрического и индукция магнитного полей выражаются через векторный потенциал и скалярный потенциал

. (2.10)

Оба потенциала можно представить через 4-векторный потенциал электромагнитного поля

(2.11)

Калибровочные преобразования векторного потенциала и скалярного

(2.12)

возьмем в виде калибровки Лоренца

, (2.13)

где – 4-контравариантная производная, – 4-ковариантная производная, – 4 радиус-вектор и .

Если ввести 4-вектор электрического тока и антисимметричный тензор напряженности электромагнитного поля

, (2.14)

то уравнения Максвелла примут вид (по дважды повторяющимся индексам предполагается суммирование).

(2.15)

и уравнение для 4-векторного потенциала станет следующим:

, (2.16)

Если , то

 = 0. (2.17)

В калибровке Лоренца закон сохранения заряда , тогда уравнение для фотонного поля

 (2.18)

, 2.19)

где – 4-вектор поляризации фотона, q – 4-импульс фотона.

Подставляя (2.19) в (2.18), получаем

q = , (2.20)

т.е. при индексе i = 0 масса покоя фотона равна нулю: .

2.3.2. Уравнение Клейна-Гордона. Уравнение Дирака. Уравнения Лагранжа. Лагранжиан квантовой электродинамики

Для свободной частицы в СТО справедливо релятивистское соотношение для энергии – импульса

или (при с =1), (2.21)

Подставляя в (2.21) дифференциальные операторы энергии и импульса и полагая ħ = с = 1, получаем операторное уравнение для волновой функции ψ

, или ( – m 2 )ψ = 0, (2.22)

которое называется уравнение Клейна-Гордона (фактически это релятивистское уранение Шредингера).

Напомним, что нерелятивисткое волновое уравнение Шредингера для свободной частицы

.

, (2.23)

, (2.24)

или с учетом операторов и ,

. (2.25)

Умножая это уравнение слева на , получаем

. (2.26)

Полагая , окончательно получаем ковариантную форму уравнения Дирака

, (2.27)

, , ,

, ,

, . (2.28)

Шпур (сумма диагональных элементов матрицы) нечетного числа –матриц равен нулю.

–матрицы антикоммутативны: , .

Покажите: , , , , , .

Формально из уравнения Клейна–Гордона можно получить уравнение Дирака :

ψ. (2.29)

Уравнение Дирака – релятивистски инвариантное волновое уравнение, описывающее частицы со спином ½ (электроны, мюоны и нейтрино). Предложено Дираком в 1928 г. В действительности уравнение Дирака представляет собой систему из четырех однородных линейных дифференциальных уравнений первого порядка для четырех волновых функций ( i = 1, 2, 3, 4), в совокупности описывающих состояние частицы. Например, нерелятивистское уравнение Шредингера является уравнением для одной волновой функции .

Функция называется спинорной волновой функцией дираковской частицы.

С помощью матриц Дирака система уравнений для свободной частицы записывается в матричном виде

, (2.30)

где , . По дважды повторяющемуся индексу ведется суммирование: , – обратная комптоновская длина волны частицы с массой .

Для матричных элементов волновой функции получаем четыре уравнения:

, (2.31)

Используя представление Паули для гамма-матриц, получаем систему уравнений Дирака:

,

,

,

. (2.32)

Используя оператор 4-импульса , который является генератором трансляций, уравнение Дирака можно переписать в виде

, (2.33)

. (2.34)

Уравнение для определения собственных функций и собственных значений оператора следующее:

, 2.35)

где собственные значения операторов .

Волновая функция свободной частицы с импульсом и энергией Е описывается плоской волной де Бройля:

. (2.36)

С учетом (2.35) и (2.36) уравнение (2.34) может быть переписано в форме

, (2.37)

где , .

При заданном значении импульса существуют решения, соответствующие двум знакам энергии

. (2.38)

Физический смысл существования решений, отвечающих отрицательной энергии, разъясняется существованием частиц и античастиц. Все уровни с Уравнения Лагранжа

Уравнение Лагранжа для частиц, как известно, имеет вид

, где , (2.39)

здесь функция Лагранжа , Функция Гамильтона ,

где Т – кинетическая энергия системы, V – потенциальная энергия.

Для полей =(систем с непрерывно меняющими координатами)

, (2.40)

плотность оператора Лагранжа (Лагранжиан) :

. (2.41)

. (2.42)

Пример1. Лагранжиан при подстановке в уравнение (2.42) дает уравнение Клейна–Гордона:

(– m 2 )φ = 0.

Пример 2. Лагранжиан приводит к уравнению Дирака при подстановке в (2.42). Каждая из четырех компонент волновых функций и рассматривается как независимая переменная.

Пример3. При подстановке лагранжиана в уравнение Эйлера–Лагранжа (2.42) получаются уравнения Максвелла:

,

где , электронный ток .

Пример 4. В случае неабелевых (некоммутативных) калибровочных групп роль электромагнитного поля играют многокомпонентные поля , называемые полями Янга – Миллса.

Уравнения Эйлера – Лагранжа для полей Янга – Миллса имеют вид

, (2.43)

где ковариантная производная

, – ток полей материи,

для группы , где – матрицы Паули.(),

для группы SU(3) , где – матрицы Гелл–Мана (),

тензор напряженности поля Янга – Миллса –

, (2.44)

где – константа взамодействия. Физический смысл – тензор кривизны внутреннего пространства. Само поле Янга-Миллса описывает параллельный перенос в пространстве внутренней симметрии.

Действительное векторное поле описывает нейтральные частицы, комплексное векторное поле – заряженные частицы.

Лагранжиан квантовой электродинамики (КЭД)

При описании свойств и взаимодействий элементарных частиц вводится понятие физического поля, которое ставится в соответствие каждой частице. Физические поля состоят из отдельных порций – квантов. Математический аппарат квантовой теории поля позволяет описать рождение и уничтожение частицы в каждой пространственно-временной точке. Для описания процессов, происходящих с элементарными частицами в квантовой теории поля, используется формализм Лагранжа. В Лагранжиане, построенном из полей, участвующих во взаимодействии частиц, заключены все сведения о свойствах частиц и динамике их поведения. Лагранжиан состоит из лагранжиана, описывающего поведение свободных полей и лагранжиана взаимодействия различных полей.

Лагранжиан (КЭД) представляет собой сумму кинетической энергии частиц электронного поля – первое слагаемое, кинетической энергии фотонного поля – третье слагаемое, и энергии взаимодействия электронного и фотонного полей – второе слагаемое:

, (2.45)

здесь – сопряженный оператор, уничтожает позитрон или рождает электрон в пространственно–временной точке х ;

– оператор, уничтожает электрон или рождает позитрон;

– четыре матрицы Дирака ,,,;

– частная производная по 4-координате ;

– масса частицы(электрона), е – электрический заряд частицы;

– 4-потенциал фотонного поля;

– калибровочно–инвариантный тензор напряженности поля фотонов;

– антисимметричный тензор электромагнитного поля.

Слагаемое в лагранжиане отсутствует, поэтому частица электромагнитного поля – фотон безмассовая ().

Лагранжиан КЭД инвариантен относительно локального (в точке х ) калибровочного преобразования электронного поля

, (2.46)

, (2.47)

– произвольная функция пространственных координат и времени.

. (2.48)

2.3.3. Диаграммы Феймана

Диаграммы Феймана – графический способ описания взаимодействий в квантовой теории поля. Метод предложен Р.Фейманом в 1949 г. для описания амплитуд рассения и взаимного превращения элементарных частиц. Составными элементами диаграмм являются вершины, внутренние и внешние линии. Внутренние линии присоединяются к двум вершинам. Внешняя линия присоединяется к одной вершине. Иногда диаграммы ориентируют относительно времени, направление которого показывают отдельной стрелкой. Диаграммы могут быть достаточно сложными и образовывать бесконечные ряды. Их используют для расчетов по теории возмущений в квантовой теории поля. Мы будем применять диаграммы только для иллюстрации процессов.

Существуют правила построения диаграмм Феймана. Каждому элементу диаграмм сопоставляют определенный математический объект (величину и операцию).

Вершина – элементарный графический символ (точка или кружок), изображает акт локального элементарного взаимодействия квантовых полей, соответствует каждому отдельному превращению частиц. Узел – кружок, изображающий сложный процесс взаимодействия частиц в вершине.

Внутренним линиям соответствует распространение промежуточной виртуальной частицы от одного акта превращения до другого акта превращения.

Внешним линиям соответствуют волновые функции начальных и конечных реальных частиц, участвующих в процессе.

Кварки обозначаютс я толстыми линиями со стрелкой на линии.

Глюоны – плоскими пересекающимися винтовыми линиями.

Вионы обозначают пунктирными линиями.

Барионы изображаютс я тремя кварковыми линиями,

Мезоны – двумя кварковыми линиями.

Античастицы изображаются линиями со стрелками, направление которых противоположно во времени стрелкам частиц.

Следует отметить, что различные авторы используют свои обозначения и общего стандарта начертания диаграмм не существует. Иногда на диаграммах дополнительными стрелками показывают направление импульсов частиц, времени и т.д.

Физический смысл диаграмм Феймана состоит в наглядном представлении реальных реакций, происходящих с элементарными частицами в виде последовательности элементарных виртуальных процессов. В каждом узле феймановской диаграммы сохраняются все законы сохранения зарядов, энергии и импульса и момента импульса. Во внутренних линиях, как правило, имеет место нарушение связи между энергией, массой и импульсом частиц , но закон сохранения энергии выполняется. Такие частицы называются виртуальными и говорят «виртуальные частицы находятся вне массовой поверхности», имея в виду данное неравенство.

В квантовой электродинамике имеется всего одна вершина, одна фотонная линия, одна электронная линия, а также позитронная линия со стрелкой против направления времени (см. рис. 2.8-2.9.)

Рис. 2.8. Вершина в КЭД

а) электронная линия,

б) позитронная линия,

в) фотонная линия,

Рис. 2.9. Линии в КЭД: а) электронная линия, б) позитронная линия, в) фотонная линия

На рис. 2.10, 2.12 приведены феймановские диаграмы комптоновского рассеяния , и мёллеровское рассеяние электронов

Рис. 2.10. Феймановская диаграмма упругого рассеяния гамма-кванта на свободном электроне

Рис. 2.11. Феймановская диаграмма двухфотонной аннигиляции электрона

и позитрона.

Рис.2.12. Мёллеровское рассеяние электронов. . Электрон испускает виртуальный –квант и переходит в состояние . Электрон упруго рассеивается на виртуальном –кванте и переходит в состояние

В заключение отметим, что, хотя квантовая электродинамика описывает электромагнитное взаимодействие только двух частиц электрона и фотона, она является законченной теорией, находится в блестящем согласии с экспериментами и объясняет громадное количество природных явлений. Если «выключить» электромагнитное взаимодействие, то распались бы атомы, молекулы, исчезла бы жизнь, а также исчезли бы силы упругости, силы трения, поверхностного натяжения, химические явления.

Источник