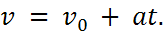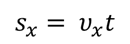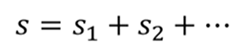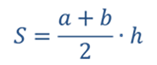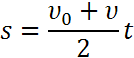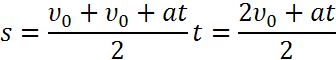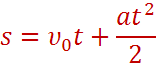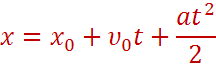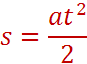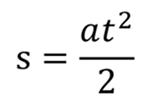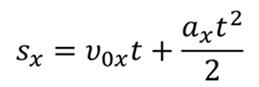уравнение перемещения тела с учетом времени
Перемещение и путь при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.
При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:
Пример №1. По графику определить перемещение тела в момент времени t=3 с.
Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:
Извлекаем из графика необходимые данные:
Подставляем известные данные в формулу:
Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещения
Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
В итоге получается формула:
Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v0 = 0), эта формула принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:
Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.
Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
Когда тело тормозит, через некоторое время t1оно останавливается. Поэтому скорость в момент времени t1 равна 0:
При торможении перемещение s1 равно:
Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
При разгоне перемещение s2 равно:
При этом модуль перемещения в течение всего времени движения равен:
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:
Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
Подставляем выраженные величины в формулу:
Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:
За первую секунду тело переместится на расстояние, равное:
За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:
За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:
Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:
Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду
Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:
Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:
где t — время одного промежутка, а n — порядковый номер этого промежутка.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:
Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:
График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:
Определение направления знака проекции ускорения по графику его перемещения:
Пример №6. Определить ускорение тела по графику его перемещения.
Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:
Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:
График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.
В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:
Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.
При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:
Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Перемещение тела при равноускоренном движении
Урок 5. Физика 9 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Перемещение тела при равноускоренном движении»
Прямолинейным равноускоренным движением называется движение, при котором скорость тела за любые равные промежутки времени изменялась на одинаковую величину. И основной характеристикой такого движения являлось ускорение — это физическая векторная величина, характеризующая быстроту изменения скорости.
Как определить координату тела, пройденный путь и перемещение при прямолинейном равноускоренном движении?
Это можно сделать, если рассмотреть прямолинейное равноускоренное движение как набор большого количества очень малых равномерных перемещений тела.
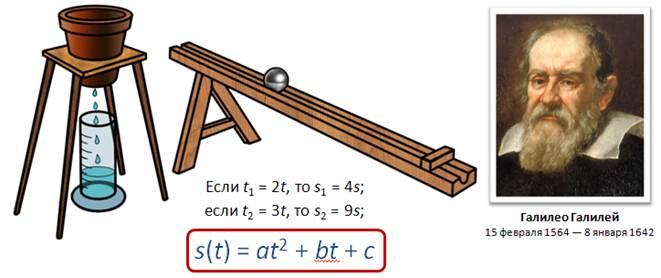
Первым решил задачу местоположения тела в определённый момент времени при ускоренном движении итальянский учёный Галилео Галилей. Галилей использовал наклонную плоскость с гладкой канавкой посередине, по которой скатывались латунные шары. По водным часам он засекал определённый интервал времени и фиксировал расстояния, которые за это время преодолевали шары. Галилей выяснил, что если время увеличить в два раза, то шары прокатятся в четыре раза дальше (т.е. зависимость квадратичная). Это опровергало мнение Аристотеля, что скорость шаров будет постоянной.
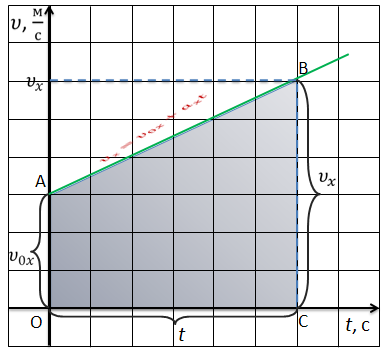
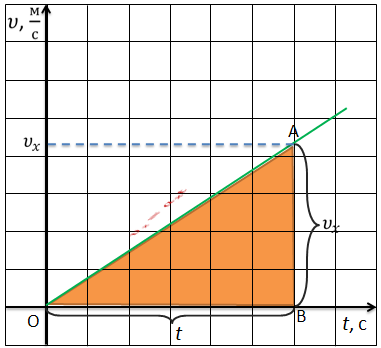
Получим формулу для определения перемещения при равноускоренном движении графическим методом.
Известно, что при равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле
Т. е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой.
Прямая 1 соответствует движению с положительным ускорением (скорость увеличивается), прямая 2 — движению с отрицательным ускорением (скорость убывает).
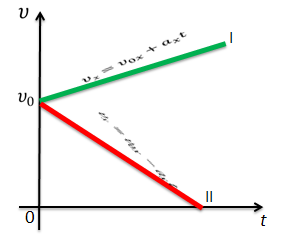
График скорости разобьем на маленькие прямоугольные участки. Каждый участок будет соответствовать определённой постоянной скорости.
Необходимо определить пройденный путь за первый промежуток времени. Запишем формулу
Теперь посчитаем суммарную площадь всех имеющихся у нас фигур. А сумма площадей при равномерном движении – это полный пройденный путь.
Обратите внимание, от точки к точке скорость будет изменяться, тем самым можно получить путь, пройденный телом именно при прямолинейном равноускоренном движении.
Заметим, что при прямолинейном равноускоренном движении тела, когда скорость и ускорение направлены в одну сторону, модуль перемещения равен пройденному пути, поэтому, когда определяется модуль перемещения, то определяется и пройденный путь.
В данном случае можно говорить, что модуль перемещения будет равен площади фигуры, ограниченной графиком скорости и осью времени.
Фигура, ограниченная графиком скорости и осью времени есть не что иное, как прямоугольная трапеция. Из математики известна формула для нахождения площади трапеции. Площадь трапеции равна произведению половины суммы её оснований на высоту.
Следовательно, перемещение за все время tчисленно равно площади трапеции ОАВС. В нашем случае длина одного из оснований численно равна υoх, длина другого — υх. Высота же ее численно равна t. Отсюда следует, что перемещение равно:
Подставим в эту формулу вместо υ равную ей величину υ0 + at.Тогда
Разделив почленно числитель на знаменатель, получим
Это есть уравнение перемещения в проекциях на ось координат.
При пользовании этой формулой нужно помнить, что s, υ0 и а могут быть как положительными, так и отрицательными — ведь это проекции векторов пути, начальной скорости и ускорения на ось X.
Теперь вспомним, что пройденный путь, равный в нашем случае модулю перемещения, выражается разностью: s = x – x0
Если в уравнение подставить полученное нами выражение для S, то запишем закон, по которому движется тело при прямолинейном равноускоренном движении:
Это уравнение называется основным кинематическим уравнением равноускоренного движения.
Если тело движется из состояния покоя, график проходит через начало координат, фигура под графиком – прямоугольный треугольник, площадь которого равна половине произведения катетов.
Тогда формула для определения перемещения принимает вид:
Это уравнение перемещения при равноускоренном движении без начальной скорости.
Рассмотрим некоторые важные зависимости между величинами равноускоренного движения. Для равноускоренного движения без начальной скорости путь, пройденный телом, пропорционален квадрату времени. Значит, пути, пройденные телом за 1 с, 2 с, 3 с, 4 с будут относиться как квадраты последовательных натуральных чисел.
Для любого равноускоренного движения, пути, пройденные телом за любые равные промежутки времени, будут относиться как последовательный ряд нечетных чисел.
– Перемещение тела за все время t численно равно площади трапеции, ограниченной графиком скорости и осью времени.
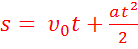
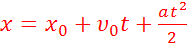
– Для равноускоренного движения без начальной скорости путь, пройденный телом, пропорционален квадрату времени.
– Для любого равноускоренного движения, пути, пройденныетеломза любые равные промежутки времени, будутотноситьсякакпоследовательный ряд нечетных чисел.
Как посчитать путь ускоряющегося тела не используя время
Существует формула, с помощью которой можно посчитать путь, пройденный телом, когда нам известны его начальная скорость, ускорение и конечная скорость.
Сокращенно эту формулу называют «путь без времени». Так ее называют потому, что в правой ее части время t движения отсутствует (рис. 1).
Формула пути без времени помогает упростить решение некоторых задач кинематики. Особенно, задач, части C.
Однако, не торопитесь на ЕГЭ записывать эту формулу в готовом виде. Сначала в решении задачи нужно записать вывод этой формулы. И только потом ее можно использовать.
Формулу выводят из выражений для равнопеременного движения. Сейчас я помогу вам вывести эту формулу с помощью нескольких простых шагов.
Выводим формулу пути без времени
Для определенности будем считать, что тело движется по прямой все быстрее и быстрее. То есть, скорость тела увеличивается, так как появляется ускорение.
В таком случае векторы ускорения и скорости тела будут сонаправленными (параллельными и направленными в одну и ту же сторону).
Сонаправленные или противоположно направленные векторы называют коллинеарными векторами. Прочитайте подробнее о коллинеарных векторах.
Чтобы вычислить путь тела, когда скорость его увеличивается, нужно использовать две формулы:
\( \large v_ <0>\left( \frac<\text<м>>
\( \large v \left( \frac<\text<м>>
\( \large a \left( \frac<\text<м>>
\( \large S \left( \text <м>\right)\) – путь, пройденный телом;
\(\large t \left( c \right)\) – время, за которое тело прошло этот путь.
В формуле для пути S присутствует время t. Получим из нее формулу для пути, в которой время будет отсутствовать.
Что сделать, чтобы получить формулу пути, в которой отсутствует время:
Выражаем время из формулы для скорости
Выпишем формулу, связывающую начальную и конечную скорость тела:
\[ \large v = v_ <0>+ a \cdot t \]
Избавимся в правой части от начальной скорости, обозначенной символом \( v_<0>\). Для этого из обеих частей уравнения вычтем число \( v_<0>\). Получим такую запись:
\[ \large v — v_ <0>= a \cdot t \]
Теперь, чтобы справа в формуле оставалось только время «t», избавимся от ускорения «a». Для этого разделим обе части уравнения на «a»:
Это выражение нам пригодится для дальнейшего вывода формулы «путь без времени».
В формулу пути подставим выражение для времени
Запишем теперь формулу для пути S и полученную формулу для времени t, объединив их в систему:
В первом уравнении системы будем заменять символ t дробью из второго уравнения. Тогда система из двух уравнений превратится в единственное уравнение. И в этом уравнении не будет символа t времени:
Осталось теперь упростить полученное выражение. Будем производить упрощение по частям.
Упрощаем выражение, расположенное до знака «плюс» в правой части
Выпишем отдельно все, что располагается до знака «плюс» в правой части уравнения:
Умножим числитель дроби на число \(v_<0>\).
В числитель дроби, обособленный с помощью скобок помещаем число \(v_<0>\):
Теперь необходимо умножить скобку на число \(v_<0>\). На рисунке 2 указано, как правильно выражение в скобках умножить на число, стоящее за скобками.
Нужно к каждой скорости в скобках дописать число \(v_<0>\), умножая его на эти скорости. Получим такое выражение:
То есть, вместо первоначальной записи, мы получили такую запись:
Возводим в квадрат дробь
После знака «плюс» в правой части уравнения располагается дробь, которую нужно возвести в квадрат. Обратим внимание на эту дробь:
Правильно возвести дробь в степень поможет рисунок 3.
В результате возведения в квадрат дробь приобретет такой вид:
В числителе этой дроби находится выражение в скобках, которое нужно возвести в квадрат. И нам придется применить одну из формул сокращенного умножения. Запоминать формулы сокращенного умножения удобно в виде, приведенном на рисунке 4.
Используем для этого формулу сокращенного умножения, которая содержит знак «минус». Она называется «Квадрат разности». Тогда числитель дроби превратится в такую запись:
Теперь можем записать полученную дробь:
Упрощаем правую часть, записанную после знака «плюс»
Обратим внимание на все, что располагается в правой части уравнения после знака «плюс»:
Мы уже провели некоторые преобразования и можем теперь заменить дробь, возводимую в квадрат более подробной записью:
Примечание: Когда мы умножаем одну дробь на другую, то можем менять местами знаменатели этих дробей.
Итак, поменяем местами знаменатели дробей:
Теперь видно, что мы можем сократить ускорение и еще немного упростить выражение:
А перемножив числители и знаменатели двух дробей, получим такую запись:
Теперь, первоначальную дробь можно заменить дробью, полученной в ходе преобразований:
Мы закончили преобразовывать выражения, содержащиеся в правой части уравнения после знака «плюс».
Теперь, осталось сложить две дроби в правой части – дробь, записанную до знака «плюс» с дробью, записанной после знака «плюс». А чтобы эти дроби можно было сложить, нужно будет привести их к общему знаменателю.
Приводим к общему знаменателю дроби в правой части уравнения
Вернемся еще раз к первоначальному уравнению:
Заменим правую часть этого уравнения выражениями, которые мы получили:
Сравним знаменатели дробей.
Первая дробь обладает знаменателем «a», а вторая – «2a». Выберем число «2a» в качестве общего знаменателя обеих дробей.
Чтобы первую дробь привести к общему знаменателю «2a», умножим ее на единицу:
Примечания:
Так как снизу в первой дроби не хватает числа 2, то единицу представим в виде дроби 2/2:
Получим такую дробь:
Поместим ее в выражение для пути:
Дроби с одинаковыми знаменателями складываем
Теперь знаменатели дробей равны. И мы можем записать эти дроби под общим знаменателем:
Раскроем скобки в числителе полученного выражения:
Примечание: Обратим внимание на то, что в числителе дважды встречается член \(2v_ <0>v\), обладающий различными знаками. В начале числителя – знаком «плюс», а в конце числителя – знаком «минус». Это означает, что из числа \(2v_<0>v\) вычитается такое же число \(2vv_<0>\). В конце концов, это число покидает нашу запись и, она упрощается:
Перепишем выражение, записав все, что содержит знак «плюс» в начало числителя:
Вычтем подобные члены, содержащие \( v^<2>_<0>\):
В результате получим короткую запись. Именно о ней говорят, когда имеется ввиду формула пути без времени:
Примечания:
Как выглядит формула пути без времени, когда скорость тела уменьшается
Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:
Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:
Выводы
Пусть нам известны начальная и конечная скорость тела и его ускорение. Тогда путь, пройденный телом, можно рассчитать так: