уравнение эллипса в параметрической форме
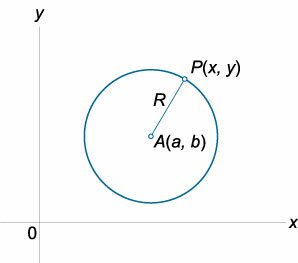
Уравнение эллипса в параметрической форме
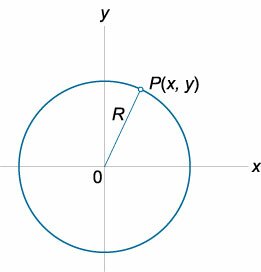
Уравнение окружности в параметрической форме
\( \left\ < \begin
где \(x\), \(y\) − координаты точек окружности, \(R\) − радиус окружности, \(t\) − параметр.
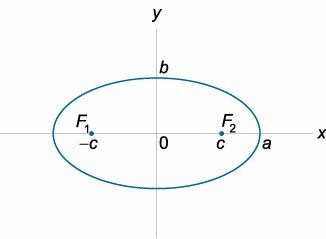
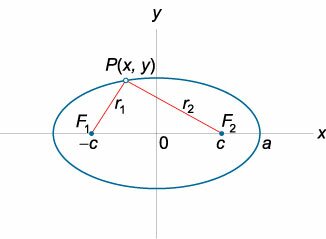
Сумма расстояний от любой точки эллипса до его фокусов постоянна:
\(
где \(
Соотношение между полуосями эллипса и фокусным расстоянием
\(
где \(a\) − большая полуось эллипса, \(b\) − малая полуось, \(c\) − половина фокусного расстояния.
Уравнение эллипса в параметрической форме
\( \left\ < \begin
где \(a\), \(b\) − полуоси эллипса, \(t\) − параметр.
Общее уравнение эллипса
\(A
где \(
\(A
где \(AC > 0\).
Периметр эллипса
\(L = 4aE\left( e \right)\),
где \(a\) − большая полуось эллипса, \(e\) − эксцентриситет, \(E\) − полный эллиптический интеграл второго рода.
Площадь эллипса
\(S = \pi ab\)
Аналитическая геометрия f(x)dx.Ru
Математика, Аналитическая Геометрия
Разделы
Последние
Свойства эллипса. Параметрические уравнения эллипса
п.3. Свойства эллипса.
Теорема. (Свойства эллипса.)
1. В канонической для эллипса системе координат, все
точки эллипса находятся в прямоугольнике


2. Точки 
3. Эллипс является кривой, симметричной относительно
своих главных осей.
4. Центр эллипса является его центром симметрии.
Доказательство. 1, 2) Сразу же следует из канонического уравнения эллипса.
3, 4) Пусть М(х, у) – произвольная точка эллипса. Тогда ее координаты удовлетворяют уравнению (4). Но тогда координаты точек 
Определение. Величина 2а называется большой осью эллипса, величина а называется большой полуосью эллипса.
Определение. Величина 2b называется малой осью эллипса, величина b называется малой полуосью эллипса.
Определение. Точки пересечения эллипса с его главными осями называются вершинами эллипса.
Замечание. Эллипс можно построить следующим образом. На плоскости в фокусы «забиваем по гвоздю» и закрепляем на них нить длиной 
Из определения эксцентриситета следует, что
Зафиксируем число а и устремим число с к нулю. Тогда при 




Таким образом, мы можем считать, что окружность есть эллипс с нулевым эксцентриситетом.
Устремим теперь 



п.4. Параметрические уравнения эллипса.
Теорема. Пусть 


является параметрическими уравнениями эллипса в канонических для эллипса системе координат.
Доказательство. Достаточно доказать, что система уравнений (6) равносильна уравнению (4), т.е. они имеют одно и то же множество решений.
1) Пусть (х, у) – произвольное решение системы (6). Разделим первое уравнение на а, второе – на b, возводим оба уравнения в квадрат и складываем:

Т.е. любое решение (х, у) системы (6) удовлетворяет уравнению (4).
2) Обратно, пусть пара (х, у) является решением уравнения (4), т.е.

Из этого равенства следует, что точка с координатами 

Из определения синуса и косинуса сразу же следует, что



Замечание. Эллипс можно получить в результате равномерного «сжатия» окружности радиуса а к оси абсцисс.
Пусть 



При этом преобразовании каждая точка окружности «переходит» в другую точку плоскости, имеющую ту же самую абсциссу, но меньшую ординату. Выразим старую ординату точки через новую:
и подставим в уравнение окружности:


Отсюда следует, что если до преобразования «сжатия» точка М(х, у) лежала на окружности, т.е. ее координаты удовлетворяли уравнению окружности, то после преображования «сжатия» эта точка «перешла» в точку 

Эллипс
Определение эллипса.
Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
\frac
$$
при условии \(a \geq b > 0\).
Из уравнения \eqref
Рис. 8.1. Эллипс
Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.
Внешний вид эллипса проще всего описать сравнением с окружностью радиуса \(a\) с центром в центре эллипса: \(x^<2>+y^<2>=a^<2>\). При каждом \(x\) таком, что \(|x| Рис. 8.2. Сжатие окружности к эллипсу. Ординаты всех точек уменьшаются в отношении \(b/a\).
Фокусы, эксценриситет и директрисы эллипса.
У эллипса есть две замечательные точки, которые называются его фокусами.
Фокусами называются точки \(F_<1>\) и \(F_<2>\) с координатами \((c, 0)\) и \((-c, 0)\) в канонической системе координат (рис. 8.3).
Рис. 8.3. Фокусы эллипса.
Для окружности \(c=0\), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.
Отметим, что \(\varepsilon Утверждение 2.
Расстояние от произвольной точки \(M(x, y)\), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы \(x\):
$$
r_<1>=|F_<1>M|=a-\varepsilon x,\ r_<2>=|F_<2>M|=a+\varepsilon x.\label
$$
Очевидно, что \(r_<1>^<2>=(x-c)^<2>+y^<2>\). Подставим сюда выражение для \(y^<2>\), найденное из уравнения эллипса. Мы получим
$$
r_<1>^<2>=x^<2>-2cx+c^<2>+b^<2>-\frac
$$
Учитывая равенство \eqref
$$
r_<1>^<2>=a^<2>-2cx+\frac
$$
Так как \(x \leq a\) и \(\varepsilon Утверждение 3.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса \(2a\).
Необходимость. Если мы сложим равенства \eqref
$$
r_<1>+r_<2>=2a.\label
$$
Достаточность. Пусть для точки \(M(x, y)\) выполнено условие \eqref
$$
\sqrt<(x-c)^<2>+y^<2>>=2a-\sqrt<(x+c)^<2>+y^<2>>.\nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^<2>=a\sqrt<(x+c)^<2>+y^<2>>.\label
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение \eqref
Рис. 8.4. Фокусы и директрисы эллипса.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса \(\varepsilon\).
Уравнение касательной к эллипсу.
Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть \(M_<0>(x_<0>, y_<0>)\) — точка на эллипсе и \(y_ <0>\neq 0\). Через \(M_<0>\) проходит график некоторой функции \(y=f(x)\), который целиком лежит на эллипсе. (Для \(y_ <0>> 0\) это график \(f_<1>(x)=b\sqrt<1-x^<2>/a^<2>>\), для \(y_ <0>Утверждение 5.
Касательная к эллипсу в точке \(M_<0>(x_<0>, y_<0>)\) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.
Рис. 8.5.
Координаты точки эллипса по углу
IP76 > Координаты точки эллипса по углу
Для нахождения координат точки эллипса по углу существует простое и элегантное решение. Понимаю, что для маститого математика это решение является очевидным. Однако, для меня в то далекое время, когда инет был диким, связь модемной, а я сильно молодым, это таковым не являлось.
Калькулятор точки на эллипсе
Давайте посмотрим, как это выглядит на практике. Потом теория. Оранжевый маркер отвечает за угол, на основании которого считаем координаты. Красный — параметрический угол, о котором ниже.
Get a better browser, bro…
Параметрическое уравнение эллипса
Обратимся, как обычно, к Википедии. Находим там следующее:
Каноническое уравнение эллипса может быть параметризовано:
Очевидно, что t — это угол, и это не «наш» угол. Это какой-то другой угол, который функционально связан с «нашим». «Нашим» называю угол, от которого требуется посчитать координаты.
Таким образом, задача нахождения координат точки эллипса по углу сводится к задаче нахождения угла t, зависящим от требуемого. Нахождением этой зависимости и займемся.
Подготовка
У нас есть эллипс, описанный двумя полуосями a и b. Представим две окружности, имеющих общий центр. Меньшая окружность (зеленая) имеет радиус b. Большая окружность (синяя) имеет радиус a.
Проведем прямую из общего центра [X0;Y0] в произвольную точку плоскости [X;Y]. В результате пересечения с этими окружностями получаются две точки [X1;Y1] и [X2;Y2].
α – угол между прямой и осью X.
| Малая окружность | X1 = b × cos α | Y1 = b × sin α |
| Большая окружность | X2 = a × cos α | Y2 = a × sin α |
Таблица 1. Координаты точек пересечения прямой с окружностями
Нахождение зависимости
Используя уравнение (1) посчитаем координаты точки на эллипсе [X’;Y’] для угла α. Проведем прямую из центра [X0;Y0] в точку [X’;Y’]. Угол β – угол между этой прямой и осью X.
Задача сводится к тому, чтобы найти такой α, при котором β был бы равен интересующему нас углу. Таким образом, угол α будет являться параметром в уравнении (1) для требуемого угла β.
Найдем зависимость между получившимся углом β и углом α. На рисунке видно, что прилегающий к углу катет (синий) равен ранее рассчитанному X2, а противолежащий (зеленый) равен Y1:
X’ = X2 = a × cos α
Y’ = Y1 = b × sin α
Опыт показывает, что тут зачастую возникает легкий ступор. Возможно, рисунок вводит в некое заблуждение. Видим треугольник, и если с синим катетом вопросов нет, то с зеленым — масса. Почему синус от α? Угол «вона где», тут синус вообще не от того угла и т.д.
Смотрим на пересечение прямой и малой (зеленой) окружности. Зеленый катет прилетает именно оттуда. Именно так координату Y’ и рассчитывали, согласно уравнению(1). Рисунок — это иллюстрация, не метод решения.
Тангенс угла β в этом случае равен:
Используя формулу тангенса произведем дальнейшие преобразования:
(4) Зависимость тангенса α от тангенса β
Таким образом, видим прямую зависимость угла α, который нужен нам в качестве параметра в уравнении(1), от угла β, координаты точки от которого хотим получить.
Нахождение координат
Угол α находим через арктангенс. В Delphi (и не только) для этих целей используется функция ArcTan2 из модуля math. Она корректно возвращает знак ± угла в зависимости от квадранта, а также предусмотрительно нечувствительна к возможным коллизиям, типа деления на 0.
Находим синус и косинус от требуемого угла β и подставляем в параметры функции ArcTan2, согласно последней формуле (4):
Эллипс и его свойства

Также эллипс можно определить как:
Содержание
Связанные определения
Соотношения между элементами фигуры

 |  |  |  |  |  | |
|---|---|---|---|---|---|---|
 — большая полуось — большая полуось |  |  |  |  |  |  |
 — малая полуось — малая полуось |  |  |  |  |  |  |
 — фокальное расстояние — фокальное расстояние |  |  |  |  |  |  |
 — фокальный параметр — фокальный параметр |  |  |  |  |  |  |
 — перифокусное расстояние — перифокусное расстояние |  |  |  |  |  |  |
 — апофокусное расстояние — апофокусное расстояние |  |  |  |  |  |  |
Координатное представление
Длина дуги эллипса
Длина дуги плоской линии определяется по формуле:
Воспользовавшись параметрическим представлением эллипса получаем следующее выражение:
После замены 

Приближённые формулы для периметра
Максимальная погрешность этой формулы
0,63 % при эксцентриситете эллипса
0,988 (соотношение осей
1/6,5). Погрешность всегда положительная.
Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула:

Максимальная погрешность этой формулы
0,36 % при эксцентриситете эллипса
0,980 (соотношение осей
1/5). Погрешность также всегда положительная.
Существенно лучшую точность при 
При эксцентриситете эллипса
0,980 (соотношение осей
1/5) погрешность составляет
0,02 %. Погрешность всегда отрицательная.
Еще точней оказалась вторая формула Рамануджана:
Точные формулы для периметра
Джеймс Айвори и Фридрих Бессель независимо друг от друга получили формулу для периметра эллипса:
где 



Площадь эллипса
Площадь эллипса вычисляется по формуле

Если эллипс задан уравнением