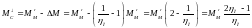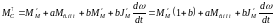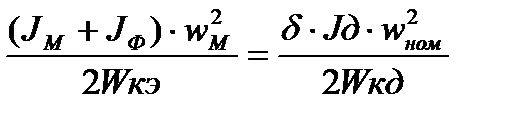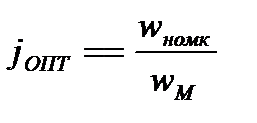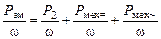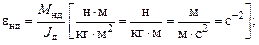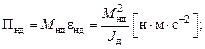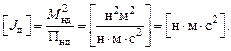учет потерь в механических передачах
13 Учет потерь в передаче.
Потери энергии (мощности) в передаче учитывают двумя способами:
1) приближенным, т.е. с помощью КПД и 2) уточненным, т.е. непосредственным вычислением составляющих потерь. Рассмотрим эти способы.
А. Учет потерь в передачах с помощью КПД.
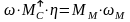
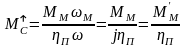
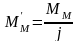
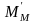
Для тормозного режима будем иметь такое равенство
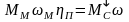
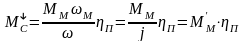
Но КПД 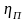
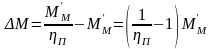
Примем допущение, что в тормозном режиме будет такая же потеря момента. Тогда статический момент в тормозном режиме можно записать в таком виде:
1) 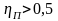
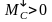
2) 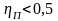
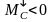
Потери момента в передаче приближенно выражаются через две составляющие, одна из которой для данной передачи является постоянной величиной, а вторая – пропорциональна передаваемому моменту:
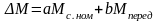
где 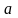
b – коэффициент переменных потерь;
Мс.ном – номинальный статический момент передачи;
Мперед – передаваемый момент, который равен моменту на выходном (по направлению передачи энергии) валу передачи.
Для установившегося двигательного режима 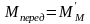
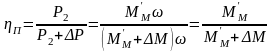
где 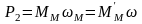
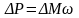
P2 – мощность на выходном валу ПМ в установившемся двигательном режиме;
P – потери мощности в передаче.
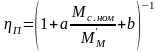
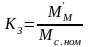
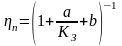
При номинальной нагрузке КЗ=1 и
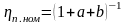
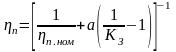
Таким образом, КПД передачи является функцией коэффициента загрузки и номинального КПД, так как коэффициент постоянных потерь зависит от номинального КПД и для ряда передач приводится в справочниках.
14. Уточненный метод учета потерь в передаче.
Рассмотрим сначала установившийся режим работы. Для двигательного установившегося режима имеем:
, 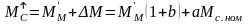
Для тормозного установившегося режима (см. Рис.1.17):
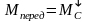
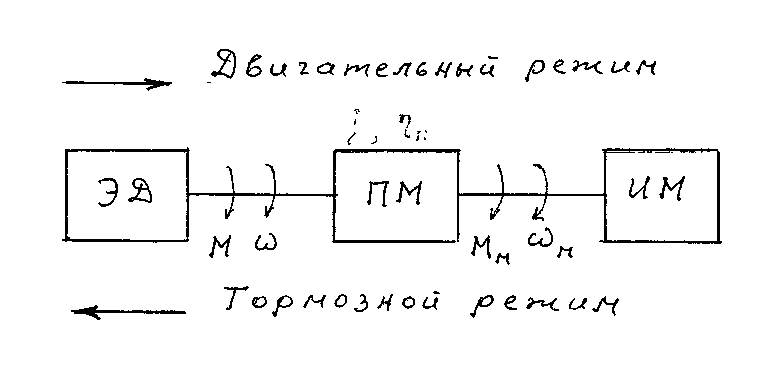
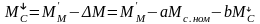
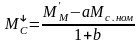
Теперь перейдем к переходным режимам. Для двигательного режима в переходном процессе (разгон)
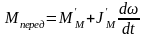
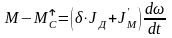
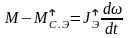
где 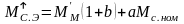
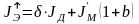
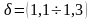
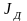
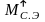
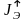
Для тормозного режима в переходном процессе
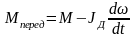
где М – момент электродвигателя в переходном процессе,
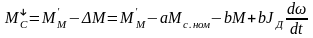
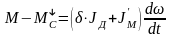
находим 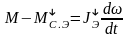
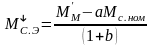
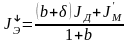
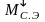
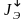
Заметим, что эквивалентные статические моменты при разгоне и торможении электропривода равны статическим моментам для установившихся двигательного и тормозного режимов. Самое важное состоит в том, что непосредственный учет потерь в передаче привел к тому, что эквивалентный момент инерции при разгоне электропривода стал больше, а при торможении меньше суммарного момента инерции электропривода. Получилось, что инерционность электропривода зависит, при прочих неизменных условиях, от режима работы.
Сложность непосредственного расчета потерь в передаче состоит в том, что необходимо иметь значения коэффициентов и b.
ОПТИМАЛЬНОЕ ПЕРЕДАТОЧНОЕ ЧИСЛОПО КРИТЕРИЮ минимум габарита ЭД
при отсуствии нагрузки на выходном валу
фиктивный момент инее
рции
тогда 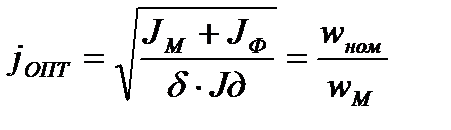
УЧЕТ ПОТЕРЬ В ПЕРЕДАЧЕ.
Потери энергии (мощности) в передаче учитывают двумя способами:
1) приближенным, т.е. с помощью КПД и 2) уточненным, т.е. непосредственным вычислением составляющих потерь. Рассмотрим эти способы.
А. Учет потерь в передачах с помощью КПД.




Для тормозного режима будем иметь такое равенство

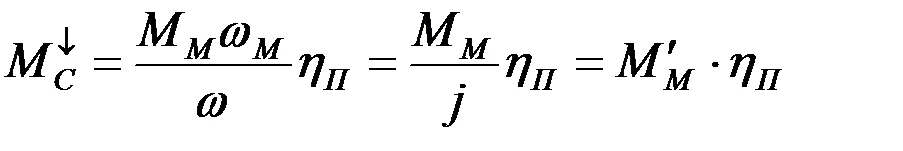
Но КПД 
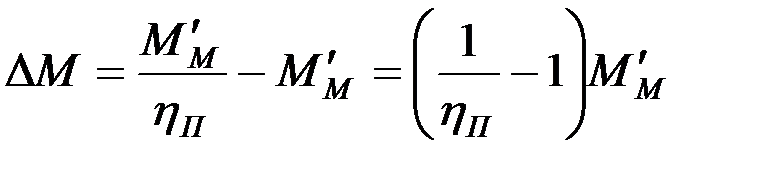
Примем допущение, что в тормозном режиме будет такая же потеря момента. Тогда статический момент в тормозном режиме можно записать в таком виде:
1) 

2) 

Потери момента в передаче приближенно выражаются через две составляющие, одна из которой для данной передачи является постоянной величиной, а вторая – пропорциональна передаваемому моменту:
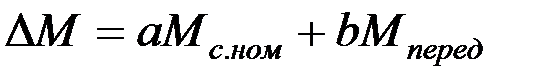
где 
b – коэффициент переменных потерь;
Мс.ном – номинальный статический момент передачи;
Мперед – передаваемый момент, который равен моменту на выходном (по направлению передачи энергии) валу передачи.
Для установившегося двигательного режима 

где 

P2 – мощность на выходном валу ПМ в установившемся двигательном режиме;
DP – потери мощности в передаче.



При номинальной нагрузке КЗ=1 и


Таким образом, КПД передачи является функцией коэффициента загрузки и номинального КПД, так как коэффициент постоянных потерь 
14. Уточненный метод учета потерь в передаче.
Рассмотрим сначала установившийся режим работы. Для двигательного установившегося режима имеем:


Для тормозного установившегося режима (см. Рис.1.17):

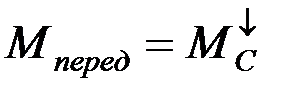

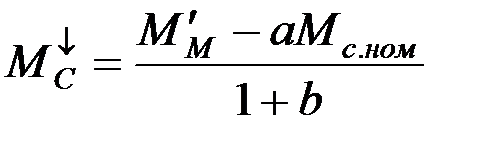
Теперь перейдем к переходным режимам. Для двигательного режима в переходном процессе (разгон)



где 


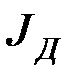


Для тормозного режима в переходном процессе
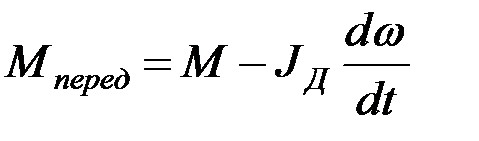
где М – момент электродвигателя в переходном процессе,


находим 

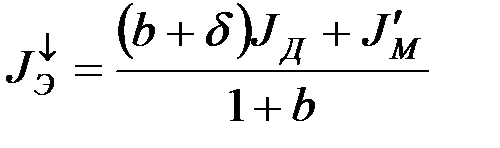


Заметим, что эквивалентные статические моменты при разгоне и торможении электропривода равны статическим моментам для установившихся двигательного и тормозного режимов. Самое важное состоит в том, что непосредственный учет потерь в передаче привел к тому, что эквивалентный момент инерции при разгоне электропривода стал больше, а при торможении меньше суммарного момента инерции электропривода. Получилось, что инерционность электропривода зависит, при прочих неизменных условиях, от режима работы.
Сложность непосредственного расчета потерь в передаче состоит в том, что необходимо иметь значения коэффициентов 
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Учет потерь в механической части ЭМС
Общие потери механической части ЭМС состоят из потерь в двигателе и потерь в редукторе. Как известно, в любом двигателе можно определить электромагнитную мощность, т.е. мощность, созданную в воздушном зазоре, если от Рпотр или Р1 вычесть потери SР, компенсируемые сетью
Электромагнитная мощность преобразуется в механическую, в том числе Рмех, т.е.
Потери в общем случае могут быть представлены:
постоянной и переменной частями. Ясно, что справедливо выражение
В ПУ также потери разделяют на постоянные, не зависящие от полезной нагрузки, и переменные, зависящие от передаваемой нагрузки. В справочниках приведены зависимости КПД одноступенчатых зубчатых передач. Тогда приведенный статический момент определяют
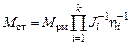
Энергодинамические характеристики
Силовой части приводов постоянного тока
Определяющими энергетическими и динамическими характеристиками являются:
Мн – основная силовая характеристика (номинальный момент на выходном валу);
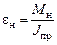
Пн = Мнeн (номинальная приемистость) – обобщенная энергодинамическая характеристика.
Анализ потоков энергии в ЭМС типа импульсный преобразователь-двигатель-редуктор, в основу которого положены удельные показатели: относительная масса, относительное ускорение (добротность), приемистость:
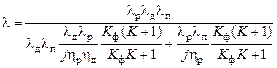
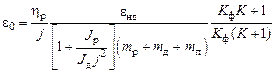
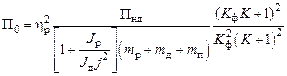
где 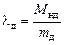
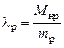
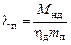
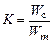
На технические характеристики существенное влияние оказывают параметры, характеризующие уровень согласования элементов ЭМС
(j, K, Kф). Определение их рациональных значений представляет собой многокритериальную задачу, которая обычно решается способом последовательного достижения частных целей (т.е. выделяются отдельные звенья, например, Пр-ДПТ, ДПТ-редуктор и т.д.).
О выборе типа ЭМС
От свойств и характеристик ЭМС зависит производительность и качество выпускаемой продукции. Выбор типа ЭМС согласуется с требованиями, предъявляемыми к рабочим механизмам и агрегатам. Сложность современных производственных машин и агрегатов не позволяет составить уравнения, определяющие их поведение, исходя из физических принципов функционирования и конструктивных данных.
Приходится выявлять необходимые характеристики и параметры, исследуя поведение рабочей машины при выполнении технологического процесса. Для более глубокого знакомства с условиями работы производственного механизма разрабатывается техническое задание, в котором учитываются все особенности технологического процесса и условия работы исполнительного механизма. В техническом задании должны найти отражение вопросы, касающиеся характера статического момента, необходимых пределов регулирования скорости, плавности регулирования, стабильности скорости, допустимого её отклонения от среднего значения, требуемого набора механических характеристик, условий пуска и торможения, характера переходных процессов и др.
Для нерегулируемой ЭМС выбор типа двигателя и системы управления решается достаточно просто. Для установок малых и средних мощностей используются асинхронные двигатели с короткозамкнутым ротором, а для механизмов, требующих больших мощностей – синхронные двигатели. Двигатели переменного тока по конструкции проще, стоимость их ниже, они надежнее и обслуживание их требует меньших затрат. Синхронные двигатели используются и в области ма-лых мощностей для специальных установок и в устройствах автоматики. Свойство синхронного двигателя поддерживать неизменным средний уровень скорости является определяющим при использовании их в лентопротяжных механизмах, устройствах отработки времени, модуляторах светового потока и др.
Значительно сложнее решать вопрос о выборе типа двигателя для регулируемой ЭМС. Здесь необходимо указывать допустимые погрешности при набросе нагрузки и предельные коэффициенты неравномерности частоты вращения на различных уровнях, необходимые полосы пропускания частот для контура скорости и контура положения, разрешенные неравномерности скорости и др.
При глубоком регулировании частоты вращения и необходимости иметь хорошую управляемость возможно использование только ЭМС с индивидуальными преобразователями. В настоящее время широко используются ЭМС с частотным и частотно-токовым управлением. Основными препятствиями к быстрому и широкому внедрению частотно-регулируемых ЭМС являются сложность систем управления и отсутствие специальных двигателей, предназначенных для работы в условиях переменой частоты.
Необходимо отметить, что в связи с быстрым развитием полупроводниковой техники, электромашиностроения и появлением новых аппаратных средств регулируемые ЭМС непрерывно совершенствуются и следует ожидать появления новых с улучшенными техническими показателями.
Список литературы
1. Анализ и синтез ЭМС / А.И. Ильин, Б.Р. Липай, С.И. Маслов, П.А. Тыричев. – М.: Изд-во МЭИ, 1999. – 76 с.
2. Афонин С.М. Расчет элементов и устройств ЭМС. – М.: МЭИ, 2000. –
75 с.
3. Егоров Н.В. ЭМС. Общие принципы анализа и расчета ЭМС: Уч. пособие / Н.В. Егоров, Д.А. Овсянников; СПб. гос. ун-т. – СПб.: СПбГУ, 2002. –
117 с.
4. Ковчин С.А., Сабинин Ю.А. Теория электропривода.– СПб.: Энергоатомиздат, 1994. – 496 с.
5. Ленк А. Электромеханические системы. – М.: Мир, 1978. – 283 с.
6. Липай Б.Р. Компьютерные модели ЭМС. – М.: МЭИ, 2003. – 102 с.
7. Львович А.Ю. Электромеханические системы. – Л.: Изд-во ЛГУ, 1986. – 296 с.
8. Маслов С.И., Тыричев П.А. Электромеханические системы. – М.: Изд-во МЭИ, 1999. –100 с.
9. Маслов С.И., Тыричев П.А. Силовые элементы ЭМС. – М.: Изд-во МЭИ, 1999. – 128 с.
10. Сабинин Ю.А. Позиционные и следящие ЭМС: Уч. пособие для вузов. – СПб: Энергоатомиздат, 2001. – 207 с.
11. Чабан В.И. Методы анализа электромеханических систем. – Вища шк., 1985. – 192 с.