Как сделать выпуклый многоугольник

Выпуклый многоугольник

Что такое выпуклый многоугольник? В чём отличие выпуклого многоугольника от многоугольника, который не является выпуклым?

Выпуклый многоугольник — это многоугольник, лежащий в одной полуплоскости от каждой прямой, содержащей его сторону.

То есть ни одна из прямых, проходящих через две соседние вершины выпуклого многоугольника, не разрезает этот многоугольник на две части.

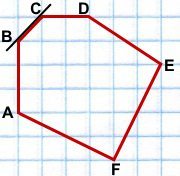
1) ABCDEF — выпуклый шестиугольник, так как он лежит в одной полуплоскости относительно каждой из прямых AB, BC, CD, DE и EF.

2) MNKFEL — не выпуклый шестиугольник,

Он не лежит в одной полуплоскости относительно прямых KF и FE.

Не выпуклый многоугольник можно разбить на конечное число выпуклых многоугольников. Поэтому в курсе геометрии средней школы изучают только выпуклые многоугольники.

Важнейшие виды выпуклых многоугольников

Источник

Построение минимальных выпуклых оболочек

Проведя небольшое научное исследование (проще говоря, выполнив поиск на сайте), обнаружил, что на хабре имеется всего две статьи с тегом вычислительная геометрия, причем одна из них оказалась моей. Т.к. в последнее время я несколько заинтересовался этой тематикой, то решил продолжить тему алгоритмической геометрии рассмотрением задачи построения так называемых минимальных выпуклых оболочек. Хотя рисунок справа и дает проницательному хаброчитателю исчерпывающее объяснение того, что это такое, тем не менее под катом будут даны чуть более формальные определения и описаны два классических алгоритма построения минимальных выпуклых оболочек.

Понятие минимальной выпуклой оболочки

Пусть на плоскости задано конечное множество точек A. Оболочкой этого множества называется любая замкнутая линия H без самопересечений такая, что все точки из A лежат внутри этой кривой. Если кривая H является выпуклой (например, любая касательная к этой кривой не пересекает ее больше ни в одной точке), то соответствующая оболочка также называется выпуклой. Наконец, минимальной выпуклой оболочкой (далее кратко МВО) называется выпуклая оболочка минимальной длины (минимального периметра). Я не проверял (похоже, это можно доказать от противного), но кажется очевидным, что минимальная оболочка просто обязана быть выпуклой. Все введенные понятия иллюстрируются следующим рисунком.

Главной особенностью МВО множества точек A является то, что эта оболочка представляет собой выпуклый многоугольник, вершинами которого являются некоторые точки из A. Поэтому задача поиска МВО в конечном итоге сводится к отбору и упорядочиванию нужных точек из A. Упорядочивание является необходимым по той причине, что выходом алгоритма должен быть многоугольник, т.е. последовательность вершин. Наложим дополнительно условие на порядок расположения вершин — направление обхода многоугольника должно быть положительным (напомню, что положительным называется обход фигуры против часовой стрелки).

Задача построения МВО считается одной из самых простых задач вычислительной геометрии, для нее существует много различных алгоритмов. Ниже мы рассмотрим два таких алгоритма — Грэхема (Graham scan) и Джарвиса (Jarvis march). Их описание иллюстрируется кодом на Питоне. Обоим алгоритмам потребуется функция rotate, побробно описанная в предыдущем моем посте. Напомню, что эта функция определяет, с какой стороны от вектора AB находится точка C (положительное возвращаемое значение соответствует левой стороне, отрицательное — правой).

Алгоритм Грэхема (Graham scan)

Этот алгоритм является трехшаговым. На первом шаге ищется любая точка в A, гарантированно входящая в МВО. Нетрудно сообразить, что такой точкой будет, например, точка с наименьшей x-координатой (самая левая точка в A). Эту точку (будем называть ее стартовой) перемещаем в начало списка, вся дальнейшая работа будет производиться с оставшимися точками. По некоторым соображениям, исходный массив точек A нами меняться не будет, для всех манипуляций с точками будем использовать косвенную адресацию: заведем список P, в котором будут хранится номера точек (их позиции в массиве A). Итак, первый шаг алгоритма заключается в том, чтобы первой точкой в P оказалась точка с наименьшей x-координатой. Код:

Второй шаг в алгоритме Грэхема — сортировка всех точек (кроме P[0]-ой), по степени их левизны относительно стартовой точки R=A_P[0]. Будем говорить, что B * рук), я буду использовать сортировку вставками.
*_{я буду очень признателен тем, кто сможет мне объяснить, как применить в данном случае встроенную питоновскую сортировку.}
Итак, сортировка вставками (не забываем про косвенную адресацию и про то, что нулевая точка не сортируется):

Результат сортировки можно проиллюстрировать следующим рисунком.

Если мы теперь соединим точки в полученном порядке, то получим многоугольник, который, однако, не является выпуклым.

Переходим к третьему действию. Все, что нам осталось сделать, так это срезать углы. Для этого нужно пройтись по всем вершинам и удалить те из них, в которых выполняется правый поворот (угол в такой вершине оказывается больше развернутого). Заводим стек S (реально список) и помещаем в него первые две вершины (они, опять же, гарантированно входят в МВО).

Затем просматриваем все остальные вершины, и отслеживаем направление поворота в них с точки зрения последних двух вершин в стеке S: если это направление отрицательно, то можно срезать угол удалением из стека последней вершины. Как только поворот оказывается положительным, срезание углов завершается, текущая вершина заносится в стек.

В итоге в стеке S (который теперь можно рассматривать, как список) оказывается искомая последовательность вершин, причем в нужной нам ориентации, определяющая МВО заданного множества точек A.

Сложность первого и последнего шагов алгоритма является линейной по n (хотя в последнем случае имеется вложенный цикл, однако, каждая вершина внутри этого цикла ровно один раз заносится в стек, и не более одного раза оттуда удаляется), следовательно, сложность всего алгоритма определяется вторым шагом — сортировкой, именно поэтому сортировка вставкой оказывается не лучшим вариантом при больших n. Если ее заменить на быструю сортировку, то получим суммарную сложность алгоритма O(nlogn). Можно ли улучшить это время? Если алгоритм основан на попарном сравнении точек (как у нас), то доказано, что данная оценка в общем случае не улучшаема. С этой точки зрения алгоритм Грэхема оптимален. Тем не менее у него имеется не очень хорошая особенность — он не является адаптивным в том смысле, что не важно, сколько вершин в итоге войдет в МВО (три, пять, десять или n), все равно время будет линейно-логарифмическим. Такой адаптивностью обладает алгоритм Джарвиса, к рассмотрению которого мы плавно и переходим.

Алгоритма Джарвиса

Алгоритм Джарвиса (другое название — алгоритм заворачивания подарков) концептуально устроен проще алгоритма Грэхема. Он является двухшаговым и не требует сортировки. Первый шаг точно такой же — нам нужна стартовая точка, которая гарантированно входит в МВО, берем самую левую точку из A.

На втором шаге алгоритма строится МВО. Идея: делаем стартовую вершину текущей, ищем самую правую точку в A относительно текущей вершины, делаем ее текущей и т.д. Процесс завершается, когда текущей вновь окажется стартовая вершина. Как только точка попала в МВО, больше ее можно не учитывать. Поэтому заведем еще один список H, в котором в правильном порядке будут храниться вершины МВО. В этот список сразу же заносим стартовую вершину, а в списке P эту вершину переносим в конец (где мы ее в конце концов найдем и завершим алгоритм).

Теперь организуем бесконечный цикл, на каждой итерации которого ищем самую левую точку из P относительно последней вершины в H. Если эта вершина стартовая, то прерываем цикл, если нет — то переносим найденную вершину из P в H. После завершения цикла в H находится искомая оболочка, которую мы и возвращаем в качестве результата.

Хм, мне удалось рассказать об алгоритме Джарвиса, не используя картинок. Следующий рисунок иллюстрирует все!

Оценим сложность алгоритма Джарвиса. Первый шаг линеен по n. Со вторым все интереснее. У нас имеется вложенный цикл, число внешних итераций равно числу вершин h в МВО, число внутренних итераций не превышает n. Следовательно, сложность всего алгоритма равна O(hn). Необычным в этой формуле является то, что сложность определяется не только длиной входных данных, но и длиной выхода (output-sensitive algorithm). А дальше как карты точки лягут. В худшем случае все точки из A входят в МВО (т.е. A уже само по себе выпуклый многоугольник), тогда h=n и сложность подскакивает до квадратичной. В лучшем случае (при условии, что точки из A не лежат на одной прямой) h=3 и сложность становится линейной. Осталось заранее понять, какой у нас случай, что сделать не так просто (если у вас нет машины времени ** ), можно только исходить из характера задачи — если точек много и они равномерно заполняют некоторую область, то (возможно) Джарвис будет быстрее, если же данные собраны на границе области, то быстрее будет Грэхем, как-то так…
**_{Машина времени вообще полезная штука с точки зрения алгоритмов, любая задача, требующая триллиона лет вычислений, с ее помощью может быть решена практически мгновенно — запускаем программу, садимся в машину времени, «летим» в будущее, считываем результат, возвращаемся назад. Осталось придумать, как обеспечить бесперебойную работу компьютера на пару триллионов лет.}

Вместо заключения

На мой взгляд, задача построения минимальных выпуклых оболочек — хороший способ войти в тему вычислительной геометрии, достаточно легко придумать свой собственный алгоритм (однако, наверняка это будет вариация алгоритма Джарвиса). Утверждается, что приложений у этой задачи много, большая их часть связана с распознаванием образов, кластеризацией и т.п. Кроме того, задача построения МВО используется в качестве вспомогательного средства при решении более сложных задач вычислительной геометрии. Да, стоит отметить, что у этой задачи имеется весьма интересное трехмерное обобщение.

Источник

Многоугольники (ЕГЭ 2022)

Никогда не было интересно, почему в треугольнике 180 градусов?

А в других фигурах сколько? Да постой, положи транспортир!

Сейчас ты узнаешь много нового о такой, казалось бы, простой теме, как многоугольники.

Многоугольники — коротко о главном

Многоугольник – это замкнутая линия, которая образовывается, если взять \( \displaystyle n\) каких-либо точек \( \displaystyle <_<1>>,\text< ><_<2>>,\text< >…,

Многоугольник с \( \displaystyle n\) сторонами называют \( \displaystyle n\)-угольником.

Например: многоугольник c \( \displaystyle 4\) сторонами называют четырехугольником, многоугольник с \( \displaystyle 6\) сторонами — шестиугольником и так далее по аналогии.

Выпуклый многоугольник – многоугольник лежащий по одну сторону от любой прямой, соединяющей его соседние вершины.

Сумма внутренних углов выпуклого n-угольника равна \( \displaystyle 180<>^\circ \cdot (n-2)\) или \( \displaystyle <<\alpha >_<1>>+<<\alpha >_<2>>+\text< >…

Правильный выпуклый многоугольник – многоугольник все стороны и внутренние углы которого равны.

Внутренний угол правильного \( \displaystyle n\)-угольника равен \( \displaystyle \alpha =\frac\cdot 180<>^\circ \).

Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.

Центры вписанной в правильный многоугольник окружности и окружности, описанной около него, совпадают.

Если многоугольник такой, что в него можно вписать окружность, то его площадь выражается формулой: \( \displaystyle S=pr\), где \( \displaystyle p=\frac<<_<1>><_<2>>+<_<2>><_<3>>+…+<_><_<1>>><2>\).

Многоугольник — подробнее

Многоугольник – это замкнутая линия, которая образовывается, если взять \( \displaystyle n\) каких-либо точек \( \displaystyle <_<1>>,\text< ><_<2>>,\text< >…,

При этом смежные стороны (имеющие общую вершину) не должны лежать на одной прямой, а несмежные стороны не должны иметь общих точек (то есть не должны пересекаться).

Многоугольник с \( \displaystyle n\) сторонами называют \( \displaystyle n\)-угольником.

Произвольные многоугольники

Давай-ка нарисуем, какие бывают многоугольники.

А теперь вопрос: какой из этих многоугольников выпадает из ряда?

Посмотри внимательно на второй многоугольник — он отличается от всех остальных. Чем же?

Это не выпуклый многоугольник. Это, конечно, математическое название, но с человеческой интуицией не расходится.

Ну вот, а мы будем рассматривать только выпуклые многоугольники, то есть такие, как 1),3),4) и т.п.

Итак, основной факт:

В любом многоугольнике сумма внутренних углов равна \( \displaystyle 180^o(n-2)\), где буква «\( \displaystyle n\)» означает число углов многоугольника.

Давай сразу к примерам:

Четырехугольник

Пятиугольник

Шестиугольник

Ах да, про треугольник забыли.

Треугольник

Сумма углов многоугольника. Доказательство.

А теперь давай все-таки разберемся, откуда же взялась формула суммы углом многоугольника \( \displaystyle 180^\circ(n-2)\).

Понимаешь, приемчик, который мы сейчас применим, часто оказывается полезным при решении разных задач.

Несмотря на то, что теорема о сумме углов многоугольника верна для всякого многоугольника, доказательство красивое и простое только для выпуклых многоугольников.

Итак, давай разделим многоугольник на треугольники.

Вот так: из одной точки проведем все диагонали, что можно. Сколько их будет? Считаем:

Всего вершин: \( \displaystyle n\)

Из вершины \( \displaystyle B\) можем провести диагонали во все вершины, кроме:

Значит всего диагоналей \( \displaystyle (n-3)\). А на сколько треугольников распался наш многоугольник?

Представь себе: на \( \displaystyle n-2\). Порисуй, посчитай – удостоверься, что треугольников оказывается ровно на один больше.

Итак, у нас ровно \( \displaystyle n-2\) треугольника. И сумма углов многоугольника просто равна сумме углов треугольников, на которые мы разбили многоугольник.

Чему равна сумма углов треугольника? Помнишь? Конечно \( \displaystyle 180<>^\circ \).

Ну вот, \( \displaystyle n-2\) треугольника, в каждом по \( \displaystyle 180<>^\circ \), значит:

Сумма углов многоугольника равна \( \displaystyle 180<>^\circ \)\( \displaystyle (n-2)\)

Что же из этого может оказаться полезным? Два момента:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Правильные многоугольники

Многоугольник называется правильным, если все его углы и все его стороны равны.

Так, например: квадрат – правильный четырехугольник, а вот прямоугольник – нет, хоть и все углы у него равные, и ромб – нет, хоть и все стороны равны. Нужно непременно, чтобы все углы и все стороны были равны.

Первый вопрос:

А можно ли найти величину одного (а значит и всех) угла правильного многоугольника?

Давай посмотрим на примере.

Пусть есть, скажем, правильный восьмиугольник:

Сумма всех его углов равна \( \displaystyle 180<>^\circ \left( 8-2 \right)=1080<>^\circ \).

А сколько всего углов? Восемь конечно, и они все одинаковые.

Значит любой угол, скажем \( \displaystyle \angle A\) можно найти:

\( \displaystyle \angle A=\frac<1080<>^\circ ><8>=135<>^\circ \).

Что мы еще должны знать?

Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.

При этом центры этих окружностей совпадают.

Смотри, как это выглядит!

И более того, всегда можно посчитать соотношение между радиусом вписанной и описанной окружностей.

Давай опять на примере восьмиугольника.

Посмотри на \( \displaystyle \Delta OKG\). В нем \( \displaystyle OK=r,OG=R.\)

Значит, \( \displaystyle \frac=\sin \angle x\) – и это не только в восьмиугольнике!

Чему же равен в нашем случае \( \displaystyle \angle x\)?

Ровно половине \( \displaystyle \angle G\), представь себе!

Значит \( \displaystyle \angle x=\frac<135<>^\circ ><2>=67,5<>^\circ \).

Смешно? Но так и есть! Поэтому для восьмиугольника \( \displaystyle \frac=\sin 67,5<>^\circ \).

Может возникнуть еще один вопрос: а можно ли посчитать углы «около» точки \( \displaystyle O\)?

И тот же ответ: конечно можно!

Опять рассмотрим наш восьмиугольник. Вот мы хотим найти \( \displaystyle \angle \alpha\) (то есть \( \displaystyle \angle HOG\)).

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

И так можно все находить не только для восьмиугольника, но и для любого правильного многоугольника.

Бонус. Вебинар из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 6. Описанная окружность. Многоугольники

Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства.

Около каких фигур можно, а вокруг каких нельзя описать окружность.

Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.

Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.

А теперь твоя очередь!

Теперь ты знаешь все о многоугольниках!

Особенно эти знания пригодятся тебе, когда будешь решать задачи про окружности. Задачи олимпиадного уровня. Да и просто так знать полезно 🙂

А сейчас мы хотим услышать тебя. Понравилась ли тебе статья? Ты во всем разобрался?

Кстати, пытался строить многоугольники циркулем?

Напиши в комментариях ниже!

И задай любые вопросы, если они возникли! Мы непременно ответим!

Добавить комментарий Отменить ответ

3 комментария

Як разбить чатырох угольник так, чтоб палучился трохвугольник и чатырохвугольник

Даша, например, можно провести отрезок из вершины в середину противоположной стороны.

Некоторые комментарии прошлых лет к этой статье:

Сергей
19 февраля 2018
Просто огромное спасибо. Хоть что-то начал понимать.

Александр (админ)
19 февраля 2018
Просто огромное пожалуйста. 🙂 Очень приятно слышать от вас такие слова.

Вероника
18 марта 2020
Спасибо большое, а то на карантине приходится самим разбирать темы!

Александр (админ)
18 марта 2020
Отлично, Вероника! Круто, что ты сама пытаешься разобраться с математикой! Этот навык ой как пригодится в будущем. Я всегда говорю: «В жизни репетитора и учителя рядом не будет». И я рад, что наш скромный сайт в этом помогает. Удачи на экзаменах! Все будет хорошо!

Сима
01 июля 2020
Блин, действительно очень круто изложили. А главное- понятно и просто. Начала подготовку к егэ, в следующем году сдавать. Очень помогли разобраться с этой темой! Спасибо)

Александр (админ)
01 июля 2020
Блин, Сима, до чертиков приятно слышать такие слова! 🙂 Если начала подготовку к ЕГЭ, то будь на связи, мы сейчас делаем крутейший курс подготовки к ЕГЭ, где вот так вот просто все будет объяснять Алексей Шевчук.

Источник

Многоугольник

Определение 1. Многоугольник − замкнутая ломаная линия.

Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:

Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.

Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.

Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.

Виды многоугольников

Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.

На рисунке 1 представлены различные виды многоугольников.

Обозначение многоугольника

Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).

Соседние вершины многоугольника

Вершины многоугольника называются соседними, если они являются концами одной из его сторон.

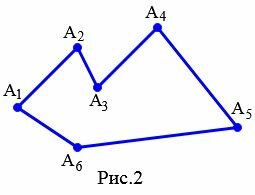На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)

Смежные стороны многоугольника

Стороны многоугольника называются смежными, если они имеют общую вершину.

На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)

Простой многоугольник. Самопересекающийся многоугольник

Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

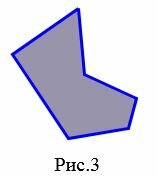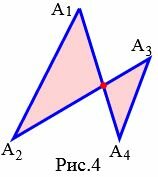На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.

Выпуклый многоугольник

Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

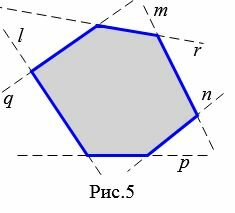На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.

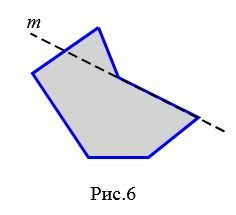На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.

Правильный многоугольник

Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.

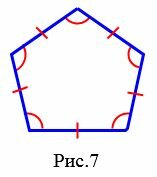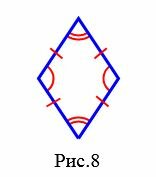На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Звездчатый многоугольник

Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.

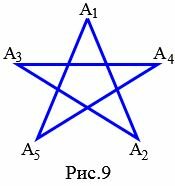На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)

Периметр многоугольника

Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_A_n \) периметр вычисляется из формулы:

Угол многоугольника

Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).

Внешний угол многоугольника

Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.

На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)

Диагональ многоугольника. Количество диагоналей

Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.

Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:

Сумма углов выпуклого многоугольника

Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_A_n \) (Рис.11):

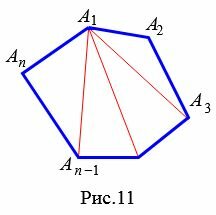Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)

где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.

Угол правильного многоугольника

Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:

где \( \small n \) −количество сторон (вершин) правильного многоугольника.

Источник