Как рисуется равнобедренный треугольник
Узнать ещё
Знание — сила. Познавательная информация
Как нарисовать равносторонний треугольник
Как нарисовать равносторонний треугольник, используя только линейку и карандаш? Этот способ позволяет быстро сделать рисунок правильного или равнобедренного треугольника.
Как нарисовать равнобедренный треугольник
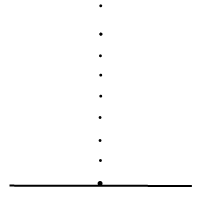
Рисунок начинаем с основания. Длину основания подбираем такой, чтобы ее удобно было делить пополам (берем четное количество клеточек). Вершину треугольника отмечаем ровно над серединой основания:
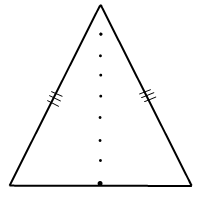
Если нужен равнобедренный треугольник, у которого боковая сторона больше основания, вершину ставим повыше:
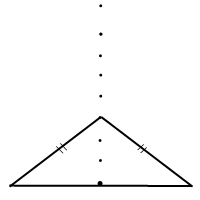
Если требуется треугольник, основание которого больше боковой стороны, то вершину отмечаем ниже:
Как нарисовать равносторонний треугольник
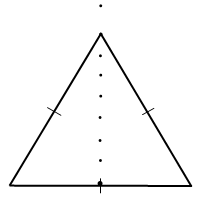
От конца основания откладываем отрезок равной ему длины так, чтобы второй конец этого отрезка расположился ровно над серединой основания. Соединяем вершину треугольника с другим концом основания:
Если в задаче о равнобедренном треугольнике речь идет о высоте, биссектрисе и медиане, проведенным к основанию, достаточно соединить вершину треугольника с отмеченной серединой основания:
Как построить равнобедренный треугольник
Как построить равнобедренный треугольник? Это легко сделать с помощью линейки, карандаша и клеточек тетради.
Построение равнобедренного треугольника начинаем с основания. Чтобы рисунок получился ровным, количество клеточек в основании должно быть четным числом.
Делим отрезок — основание треугольника — пополам.
Вершину треугольника можно выбрать на любой высоте от основания, но обязательно ровно над срединой.
Как построить остроугольный равнобедренный треугольник?
Углы при основании равнобедренного треугольника могут быть только острыми. Чтобы равнобедренный треугольник получился остроугольным, угол при вершине тоже должен быть острым.
Для этого вершину треугольника выбираем повыше, подальше от основания.
Чем выше вершина, тем меньше угол при вершине. Углы при основании при этом, соответственно, увеличиваются.
Как построить тупоугольный равнобедренный треугольник?
С приближением вершины равнобедренного треугольника к основанию градусная мера угла при вершине увеличивается.
Значит, чтобы построить равнобедренный тупоугольный треугольник, вершину выбираем пониже.
Как построить равнобедренный прямоугольный треугольник?
Чтобы построить равнобедренный прямоугольный треугольник, надо вершину выбрать на расстоянии, равном половине основания (это обусловлено свойствами равнобедренного прямоугольного треугольника).
Например, если длина основания — 6 клеточек, то вершину треугольника располагаем на высоте 3 клеточек над серединой основания. Обратите внимание: при этом каждая клеточка у углов при основании делится по диагонали.
Построение равнобедренного прямоугольного треугольника можно начать с вершины.
Выбираем вершину, от нее под прямым углом откладываем равные отрезки вверх и вправо. Это — боковые стороны треугольника.
Соединим их и получим равнобедренный прямоугольный треугольник.
Построение равнобедренного треугольника с помощью циркуля и линейки без делений рассмотрим в другой теме.
Равнобедренный треугольник: свойства, признаки и формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!
Для доказательства следующих теорем нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
В каждом из доказательств мы пользуемся признаком равенства треугольников, вот и повод их повторить.
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, AH = HC и BH — медиана.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, AH = HC и BH — медиана.
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.
Не должно вас удивить и то, что сумма углов треугольника равна 180°.
∠B = 180° − 80° − 80° = 20°.
Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.
Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.
А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.
Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.
Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.
Как правильно рисовать треугольник
Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Как рисовать треугольник с равными сторонами?
Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.
Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Варианты создания фигуры
Обязательно используйте линейку и один из представленных ниже способов:
Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.
Рекомендации по построению равнобедренного треугольника
Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).
Как нарисовать равнобедренный треугольник:
Вписанный треугольник
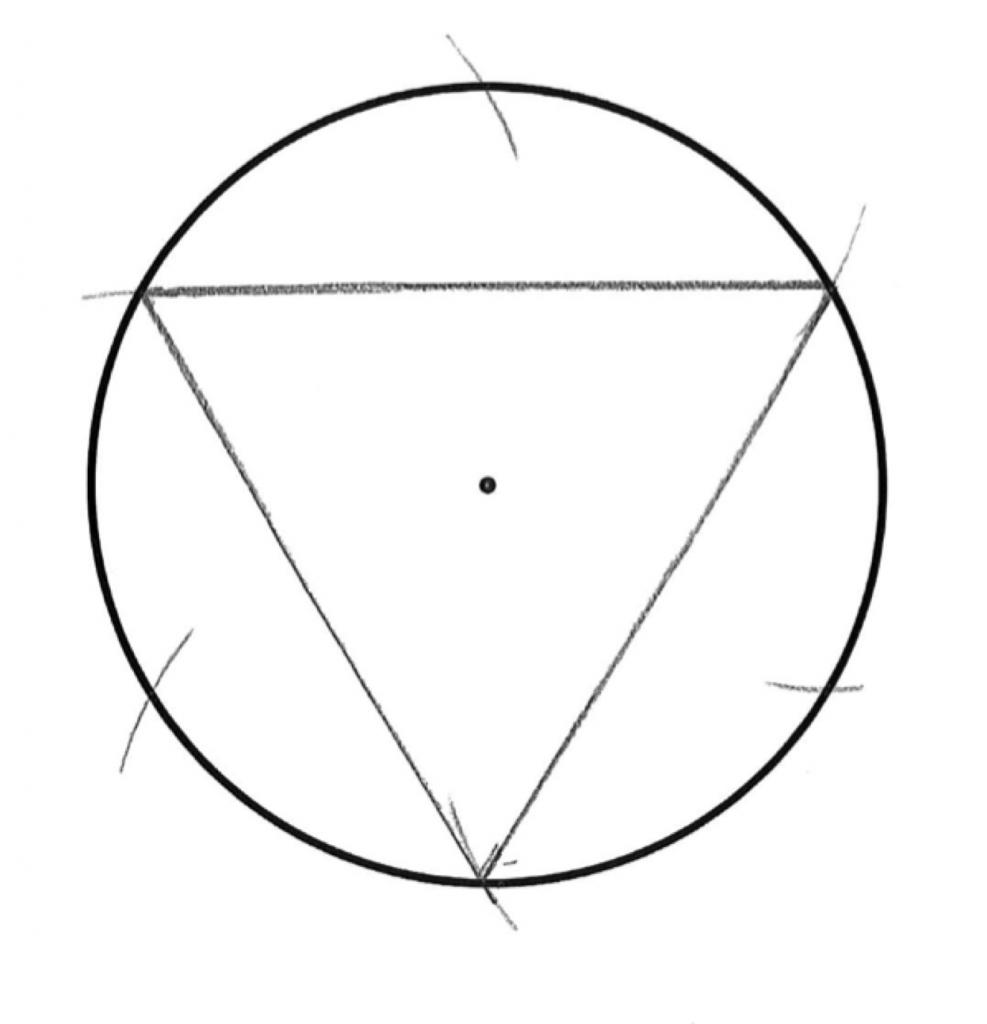
Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта – расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.
С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект – должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу – это четверть пути по окружности.
Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.
Подведем итоги
В статье были предоставлены рекомендации, как нарисовать треугольник равносторонний, равнобедренный и вписанный в окружность.
Знание — сила. Познавательная информация
Как нарисовать равносторонний треугольник
Как нарисовать равносторонний треугольник, используя только линейку и карандаш? Этот способ позволяет быстро сделать рисунок правильного или равнобедренного треугольника.
Как нарисовать равнобедренный треугольник
Рисунок начинаем с основания. Длину основания подбираем такой, чтобы ее удобно было делить пополам (берем четное количество клеточек). Вершину треугольника отмечаем ровно над серединой основания:
Если нужен равнобедренный треугольник, у которого боковая сторона больше основания, вершину ставим повыше:
Если требуется треугольник, основание которого больше боковой стороны, то вершину отмечаем ниже:
Как нарисовать равносторонний треугольник
От конца основания откладываем отрезок равной ему длины так, чтобы второй конец этого отрезка расположился ровно над серединой основания. Соединяем вершину треугольника с другим концом основания:
Если в задаче о равнобедренном треугольнике речь идет о высоте, биссектрисе и медиане, проведенным к основанию, достаточно соединить вершину треугольника с отмеченной серединой основания:
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Количество источников, использованных в этой статье: 6. Вы найдете их список внизу страницы.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
В равностороннем треугольнике все стороны и углы равны. Вручную нарисовать идеальный равносторонний треугольник довольно сложно. Но вы можете воспользоваться транспортиром, чтобы точно отложить углы. Также используйте линейку, чтобы проводить абсолютно прямые линии. Эта статья расскажет вам, как нарисовать равносторонний треугольник.
В каком порядке репетитор по математике рисует равнобедренный треугольник
Поговорим, казалось бы, о такой мелочи в системе преподавания геометрии 7 класса, как рисунок равнобедренного треугольника. Если Вы репетитор по математике – попросите Вашего ученика нарисовать такой треугольник. Как он это сделает? С вероятностью, равной 0,9 порядок проведения линий (сторон) на бумаге будет соответствовать последовательности расположения вершин треугольника в записи 
, то есть направлению стрелки, показанной на рисунке: 
Именно так (то есть по кругу) сам репетитор по математике обозначает вершины и именно этот порядок запоминается. Понаблюдаем за учеником. Сначала, скорее всего, он нарисует репетитору математики левую боковую сторону, затем правую, а уже после этого соединит их нижние точки и нарисует основание. Все бы ничего, да вот проблема: трудно изображать боковые стороны равными (особенно если использовать непрозрачную линейку) и поэтому рисунок часто получается несимметричным. И вот ученик уже работает ластиком (в лучшем случае) и, как следствие, тратит на чертеж драгоценное время (пусть незначительное, но все-таки). Хороший репетитор по математике стремится использовать каждую свободную минуту своего занятия и поэтому всегда уделяет внимание оптимизации самостоятельной работы учащегося. Использование методики готовых чертежей не является панацеей, тем более в период, когда ребенок учится в 7 классе. В этом возрасте он приобретает чертежные навыки, и если репетитор по математике будет баловать его готовыми чертежами, то при классических формах подачи заданий, составляющих большую часть контрольных работ, ученик может растеряться.
Поэтому важно научить быстро и точно выполнять стандартные рисунки. Но как?
Есть одно простое правило. Оно не только ускорит построение равнобедренного треугольника, но и будет способствовать запоминанию его главных характеристик и свойств. Я предполагаю, что для этого имеется бумага в клеточку, линейка и карандаш.
Как репетитор по математике рисует равнобедренный треугольник?
Необходимо начать с основания медианы, биссектрисы и высоты. То есть отмечается узел любой клетки (основание медианы), от которого влево и вправо репетитор по математике откладывает равные отрезки – половинки будущего основания. Их концы соединяются. Далее от центрального узла карандаш преподавателя «поднимается» вверх на некоторое количество клеток (большее длины основания). В узле последней клетки ставится точка – вершина равнобедренного треугольника. 
Вершина треугольника готова. Таким образом, будет построен «каркас» фигуры, вершины которой можно даже в некоторых ситуациях (при рисунке-наброске) соединить и от руки.
Какие девиденты приносит это построение репетитору по математике?
Каждый раз, когда ученик отмечает вершины по данному плану, репетитор по математике напоминает ему о том, что вертикальный отрезок есть ни что иное, как медиана, биссектриса и высота треугольника. Многократные построения и напоминания репетитора пойдут только на пользу ученику, ибо заставят вспомнить важнейшее свойство равнобедренного треугольника. Ученик поймет и запомнит форму изучаемой фигуры, особенности и взаимосвязи ее элементов. Сильный семиклассник задумается (или догадается спросить у репетитора) о том, почему построенный таким образом треугольник обязательно окажется равнобедренным.
Часто в задачах по геометрии в 7 классе фигурирует произвольный треугольник. Я всегда советую своим ученикам строить его так, чтобы они значительно отличался по виду от равнобедренного. Почему? Если от центральной точки (от основания высоты), отложить влево и вправо разные отрезки даже с разницей в клетку, то, несмотря на несовпадение медианы с высотой, образованные ими треугольники окажутся чрезвычайно узкими и поэтому неудобными для любых демонстраций. Репетитор по математике просто не сможет в них ничего показать. Посмотрите, насколько близко оказываются друг от друга отрезки BH, BN и BM на рисунке, изображенном слева. И чем ближе изображение в виду равнобедренного треугольника, тем ближе они будут друг к другу. Об этом 
репетитор по математике предупреждает ученика уже в 7 классе. Дети легко принимают за истину то, что кажется верным по рисунку. Так высоту, приходящую в кажущуюся середину стороны школьники легко принимают за медиану. В будущем, когда подготовка к ЕГЭ по математике поставит перед репетитором задачу научить ребенка решать номера С4, навыки изображения треугольников общего вида будут весьма полезны. Рисуйте равнобедренный треугольник только тогда, когда он дан в условии. Если имеется треугольник общего вида — изобразите его удлиненным в одну из сторон относительно основания высоты.
Репетитор по математике, А.Н. Колпаков.