Как рисовать тригонометрические функции

Как рисовать тригонометрические функции

Тема. Построение графиков тригонометрических функций

Формирование умений строить графики функций: у = Asin (kx + b ), у = Acos ( kx + b ), у = Atg ( kx + b ), у = Actg ( kx + b ).

И. Проверка домашнего задания

1. Один ученик воспроизводит решение упражнения № 24 (1-3).

2. Фронтальная беседа:

1) Назовите явления в природе, которые периодически повторяются.

2) Дайте определение периодической функции.

4) Найдите наименьший положительный период функций:

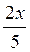
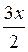
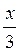
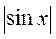
a ) y = cos ; б) y = sin ; в) у = tg ; г) у = .

5) периодическая функция у = С? Если да, то укажите период этой функции.

II. Построение графика функции у = sin х

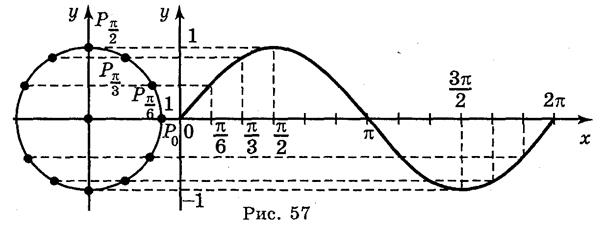
Для построения графика функции у = sin x воспользуемся единичным кругом. Построим единичный круг радиусом 1 см (2 клетки). Справа построим систему координат, как на рис. 57.

На ось ОХ нанесем точки ; π ; ; 2 π (соответственно 3 ячейки, 6 ячеек 9 ячеек, 12 ячеек). Разделим первую четверть единичного круга на три равные части и на столько же частей отрезок оси абсцисс. Перенесем значение синуса до соответствующих точек оси ОХ. Получим точки, которые надо соединить плавной линией. Затем разделим вторую, третью и четвертую четверть единичного круга также на три равные части и перенесем значение синуса до соответствующей точки оси ОХ. Последовательно соединив все полученные точки, получим график функции у = sin х на промежутке [0;π ].

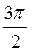
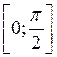
1. Постройте графики функций.

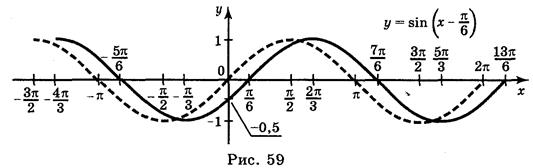
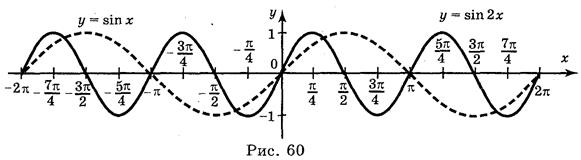
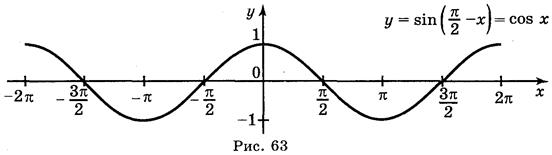
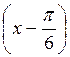
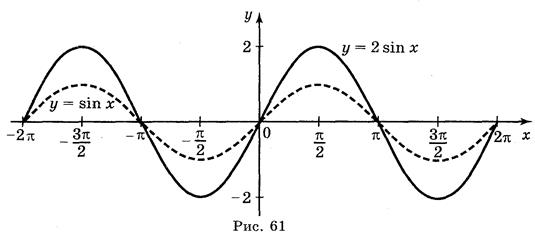
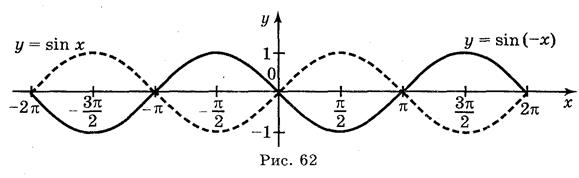
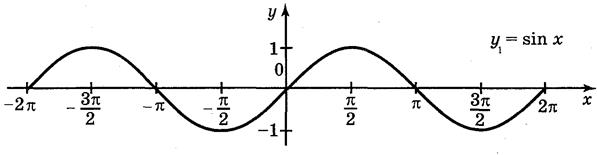
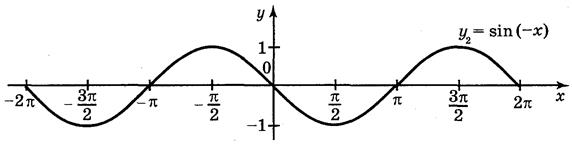
а) у = sin ; б) у = sin 2х; в) у = 2 sin х ; г) у = sin (-x).

Ответы: а) рис. 59; б) рис. 60; в) рис. 61; г) рис. 62.

1. Постройте графики функций:

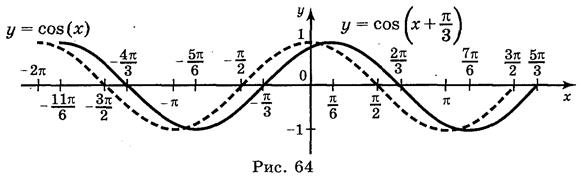
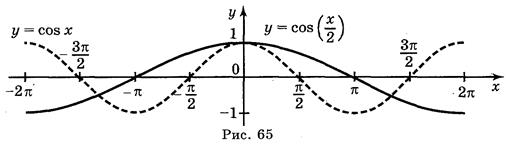
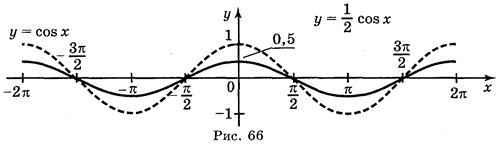
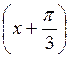
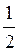
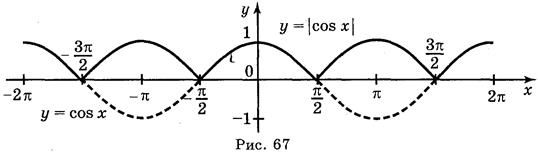
a ) y = cos ; б) y = cos ; в) y = cos х ; г ) у = | cos x |.

Ответ: а) рис. 64; б) рис. 65; в) рис. 66; г) рис. 67.

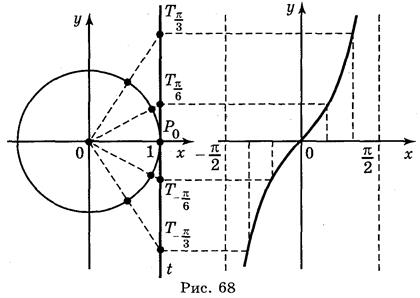
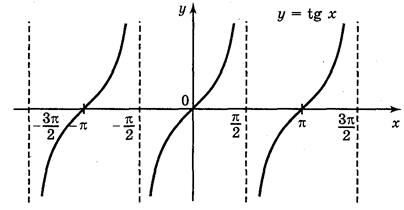
IV. Построение графика функции у = tg x

График функции у = tg x построим с помощью линии тангенсов на промежутке 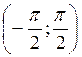, длина которого равна периоду π этой функции. Построим единичный круг радиусом 2 см (4 ячейки) и проведем линию тангенсов. Справа построим систему координат, как на рис. 68.

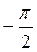
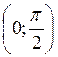
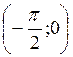
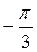
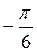
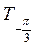
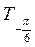
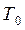
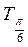
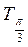
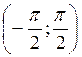
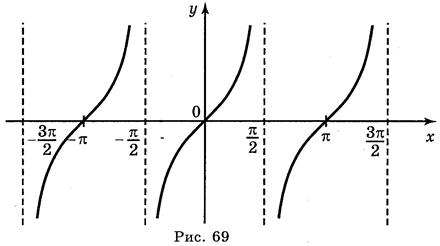
На ось ОХ нанесем точки ; (6 ячеек). Разделим первую и четвертую четверть окружности на 3 равные части и на столько же частей каждый из отрезков и . Найдем значения тангенсов чисел ; ; 0; ; с помощью линии тангенсов (ординаты точек ; ; ; ; линии тангенсов). Перенесем значения тангенсов до соответствующих точек оси ОХ. Последовательно соединив все полученные точки, получим график функции у = tg x на промежутке .

График функции у = tg x называется тангенсоїдою.

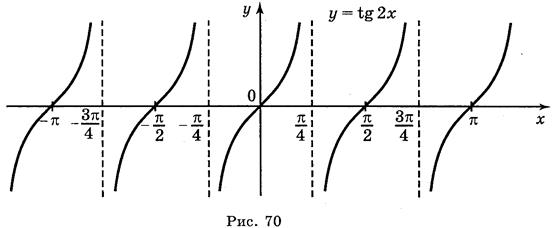
1. Постройте график функций

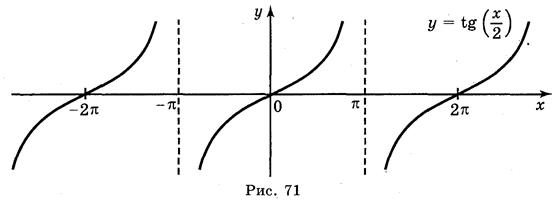
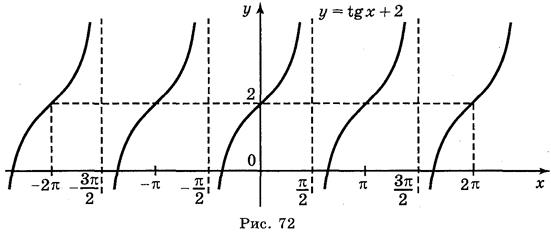
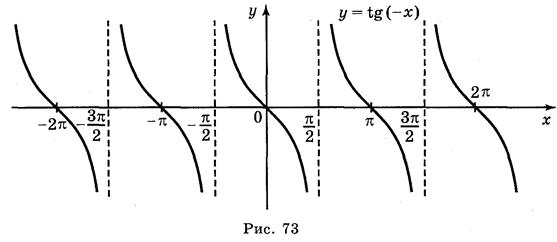
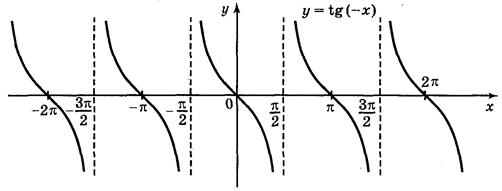
а) у = tg 2х; б) у = t g x ; в) у = tg x + 2; г) у = tg (-x).

Ответы: а) рис. 70; б) рис. 71; в) рис. 72; г) рис. 73.

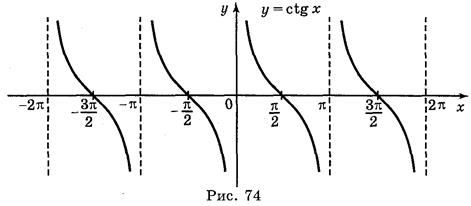
V. Построение графика функции у = ctg x

График функции у = ctg x легко получить, воспользовавшись формулой ctg x = tg 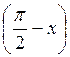и двумя геометрическими преобразованиями (рис. 74) симметрия относительно оси ΟΥ параллельный перенос вдоль оси ОХ на .

IV. Домашнее задание

Раздел И § 6. Вопросы и задания для повторения раздела И № 50-51. Упражнения № 28 (а-г).

Источник

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Синус и косинус угла на единичной окружности

Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:

С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что

ВС = АВ•sinα = 5•0,8 = 4

Если известно, что cosα = 0,6, то мы сможем найти и второй катет:

АС = АВ•cosα = 5•0,6 = 3

Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:

tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)

Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты х_А и у_А:

Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:

Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле

Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда

АВ = sinα•ОА = sinα•1 = sinα

С другой стороны, видно, что величина отрезка АВ равна координате у_А. Получается, что у_А = АВ = sinα, или

Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:

Учитывая, что ОА = 1, а длина ОВ равна координате х_А, мы получим следующее:

х_А = ОВ = cosα•ОА = cosα•1 = cosα

то есть координата х_А равна cos α:

Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.

Таким образом, нам удалось дать новое определение синусу и косинусу угла:

Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 1 I и II четверть

Источник

Тригонометрические функции

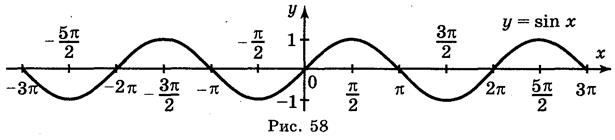
1. Начнем с построения графика функции y = sin x.

Вспомним, что у нас есть тригонометрический круг, на котором обозначены синусы и косинусы основных углов. Удобнее всего отметить на будущем графике точки, в которых значение синуса является рациональным числом.

Кроме того, значения синуса повторяются через полный круг или через целое число кругов, то есть

Это значит, что функция y = sin x является периодической. Мы уже построили уча-сток графика длиной 2π. А теперь мы как будто «копируем» этот участок и повторяем его с периодом 2π:

Синусоида построена.
Перечислим основные свойства функции y = sin x.

Перечислим основные свойства функции y = cos x.

Форма графиков функций синус и косинус, которые мы построили, очень характерна и хорошо знакома нам. Такой линией дети рисуют волны. Да, это и есть волны!

3. Перейдем к графику функции y = tg x.

Осталось только «скопировать» этот участок графика и повторить его с периодом π.

Перечислим свойства функции y = tg x.

5) Функция y = tg x возрастает при то есть на каждом участке, на котором она непрерывна.

4. График функции y = ctg x строится аналогично. Вот он:

5) Функция y = сtg x убывает при то есть на каждом участке, на котором она непрерывна.

Источник

Геометрия. Урок 1. Тригонометрия

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Тригонометрия в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

Тригонометрия: Тригонометрический круг

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.

Рассмотрим прямоугольный треугольник A O B :

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Основное тригонометрическое тождество

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

Тригонометрия: Таблица значений тригонометрических функций

0 °30 °45 °60 °90 °sin α01 22 23 21cos α13 22 21 20tg α03 313нетctg αнет313 30

Тригонометрия: градусы и радианы

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Тригонометрия: Формулы приведения

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Тригонометрия: Теорема синусов

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Тригонометрия: Расширенная теорема синусов

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Тригонометрия: Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с тригонометрией.

Тригонометрия: Тригонометрические уравнения

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

Источник

История тригонометрических функций

Самой первой тригонометрической функцией была хорда, соответствующая данной дуге. Для этой функции были построены первые тригонометрические таблицы (II в. до н. э.), нужные для астрономии.
Впервые в истории науки в период V-XII веков индийские математики и астрономы вместо полной хорды стали рассматривать половину хорды, которая соответствует современному понятию синуса. Величину половины хорды они назвали “архиджива”, что означало “половина тетивы лука”. Кроме sin x, индийцы рассматривали также величину 1 – cos x, которую они называли “комаджива”, и величину cos x – “котиджива”.
Понятие таких тригонометрических функций, как тангенс, котангенс, секанс и косеканс, определил совершенно строго, исходя из рассмотрения тригонометрического круга, иранский математик Абу-ль-Вефа. Современные названия этих функций были даны в период с XV по XVII век европейскими учеными. Так, термин “тангенс” с латинского “касательная” был введен в XV веке основателем тригонометрии в Европе Региомонтаном. В XVI веке Финк вводит термин “секанс”. В XVII веке помощник изобретателя десятичных логарифмов Бриггса ученый Гюнтер вводит название “косинус” и “котангенс”, причем приставка “ко” (co) обозначает дополнение (complementum).
Современные обозначения синуса и косинуса знаками sin x и cos x были впервые введены в 1739 году И. Бернулли в письме к петербургскому математику Л. Эйлеру. Последний пришел к выводу, что эти обозначения весьма удобны, и стал употреблять их в своих математических работах. Кроме того, Эйлер вводит следующие сокращенные обозначения тригонометрических функций угла x: tang x, cot x, sec x, cosec x. Далее Эйлер установил связь тригонометрических функций с показательными и дал правило для определения знаков функций в различных четвертях круга. Эйлер установил современную точку зрения на тригонометрические как функции числового аргумента.
В1770 г. появилось и удерживается до наших дней название Тригонометрические функции. Его ввел Г. С. Клюгель в работе “Аналитическая тригонометрия”.

Определение и графики тригонометрических функций

Величины углов (аргументы функций): α, x
Тригонометрические функции: sinα, cosα, tanα, cotα, secα, cscα
Множество действительных чисел: R
Координаты точки окружности: x, y

Радиус круга: r
Целые числа: k

1. Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.

2. К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс,котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.

3. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.

4. Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r:
sinα=y/r.
Поскольку r=1, то синус равен ординате точки M(x,y).

5. Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r:
cosα=x/r

6. Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
tanα=y/x,x≠0

7. Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
cotα=x/y,y≠0

8. Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y):
secα=r/x=1/x,x≠0

9. Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y):
cscα=r/y=1/y,y≠0

10. В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Синусом угла α называется отношение противолежащего катета к гипотенузе.
Косинусом угла α называется отношение прилежащего катета к гипотенузе.
Тангенсом угла α называется противолежащего катета к прилежащему.
Котангенсом угла α называется прилежащего катета к противолежащему.
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету.
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.

11. График функции синус
y=sinx, область определения: x∈R, область значений: −1≤sinx≤1

12. График функции косинус
y=cosx, область определения: x∈R, область значений: −1≤cosx≤1

13. График функции тангенс
y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞ Где применяется тригонометрия

Тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей. Следует отметить применение в таких областях как: астрономия, физика, природа, биология, музыка, медицина и многие другие.

Тригонометрия в астрономии:

Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.

Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.

Составленные Гиппархом таблицы положений Солнца и Луны позволили предвычислять моменты наступления затмений (с ошибкой 1—2 ч). Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии. Он повысил точность наблюдений, применив для наведения на светило крест нитей в угломерных инструментах — секстантах и квадрантах. Ученый составил огромный по тем временам каталог положений 850 звезд, разделив их по блеску на 6 степеней (звездных величин). Гиппарх ввел географические координаты — широту и долготу, и его можно считать основателем математической географии. (ок. 190 до н. э. — ок. 120 до н. э.)

Достижения Виета в тригонометрии
Полное решение задачи об определении всех элементов плоского или сферического треугольников по трем данным элементам, важные разложения sin пх и cos пх по степеням cos х и sinx. Знание формулы синусов и косинусов кратных дуг дало возможность Виету решить уравнение 45-й степени, предложенное математиком А. Рооменом; Виет показал, что решение этого уравнения сводится к разделению угла на 45 равных частей и что существуют 23 положительных корня этого уравнения. Виет решил задачу Аполлония с помощью линейки и циркуля.
Решение сферических треугольников- одна из задач астрономии Вычислять стороны и углы любого сферического треугольника по трем подходящим образом заданным сторонам или углам позволяют следующие теоремы: (теорема синусов) (теорема косинусов для углов) (теорема косинусов для сторон).

Тригонометрия в физике:

В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений.

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:

Где х — значение изменяющейся величины, t — время, А — амплитуда колебаний, ω — циклическая частота колебаний, — полная фаза колебаний, r — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде x’’ + ω²x = 0.

Тригонометрия в природе.

Впервые теория радуги была дана в 1637 году Рене Декартом. Он объяснил радугу, как явление, связанное с отражением и преломлением света в дождевых каплях.

Северное сияние Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.

Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы.

· Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения.

· К тому же в биологии используется такое понятие как синус сонный, синус каротидный и венозный или пещеристый синус.

Тригонометрия и тригонометрические функции в медицине и биологии.

· Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.

· Основной земной ритм – суточный.

· Модель биоритмов можно построить с помощью тригонометрических функций.

Тригонометрия в биологии

Какие биологические процессы связаны с тригонометрией?

· Биологические ритмы, биоритмы связаны с тригонометрией

Связь биоритмов с тригонометрией

· Модель биоритмов можно построить с помощью графиков тригонометрических функций. Для этого необходимо ввести дату рождения человека ( день, месяц, год ) и длительность прогноза

Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.

При полёте птицы траектория взмаха крыльев образует синусоиду.

Возникновение музыкальной гармонии

· Согласно дошедшим из древности преданиям, первыми, кто попытался сделать это, были Пифагор и его ученики.

· Частоты, соответствующие одной и той же ноте в первой, второй и т.д. октавах, относятся, как 1:2:4:8…

· диатоническая гамма 2:3:5

Тригонометрия в архитектуре

· Детская школа Гауди в Барселоне

· Страховая корпорация Swiss Re в Лондоне

· Феликс Кандела Ресторан в Лос-Манантиалесе

Значения тригонометрических функций

Ключевые слова: радиан, радианная мера угла, тригонометрическая окружность, знаки тригонометрических функций

Значит, можно написать следующие формулы перехода от градусного измерения к радианному:
=180рад

Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.

Источник