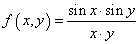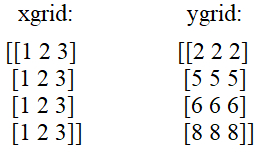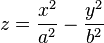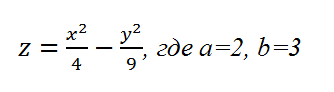Как рисовать трехмерный график
Как строить трехмерные графики
Следующим шагом мы с вами рассмотрим возможности построения трехмерных графиков в пакете matplotlib. Такая возможность появилась, начиная с версии 0.99, поэтому убедитесь, что ваш пакет поддерживает трехмерные графики.
Все дополнительные классы для работы в 3D находятся в модуле:
и вначале мы его импортируем в нашу программу наряду с самим пакетом matplotlib и numpy:
А, затем, создадим трехмерную систему координат:
При выполнении этой простой программы, мы в окне увидим три пространственные оси, которые можно вращать с помощью курсора мышки:
Того же самого результат можно добиться, используя параметр projection при создании системы координат:
Как именно создавать трехмерные оси, зависит от вашего выбора и удобства при написании конкретных программ. Я остановлюсь на втором способе.
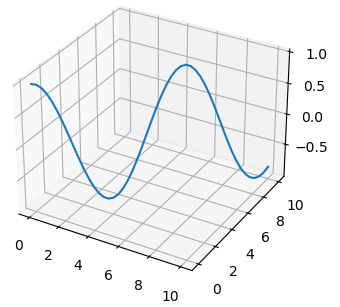
Начнем с самого простого варианта – функции plot() для рисования косинусоиды в трех измерениях:
То есть, мы здесь по координатам x, y выбираем одни и те же значения, а координата z (вертикаль) – это значение функции. Давайте подпишем оси, чтобы видеть, где какая расположена на этом графике:
Но то, что мы получили, это не совсем трехмерный график. Скорее, это двумерная косинусоида в трех измерениях. Давайте построим настоящее трехмерное изображение, например, вот такой функции:
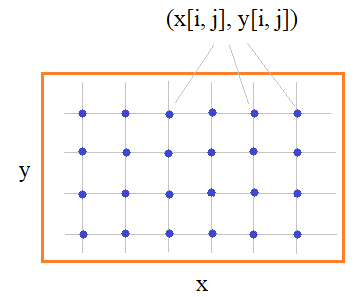
Первое, что нам здесь нужно сделать – это сформировать двумерную сетку координат по осям x и y:
То есть, должны быть сформированы двумерные массивы x, y, которые для текущей точки с индексами (i, j) возвращают ее координаты в плоскости xy.
Для регулярных сеток эти массивы можно сформировать следующим образом. Определим множество координат x (для столбцов) и y (для строк), например, так:
А, затем, используя функцию meshgrid() сформируем регулярную сетку на основе этих данных:
На выходе получим двумерные массивы со значениями:
То есть, смотрите, теперь для любой пары индексов (i, j) мы легко сможем получить координаты точки в плоскости xy:
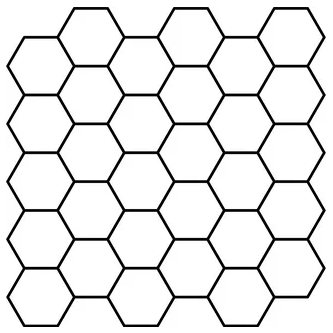
Но зачем было так все усложнять? Почему бы не использовать одномерные массивы x, y вместо двумерных xgrid, ygrid? Дело в том, что одномерные массивы, которые описывают расположение строк и столбов, могут формировать только регулярные сетки, то есть, прямоугольные. А что, если нужно сформировать гексагональную сетку, которая выглядит, следующим образом:
Здесь уже не получится обойтись указанными одномерными массивами, а нужно прописывать узлы двумерными массивами. Именно поэтому, в общем случае, и реализовано отображение через двумерные массивы трехмерных графиков.
Итак, давайте теперь построим полноценный трехмерный график синусоиды на регулярной сетке. Для этого мы сначала сформируем координаты узлов в плоскости xy:
А, затем, вычислим значения синусоиды в этих узлах:
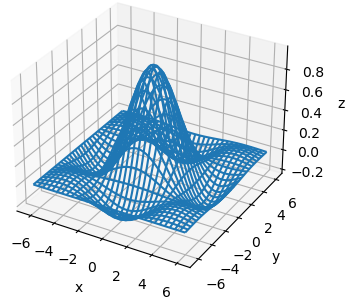
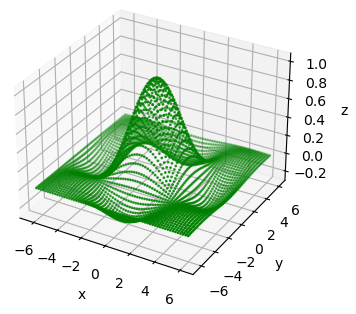
Если для вывода такого графика воспользоваться функцией plot_wireframe():
то результат будет следующий:
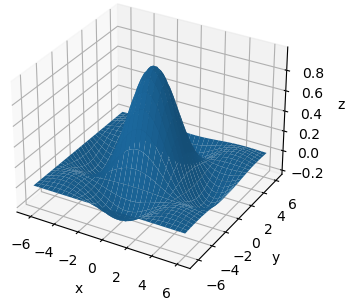
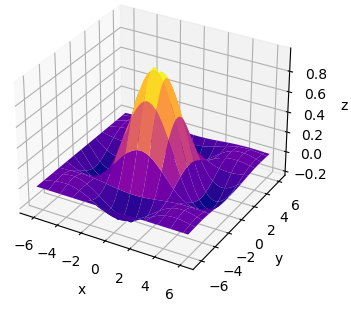
Как видите, мы получили полноценный каркасный трехмерный график синусоиды. Или же можно построить полноценную поверхность в виде синусоиды, используя функцию plot_surface():
Фактически, только этим две эти функции и отличаются друг от друга: первая строит 3D-каркас, а вторая 3D-поверхность.
У этих функций есть следующие параметры для настройки внешнего вида графика:
Например, если установить параметры:
то получим следующий вид нашей синусоиды:
В заключение этого занятия приведу пример построения этого же графика набором точек, используя функцию scatter():
Увидим следующий результат:
Вот так в базовом варианте можно выполнять построения трехмерных графиков в пакете matplotlib. Этой информации достаточно для большинства прикладных задач. Ну а если потребуется реализовать что-то особенное, тогда прямой путь к документации:
Видео по теме
#1. Установка пакета и основные возможности
#2. Функция plot для построения и оформления двумерных графиков
#3. Отображение нескольких координатных осей в одном окне
#4. Граничные значения осей и локаторы для расположения меток на них
#5. Настраиваем формат отображения меток у координатных осей
#6. Делаем логарифмический масштаб у координатных осей
#7. Размещаем стандартные текстовые элементы на графике
#8. Добавляем легенду и рисуем геометрические фигуры на графиках
#9. Рисуем ступенчатые, стековые, stem и точечные графики
#10. Рисуем гистограммы, столбчатые и круговые диаграммы
#11. Показ изображений и цветовых сеток
#12. Как строить трехмерные графики
#13. Рисуем линии уровня функциями contour, contourf и tricontour, tricontourf
#14. Создаем анимацию графиков Классы FuncAnimation и ArtistAnimation
© 2021 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта
3-Мерные графики в Python с использованием Matplotlib
Как и 2-мерные графики, вы также можете создавать 3-мерные графики в Python с помощью matplotlib. В этом уроке мы узнаем, как построить трехмерный график
Как и 2-мерные графики, вы также можете создавать 3-мерные графики в Python с помощью matplotlib. В этом уроке мы узнаем, как строить трехмерные графики с помощью matplotlib.
Как построить трехмерные графики в Python?
Мы будем использовать инструментарий mplot3d вместе с библиотекой matplotlib . Инструментарий mplot3d построен на базе библиотеки matplotlib, чтобы упростить создание трехмерных графиков.
Так что без дальнейших задержек, давайте начнем!
1. Импортируйте необходимые модули
2. Создайте трехмерные оси
Теперь, когда у нас есть топоры, давайте попробуем что-нибудь придумать. При построении графика нам нужно убедиться,что мы предоставляем значения для всех трех осей ( x, y и z).
В следующих разделах мы узнаем, как сделать спираль, используя синусоидальные функции(синус и косинус).
Перед этим мы узнаем, как добавить заголовок к сюжету.
3. Добавление заголовка к сюжету
Вы можете добавить заголовок к своим участкам с помощью метода set_title():
Чтобы увидеть приведенную выше строку кода в действии, выполните следующие действия:
4. Создайте спираль
Для создания спирали мы будем использовать функцию синуса вдоль оси x и функцию косинуса вдоль оси y.
Точки данных для спирали могут быть сгенерированы следующим образом:
Здесь функция np.linspace дает 1000 точек с равным расстоянием между 0 и 15.
Полный код выглядит следующим образом:
5. Измените угол обзора
Трехмерные графики выглядят по-разному в зависимости от угла обзора. Вы можете изменить угол обзора трехмерных графиков с помощью метода view_init():
Полный код приведен ниже:
Здесь мы упоминаем два аргумента: высоту и угол наклона осей(в градусах).
Давайте попробуем под другим углом.
6. Построение каркаса из проволоки
Вы можете построить трехмерный каркас с помощью метода plot_wireframe (), как показано в приведенном ниже примере:
Здесь функция np.meshgrid создает матрицы координат из векторов координат.
Аналогично, вы также можете создать поверхностный участок. Давайте узнаем, как это сделать, в следующем разделе.
7. Создайте поверхностный участок
Мы можем создать поверхностный график с теми же данными, что и выше. Чтобы создать трехмерный график поверхности, мы будем использовать метод plot_surface ().
Здесь следующие аргументы означают следующее:
| шаг | Шаг строки массива (размер шага) |
| cstrike | Шаг столбца массива (размер шага) |
| лагерь | Цветовая карта для участков поверхности. |
Вывод
В этом уроке речь шла о трехмерных графиках на Python. Мы научились строить трехмерные оси вместе с точками данных. Чтобы узнать больше о трехмерных фигурах в mplot3d, обратитесь к их официальной документации.
Многомерные графики в Python — от трёхмерных и до шестимерных
Введение
Визуализация — важная часть анализа данных, а способность посмотреть на несколько измерений одновременно эту задачу облегчает. В туториале мы будем рисовать графики вплоть до 6 измерений.
Plotly — это питоновская библиотека с открытым исходным кодом для разнообразной визуализации, которая предлагает гораздо больше настроек, чем известные matplotlib и seaborn. Модуль устанавливается как обычно — pip install plotly. Его мы и будем использовать для рисования графиков.
Давайте подготовим данные
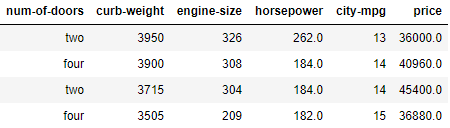
Для визуализации мы используем простые данные об автомобилях от UCI (Калифорнийский университет в Ирвине — прим. перев.), которые представляют собой 26 характеристик для 205 машин (26 столбцов на 205 строк). Для визуализации шести измерений мы возьмём такие шесть параметров.
Загрузим данные из CSV с помощью pandas.
Теперь, подготовившись, начнем с двух измерений.
Двухмерная диаграмма рассеяния
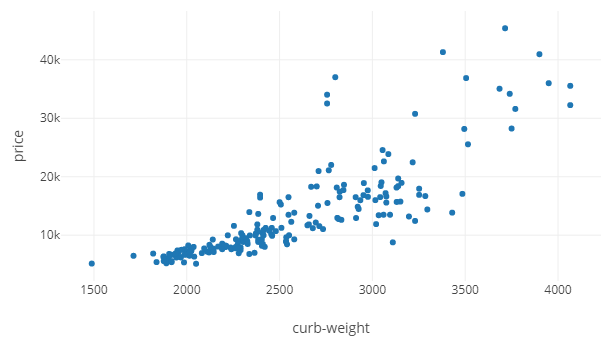
Диаграмма рассеяния — весьма простой и распространенный график. Из 6 параметров, price и curb-weight используются ниже как Y и X соответственно.
В plotly процесс немного отличен от аналогичного в Matplotlib. Мы должны создать layout и figure, передав их в функцию offline.plot, после чего результат будет сохранён в HTML файл в текущей рабочей директории. Вот скриншот того, что получится. В конце статьи будет ссылка на GitHub репозиторий с готовыми интерактивными HTML-графиками.
Диаграмма рассеяния в 3D
Мы можем добавить третий параметр horsepower (количество лошадиных сил) на ось Z. Plotly предоставляет функцию Scatter3D для построения интерактивных трёхмерных графиков.
Вместо того чтобы вставлять код сюда каждый раз, я добавлял его в репозиторий.
(Удобнее всего смотреть релевантный код в соседней вкладке параллельно со чтением — прим. перев.)
Добавление четвёртого измерения
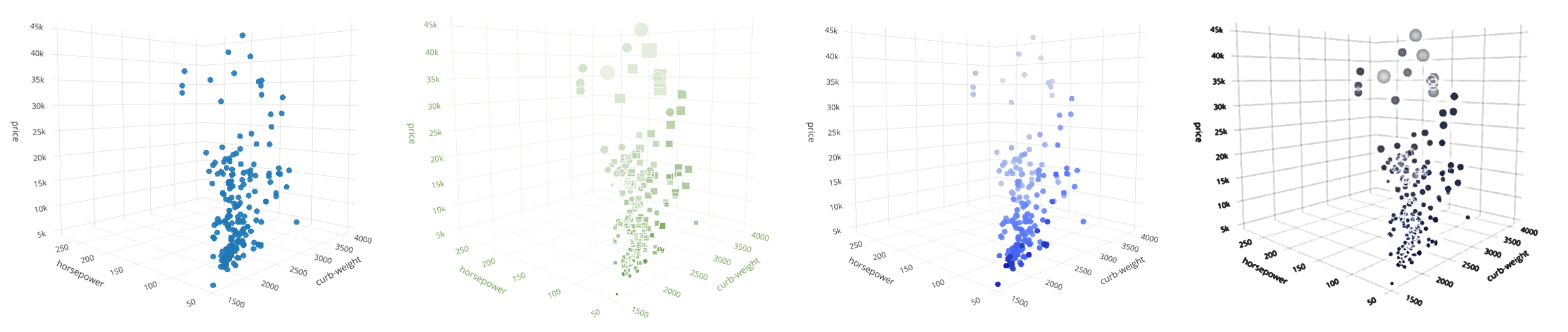
Мы знаем, что использовать больше трёх измерений напрямую нельзя, но есть обходной путь: мы можем эмулировать глубину для визуализации более высоких измерений с помощью цвета, размера или формы.
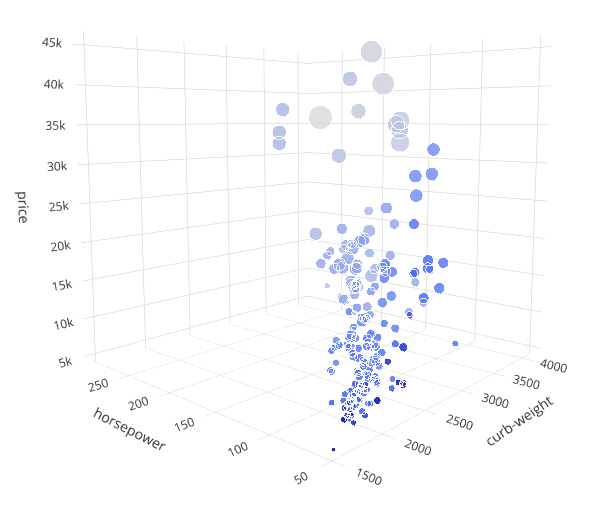
Здесь, наряду с тремя предыдущими характеристиками, мы будем использовать пробег в городских условиях — city-mpg как четвертое измерение, за которое будет отвечать параметр markercolor функции Scatter3D. Более светлый оттенок маркера будет означать меньший пробег.
Сразу же бросается в глаза, что чем выше цена, количество лошадей и масса, тем меньше будет пробег.
Добавление пятого измерения
Размер маркера можно использовать для визуализации 5-го измерения. Мы используем характеристику engine-size (размер двигателя) для параметра markersize функции Scatter3D.
Наблюдения: размер двигателя связан с некоторыми из предыдущих параметров. Чем выше цена, тем больше двигатель. Ра́вно как и: ниже пробег — больше двигатель.
Добавление шестого измерения
Форма маркера отлично подходит для визуализации категорий. Plotly даёт на выбор 10 различных фигур для 3D графика (звёздочка, круг, квадрат и т.д.). Таким образом, в качестве формы можно показать до 10 различных значений.
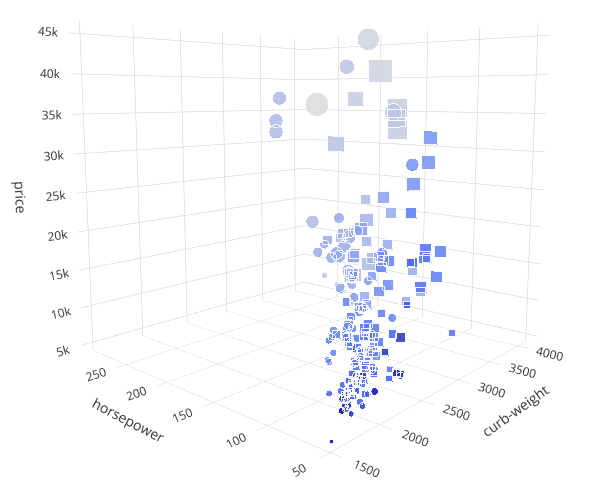
У нас есть характеристика num-of-doors, которая содержит целые числа — количество дверей (2 или 4). Преобразуем эти значения в фигуры: квадрат для 4 дверей, круг для 2 дверей. Используется параметр markersymbol функции Scatter3D.
Наблюдения: такое чувство, что у всех самых дешёвых машин по 4 двери (круги). Продолжая изучать график, можно будет сделать больше предположений и выводов.
6D график с формой маркера в качестве шестого измерения (количество дверей)
Можем ли мы добавить больше измерений?
Конечно можем! У маркеров есть больше свойств, таких как непрозрачность и градиенты, которые можно задействовать. Но чем больше измерений мы добавляем, тем труднее удержать их все в голове.
Исходный код
Код на Python и интерактивные графики для всех фигур доступны на GitHub здесь.
Построить трехмерный график по точкам
Трехмерные графики функции
Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3 ).
Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3 ).
Принципы и способы построения графика функции
Прикладное применение графика функции
Построить пирамиду ABCD по координатам можно здесь.
Введение
Визуализация — важная часть анализа данных, а способность посмотреть на несколько измерений одновременно эту задачу облегчает. В туториале мы будем рисовать графики вплоть до 6 измерений.
Plotly — это питоновская библиотека с открытым исходным кодом для разнообразной визуализации, которая предлагает гораздо больше настроек, чем известные matplotlib и seaborn. Модуль устанавливается как обычно — pip install plotly. Его мы и будем использовать для рисования графиков.
Давайте подготовим данные
Для визуализации мы используем простые данные об автомобилях от UCI (Калифорнийский университет в Ирвине — прим. перев.), которые представляют собой 26 характеристик для 205 машин (26 столбцов на 205 строк). Для визуализации шести измерений мы возьмём такие шесть параметров.
Загрузим данные из CSV с помощью pandas.
Теперь, подготовившись, начнем с двух измерений.
Двухмерная диаграмма рассеяния
Диаграмма рассеяния — весьма простой и распространенный график. Из 6 параметров, price и curb-weight используются ниже как Y и X соответственно.
В plotly процесс немного отличен от аналогичного в Matplotlib. Мы должны создать layout и figure, передав их в функцию offline.plot, после чего результат будет сохранён в HTML файл в текущей рабочей директории. Вот скриншот того, что получится. В конце статьи будет ссылка на GitHub репозиторий с готовыми интерактивными HTML-графиками.
Диаграмма рассеяния в 3D
Мы можем добавить третий параметр horsepower (количество лошадиных сил) на ось Z. Plotly предоставляет функцию Scatter3D для построения интерактивных трёхмерных графиков.
Вместо того чтобы вставлять код сюда каждый раз, я добавлял его в репозиторий.
(Удобнее всего смотреть релевантный код в соседней вкладке параллельно со чтением — прим. перев.)
Добавление четвёртого измерения
Мы знаем, что использовать больше трёх измерений напрямую нельзя, но есть обходной путь: мы можем эмулировать глубину для визуализации более высоких измерений с помощью цвета, размера или формы.
Здесь, наряду с тремя предыдущими характеристиками, мы будем использовать пробег в городских условиях — city-mpg как четвертое измерение, за которое будет отвечать параметр markercolor функции Scatter3D. Более светлый оттенок маркера будет означать меньший пробег.
Сразу же бросается в глаза, что чем выше цена, количество лошадей и масса, тем меньше будет пробег.
Добавление пятого измерения
Размер маркера можно использовать для визуализации 5-го измерения. Мы используем характеристику engine-size (размер двигателя) для параметра markersize функции Scatter3D.
Наблюдения: размер двигателя связан с некоторыми из предыдущих параметров. Чем выше цена, тем больше двигатель. Ра́вно как и: ниже пробег — больше двигатель.
Добавление шестого измерения
Форма маркера отлично подходит для визуализации категорий. Plotly даёт на выбор 10 различных фигур для 3D графика (звёздочка, круг, квадрат и т.д.). Таким образом, в качестве формы можно показать до 10 различных значений.
У нас есть характеристика num-of-doors, которая содержит целые числа — количество дверей (2 или 4). Преобразуем эти значения в фигуры: квадрат для 4 дверей, круг для 2 дверей. Используется параметр markersymbol функции Scatter3D.
Наблюдения: такое чувство, что у всех самых дешёвых машин по 4 двери (круги). Продолжая изучать график, можно будет сделать больше предположений и выводов.
6D график с формой маркера в качестве шестого измерения (количество дверей)
Можем ли мы добавить больше измерений?
Конечно можем! У маркеров есть больше свойств, таких как непрозрачность и градиенты, которые можно задействовать. Но чем больше измерений мы добавляем, тем труднее удержать их все в голове.
Исходный код
Код на Python и интерактивные графики для всех фигур доступны на GitHub здесь.
В продолжении темы о графиках функций в Excel расскажу о построении трехмерных графиков.
Трехмерный график функции — это график в трех измерениях. Соответственно каждая точка графика будет иметь три координаты (x, y. z).
Построим график функции, называемый гиперболический параболоид, в Excel.
Уравнение гиперболического параболоида (общий вид):
где x, y, z — переменные; a, b — константы.
Рассмотрим конкретный случай:
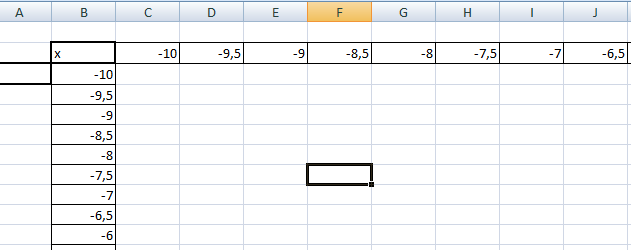
Как и для построения графика функции на плоскости нам потребуется таблица, на основании которой график и будет построен.
по горизонтали — значения х, по вертикали — значения у.
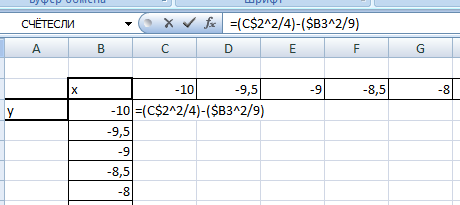
Значения z вычисляются по формуле (см. выше). Запишем формулу для вычисления z, где x=10, y = 10, a=2, b=3.
Используя маркер автозаполнения, копируем формулу для всех значений x и y.
Получим таблицу, в которой каждой паре (x, y) соответствует координата z.
Выделяем диапазон ячеек со значениями z, выбираем ВСТАВКА — ДРУГИЕ ДИАГРАММЫ — ПОВЕРХНОСТЬ
3D моделирование в Python
Допустим, вам потребовалось на языке программирования python, построить трёхмерную модель некоторого объекта, затем визуализировать его, или подготовить файл для печати на 3D принтере. Существует несколько библиотек, помогающих в решении этих задач. Поговорим о том, как строить трёхмерные модели из точек, граней и примитивов в python. Как выполнять элементарные приемы 3D моделирования: перемещение, поворот, объединение, вычитание и другие.
Примеры кода можно найти в репозитории на GitHub.
Docker для исполнения примеров Pymesh:
sudo sh get-docker.sh
Компилятор g++ для PyTorch3d:
sudo apt install g++
Клонирование репозитория и установка библиотек:
git clone https://github.com/format37/python3d.git
pip install «git+https://github.com/facebookresearch/pytorch3d.git»
sudo apt-get install openscad
Numpy-stl: Обзор библиотеки
Изображение из Википедии
Если вы не знакомы с Jupyter notebook
Вершины пирамиды
Несмотря на то, что пока описаны только вершины, уже можно взглянуть как будет выглядеть модель, если соединить их треугольниками:
Изоповерхность пирамиды
Выглядит так, будто грани уже существуют. Но пока у нас есть только вершины. Чтобы сформировать stl файл, опишем грани, что можно сделать вручную, или предоставить эту работу функции spatial.ConvexHull из библиотеки scipy
В результате, массив faces содержит описание граней:
Например, последняя грань содержит числа 3, 1, 0. Значит грань собрана из точек 0-го, 1-го и 3-го элементов массива vertices:
Принцип описания граней через позиции вершин
Грани пирамиды
Как видно из рисунка, одна грань пирамиды оказалась перевернута. В последующих примерах, при построении фракталов, метод ConvexHull применяться не будет, так как он располагает точки грани в произвольном порядке, что приводит к переворачиванию некоторых граней.
Для просмотра stl файлов разработано довольно много программ. Одна из них называется Blender, доступна для скачивания и не требует оплаты за использование
Снимок экрана. Blender: numpy_stl_example_02.stl
Метод spatial.ConvexHull предназначен для вычисления выпуклой оболочки и хорошо справляется с пирамидой и кубом. Но в объектах, имеющих впадины, часть точек будет потеряна и при сборке stl произойдет ошибка из-за несоответствия количества граней количеству точек.
Это хорошо видно на примере в двух измерениях: numpy_stl_example_03.ipynb
В hull.simplices содержится описание граней:
Отобразим вершины и грани на графике:
Центральные точки не связаны с гранями
Для таких случаев придется найти альтернативу ConvexHull, или описать грани вручную:
Добавлено две грани: одна для нижней точки, одна для верхней
Numpy-stl: Построение фрактала
Пришло время построить фрактал. В numpy-stl нет функции булева вычитания. Для построения фрактала Menger Sponge пойдем от обратного. В нашем распоряжении два метода:
Построение элементарного mesh куба. Назовем его voxel.
Объединение нескольких voxel в единый mesh.
Построим фрактал из кубиков, как из конструктора.
Описание логики построения фрактала
Найдем сторону вокселя на глубинах 1 и 2. Упростим задачу, свернув фрактал с 3-х до 1-мерного случая:
Если фрактал второго уровня, длина стороны куба составит 1/(3**2) или 1/9. Составим набор кубов так, чтобы своим расположением они заполнили исходный куб. Получится воксельный куб. Вычислим области отверстий. Исключим воксели, которые входят в области отверстий. В завершение, объединим оставшиеся воксели в один объект и сохраним.
Numpy-stl: Рендеринг изображения
Для рендеринга, в функцию вывода plot_mesh, будем передавать mesh, загруженный из stl файла.
PyMesh: Обзор библиотеки
К сожалению, библиотека PyMesh не установилась у меня ни через менеджер пакетов PIP (несмотря на упоминание этого способа в документации), ни через Anaconda. Есть два способа установки.
Следуя инструкции, собрать из исходников.
Используя Docker контейнер. Выберем этот вариант, как более интересный. Запуск контейнера будет инициирован с параметрами. При помощи параметров запуска смонтируем в контейнер папку скриптов. Передадим необходимые параметры в скрипт. После завершения работы скрипта, контейнер будет удален. Если Docker вы уже установили следуя инструкции в начале статьи, более ничего устанавливать не нужно.
Если Docker вам не подходит, скомпилируйте PyMesh, следуя инструкции в документации. Такой вариант тоже будет работать.
Начнем с простого куба. В папке pymesh_examples находится скрипт pymesh_example_01.py. В дальнейшем, контейнер будет брать файлы именно из этой папки.
Из корня проекта запустим контейнер:
Что тут происходит?
Запускается контейнер pymesh. При первом запуске будет загружен образ, это займёт некоторое время.
Папка pymesh_examples монтируется в контейнер
В контейнере запускается python скрипт /pymesh_examples/pymesh_example_01.py
Импортируется библиотека pymesh
функция generate_box_mesh генерирует куб на основании двух противоположных вершин в точках [0,0,0] и [1,1,1]
функция save_mesh сохраняет объект в stl файл.
После исполнения, в папке pymesh_examples появляется файл pymesh_example_01.stl
Квадратное отверстие сделаем при помощи булева вычитания. Строим параллелепипед и вычитаем его из основного куба.
Снимок экрана. Blender: pymesh_example_02.stl
Здесь boolean применяется не только для вычитания. Всего доступно 4 операции:
Difference: A∖B (два последних примера)
Symmetric difference: A XOR B (изображение не представлено)
Иллюстрация применения операции boolean на сфере и кубе
Чтобы лучше понять как перемещать и вращать объект, бывает удобно временно заменить операцию Difference на Union.
Сделаем второе отверстие, переместим и повернем его.
В этом скрипте добавлены функции перемещения и поворота. При перемещении создается новый mesh объект на основании измененных вершин и граней исходного объекта. Для поворота, сначала при помощи класса Quaternion, описывается поворот, а затем, аналогично случаю с перемещением, используется создание нового, повернутого объекта, на основании вершин и граней исходного объекта, а также описания поворота.
О кватернионах есть довольно подробная статья:
В результате исполнения скрипта, получается куб с двумя пересекающимися отверстиями:
Снимок экрана. Blender: pymesh_example_03.stl
Перечисленных инструментов достаточно для построения фрактала.
PyMesh: Построение фрактала
В этом скрипте добавлен входящий параметр для передачи глубины вычисления фрактала. Для каждой глубины создается параллелепипед, который затем дважды копируется, поворачивается и смещается. Получается всего 3 параллелепипеда, которые вычитаются из основного куба. По одному на каждую грань. Операция повторяется x и y раз, чтобы заполнить все строки и колонки грани. Проверка на вычитание из пустого пространства не выполняется.
На этот раз при запуске необходимо явно указать глубину фрактала:
Исполняться он будет 5-15 минут. После исполнения, в папке pymesh_examples появляется stl файл:
Снимок экрана. Blender: pymesh_example_04_3.stl Если запросить фрактал 4-го уровня
Построение займет около 4-х часов, а размер файла составит 73 мб:
Снимок экрана. Blender: pymesh_example_04_4.stl
PyMesh: Рендеринг изображения
Mesh мы уже поворачивали, на этот раз повернём камеру.
Один из кадров анимации Показать анимацию
PyTorch3d: Обзор библиотеки
В примере ниже, сразу на устройстве описываем вершины, копируем их с устройства на хост. На основании вершин вычисляем грани. Сохраняем объект. Файл в формате obj можно импортировать в blender:
Снимок экрана. Blender: pytorch3d_example_01.obj
Обратите внимание на команду verts.cpu().numpy()
Вершины копируются с устройства на хост. Если вы работаете с GPU, каждое копирование будет замедлять работу алгоритма. В планировании архитектуры программы, количество операций копирования между хостом и устройством, по возможности, лучше свести к минимуму. Например, изначально имея на хосте список вершин, можно вычислить грани, не прибегая к копированию вершин с устройства на хост, как это будет сделано в следующем примере.
PyTorch3d: Построение фрактала
Использование GPU даёт некоторый прирост производительности.
В этом скрипте объявляем вершины минимального для указанной глубины вокселя. По знакомому из прошлого примера алгоритму вычисляем координаты отверстий в двух измерениях. Заполняем первичный куб вокселями, которые не попадают в пределы отверстий.
Cкорость расчета увеличилась на порядок, что позволило примерно за 5 часов построить фрактал 5 уровня:
Снимок экрана. Blender Menger Sponge 5 lvl
Размер stl файла составил 1.9 ГБ. При построении фрактала 5-го уровня, программа останавливалась из-за переполнения памяти видеокарты. Пришлось сборку объекта выполнять пакетами. Создавалось по 10 слоев “двумерных” фракталов, затем они присоединялись к основному объекту, до тех пор, пока не построился полный фрактал.
PyTorch3d: Рендеринг изображения
Помимо plotly визуализаций, pytorch3d отдельно выделяет рендеринг и подход нему тут довольно основательный, с текстурами и шейдерами.
SolidPython: Обзор библиотеки
SolidPython Самая богатая методами моделирования библиотека, среди перечисленных. 3D сцена описывается на python, в формате, очень похожем на openscad, генерируется openscad код, который пишется в scad файл и далее его можно редактировать в openscad или сразу сохранить в stl.
Снимок экрана. Openscad: solidpython_example_01.scad
solidpython удобно отлаживать. С одной стороны экрана открыт scad файл, с другой jupyter notebook. При исполнении scad_render_to_file картинка в openscad автоматически обновляется.
Если нужен stl, openscad умеет рендерить файлы этого формата через команды консоли. Пример вызова из jupyter notebook:
Снимок экрана. Blender: solidpython_example_01.stl
Общий принцип такой: Любая функция возвращает объект. Если над объектом необходимо произвести некоторое действие, объект (или список объектов) передается в круглых скобках после вызова соответствующей функции.
Тут разрешение регулируется параметром slices.
Снимок экрана. Openscad: solidpython_example_02.scad
SolidPython: Построение фрактала
SolidPython: Рендеринг изображения
Сформируем серию изображений последней сцены, поворачивая камеру в каждом изображении.
Кроме того, solidpython предлагает формирование анимации средствами openscad. В документации об этом есть небольшой раздел с примером.
Напоследок рассмотрим код, использованный для построения сцены из заголовка статьи.
Сравнение библиотек
Сравнение производительности не совсем объективно, так как имеются значительные различия в алгоритмах. В Pymesh и SolidPython применялось вычитание, тогда как в Numpy-stl и Pytorch3d объединение mesh.
(Время вычисления фрактала 3-го уровня, в секунду)