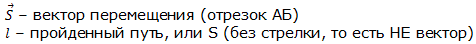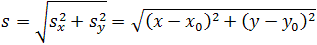Как рисовать траекторию движения

Траектория движения тела

Траектория представляет собой своеобразный «след», который оставляет за собой движущееся тело в данной системе отсчета. Она позволяет наблюдателю этой системы отсчета увидеть все точки, которые последовательно проходило тело во время движения. Например, железнодорожный путь указывает траекторию движения поезда, автомобильное шоссе – траекторию движения автомашин. След, оставшийся в небе за летящим самолетом, «рисует» траекторию самолета, лыжня – траекторию лыжника, а любой текст, написанный на листе бумаги – траекторию кончика карандаша или ручки.

Траектория тела в разных системах отсчета

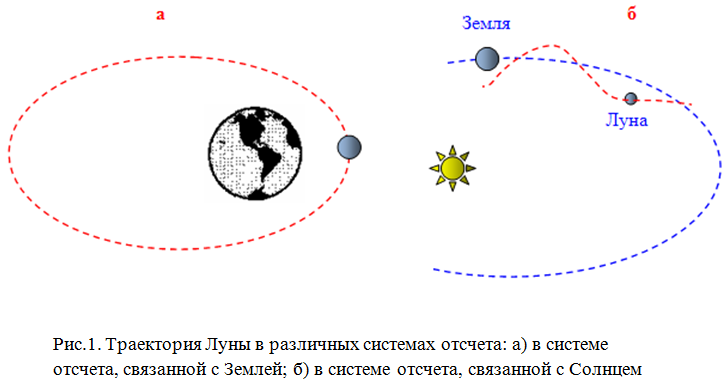
Следует отметить, что траектории движения одного и того же тела в разных системах отсчета могут быть различными. Например, в системе отсчета, связанной с Землей, траектория движения искусственного спутника вокруг Земли – окружность, а в системе отсчета, связанной с Солнцем, — винтовая линия или спираль (рис.1).

В зависимости от формы траектории механические движения делятся на прямолинейные (траектория – прямая линия) (рис.2, а) и криволинейные (траектория – кривая линия) (рис.2, б).

Определение уравнения траектории движения тела является одной из задач механики.

Примеры решения задач по теме «Траектория»

б) в системе отсчета, связанной с рамой, траектория точки обода вращающегося колеса – окружность, так как точка обода совершает вращательное движение относительно оси, закрепленной на раме;

в) в системе отсчета, связанной с землей, траектория точки обода вращающегося колеса – циклоида, потому что точка одновременно совершает поступательное и вращательное движения; длина дуги циклоиды равна длине окружности обода колеса.

Источник

Траектория

Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.

Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.

Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.

Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.

Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.

Вектор перемещения

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.

Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.

Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).

Рис. 1.1. Вектор перемещения и пройденный путь.

Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.

Правило сложения векторов

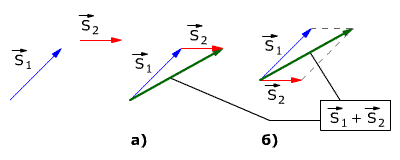
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).

Рис. 1.2. Сложение векторов перемещений.

На рис 1.2 показаны правила сложения векторов S1 и S2:

а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма

Проекции вектора перемещения

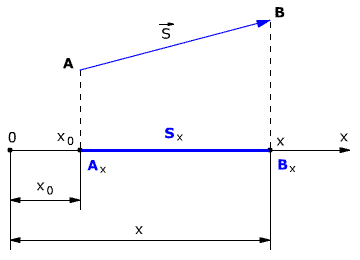
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения 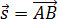(см.рис. 1.3).

Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно А_x и В_x. Длина отрезка А_xВ_x на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть

Рис. 1.3. Проекция вектора перемещения.

Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть

Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:

Здесь x₀, y₀, z₀ — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).

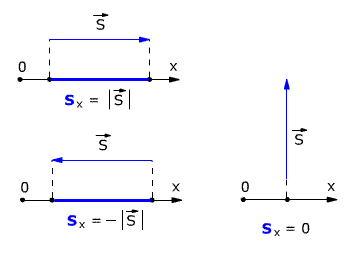
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).

Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).

Рис. 1.4. Модули проекции вектора перемещения.

Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.

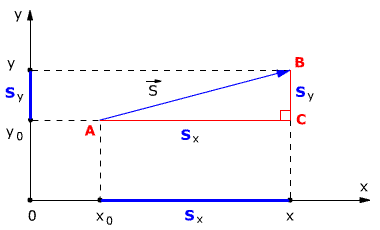
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х₀ и у₀, то есть А(х₀, у₀). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.

Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).

Рис. 1.5. Движение тела на плоскости.

Определим проекции вектора перемещения на осях ОХ и OY:

На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как

По теореме Пифагора

Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:

Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.

Источник

Как нарисовать движение: 16 лучших приемов

Бывший интерн Walt Disney Animation и сотрудница Sony Pictures Animation Бриттани Майерс (Brittany Myers) рассказала, как придать персонажам выразительности. Мы перессказали главное и немного дополнили материал.

Художники не просто рисуют героев, они стараются выражать идеи и рассказывать истории. Для этого очень важно думать не только о внешности персонажей, но и об их жестах и движениях. Вот несколько базовых советов о том, как сделать героев более выразительными.

Совет 1. Рисуйте линии действия

Прямая или изогнутая линия станут основой для передачи движения

Движение легко передать одной линией. Это линия действия. Она может быть как прямой, так и изогнутой; эти линии создают разные ощущения движения. Прямая линия, как правило, очень быстрая и направленная, а изогнутая линия создает более изящное настроение. Однако следует избегать идеально ровной вертикальной линии действия — она может сделать рисунок статичным.

Совет 2. Покажите, о чем думает персонаж

У всего есть причина. Можно ли предположить, почему девочка на картинке делает те или иные вещи? Видно ли это по рисунку?

Герои мультиков и фильмов кажутся нам настоящими. Точно так же стоит думать о своих персонажах — как о личностях с собственным сознанием, характером и желаниями. Если персонаж на рисунке движется или делает что-либо, у него должна быть причина для этого.

Не важно, что это за действие: бег или малозаметный жест вроде накручивания на палец пряди волос — у изображаемого персонажа, скорее всего, будет сознательная или бессознательная причина делать это. Если вы будете помнить об этом, то сможете создать более интересный и гармоничный образ.

Совет 3. Сочетайте прямые и изогнутые линии

Контрасты — хороший способ оживить рисунок. Их можно найти не только в цвете, масштабе или тоне, но и в характере линий.

Контраст прямых и изогнутых линий является важнейшим элементом дизайна. Ваш скетч состоит только из прямых линий? Он может получиться слишком напряженным. Изображению, состоящему в основном изогнутых линий, будет не хватать структуры.

Изогнутые линии используются, как правило, чтобы намекнуть на более чувственную часть фигуры, а прямые — для изображения статичных и массивных элементов. Например, сравните, как на примере выше прямой линией изображают спину персонажа, а мягкими изогнутыми линиями — живот.

Совет 4. Тренируйтесь. Рисуйте наброски

Рисование в классе, по фото и из жизни «качают» разные навыки и по разному помогают понять форму.

Выйдите на улицу и порисуйте. Рисование из жизни — чрезвычайно полезный инструмент наблюдения. Не важно, где делаете эскизы — в классе или в местном кафе. Изучая людей вокруг, вы научитесь рисовать фигуру человека и его настроение.

Хорошая идея сходить на занятия по рисованию с живой натуры. Как правило, они включают в себя как длинные, так и короткие наброски. Более длительные (10-15 мин) позволяют улавливать детали и изучать анатомию человека, в то время как быстрые (2-5 мин) больше подходят для изучения методики изображения жестов.

Прим. ред. В этом видео известный художник и аниматор Стефан Сильвер рассказывает, чем руководствуется в набросках из жизни.

Совет 5. Снова тренируйтесь. Рисуйте жесты

Жест можно набросать за короткий промежуток времени. Не нужно учитывать все нюансы — главное передать позу.

Изображение жеста — быстрый способ уловить фигуру «в общем». Подобные наблюдательные рисунки часто выполняются за очень короткий промежуток времени — на занятиях по рисованию с живой натуры модель может позировать лишь 30 секунд, чтобы художник мог зафиксировать свои первые впечатления на бумаге.

Создавая продуманные и быстрые линии, постарайтесь не беспокоиться о том, как выглядит работа и не детализировать ее. Вы должны сосредоточиться на действии и ощущении.

Прим.ред. У Станислава Прокопенко aka Proko есть серия классных уроков по рисованию жестов на его Youtube канале. Стартовать можно отсюда:

А тут можно по таймеру открывать и прятать фотографии позирующих моделей для тренировки рисования жестов. Прямо из дома! Можно выбрать тип фото (портрет, пейзаж, части тела и т.д.), пол, количество одежды и время тренировки.

Совет 6. Используйте язык формы

Упрощение до простых геометрических форм отлично помогает передать характер персонажей

Использование различных форм — важный инструмент в дизайне персонажей. Они не только показывают индивидуальность героев, но также могут передавать движения или эмоции.
Персонаж, созданный с использованием квадрата, кажется медлительным и стабильным. Герой-треугольник передает более волнующие чувства. Круги или изогнутые линии часто используются для милых персонажей, они создают ощущение, что герой их дружелюбный и приятный по характеру.

Прим. ред. Вот тут можно почитать о том, как простые формы влияют на дизайн персонажей для мультиков.

Совет 7. Наклон и поворот

Если персонаж не стоит прямо, а сидит, наклонился или еще как-то согнулся, его поза мгновенно вызывает интерес

Хотите добавить позе динамики? Используйте наклоны и повороты. Все еще слишком статично? Поможет угол наклона: например, угол наклона плечей персонажа можно противопоставить углу его бедер. Вместо того, чтобы рисовать все параллельно, противопоставьте углы — это добавит ощущения плавности и ритма рисунку.

Совет 8. Применяйте сжатие и растяжение

Сжатие и растяжение — это фундаментальные принципы, которые должен знать каждый художник.
Это один из 12 принципов анимации. «Сжатие и растяжение» — полезная техника, она поможет придать рисунку жизни и энергии. В анимации сжатие часто используется перед более широким действием: растяжением.

То же самое можно делать в статичных рисунках: растянутая поза используется в момент, когда персонаж выполняет самое широкое действие, а сжатие в рисунке передаст напряжение.

Прим. ред. Все принципы анимации можно посмотреть тут:

Совет 9. Рисуйте тамбнейлы

Тамбнейлы рисуют так же быстро, как жесты

Тамбнейлы (их можно делать в форме рисунка жеста) пригодятся для планирования позы персонажа. Они помогут придумать различные варианты передачи одного и того же действия.

Когда я заканчиваю поиск в тамбнейлах, я дорабатываю скетч на новом слое. Такой подход помогает мне создавать более чистые рисунки, сохраняя изначальное ощущение движения.

Совет 10. Не забывайте о силуэтах

Запоминайте детали, чтобы понять, почему поза передана удачно (или не очень)

Попробуйте залить рисунок залит черным цветом, чтобы увидеть силуэт. Это отличный способ убедиться, что поза передана правильно. Если мыслить силуэтами, то легче понять, что самое важное в изображении позы.

Возможно, поза станет понятнее, если вы удлините конечности персонажа? Если заметили какую-то интересную особенность у персонажа, попробуйте подчеркнуть это в силуэте.

Совет 11. Добавьте ощущение массы

Масса влияет на то, как движется ваш персонаж

Ощущения веса в рисунке помогает создать более правдоподобное движение. Его можно передать через что угодно, начиная с одежды, которую носит персонаж, и заканчивая его позой.

Если персонаж держит нечто легкое, его поза не будет требовать усилий, а объект, возможно, не будет привлекать много внимания. Герой, который несет тяжелый предмет, будет всецело сосредоточен на том, чтобы удерживать его, что заставит его тело принимать необычное положение.

Совет 12. Рисуйте свободно

Эскизы, выполненные на скорую руку, станут полезным шаблоном для дальнейшей работы

Помимо жестов, рисуйте наброски на скорую руку, свободными штрихами. Это поможет сосредоточиться на отношении и истории, и не слишком привязываться к любой конкретной части изображения, которую вы рисуете.

Начиная с эскиза, выполненного свободными штрихами, вы сможете внести в него любые необходимые изменения. Например поменять позу или очертания силуэта, результатом чего станет более четкий дизайн. Затем, конечно, если вы довольны общей позой и жестом, скетч послужит цельным шаблоном, на который вы добавите необходимые детали.

Совет 13. Краткое описание пайплайна Бриттани

Я начинаю с быстрого поиска действия

Переходя от скетчинга к рисованию, я начинаю с быстрого эскиза, который передает основную идею. Обычно на этой стадии все выполняется довольно грубо, поэтому я могу сосредоточиться на позе, которую хочу изобразить, и не тратить слишком много времени на детали, над которыми буду работать позже.

Цвета, изогнутые линии и силуэты должны работать вместе

Затем я добавляю цвет. Это помогает мне выделить формы. На этом этапе работа с силуэтом может быть полезна, при этом следует учитывать и другие элементы дизайна, такие как прямые и изогнутые линии. Я вношу необходимые изменения, чтобы убедиться, что поза выглядит хорошо.

Добавляю финальные штрихи и устраняю ошибки

Наконец, на новом слое я начинаю добавлять детали. Я рисую и совершенствую скетч, чтобы придать ему больше структуры и формы, вношу окончательные изменения в персонажа и прорабатываю анатомию, которая, возможно, не была должным образом учтена на первоначальном скетче.

Совет 14. Развивайте свою идею. Гипертрофируйте важное

Преувеличивайте, чтобы извлечь максимум пользы из образа

Часто повторно проработать первоначальный рисунок может быть очень полезным. Когда вы думаете о том, что хотите нарисовать, не всегда есть четкое представление о том, как выглядит это действие.
Например, предположим, вы хотите нарисовать своего персонажа, сидящим на стуле. Предположим, он отдыхает, и в этом действии есть смысл. Но как заставить его показать историю лучше? Возможно, ему скучно, и поэтому он сидит расслабленно, положив голову на руки. Добавьте преувеличенных движений и мелких деталей, чтобы сделать работу более выразительной.

Совет 15. Пусть лицо и тело выражают общую идею

Комбинации языка тела и мимики помогают художникам показать, о чем думают персонажи
Нам следует учитывать и то, что чувствует персонаж. Визуальные подсказки, такие как выражение лица и язык тела помогут быстро передать эмоции персонажа. Герой, который чувствует себя уверенно, будет стоять расправив плечи и высоко подняв голову. Робкий персонаж может скрестить руки на груди и опустить голову.

Прим. ред. Например, тут Стефан Сильвер показывает, как придает сидящему на стуле человеку впечатление заскучавшего по самое не могу

Совет 16. Рассказывайте историю

Что вы можете сказать о характере этой девушки?

Дизайн персонажей — это нечто большее, чем просто рисовать красивые картинки. Герой может выглядеть совершенным с точки зрения техники, с идеальными пропорциями и анатомией, но ему будет не хватать выразительности.

Помогите зрителю узнать персонажа получше. То, как герой реагирует на различные ситуации, раскрывает различные аспекты его личности. Каков ваш персонаж? Как его характер повлияет на его поведение в различных обстоятельствах?

Источник

Общие сведения

Под движением тела понимают процесс его перемещения из одной точки пространства в другую. Произошедшее действие исследуют относительно другого объекта или выбранных начальных координат. При этом положение вовсе не обязательно может изменяться сразу ко всем окружающим его телам. Например, стоящий человек на Земле находится в состоянии покоя по отношению к планете, но движется относительно Солнца.

В физике принято любое изменение определять в системе пространственных координат. За оси принимают перпендикулярные линии x, y, z. Совокупность данных, используемых для изучения движения, называют системой отсчёта.

Существует несколько видов механического перемещения (во времени) физической точки:

При движении тело проходит определённый путь. Описать его можно виртуальной линией, при этом она может быть как прямой, так и кривой. Именно она и называется траекторией движения. По сути, эта линия соединяет последовательно все положения точки в пространстве — от начальной до конечной. Длина отрезка является пройденным путём и считается векторной величиной.

Изменение радиус-вектора r (значения, задающего положение точки в пространстве относительно другого тела) описывает кинематический закон: r = r (t). В трёхмерных декартовых координатах его можно записать так: r = xe + ye + ze = (x, y, z). Вектор, построенный из начальной точки движущегося тела в расположение её в данный момент времени, то есть приращение радиус-вектора за определённый промежуток t, как раз и называют перемещением.

Результирующее движение же равно векторной сумме последовательных изменений положения. При прямолинейном перемещении вектор пути совпадает с соответствующим участком траектории, а модуль перестановки равняется пройденному расстоянию.

Время, за которое тело пройдёт по установленной траектории пути, называют скоростью. Фактически это быстрота изменения координаты. Физики, исследуя передвижение, изучают не только положение материальной точки в начальный и конечный момент времени, но и закон, по которому происходит перемещение. Другими словами, они определяют зависимость радиус-вектора от времени.

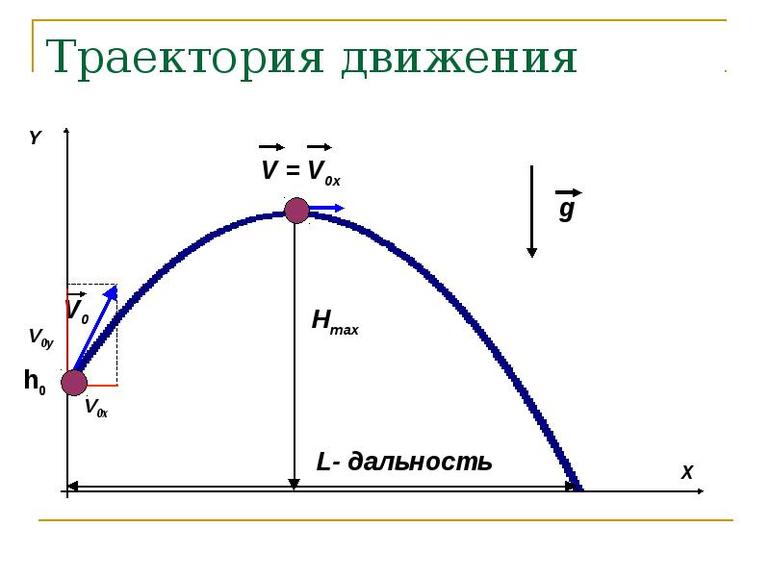
Горизонтальное перемещение

Пусть имеется тело, брошенное горизонтально поверхности. Высота падения равняется h, а начальная скорость V0. Здесь систему отсчёта удобно связать с Землёй. Объект будет передвигаться под действием силы тяжести. Остальными силами, например, сопротивлением воздуха, можно пренебречь. Тело перемещается в плоскости, содержащей вектора ускорения и свободного падения (g).

Скорость перемещения рассчитывают по формуле: V = √‎(V 2 x + V 2 y). После подстановки полученных ранее выражений равенство примет вид: V = √‎(V 2 0 + g 2 t 2 ). Отсюда следует, что уравнение для вектора движения материальной точки будет: s (t) = s0 + V0t + (g t 2 ) / 2, где: s0 — смещение тела, соответствующее начальному моменту времени.

Можно сделать вывод, что уравнение траектории не записывается через время, поэтому частица будет и перемещаться обратно по той же самой траектории. Временные отрезки между точками пути будут одинаковы как при прямом, так и при обратном движении.

Каждому положению соответствует определённое значение скорости, которое не зависит от направления перемещения. Нужно отметить, что наибольшей величиной в горизонтальной траектории полёта будет начальная точка.

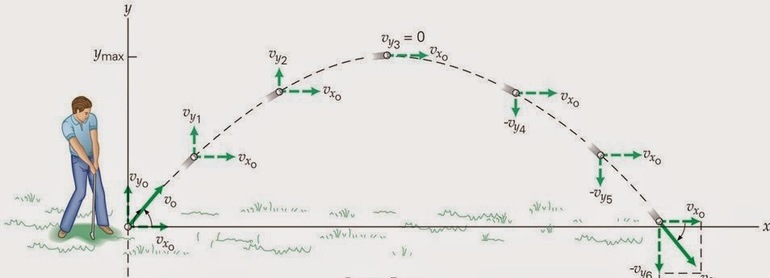
Движение тела под углом

Свободное падение является частным случаем равноускоренного, то есть на перемещаемый объект действует только сила притяжения. Если физическая точка перемещается, то кривая, которая описывается её радиус-вектором, обозначает пройденный путь. Эту траекторию можно описать некоторой математической функцией.

Итак, вектор скорости точки определяется как производная по времени: V = dr / dt = r. Ускорение же можно найти, продифференцировав скорость: a = dV / dt = d 2 r / dt. Если обозначить производную времени точкой, то формулу можно переписать так: a = V = r.

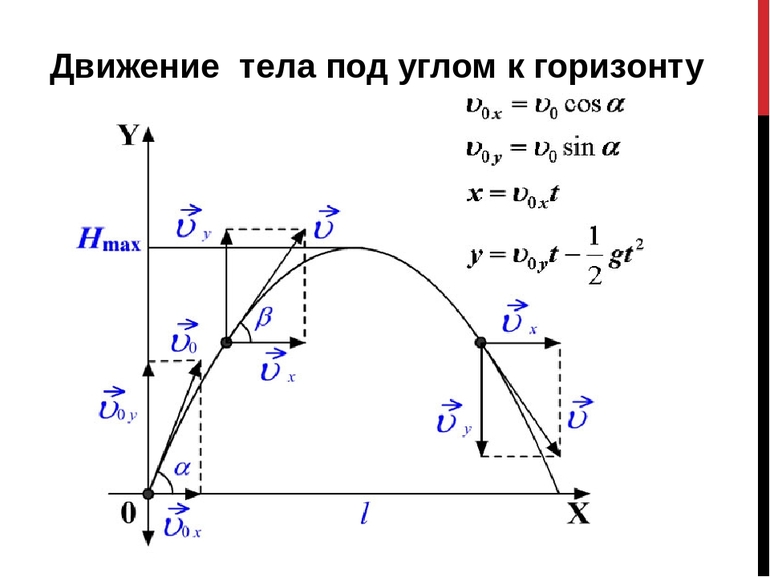
Для того чтобы вывести формулу, нужно воспользоваться основными выражениями, определяющими проекции:

Чтобы запись зависимости вертикальной оси от горизонтальной была как можно более компактной, соответствующие координаты rx и ry можно обозначить через икс и игрек. Из уравнения, связывающего координатную ось X и время, можно определить t как функцию ординаты. Линейное выражение будет иметь вид: t = x / (Vo * cosa).

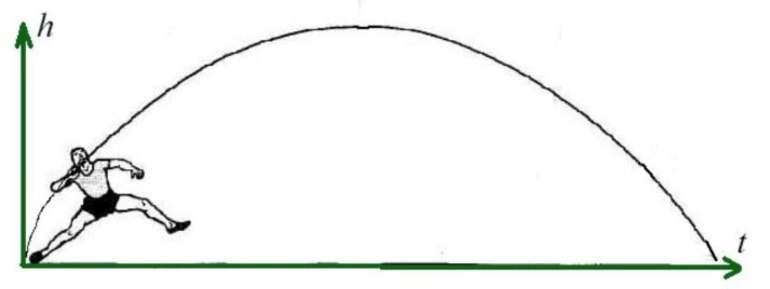
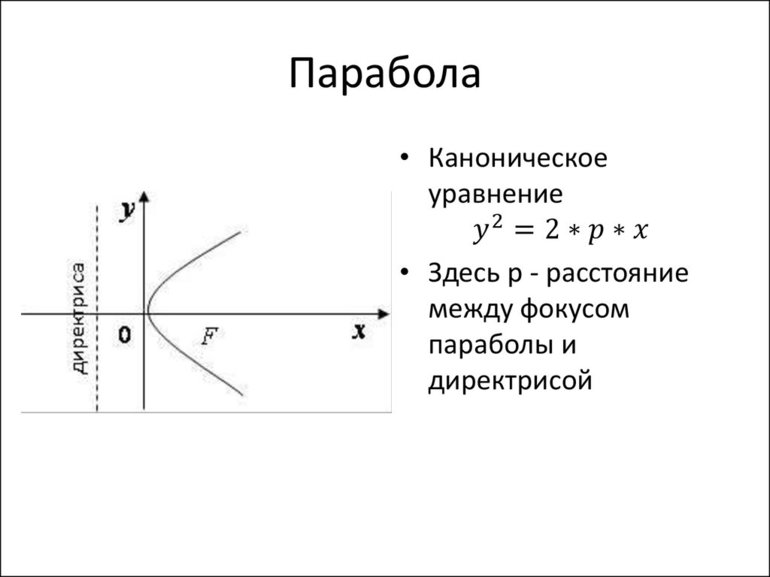
В итоге останется два слагаемых. Первое будет линейно по иксу, а второе квадратично. Таким образом, зависимость игрека от икса в уравнении траектории — это парабола (справа стоит квадратичная функция). Она проходит через начало координат. Если верно равенство x = 0, то игрек тоже будет равняться нулю.

Следует обратить внимание на то, что в квадрате стоит отрицательный коэффициент. Известно, что если перед квадратичным слагаемым в уравнении параболы стоит отрицательное число, то концы кривой будут направлены вниз.

Решение задач

Решение практических заданий лучше всего помогает закрепить полученные знания. Существуют физические сборники, которые интересны тем, что включают в себя различные примеры, приближенные к реалистичным задачам. Прорешивая их самостоятельно, ученик не только лучше разберётся в теме, но и научится применять полученные знания на практике.

Вот два таких задания:

Таким образом, чтобы успешно решать задачи, нужно знать несколько основных формул для определения местоположения тела, а также то, как выглядят уравнения параболы и прямой.

Стоит отметить, что существующие онлайн-калькуляторы не умеют вычислять формулы, описывающие траекторию пути. Но вместе с тем их можно использовать для выполнения расчётов или как справочники.

Источник