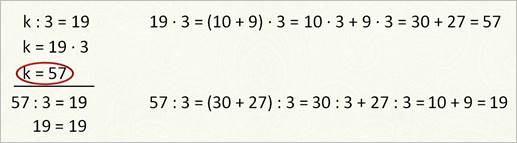Как решить уравнение видеоурок
Видеоурок по математике «Уравнение»
В математике принято и очень удобно обозначать неизвестное число буквой, затем составлять равенство и решать это равенство. Иначе говоря, составлять и решать уравнение. В этом уроке мы введём такие понятия, как «уравнение», «корень уравнения», «решение уравнения». Рассмотрим полезные правила для решения некоторых уравнений. А также научимся составлять и решать уравнения. Так что же называют уравнением? И что значит решить уравнение? В этом нам помогут разобраться два друга — Саша и Паша.
Саше по математике задали разгадать ребус, решение которого поможет узнать будущую тему урока. Но беда в том, что Саша совсем не умеет разгадывать ребусы. Его лучший друг Паша вызвался помочь.
Разгадав ребус, мальчишки понимают, что будущая тема урока — «Уравнение». И теперь Саше становится интересно узнать, что же должны уравнивать уравнения. На этот вопрос ребятам поможет найти ответ умный робот Электроша.
Умный робот Электроша с радостью расскажет, что называют уравнением. При этом он не забудет показать, как составляют и решают уравнения, да ещё и познакомит ребят с таким важным понятием, как «корень уравнения».
Чтобы мальчишки ещё лучше научились решать уравнения, Электроша познакомит их с полезными правилами решения некоторых уравнений.
А затем Электроша предложит ребятам выполнить несколько заданий на закрепление новых знаний.
Как решить уравнение видеоурок
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке Вы познакомитесь с такими понятиями, как уравнение и корень уравнения. Кроме того, узнаете, что значит решить уравнение и каким образом находить неизвестные переменные в нем.
Давайте рассмотрим задачу про грибы:
В корзине лежало несколько грибов. После того, как в нее положили еще 7 грибов, их стало 35. Сколько грибов было в корзине?
Обозначим неизвестное число грибов, лежащих в корзине латинской буквой х, после того как в нее добавили еще 7 грибов, стало х + 7 грибов в корзине, то есть 35. Значит должно выполняться равенство х + 7 = 35. Теперь надо найти такое значение х, при котором выполняется данное равенство. По смыслу вычитания, таким значением будет разность чисел 35 минус 7, то есть 28. Или же х = 28. Значит, в корзине было 28 грибов.
Если в равенство входит буква, или правильно говорить переменная, то равенство может быть верным при одних значениях этой буквы, т.е. переменной и неверным при других ее значениях. Например, х + 11 = 24. Это равенство будет верным при х = 13, и неверным при х = 1 или х = 2 и так далее. Так вот, уравнением называют равенство, содержащее букву, значение которой надо найти. Или же уравнение – это равенство, содержащее переменную, значение которой надо найти.
Значение буквы, или значение переменной при котором из уравнения получается верное числовое равенство, называют корнем уравнения.
Вернемся к последнему примеру.
Равенство х + 11 = 24 можно назвать уравнением, так как оно содержит переменную х, значение которой надо найти. Корнем данного уравнения является число 13, так при этом значении уравнение превращается в верное числовое равенство: 13 + 11 = 24.
Что же значит решить уравнение? Это значит, что надо найти все его корни или убедиться, что корней нет, то есть уравнение не имеет ни одного корня.
Например, решите уравнение: х + 22 = 56.
Решение: по смыслу вычитания, неизвестное слагаемое равно разности суммы и известного слагаемого, поэтому х = 56 – 22, то есть х = 34. Число 34 является корнем уравнения х + 22 = 56, так как 34 + 22 = 56. Обратите внимание, как находить корень в таких уравнениях: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Следующий пример, решите уравнение 21 – х = 19.
Решение: по смыслу вычитания, число 21 является суммой х и 19, то есть х + 19 = 21. Из этого уравнения находим неизвестное слагаемое х = 21 – 19, получим х = 2. Число 2 является корнем уравнения 21 – х = 19, так как равенство 21 – 2 = 19 является верным.
Обратите внимание, чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Рассуждая аналогичным образом, можно сформулировать еще одно правило, чтобы найти неизвестное уменьшаемое, надо к вычитаемому прибавить разность. Например, решите уравнение: у – 12 = 36. Для нахождения неизвестного уменьшаемого у, необходимо к разности 36 прибавить вычитаемое 12, получится 48. Ответ: корень уравнения у = 48. Действительно, если из 48 вычесть 12, получится 36.
Кстати, уравнение принято оформлять в столбик, найденное значение переменной подчеркивать горизонтальной линией, а ниже производить проверку уравнения, подставив полученный корень в исходное равенство.
При чтении уравнений и буквенных выражений помните, что названия латинских букв – переменных Х, Y, Z – мужского рода, а названия остальных латинских букв – среднего рода, например, «х=5», или «y=2» или же «а=7».
Названия букв в математике не склоняются. Например, данное выражение (х + 11 = 30) читается так: сумма х и одиннадцати равна тридцати.
Другой пример, данное уравнение (р – 15 = 47) можно прочитать как разность P и пятнадцати равна сорока семи.
Таким образом, на этом уроке Вы познакомились с такими понятиями, как уравнение и корень уравнения, а также узнали, что решить уравнение – это значит найти все его корни или убедиться, что корней нет. Кроме того, научились находить неизвестные переменные в уравнении.
Как решить уравнение видеоурок
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке познакомимся с понятиями «переменная» и «постоянная», научимся решать уравнения способом переноса слагаемых из одной части в другую.
Рассмотрим буквенное выражение 13 + 25х.
Значение данного выражения зависит от того, какое значение будет иметь х. Заметим, что значения х можно изменять, поэтому величины, обозначенные буквами в буквенных выражениях, называют переменными. В отличие от них значения величин, которые не меняются, называются постоянными. В нашем буквенном выражении постоянными величинами будут числа 13 и 25, а переменной является х.
Термины «переменные» и «постоянные» в математике отвечают на вопрос «что?» и являются именами существительными.
Перейдем к уравнениям.
Вспомним, уравнение – это равенство с неизвестным, значение которого надо найти. Неизвестное в уравнении обозначается буквой. Решая уравнение, находят значения, при подстановке которых вместо неизвестного получается верное числовое равенство. Эти значения неизвестного в уравнении называются корнями уравнения. Уравнение может иметь один корень, множество корней и вовсе не иметь такового.
Важно также отметить, что при нахождении корней приходится совершать с частями уравнения различные действия, которые не должны влиять на равенство между ними. Как это сделать? Представим уравнение в виде чашечных весов, находящихся в равновесии. Какой массы предмет положим на одну чашу весов, такой же массы предмет нужно положить на другую чашу, чтобы сохранить равновесие. Так и в уравнении, можно обе части уравнения умножить (или разделить) на одно и то же число, кроме 0, или к каждой части уравнения прибавить одно и то же число, на значение корня уравнения это не повлияет, так как «весы» при этом останутся в равновесии.
Выполним практические задания.
Найдем корень уравнения 6х = 30.
Посмотрим на левую часть уравнения, она представляет собой произведение числа (его называют коэффициентом) и переменной.
Правая часть уравнения – число.
Для того чтобы найти корень данного уравнения, разделим обе части уравнения на коэффициент при переменной
6х : 6 = 30 : 6; 6х :6 = х; 30 : 6 = 5; получим х =5.
Таким образом, можно сделать вывод, что для решения уравнений рассмотренного вида можно обе части уравнения разделить на коэффициент при переменной.
Решим уравнение такого же вида, в котором коэффициентом является обыкновенная дробь:
Чтобы в левой части уравнения избавиться от обыкновенной дроби, сохраняя при этом равенство верным, умножим каждую часть уравнения на одно и то же число, в данном случае на 5:
Сделаем вывод: для решения уравнения можно умножить или разделить обе части уравнения на одно и то же число, кроме 0. Ноль мы исключили, так как на 0 делить нельзя, а при умножении на 0 получается 0.
Рассмотрим решение еще одного уравнения:
Получим 16х – 2 + 2 +(– 6х) = 6х + 8 +2 + (-6х).
Тогда получится: 16х – 6х= 8+2.
Разделим каждую часть уравнения на коэффициент при переменной:
Обратите внимание, на третью строку записи решения уравнения 16х – 6х= 8+2 и сравните с первой. Фактически мы перенесли слагаемое 6х из правой части уравнения в левую, а слагаемое 2 из – левой части уравнения в правую, поменяв при этом в каждом случае знаки на противоположные.
Итак, чтобы решить уравнение нужно:
1. слагаемые, содержащие переменную, перенести в левую часть уравнения, слагаемые, не содержащие переменную, перенести в правую часть, поменяв при этом в каждом случае переноса знак слагаемого на противоположный;
2. привести подобные слагаемые в обеих частях уравнения;
3. разделить обе части уравнения на коэффициент при переменной.
Таким образом, в этом уроке Вы познакомились с такими понятиями как «переменная» и «постоянная», а так же научились решать уравнения, применяя способ переноса слагаемых из одной части в другую.
Решение уравнений
Урок 34. Математика 3 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Решение уравнений»
Сегодня я хочу вам напомнить о том, что такое уравнения, и как решать уравнения, в которых стоят знаки умножения и деления. А начну я с того, почему уравнение так называется.
Уравнение – это математическое равенство, в котором есть одно или даже несколько неизвестных. Эти неизвестные обычно обозначаются буквами латинского алфавита (а + 12 = 17, 78 – в = 24, с – 32 = 19, х × 4 = 56, 98 : у = 7, k : 3 = 19, 3z – 2r = 2).
Видите, во всех этих записях стоит знак равно.
Это значит, что при решении уравнений надо найти такое значение неизвестного, при котором левая часть уравнения будет равна правой.
Вы уже умеете решать уравнения, в которых стоят знаки плюс или минус. Помните, для решения таких уравнений мы пользуемся правилами:
* Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
* Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность.
* Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
А ещё решать уравнения нам помогали схемы.
На первой из них видно, что слагаемые являются частями. Поэтому их мы находим вычитанием. Ведь если нам, например, надо взять часть яблока или груши, мы её отрежем, то есть вычтем.
А вот сумма – это целое, получить которое можно сложением частей.
Вторая схема нам подсказывает, что целым является уменьшаемое. А так как это целое, то его мы будем находить действием сложения. А вот вычитаемое – часть, поэтому его мы найдём вычитанием.
А как же решать уравнения, если в них не действия сложения или вычитания, а умножение и деление? Вот, например, такое уравнение.
В нём надо найти такое значение икс, при умножении которого на четыре получится пятьдесят шесть. Ещё во втором классе мы с вами говорили о связи между компонентами и результатом действия умножения:
Если произведение двух множителей разделить на один из них, то получится другой множитель.
Значит, неизвестный множитель надо находить действием деления. Найдём его. Решение будем записывать под уравнением.
Пишем: икс равен частному чисел пятьдесят шесть и четыре. Так-так, надо посчитать. Все расчёты можно записывать справа от уравнения.
Пятьдесят шесть это сорок и шестнадцать. Делим каждое на четыре. Десять и четыре. Четырнадцать. Отступаю клеточку вниз и пишу: икс равен четырнадцати. Но, конечно, не забываю и про проверку. Черта, под которой пишу наше уравнение точно такое же, как оно было записано в верхней строчке, только вместо буквы подставляю её значение. Получился решённый пример. Но мы обязательно должны проверить, правильно ли он решён. Для этого выполним действие, которое находится слева от знака равно. Умножим четырнадцать на шесть.
Полученное число пишем внизу под левой частью уравнения. А число из правой части уравнения просто переносим. Видите, результат действия в левой части и правая часть между собой равны. Значит, уравнение решено верно. Корень уравнения равен четырнадцати.
А как же решать уравнения, в которых стоит знак деления?
И тут нам на помощь придут правила связи между компонентами и результатом действия деления.
Вот посмотрите на это уравнение.
В нём неизвестно делимое. Вспоминаем правило: Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Принимаемся за работу. К равно девятнадцать умножить на три. Получилось пятьдесят семь. Значит, k равно пятидесяти семи.
Подчёркиваю, и списываю наше уравнение, заменив букву k полученным значением. А теперь обязательно выполняю действие из левой части нашего уравнения. Пятьдесят семь разделить на три. Получилось девятнадцать. И справа тоже число девятнадцать. Есть равенство. Значит, уравнение решено верно и корень его равен пятидесяти семи.
А если в уравнении на деление надо найти неизвестный делитель, как вот в этом уравнении?
И вновь на помощь приходит правило: Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Решаем уравнение: 98 : у = 7.
Игрек равен частному чисел девяносто восемь и семь. Игрек равен четырнадцати. Проверяем. Записываем уравнение, заменив букву на число четырнадцать. Здесь придётся воспользоваться методом подбора, то есть умножить четырнадцать на такое однозначное число, чтобы в ответе получилось девяносто восемь. Но, так как справа записано число семь, попробую-ка я сразу умножить четырнадцать на семь. Отлично, произведение чисел четырнадцать и семь равно девяносто восьми. Все получилось. Корень уравнения равен четырнадцати.
Для решения этих уравнений мы воспользовались правилами связи между компонентами и результатом действий умножения и деления.
* Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
* Чтобы найти неизвестный делитель, надо делимое разделить на частное.
* Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Но вот некоторым ребятам бывает трудно запоминать все правила. А нельзя ли воспользоваться какой-нибудь короткой схемой, как мы это сделали при решении уравнений на сложение и вычитание? А почему бы и нет.
Для решения уравнений с действием умножения воспользуемся схемой, которой пользовались при решении уравнений, в которых стоит знак плюс. А для решения уравнений с действием деления воспользуемся схемой, которой пользовались при решении уравнений, в которых стоит знак минус. Просто заменим в схемах знаки.
Посмотрите, в первой схеме множители – это части, а произведение – целое. Части мы будем находить действием, обратным умножению – делением. А ведь наше правило об этом и говорит.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Вот, допустим, надо решить такое уравнение: три умножить на икс равно тридцать шесть.
Подставляем его в нашу схему.
Икс – это часть. Находим делением. Икс равен двенадцати. Проверяем. Умножаем три на двенадцать. Тридцать шесть. И справа тридцать шесть. Уравнение решено верно. Схема работает!
А теперь проверим вторую схему. Игрек разделить на семь равно одиннадцать
Подставили его в схему.
Найти надо делимое. Это целое. Находим умножением. И правило об этом говорит.
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
И здесь схема сработала. А справится ли наша схема с неизвестным делителем, попробуйте проверить сами. Решите вот это уравнение.
Ну вот и всё. Пришла пора нам с вами прощаться. Но я думаю, вы запомните правила, которые помогут вам решить любое уравнение.
* Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
* Чтобы найти неизвестное делимое, надо частное умножить на делитель.
* Чтобы найти неизвестный делитель, надо делимое разделить на частное.
А если вдруг забудете его, вы всегда сможете воспользоваться схемами.
А я сегодня прощаюсь с вами. До встречи, ребята!
Решение уравнений
Урок 43. Математика 2 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Решение уравнений»
— Добрый день, мои дорогие друзья! Сегодня мы с вами будем учиться решать уравнения.
А что же такое уравнение?
Помните, в первом классе вы решали примеры, в которых были пропущены числа?
Для того, чтобы вставить число в таких примерах, надо было вспомнить состав чисел в пределах 10.
А теперь вместо окошечек вы будете записывать буквы латинского алфавита:
Эти буквы сейчас используют в английском, немецком, французском и многих других языках. Вот посмотрите, как будут выглядеть наши примеры, в которых вместо окошек появились латинские буквы:
Давайте среди приведённых записей найдём уравнение:
Вторая запись. Конечно, и эта запись не будет являться уравнением, ведь это неравенство.
Следующая запись. Это равенство и оно содержит латинскую букву. Значит, эту запись мы назовём уравнением.
И ещё одна запись. Конечно это не уравнение, ведь эта запись не является равенством.
Итак, среди приведённых записей уравнением является третья запись. Давайте попробуем его решить.
А что значит «решить уравнение»?
Те уравнения с окошечками, которые были в первом классе, решать было легко. Выучил состав чисел в пределах 10, и подставляй нужное число. А вот если уравнение с двузначными числами, или с трёхзначными? Тут знание состава однозначных чисел нам не поможет.
Как же найти для решения нашего уравнения такое число, при котором получится верное равенство, т.е. найти корень уравнения?
Конечно, для того, чтобы найти верный способ решения уравнений, необходимо помнить правила:
· Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
· Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
· Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Сейчас попробуем решить наше уравнение 45 + x = 68.
В этом уравнении неизвестным является слагаемое. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Давайте выполним проверку, уточним, верно ли мы нашли неизвестное число.
Вновь записываем наше уравнение, но вместо буквы икс пишем число 23:
Слева и в справа получили одно и тоже число значит, уравнение решено верно.
Как я уже говорила, для того:
· Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
· Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
· Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
То есть, надо знать три правила. Но я вам предлагаю ещё один способ выбора действия при решении уравнений.
Представьте себе яблоко. Сейчас оно целое. А если мы его разрежем и отодвинем одну часть, у нас останется вторая часть. Отодвигая, мы выполняли действие вычитание. Значит, чтобы найти часть, надо выполнить действие вычитание. А теперь давайте вернём назад нашу часть. У нас опять получилось целое яблоко. Чтобы получить целое яблоко, мы сложили части. А теперь представим себе это схематически:
Теперь все наши уравнения мы будем соотносить с полученными схемами.
Вот, например, такое уравнение:
Давайте проверим. Записываем наше уравнение, только вместо буквы запишем полученное число, получаем:
В нашем уравнении было неизвестно слагаемое. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. Это мы и сделали.
Решим ещё одно уравнение:
Уравнение решено верно, то есть найден корень уравнения. Он равен 46.
В этом уравнении нам были известны вычитаемое и разность. Неизвестно уменьшаемое. Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое. Что мы и сделали.
Ну и давайте решим ещё одно уравнение:
В этом уравнении, как и в предыдущем также выполняется вычитание. Но здесь известно уменьшаемое и разность, а неизвестно вычитаемое. Опять подставляем уравнение к схеме. Нам надо найти вычитаемое, т.е. часть. А как его найти? Часть всегда находится вычитанием. Надо из целого, т.е. уменьшаемого вычесть часть, т.е. разность.
Получили верное равенство. Значит, уравнение решено верно, и число 50 является корнем уравнения. Нам надо было найти неизвестное вычитаемое, и мы из уменьшаемого вычитали разность.
Уравнения мы решили, а теперь давайте повторим то, что вы сегодня узнали на уроке.
При решении уравнений необходимо знать правила:
· Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
· Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
· Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Для того чтобы безошибочно решать уравнения запомните наши схемы. Они всегда подскажут вам, какой способ решения уравнений нужно выбрать. Если надо найти целое, мы выполняем действие сложение. А если часть, то вычитание. А теперь обратите внимание на алгоритм решения уравнений:
2) Применить правило нахождения неизвестного:
· Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
· Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
· Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Выполнить действие и получить корень уравнения.
3) Выполнить проверку.
Постарайтесь запомнить все эти правила и тогда вы без труда сможете решать уравнения, т.е. находить их корни.
А я прощаюсь с вами и желаю вам в этом успехов при решении уравнений.