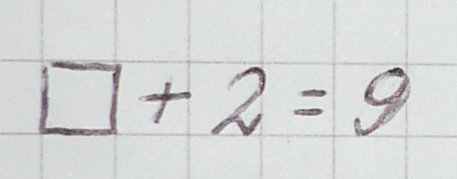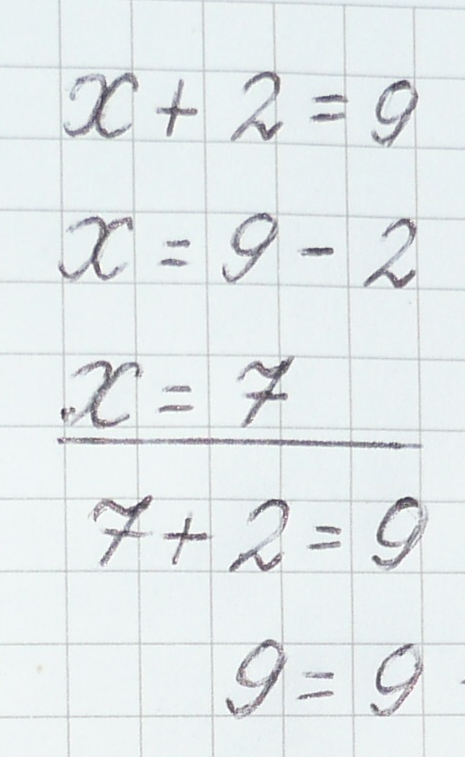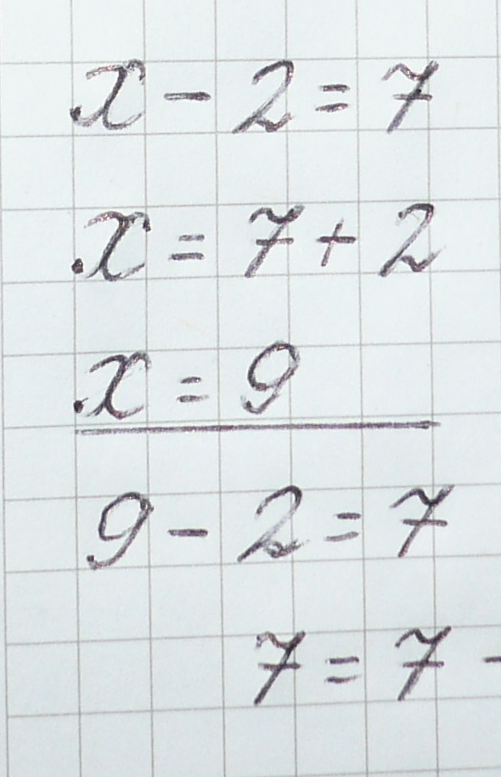Как решить уравнение объяснение

Что поможет в решении:

Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе.

А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1.

5х — 15 + 2 = 3х — 2 + 2х — 1

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Пример 4. Решить: 4(х + 2) = 6 — 7х.

Пример 5. Решить:

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

5х — 15 + 2 = 3х — 2 + 2х — 1

Пример 7. Решить: 2(х + 3) = 5 — 7х..

Источник

Решение простых уравнений. 5 класс

Уравнение — это равенство, содержащее букву, значение которой надо найти.

В уравнениях неизвестное обычно обозначается строчной латинской буквой. Чаще всего используют буквы « x » [икс] и « y » [игрек].

Решив уравнение, всегда после ответа записываем проверку.

Информация для родителей

Уважаемые родители, обращаем ваше внимание на то, что в начальной школе и в 5 классе дети НЕ знают тему «Отрицательные числа».

Поэтому они должны решать уравнения, используя только свойства сложения, вычитания, умножения и деления. Методы решения уравнений для 5 класса приведены ниже.

Не пытайтесь объяснить решение уравнений через перенос чисел и букв из одной части уравнения в другую с изменением знака.

Освежить знания по понятиям, связанным со сложением, вычитанием, умножением и делением вы можете в уроке «Законы арифметики».

Решение уравнений на сложение и вычитание

x + 9 = 15

x − 14 = 2

Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое.

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность.

6 + 9 = 15
15 = 15

16 − 2 = 14
14 = 14

Решение уравнений на умножение и деление

y · 4 = 12

y : 7 = 2

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

Чтобы найти неизвестное делимое, надо частное умножить на делитель.

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Источник

Начальные классы. Уравнения.

С уравнениями ученики знакомятся в 1 классе. Сначала решают примеры с окошком: выполняют действия с числами и задания на нахождение неизвестного числа, например было равенство:

И одно число решили спрятать:

Нам нужно догадаться, что за число спрятали?
Здесь прекрасно видно, чтобы найти неизвестное число, нужно из 9 — 2
Искомое число – 7.

В нашем равенстве – искомое число называют неизвестным числом.
А равенство, в котором одно число стало неизвестным, называется УРАВНЕНИЕМ.
Никто из вас никогда не видел, чтобы уравнения делали с «окошком». Это неудобно. Гораздо проще неизвестное обозначать буквами.

Неизвестное число обозначают маленькими латинскими буквами

или любой другой буквой.

И этому числу дают имя – корень уравнения.
Давайте посмотрим записи:
8+х
8+х>5
8+х =10
Только третья запись — уравнение. Потому что здесь есть неизвестное число и знак =.
Нам необходимо узнать это число.
Найти все значения х, при котором равенство будет верным — значит, решить уравнение, т.е. найти его корень.

При решении уравнения учитываем взаимосвязи между целым и частью:
— чтобы найти целое, надо сложить части;
— чтобы найти часть, надо из целого вычесть другую часть.

Если вы хотите более подробно узнать, как связаны целое и части, читайте тут.

Решение записывается так:

Корень пишем на следующей строке и подчеркиваем прямой линией.

Корень уравнения = 7, следовательно, наше уравнение решено.
Нам обязательно нужно проверить правильно мы нашли корень уравнения или нет.
Уравнение без проверки – это не уравнение.
Итак, в нашем уравнении корень –7, мы его подчеркнули, а теперь сделаем проверку. Для этого мы переписываем первую строку уравнения, но вместо неизвестного поставим значение корня.
Теперь: знак = пишем под знаком =. Число, записанное справа от знака равно: 9 – переписываем. Выражение, которое находится слева от знака равно: 7 + 2 – считаем. Получится 9. Это число 9 записываем слева от знака =.
Читаем выражение: 9 = 9. Значит, уравнение решили правильно.

Решим еще одно уравнение:

Ученикам начальной школы нужно обязательно овладеть математической речью. Для этого нужно знать, как называются компоненты при различных действиях, и как находится неизвестный компонент:

Если из суммы вычесть одно из слагаемых, то получится другое слагаемое.
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 65

Источник

Что такое уравнение и корни уравнения? Как решить уравнение?

Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.

Что такое уравнение? Смысл и понятия.

Узнаем сначала все понятия, связанные с уравнением.

Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.

Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.

Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.

Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.

Рассмотрим теперь, все термины на простом примере:
x+1=3

В данном случае x – переменная или неизвестное значение уравнения.

Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.

Получили верное равенство. Значит, правильно нашли корни уравнения.

Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.

Правила уменьшения или увеличения уравнения на определенное число.

Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7

Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.

Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.

Проверка:
Вместо переменной x подставим 5.

x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.

Разберем следующий пример:
Решите уравнение x-4=12.

Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:

Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16

Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.

Рассмотрим пример:
Решите уравнение 4+3x=2x-5

Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9

Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.

Правила уменьшения или увеличения уравнения в несколько раз.

Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.

Рассмотрим пример:
Решите уравнение 5x=20.

Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.

5x=20
5x :5 =20 :5
5:5x=4
1x=4 или x=4

Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅ 4 =20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.

Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.

Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.

7=7 получено верное равенство.

Ответ: корень уравнения равен x=21.

Следующий пример:
Найдите корни уравнения

Далее делим все уравнение на 3.

Сделаем проверку. Подставим в уравнение найденный корень.

Как решать уравнения? Алгоритм действий.

Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:

Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.

Источник

Алгебра. Урок 4. Уравнения, системы уравнений

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Уравнения”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Линейные уравнения

Примеры линейных уравнений:

Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение является линейным уравнением.

Примеры решения линейных уравнений:

Это линейное уравнение, так как переменная стоит в первое степени.

Попробуем преобразовать его к виду a x = b :

Для начала раскроем скобки:

− 2 x − 2 = 1 − 2 = − 1 2 = − 0,5

Это уравнение не является линейным уравнением, так как старшая степень, в которой стоит переменная x равна двум.

Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:

Это уравнение не является линейным уравнением.

Особые случаи (в 4 задании ОГЭ они не встречались, но знать их полезно)

Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:

Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:

Квадратные уравнения

Алгоритм решения квадратного уравнения:

Примеры решения квадратного уравнения:

D = b 2 − 4 a c = 6 2 − 4 ⋅ ( − 1 ) ⋅ 7 = 36 + 28 = 64

D > 0 – будет два различных корня:

x 1,2 = − b ± D 2 a = − 6 ± 64 2 ⋅ ( − 1 ) = − 6 ± 8 − 2 = [ − 6 + 8 − 2 = 2 − 2 = − 1 − 6 − 8 − 2 = − 14 − 2 = 7

Ответ: x 1 = − 1, x 2 = 7

D = b 2 − 4 a c = 4 2 − 4 ⋅ ( − 1 ) ⋅ ( − 4 ) = 16 − 16 = 0

D = 0 – будет один корень:

x = − b 2 a = − 4 2 ⋅ ( − 1 ) = − 4 − 2 = 2

D = b 2 − 4 a c = ( − 7 ) 2 − 4 ⋅ 2 ⋅ 10 = 49 − 80 = − 31

Также существуют неполные квадратные уравнения (это квадратные уравнения, у которых либо b = 0, либо с = 0, либо b = с = 0 ). Смотрите видео, как решать такие квадратные уравнения!

Разложение квадратного трехчлена на множители

Квадратный трехчлен можно разложить на множители следующим образом:

a x 2 + b x + c = a ⋅ ( x − x 1 ) ⋅ ( x − x 2 )

где a – число, коэффициент перед старшим коэффициентом,

x – переменная (то есть буква),

a x 2 + b x + c = a ⋅ ( x − x 0 ) 2

Примеры разложения квадратного трехчлена на множители:

− x 2 + 6 x + 7 = ( − 1 ) ⋅ ( x − ( − 1 ) ) ( x − 7 ) = − ( x + 1 ) ( x − 7 ) = ( x + 1 ) ( 7 − x )

− x 2 + 4 x − 4 = ( − 1 ) ⋅ ( x − 2 ) 2 = − ( x − 2 ) 2

Если квадратный трехчлен является неполным, ( ( b = 0 или c = 0 ) то его можно разложить на множители следующими способами:

Дробно рациональные уравнения

Для того, чтобы решить дробно рациональное уравнение, надо вспомнить, что такое ОДЗ и когда оно возникает.

ОДЗ – область допустимых значений переменной.

В выражении вида f ( x ) g ( x ) = 0

ОДЗ: g ( x ) ≠ 0 (знаменатель дроби не может быть равен нулю).

Алгоритм решения дробно рационального уравнения:

Пример решения дробного рационального уравнения:

Решить дробно рациональное уравнение x 2 − 4 2 − x = 1.

Решение:

Будем действовать в соответствии с алгоритмом.

Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:

x 2 − 4 2 − x − 1 \ 2 − x = 0

x 2 − 4 2 − x − 2 − x 2 − x = 0

x 2 − 4 − ( 2 − x ) 2 − x = 0

x 2 − 4 − 2 + x 2 − x = 0

Первый шаг алгоритма выполнен успешно.

Обводим в рамочку ОДЗ, не забываем про него: x ≠ 2

x 2 + x − 6 = 0 – Квадратное уравнение. Решаем через дискриминант.

D = b 2 − 4 a c = 1 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 1 + 24 = 25

D > 0 – будет два различных корня.

x 1,2 = − b ± D 2 a = − 1 ± 25 2 ⋅ 1 = − 1 ± 5 2 = [ − 1 + 5 2 = 4 2 = 2 − 1 − 5 2 = − 6 2 = − 3

Корни, полученные на предыдущем шаге:

Значит, в ответ идет только один корень, x = − 3.

Системы уравнений

Пример системы уравнений

Существует два метода решений систем линейных уравнений:

Алгоритм решения системы уравнений методом подстановки:

Решить систему уравнений методом подстановки

Решение:

y = − 28 − 7 = 28 7 = 4

x = 8 − 2 y = 8 − 2 ⋅ 4 = 8 − 8 = 0

Ответ можно записать одним из трех способов:

Решение системы уравнений методом сложения.

Метод сложения основывается на следующем свойстве:

Идея метода сложения состоит в том, чтобы избавиться от одной из переменных, сложив уравнения.

Решить систему уравнений методом сложения

Теперь, когда перед переменной в обоих уравнениях стоят противоположные коэффициенты, при сложении левых частей уравнений переменная x исчезнет.

( − 3 x − 6 y ) + ( 3 x − y ) = ( − 24 ) + ( − 4 )

− 3 x − 6 y + 3 x − y = − 24 − 4

y = − 28 − 7 = 28 7 = 4

Ответ можно записать одним из трех способов:

Задание №9 из ОГЭ 2020. Типовые задачи и принцип их решения.

Источник

• ← витамины для работоспособности мозга и памяти взрослым
• укажите цели правового регулирования отношений в сфере образования →