Как решить такой пример
Как решить любую задачу? Часть 1. Алгебра
Придумывать новое решение самостоятельно – это тоже навык, который надо развивать. Нужно привыкнуть не бояться нового, уметь задавать себе правильные вопросы и лояльно относиться к своим ошибкам. В этой статье я написала, что помогает лично мне и моим ученикам решать новые задачи.
Предупреждаю: это всё работает только если вы знаете необходимую теорию. То есть уметь отличать рубанок от ножовки всё-таки надо. 🙂
5 принципов которые помогут решить задачу:
Если закрыта одна дверь, открыта другая. Не циклись на одной мысли. Возможно, к решению можно подойти вообще с другой стороны. Но перед тем как зачеркивать очередную попытку решения – внимательно проверь, может быть ты просто сделал в нем какую-то простенькую ошибку и поэтому не получается дорешать до конца?
8 вопросов, которые помогут решить почти любое задание в алгебре
Решая задачу, мы ищем ответ на вопрос задания – нужное значение переменной, интервал решений или еще что-то в этом роде. И чтобы прийти к ответу на этот главный вопрос нужно уметь задавать себе промежуточные, опорные вопросы, которые могут натолкнуть на правильный путь рассуждений. Вот эти вопросы:
1. Что передо мной (уравнение, неравенство, выражение)? Как обычно решается такой тип задач?
— Что передо мной?
— Квадратное неравенство.
— Как решаются квадратные неравенства?
— Методом интервалов.

\(x∈[-10;10]\)
Пример 2: Решите уравнение \(\cos\) \(\frac<π(x-7)><3>\) \(=\) \(\frac<1><2>\)
— Что передо мной?
— Простейшее тригонометрическое уравнение.

\(\frac<π(x-7)><3>\) \(=±\) \(\frac<π><3>\) \(+2πn,n∈Z\)
— А теперь что передо мной?
— Хм… Выглядит странно, но похоже на линейное уравнение, так как тут только одна переменная (\(x\)) и она в первой степени.
— Как решаются линейные уравнения?
— Нужно избавиться от знаменателей, раскрыть все скобки и перенести известные вправо, а неизвестные влево, в общем, привести уравнение к виду \(x=[число]\).
2. Решал ли я похожие задачи? Как я их решал?
— Что передо мной?
— Тригонометрическое уравнение (не простейшее).
— Как обычно решаются тригонометрические уравнения?
— Уравнение преобразовывается с помощью формул, пока невозможно будет сделать замену. Очевидно, что тут сразу можно сделать замену.
Получилось кубическое уравнение.
— Решал ли я похожие задачи? Как я их решал?
— Обычно кубические уравнения я решал либо методом группировки, либо делением многочлена на многочлен.
3. Какие формулы я вижу / какие формулы можно применить? Что надо сделать, чтоб их можно было применить?
— Какие формулы я тут вижу?
— Полностью – никаких. Но вот такое же произведение синус на косинус есть в формуле двойного угла синуса:
4. Какие «неслучайности» я вижу? Как их можно использовать?
— Какие «неслучайности» я вижу?
— Очевидно, что выражения \((4x-8)\) и \((x-8)\) с той и другой стороны – это неспроста.
— Как их можно использовать?
— Поделить на эти выражения нельзя. Можно попробовать перенести то, что стоит справа в левую часть.
Теперь можно одинаковые выражения вынести за скобку.
— Какие «не случайности» можно заметить?
— И \(9\), и \(27\) являются степенями тройки: \(3^2=9\), \(3^3=27\).
— Как это можно использовать?
— Можно заменить \(9\) на \(3^2\), а \(27\) на\( 3^3\), вот так:
А теперь можно применить свойство степеней: \((a^n)^m=a^
5. Что я в принципе могу сделать? Какие преобразования допустимы/возможны?
— Что можно сделать с этим выражением?
— Можно вынести множители из-под знака корня.
— Какие еще преобразования здесь возможны?
— Можно вынести за скобки \(4\sqrt<2>\).
— Что еще можно сделать?
— Применить формулу двойного угла \(\cos2α=1-2\sin^2α \)
6. Что мне мешает? Как можно сделать выражение/уравнение/неравенство проще? Как мне было бы удобнее? Что я могу сделать, чтоб стало удобнее?
— Как можно сделать уравнение сильно проще?
— Если избавиться от корня, то уравнение станет проще.
— Как можно избавиться от корня?
— Можно возвести обе части уравнения в квадрат.
— Как можно упростить уравнение?
— Можно избавиться от знаменателя.
— Как обычно избавляются от знаменателя?
— Умножением обеих частей уравнения на наименьший общий знаменатель.
— Как было бы удобнее?
— Было бы удобнее, чтоб аргументы у логарифмов были одинаковые.
— Что надо сделать, чтоб аргументы у логарифмов были одинаковые?
— Вынести квадрат вперед и каким-то образом перевернуть дробь.
— Как можно перевернуть дробь?
— Можно использовать степень \(-1\).
— Что можно сделать теперь?
— Логарифмы полностью одинаковые значит можно либо сделать замену, либо вынести их за скобку.
7. Чего от меня хочет задача? Когда будет выполняться условие задачи?
Допустим, вы никогда не сталкивались с дробными неравенствами или забыли, как их решать. Давай просто порассуждаем.
— Чего от меня хочет задача?
— Чтоб левая часть была положительна.
— А когда будет положителен числитель?
— Когда икс больше трех. Если же икс меньше трех, то числитель будет иметь знак минус.
— Тот же вопрос про знаменатель?
— Знаменатель положителен при иксе большем \(1\), и отрицателен при иксе меньше \(1\).
— Так когда же будет выполняться условие задачи?
— При иксе большем \(3\) (там в дроби и сверху и снизу плюс) и при иксе меньше \(1\) (в этом случае и числитель, и знаменатель имеют знак минус).
— Чего от меня хочет задача?
— Чтоб я нашел такие иксы, при которых слева – ноль.
— А что у нас стоит слева?
— Сумма двух квадратов.
— В каком случае сумма квадратов будет равняться нулю?
— Хм… Квадрат не может быть отрицательным, он всегда больше либо равен нуля. А мы складываем два таких выражения. Значит, нам нужны такие иксы, при которых оба квадрата ОДНОВРЕМЕННО обратятся в ноль, потому что в остальных случаях сумма будет больше нуля.
8. Могу ли я сделать какую-нибудь замену?
— (вспоминаем предыдущие пункты) Какие неслучайности я вижу?
— В скобке вторая дробь – это перевернутая первая.
— Как это можно использовать?
— Ну…
— Какие преобразования тут возможны в принципе?
— О! Можно перенести всё влево и разложить на множители по формуле разности квадратов!
— Что можно теперь сделать?
— Можно привести выражения в скобках к общему знаменателю.
Итого: приучайтесь рассуждать в математике. Не мыслите шаблонами, а ищите путь. И написанные выше вопросы вам в этом помогут. Успешных решений!
Решение задач онлайн
Сервисы, которые помогают всем решать задачи.
Онлайн-калькуляторы постоянно совершенствуются.
Кусочно-заданная функция
Укажите кусочно-заданную функцию и перейдите к нужному вам сервису, например, к одному из: нахождению интеграла, производной, исследованию и построение графика и др.
Решение уравнений
Это сервис позволяет решать уравнения, в том числе получить подробное решение, а также увидеть решение уравнения на графике.
Решение пределов
Этот сервис позволяет найти предел функции. Также рассматривается подробное решение правилом Лопиталя.
Производная функции
Это сервис, где можно вычислить производную функции, частную производную функции, а также производную неявно заданной функции.
Разложение в ряд
Здесь можно выполнить разложение в ряд Тейлора, Фурье, найти сумму ряда.
Системы уравнений
Позволяет решать системы линейных уравнений методом Крамера, методом Гаусса, а также вообще любые системы уравнений.
Решение неравенств
Решает неравенство, а также изображает решённое неравенство на графике.
Решение интегралов
Это сервис, где можно вычислить определённые, неопредёленные интегралы, а также двойные, несобственные, кратные.
График функции
Это сервис построения графиков на плоскости и в пространстве. Приводится подробное решение на исследование функции.
Решение систем неравенств
Вы можете попробовать решить любую систему неравенств с помощью данного калькулятора систем неравенств.
Комплексные числа
Здесь можно вычислить комплексные выражения: находить формы (алгебраическую, тригонометрическую, показательную); модуль и аргумент, сопряжённое, геометрическую интерпретацию.
Решение матриц
Таблицы
Использование калькуляторов
В статьях ниже приведены примеры, как использовать калькуляторы в соотв. темах:
Интересные калькуляторы
Здесь приведены новые сервисы, которые помогут вам при решении некоторых задач:
Как пользоваться Контрольная Работа РУ
Здесь приведены последние статьи про использование калькуляторов.
Решение векторов
Теперь Вы можете не тратить свое время на такие простые задачи, как нахождение длины вектора, скалярного произведение векторов, расстояние между двумя точками на плоскости и в пространстве.
Физика онлайн
Физика онлайн позволяет посмотреть физические эксперименты он-лайн!
Теория вероятности
Теория вероятности онлайн позволяет вычислять без проблем математическое ожидание, дисперсию, число перестановок, сочетаний, размещений и факториал.
Другое
Здесь представлены различные онлайн калькуляторы, и в том числе:
обычный инженерный математический калькулятор калькулятор онлайн.
Порядок действий в математике
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные операции в математике
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Подставляем полученные значения в исходное выражение:
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!
Решение простых линейных уравнений
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.
В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении: Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа. Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством. Числовой коэффициент — число, которое стоит при неизвестной переменной. Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз: Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем. Как решать простые уравненияЧтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила. 1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный. Для примера рассмотрим простейшее уравнение: x+3=5 Начнем с того, что в каждом уравнении есть левая и правая часть. Перенесем 3 из левой части в правую и меняем знак на противоположный. Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2. Решим еще один пример: 6x = 5x + 10. Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус. Приведем подобные и завершим решение. 2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок. Применим правило при решении примера: 4x=8. При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение. Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица. Разделим каждую часть на 4. Как это выглядит: Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения: Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12 Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах. Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные. Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки. Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе. А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе. Примеры линейных уравненийТеперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе! Пример 1. Как правильно решить уравнение: 6х + 1 = 19. Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1. 5х — 15 + 2 = 3х — 2 + 2х — 1 Ответ: х — любое число. Пример 3. Решить: 4х = 1/8. Пример 4. Решить: 4(х + 2) = 6 — 7х. Пример 5. Решить: Пример 6. Как решить линейное уравнение: х + 7 = х + 4. 5х — 15 + 2 = 3х — 2 + 2х — 1 Пример 7. Решить: 2(х + 3) = 5 — 7х.. Порядок выполнения действий, правила, примерыКогда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения. В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций. Порядок вычисления простых выраженийВ случае выражений без скобок порядок действий определяется однозначно: Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций. Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты. Решение В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения: Решение Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо. Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три. Решение 17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2 Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ: 17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7 Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем. Что такое действия первой и второй ступениИногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение. К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление. Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так: В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении). Порядок вычислений в выражениях со скобкамиСкобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так: Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо. Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером. Решение Теперь нам нужно подставить получившиеся значения в первоначальное выражение: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2 Начнем с умножения и деления, потом выполним вычитание и получим: 5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6 На этом вычисления можно закончить. Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу. Решение Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним. Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциямиЕсли у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки. Разберем пример такого вычисления. Решение Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание. ( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13 В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
|
|---|








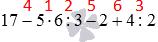 .
.