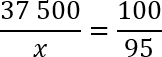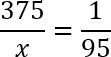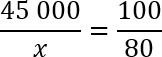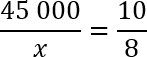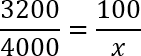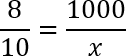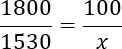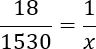Как решить пропорцию с процентами
Метод решения задач с процентами
Все соотношения и формулы, полученные для решения задач с процентами выводятся из пропорции
Данные задачи на проценты можно записать в виде следующих соотношений:
которые можно записать в виде пропорции
| все | = | 100% |
| часть | часть в % |
Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.
Примеры решения задач на проценты
30 соответствует 100% x соответствует 15%
решим полученное уравнение
| x = | 30 · 15% | = 4.5 |
| 100% |
Ответ: 15% от 30 равно 4.5.
20 соответствует 100% 35 соответствует x
решим полученное уравнение
| x = | 35 · 100% | = 175% |
| 20 |
Ответ: 35 составляет 175% от 20.
x соответствует 100% 20 соответствует 5%
решим полученное уравнение
| x = | 20 · 100% | = 400 |
| 5% |
Ответ: 400.
При изучении процентов вам также будут полезны:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Как решать задачи с процентами
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.
Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».
Процент — это одна сотая часть от любого числа. Обозначается вот так: %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить число на 100, как в примере выше.
А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:
А вот, как перевести проценты в десятичную дробь — обратным действием:
Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а потом используем предыдущее правило:
Типы задач на проценты
В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.
Тип 1. Нахождение процента от числа
Чтобы найти процент от числа, нужно число умножить на процент.
Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?
Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).
Из общего количества изготовленных стульев контроль не прошли 100 штук.
Тип 2. Нахождение числа по его проценту
Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.
Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.
Задача. Школьник решил 38 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?
Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 38 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.
38/0,16 = 38 * 100/16 = 237,5
Значит 237 задачи включили в этот сборник.
Тип 3. Нахождение процентного отношения двух чисел
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.
Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?
Как решаем: возьмем алгоритм из правила выше:
10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%
В классе учится 10 девочек — это 40%.
Тип 4. Увеличение числа на процент
Чтобы увеличить число на некоторое количество процентов, нужно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.
Формула расчета процента от числа выглядит так:
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом месяце стикер-пак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикер-пак?
Как решаем: подставим в формулу данные из условий задачи.
110 * (1 + 12/100) = 110 * 1,12 = 123,2.
Стоимость стикер-пака в этом месяце — 123 рубля 20 копеек.
Тип 5. Уменьшение числа на процент
Чтобы уменьшить число на несколько процентов, нужно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.
Формула расчета выглядит так:
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом году школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?
Как решаем: подставим в формулу данные из условий задачи.
75 выпускников закончат школу в этом году.
Тип 6. Задачи на простые проценты
Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.
Формула расчета выглядит так:
где a — исходная сумма,
S — сумма, которая наращивается,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Родители взяли в банке кредит 5000 рублей, чтобы купить тебе что-то классное. Кредит на год под 15% ежемесячно. Сколько денег они внесут через год?
Как решаем: подставим в формулу данные из условий задачи.
5000 * (1 + 12 * 15/100) = 14000
Родители через год внесут в банк 14000 рублей.
Тип 7. Задачи на сложные проценты
Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.
Формула расчета выглядит так:
где S — наращиваемая сумма,
a — исходная,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Папа взял в банке кредит 25000 рублей на 3 месяца под 15%. Нам нужно узнать, сколько денег придется заплатить банку по истечении срока кредита.
Как решаем: просто подставим в формулу данные из условий задачи:
25000 * (1 + 15/100)3 = 38021,875 — искомая сумма.
Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!
Способы нахождения процента
Универсальная формула для решения задач на проценты:
| A * b = C, где A — исходное число, b — проценты, переведенные в десятичную дробь, C — новое число. |
Чтобы применить алгоритм, нужно прочитать задачу, отметить, какие два числа нам известны и найти третье.
Есть еще четыре способа поиска процентов. Рассмотрим каждый из них.
Деление числа на 100
При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.
Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?
Ответ: выгоднее воспользоваться скидкой 15%.
Составление пропорции
Пропорция — определенное соотношение частей между собой.
С помощью метода пропорции можно рассчитать любые %. Выглядит это так:
Читается: a относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.
Рассмотрим пример. На сколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?
Ответ: купить спортивную футболку выгоднее на 194,6 рубля.
Соотношения чисел
Есть случаи, при которых можно использовать простые дроби.
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Задачи на проценты с решением
Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.
Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?
76 : 100 = 0,76 — 1% от массы человека
Ответ: масса воды 53,2 кг
Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?
Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.
Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:
После двух понижений изменение цены составит:
Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.
Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?
По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто
Получается, что стоимость одной пары брюк — это 23% стоимости пальто.
Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.
Ответ: пять пар брюк на 15% дороже, чем одно пальто.
Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.
По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.
Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.
Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.
А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.
Ответ: заработок жены составляет 27%.
Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?
Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.
Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.
На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах.
Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.
Задачи на проценты: стандартный расчет с помощью пропорций
Сегодня мы продолжаем серию видеоуроков, посвященных задачам на проценты из ЕГЭ по математике. В частности, разберем две вполне реальных задачи из ЕГЭ и еще раз убедимся, насколько важно внимательно читать условие задачи и правильно его интерпретировать.
Итак, первая задача:
Задача. Только 95% и 37 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу B1?
На первый взгляд кажется, что это какая-то задача для кэпов. Наподобие:
Задача. На дереве сидело 7 птичек. 3 из них улетело. Сколько птичек улетело?
Тем не менее, давай все-таки сосчитаем. Решать будем методом пропорций. Итак, у нас есть 37 500 учеников — это 100%. А также есть некое число x учеников, которое составляет 95% тех самых счастливчиков, которые правильно решили задачу B1. Записываем это:
Перед нами классическая пропорция, но прежде чем воспользоваться основным свойством и перемножить ее крест-накрест, предлагаю разделить обе части уравнения на 100. Другими словами, зачеркнем в числителе каждой дроби по два нуля. Перепишем полученное уравнение:
По основному свойству пропорции, произведение крайних членов равно произведению средних членов. Другими словами:
Это довольно большие числа, поэтому придется умножать их столбиком. Напоминаю, что пользоваться калькулятором на ЕГЭ по математике категорически запрещено. Получим:
Итого ответ: 35 625. Именно столько человек из исходных 37 500 решили задачу B1 правильно. Как видите, эти числа довольно близки, что вполне логично, потому что 95% тоже очень близки к 100%. В общем, первая задача решена. Переходим к второй.
Задача на проценты №2
Задача. Только 80% из 45 000 выпускников города правильно решили задачу B9. Сколько человек решили задачу B9 неправильно?
Решаем по той же самой схеме. Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:
Давайте сократим по одному нулю в числителе и знаменателе 2-й дроби. Еще раз перепишем полученную конструкцию:
Основное свойство пропорции: произведение крайних членов равно произведению средних. Получаем:
Это простейшее линейное уравнение. Выразим из него переменную x :
Сокращаем по одному нулю у 45 000 и у 10, в знаменателе остается единица, поэтому все, что нам нужно — это найти значение выражения:
Можно, конечно, поступить так же, как в прошлый раз, и перемножить эти числа столбиком. Но давайте не будем сами себе усложнять жизнь, и вместо умножения столбиком разложим восьмерку на множители:
x = 4500 · 2 · 2 · 2 = 9000 · 2 · 2 = 36 000
А теперь — самое главное, о чем я говорил в самом начале урока. Нужно внимательно читать условие задачи!
Что от нас требуется узнать? Сколько человек решили задачу B9 неправильно. А мы только что нашли тех людей, которые решили правильно. Таких оказалось 80% от исходного числа, т.е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:
45 000 − 36 000 = 9000
Полученное число 9000 — это и есть ответ к задаче. Итого в этом городе из 45 000 выпускников 9000 человек решили задачу B9 неправильно. Все, задача решена.
Я надеюсь, что этот ролик поможет тем, кто самостоятельно готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Задачи на проценты: считаем проценты с помощью пропорции
В прошлом видеоуроке мы рассматривали решение задач на проценты с помощью пропорций. Тогда по условию задачи нам требовалось найти значение той или иной величины.
В этот раз исходное и конечное значения нам уже даны. Поэтому в задачах будет требоваться найти проценты. Точнее, на сколько процентов изменилась та или иная величина. Давайте попробуем.
Задача. Кроссовки стоили 3200 рублей. После повышения цены они стали стоить 4000 рублей. На сколько процентов была повышена цена на кроссовки?
Итак, решаем через пропорцию. Первый шаг — исходная цена была равна 3200 рублей. Следовательно, 3200 рублей — это 100%.
Что ж, условие задачи записано. Составляем пропорцию:
Дробь слева прекрасно сокращается на 100: 3200 : 100 = 32; 4000 : 100 = 40. Кроме того, можно сократить на 4: 32 : 4 = 8; 40 : 4 = 10. Получим следующую пропорцию:
Воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних. Получаем:
8 · x = 100 · 10;
8 x = 1000.
Это обычное линейное уравнение. Отсюда находим x :
Итак, мы получили итоговый процент x = 125. Но является ли число 125 решением задачи? Нет, ни в коем случае! Потому что в задачи требуется узнать, на сколько процентов была повышена цена на кроссовки.
На сколько процентов — это значит, что нам нужно найти изменение:
Получили 25% — именно настолько была повышена исходная цена. Это и является ответом: 25.
Задача B2 на проценты №2
Переходим ко второй задаче.
Задача. Рубашка стоила 1800 рублей. После снижения цены она стала стоить 1530 рублей. На сколько процентов была снижена цена на рубашку?
На основе полученной записи составляем пропорцию:
Давайте для упрощения дальнейших вычислений разделим обе части данного уравнения на 100. Другими словами, у числителя левой и правой дроби мы зачеркнем два нуля. Получим:
Теперь снова воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних.
18 · x = 1530 · 1;
18 x = 1530.
x = 1530 : 18 = (765 · 2) : (9 · 2) = 765 : 9 = (720 + 45) : 9 = 720 : 9 + 45 : 9 = 80 + 5 = 85
Как видите, мы не стали считать полученное частное уголком, а просто несколько раз сократили нашу дробь. При этом нам потребовалось разложить на множители числитель и
Мы получили, что x = 85. Но, как и в прошлой задаче, это число само по себе не является ответом. Давайте вернемся к нашему условию. Теперь мы знаем, что новая цена, полученная после снижения, составляет 85% от старой. И для того, чтобы найти изменения, нужно из старой цены, т.е. 100%, вычесть новую цену, т.е. 85%. Получим:
Это число и будет ответом: Обратите внимание: именно 15, а ни в коем случае не 85. Вот и все! Задача решена.
Внимательные ученики наверняка спросят: почему в первой задаче мы при нахождении разности вычитали из конечного числа начальное, а во второй задаче поступили в точности до наоборот: из исходных 100% вычли конечные 85%?
Давайте проясним этот момент. Формально, в математике изменением величины всегда называется разность между конечным значением и начальным. Другими словами, во второй задаче у нас должно было получиться не 15, а −15.
Однако этот минус ни в коем случае не должен попасть в ответ, потому что он уже учтен в условии исходной задачи. Там прямо сказано о снижении цены. А снижение цены на 15% — это то же самое, что повышение цены на −15%. Именно поэтому в решении и ответе задачи достаточно написать просто 15 — без всяких минусов.
Все, надеюсь, с этим моментом мы разобрались. На этом наш сегодняшний урок закончен. До новых встреч!
Решение задач на проценты
Методички Педсовета
Введение
Слово процент от латинского слова pro centum, что буквально означает «за сотню» или «со ста». Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти».
Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы. Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике.
Ныне процент — это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу). Знак % происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буква t превратилась в наклонную черту (/), возник современный символ для обозначения процента. В школьном учебнике «Математика, 5«,авторов Н.Я. Виленкина и др. дана еще одна любопытная версия возникновения знака %. Там, в частности, говорится, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком. В 1685 г. в Париже была опубликована книга-руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %.
Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост стоимости акций, снижение покупательской способности касаются каждого человека в нашем обществе. Планирование семейного бюджета, выгодного вложения денег в банки, невозможны без умения производить несложные процентные вычисления.
Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость.
В вариантах вступительных экзаменов встречаются задачи на проценты, и эти задачи часто вызывают затруднения у школьников. Причина в том, что тема «Проценты» изучается в младших 5-6 классах, причем непродолжительно, закрепляется в 7 классе при решении задач на повторение, а в старших классах к этой теме совсем не возвращаются.
Так, пересмотрев школьные учебники по математике, по которым обучаются ученики нашей гимназии, я выяснила, что в учебнике «Алгебра, 9», под ред. Теляковского, задач, в которых упоминается слово «процент», всего три. В учебнике «Алгебра и начала анализа, 10-11» под ред Колмогорова А.Н задач на проценты и процентную концентрацию черыре. Но, задачи на проценты уже встречались в вариантах единого государственного экзамена в 2003, 2004, 2005 годах. Предлагается такая задача и в демонстрационном варианте 2007 года. Поэтому, изучение наиболее часто встречающихся типов задач на проценты, считаю актуальным.
Объектом исследования является изучение различных типов задач по теме «Проценты».
Изучая эту тему по сборникам для поступающих в вузы[5], я пришла к мнению, что многие задачи авторы сборников предлагают решать с использованием специальных формул, которых в школьных учебниках 5-6 классов, когда и изучаются эти темы, нет.
Предмет исследования: решение задач на проценты и процентное содержание, концентрацию, смеси и сплавы с преимущественным использованием основных правил действия с десятичными и обыкновенными дробями.
Цель работы. Составить практическое пособие по решению задач на проценты для школьников.
Задачи исследования:
1) Изучить исторический и теоретический материал по интересующему вопросу.
2) Систематизировать задачи на проценты по типам.
3) Составить практические рекомендации по решению задач на проценты.
4) Выявить практическое применение таких задач.
5) Определить план дальнейшей работы над темой.
Практическая значимость работы. Данное пособие по решению задач на проценты будет интересно не только школьникам 5-6 класса, которым интересна математика. Здесь найдут много полезного и выпускники школ, и абитуриенты при подготовке к выпускным и вступительным экзаменам.
Глава 1.Основные типы задач по теме «Проценты»
В данной главе приводятся примеры задач, которые решаются с применением определения, что такое один процент, как выразить дробь в процентах и правилам нахождения части (дроби) от числа, и числа по значению его части (дроби), т.е. это те темы и задачи, которые рассматриваются в школе.
Обращаем внимание, что существуют и другие способы решения простейших задач на проценты, например, составляют пропорции на каждом шаге, но в этом случае решение становится на несколько шагов длиннее. Мы же видим свою задачу в нахождении более быстрых способов решения таких задач, в связи с тем, что в настоящее время редкий тест по математике для абитуриентов, обходится без задач, в которых не упоминались бы проценты.
1.1. Решение задач на применение основных понятий о процентах.
Сотая часть метра — это сантиметр, сотая часть рубля — копейка, сотая часть центнера — килограмм. Люди давно замети, что сотые доли величин удобны в тактической деятельности. Потому для них было придумано специальное название — процент. Значит одна копейка — один процент от одного рубля, а один сантиметр — один процент от одного метра.
Один процент — это одна сотая доля числа. Математическими знаками один процент записывается так: 1%.
Определение одного процента можно записать равенством: 1 % = 0,01 * а
5%=0,05, 23%=0,23, 130%=1,3 и т. д
Как найти 1% от числа? Раз 1% это одна сотая часть, надо число разделить на 100. Деление на 100 можно заменить умножением на 0,01. Поэтому, чтобы найти 1% от данного числа, нужно умножить его на 0,01. А если нужно найти 5% от числа, то умножаем данное число на 0,05 и т.д.
Пример. Найти: 25% от 120.
Ответ: 30.
Правило 1. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь
Пример. Токарь вытачивал за час 40 деталей. Применив резец из более прочной стали, он стал вытачивать на 10 деталей в час больше. На сколько процентов повысилась производительность труда токаря?
Решение: Чтобы решить эту задачу, надо узнать, сколько, процентов составляют 10 деталей от 40. Для этого найдем сначала, какую часть составляет число 10 от числа 40. Мы знаем, что нужно разделить 10 на 40. Получится 0,25. А теперь запишем в процентах — 25%. Получаем ответ: производительность труда токаря повысилась на 25%.
Правило 2. Чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.
Пример. При плановом задании 60 автомобилей в день завод выпустил 66 автомобилей. На сколько процентов завод выполнил план?
Решение: — такую часть составляют изготовленные автомобили от количества автомобилей по плану. Запишем в процентах =110%
Ответ: 110%
Пример.
На сколько процентов 10 больше 6? 2. На сколько процентов 6 меньше 10?
Решение:
1. ((10 — 6).100%)/6 = 66 2/3 %
2. ((10 — 6).100%)/10 = 40%
Ответ: 66 2/3 %, 40 %.
Пример. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
Решение: 1) 6+ 34 =40 (кг) масса всего сплава.
2) = 85% сплава составляет медь.
Ответ. 85%.
Пример. Что произойдет с ценой товара, если сначала ее повысить на 25%, а потом понизить на 25%?
Правило 3. Чтобы найти процентное отношение двух чисел А и В, надо отношение этих чисел умножить на 100%, то есть вычислить (а/в)*100%.
Пример. Найти число, если 15% его равны 30.
Решение:
1) 15% = 0,15;
2) 30 : 0,15 = 200.
или: х — данное число; 0,15.х = 300; х = 200.
Ответ: 200.
Пример. Из хлопка-сырца получается 24% волокна. Сколько надо взять хлопка-сырца, чтобы получить 480кг волокна.?
Решение. Запишем 24% десятичной дробью 0,24 и получим задачу о нахождении числа по известной ему части (дроби). 480 : 0,24= 2000 кг = 2 т
Ответ: 2 т
Пример. Сколько кг белых грибов надо собрать для получения 1 кг сушеных, если при обработке свежих грибов остается 50% их массы, а при сушке остается 10% массы обработанных грибов?
Решение. 1кг сушеных грибов — это 10% или 0, 01 часть обработанных, т.е. 1 кг : 0,1=10 кг обработанных грибов, что составляет 50% или 0,5 собранных грибов, т.е. 10 кг : 0,05=20 кг
Ответ: 20 кг
Ответ: 2,5 кг.
Правило 4. Чтобы найти число по данным его процентам, надо выразить проценты в виде дроби, а затем значение процентов разделить на эту дробь.
1.2. Решение задач на понятия «процентное содержание», «концентрация», «%-й раствор».
Процентное содержание. Процентный раствор.
Пример. Сколько кг соли в 10 кг соленой воды, если процентное содержание соли 15%.
Ответ: 1,5 кг.
Процентное содержание вещества в растворе (например, 15%), иногда называют %-м раствором, например, 15%-й раствор соли.
Пример. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?
Решение: Процентное содержание вещества в сплаве — это часть, которую составляет вес данного вещества от веса всего сплава.
Ответ: 40%, 60%.
Концентрация.
Если концентрация вещества в соединении по массе составляет р%, то это означает, что масса этого вещества составляет р% от массы всего соединения.
Пример. Концентрация серебра в сплаве 300 г составляет 87%. Это означает, что чистого серебра в сплаве 261 г.
В этом примере концентрация вещества выражена в процентах.
Отношения объема чистой компоненты в растворе ко всему объему смеси называется объемной концентрацией этой компоненты.
Сумма концентраций всех компонент, составляющих смесь, равна 1.
Если известно процентное содержание вещества, то его концентрация находится по формуле: К=р/100% к — концентрация вещества; р — процентное содержание вещества (в процентах).
Пример. Имеется 2 сплава, в одном из которых, содержится 40%, а в другом 20% серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?
Ответ: 13 1/3 кг второго сплава нужно добавить к 20 кг первого, чтобы получить сплав, содержащий 32% серебра.
Пример. К 15 л 10%-ного раствора соли добавили 5%-ный раствор соли и получили 8%-ный раствор. Какое количество литров 5%-ного раствора добавили?
Ответ: добавили 10 л 5%-ного раствора
1.3. Решение задач с использованием понятия коэффициента увеличения.
Чтобы увеличить положительное число а на р процентов, следует умножить число а на коэффициент увеличения к=(1+0,01р).
Чтобы уменьшить положительное число а на р процентов, следует умножить число а на коэффициент уменьшения к= (1-0,01р).
Пример. Вклад, вложенный в сбербанк два года назад, достиг суммы, равной 13125 руб. Каков был первоначальный вклад при 25% годовых?
Решение. Если а (рублей) — размер первоначального вклада, то в конце первого года вклад составит 1,25а а в конце второго года размер вклада составит 1,25 *1,25а. Решая уравнение 1,25* 1,25а=13125, находим а=8400.
Ответ: 8400 руб.
Пример. В феврале цена на нефть увеличилась на 12% по сравнению с январской. В марте цена нефти упала на 25%. На сколько процентов мартовская цена изменилась по сравнению с январской?
Решение. Если х — январская цена нефти, то февральская цена нефти равна
Ответ: цена упала на 16%.
Глава 2. Разные задачи на проценты ( с решениями)
В данной главе рассматривается выборка задач из различных источников, которые охватывают весь теоретический материал, который излагался выше, предлагаем свои решения. Отметим, что предложенный способ решения не является единственным.
2.1 Тестовые задания на проценты.
Задача 1.Товар стоил тысячу рублей. Продавец поднял цену на 10%, а через месяц снизил её на 10%.Сколько стал стоить товар?
Решение. Пусть товар стоил 1000руб., после повышения цены на 10% он стал стоить 1,1*1000 руб. После понижения этой цены на 10%, он стал стоить 0,9*1,1*1000=990 руб.
Ответ. 990 руб.
Решение. Так как влажность грибов составляет 99%, это означает, что на так называемое «сухое вещество приходится 1% грибов, т.е 1 кг, после сушки влажность составляет 98%, т.е. на «сухое вещество» приходится 2%, т.е 1кг это 0,02 подсушенных грибов, 1 кг : 0,02=50 кг.
Ответ. 50 кг.
Решение. Пусть зрителей, до понижения цены, на стадион приходило А чел. и выручка составляла 1,8А руб. После понижения цены, цена 1,8*р, зрителей стало 1,5А, выручка составляет 1,8*р*1,5*А руб. С другой стороны, выручка повысилась на 25%, т.е. составляет 1,25*1,8А. Получаем 1,8*р*1,5*А=1,25*1,8А., откуда р=12,5/15, тогда билет стоит 1,8*12,5/15=1,5 руб.
Ответ. 1руб. 50 коп
Задача 4. По дороге идут два туриста. Первый из них делает шаги на 10% короче и в то же время на 10% чаще, чем второй. Кто из туристов идет быстрее и почему?
Решение. Пусть второй турист делает а шагов, каждый из которых равен в, тогда ав это длина пройденного пути. А первый турист тогда прошел1,1*а*0,9*в=0,99*ав, что меньше ав.
Ответ. Второй турист идет быстрее.
Задача 5. Цену за товар уменьшили на 10%, а затем еще на 10%. Стоит ли он дешевле, если цену сразу снизить на 20%?
Ответ. Да.
Задача 6. Числитель дроби увеличили на 20%. На сколько процентов надо уменьшить её знаменатель, чтобы в итоге дробь возросла вдвое?
Ответ. 40%
Задача 7. Матроскин продает молоко через магазин и хочет получать за него 25 рублей за литр. Магазин удерживает 20% стоимости проданного товара. По какой цене будет продаваться молоко в магазине?
Решение. Пусть молоко продает магазин по А руб, тогда после удержания 20% стоимости товара, Матроскину остается 0,8*А=25, откуда А=31, 25 руб.
Ответ. 31 руб. 25 коп.
Задача 8. Один покупатель купил 25% имевшегося куска полотна, второй покупатель 30% остатка, а третий — 40% нового остатка. Сколько (в процентах) полотна осталось непроданным?
Ответ. 31,5%
Задача 9. Бригада косарей в первый день скосила половину луга и еще 2 га, а во второй день 25% оставшейся части и последние 6 га. Найти площадь луга.
Решение. 6 га составляют 75% или0,75=3/4 от оставшейся части после 1 дня работы, т.е.6: 0,75=6 га 8+2=10 га — это половина луга, весь луг 20 га
Ответ. 20 га
Задача 10. Как изменится в процентах площадь прямоугольника, если его длина увеличится на 30%, а ширина уменьшится на 30%?
Решение. АВ- площадь исходного прямоугольника, 1,3*А*0,7*В=0,91АВ — площадь нового прямоугольника, что составляет 91% исходного.
Ответ. Уменьшится на 9%
Задача 11. В драматическом кружке число мальчиков составляет 80% от числа девочек. Сколько процентов составляет число девочек в этом кружке от числа мальчиков?
Решение. Девочек А чел, мальчиков 0,8*А, девочки составляют от мальчиков А/(0,8А)= 1,25, т.е. 125 % от числа мальчиков
Ответ. 125%
Задача 12. В бассейн проведена труба. Вследствие засорения её приток воды уменьшился на 60%. На сколько процентов вследствие этого увеличится время, необходимое для заполнения бассейна
Решение. Пусть Х — объем воды, который должен поступить за время Т при притоке А в ед времени., т.е. Х=АТ. Так как приток уменьшился на 60%, т.е. стал составлять 0,4А, тогда время стало ТК. Получим АТ=0,4А*КТ, откуда К = 2,5, что составляет 250% от времени, необходимого на заполнение бассейна до засорения, т.е. время увеличилось на 150%
Ответ. 150%
Задача 13. 5 литров сливок с содержанием жира 35% смешали с 4 литрами 20%-ных сливок и к смеси добавили 1 литр чистой воды. Какой жирности получилась смесь?
Решение. 0,35*5+0,2*4=р*(5+4+1), откуда р=0,255, что составляет 25,5%
Ответ. 25,5%
2.2. Избранные задачи вариантов единого государственного экзамена.
Впервые в вариантах единого государственного экзамена по математике задача на проценты появились в 2003 году в заданиях группы В, в 2004 и в 2005 годах такие задачи также были представлены в вариантах единого экзамена. В вариантах 2006 года были задачи на работу, но в демонстрационном варианте 2007 года снова появляется задача на проценты, что говорит о необходимости серьезной работы над этой темой. Следует отметить, что для решения всех задач, которые предлагались, достаточно знания тех методов, которые рассматриваются в данной работе.
2003. Тренировочный вариант. Задание В7
Банк предлагает вклад «студенческий». По этому вкладу, сумма, имеющаяся на 1 января, ежегодно увеличивается на одно и то же число процентов. Вкладчик положил 1 января 1000 руб. и в течение 2 лет не производил со своим вкладом никаких операций. В результате вложенная им сумма увеличилась до 1210 руб. На сколько процентов ежегодно увеличивалась сумма денег, положенная на этот вклад?
Решение. Используя формулу увеличения положительного число на p%, получим, что через год сумма вклада составит 1000*(1+0,01р), а через два года 1000*(1+0,01р)2=1210, т.е. (1+0,01р)2=1,21, 1+0,01р=1,1, 0,01р=0,1, откуда р=10%
Ответ: сумма ежегодно увеличивалась на 10%.
2003. Демонстрационный вариант. Задание В7
Владелец дискотеки имел стабильный доход. В погоне за увеличением прибыли он повысил цену на билеты на 25%. Количество посетителей резко уменьшилось, и он стал нести убытки. Тогда он вернулся к первоначальной цене билетов. На сколько процентов, владелец дискотеки снизил новую цену билетов, чтобы она стала равна первоначальной?
Решение. Пусть цена билета была А руб. После повышения на 25% цена стала 1,25А, после понижения цена билета стала р*1,25А. Т.к. цена билета вернулась к первоначальной, то получим р*1,25А=А, откуда р=1/1,25 = 0,8, что означает, что новая цена составляет 80% цены после повышения., значит владелец дискотеки снизил цену на 20%.
Ответ: 20%
2003. ЕГЭ
Предприятие уменьшило выпуск продукции на 20%. На сколько процентов, необходимо теперь увеличить выпуск продукции, чтобы достигнуть его первоначального уровня?
Решение. Пусть А количество продукции, выпускаемое предприятием, 0,8А-количество продукции, которое стало выпускать предприятия после уменьшения на 20%. Из условия задачи следует уравнение р*0,8А=А, где р —коэффициент увеличения, откуда р=1/0,8=1,25, что означает, что необходимо увеличить выпуск продукции на 25%.
Ответ: 25%
2003. ЕГЭ
К 120 г раствора, содержащего 80% соли, добавили 480 г раствора, содержащего 20 % той же соли. Сколько процентов соли содержится в получившемся растворе?
Решение. 1) 0,8*120=96(г)-соли в первоначальном растворе;
2) 480*0,2=96(г) соли во втором растворе;
3) ((96+96)/(120+480))*100%=32%-процентное содержание соли в получившемся растворе.
Ответ: 32%
2003. ЕГЭ
За год стипендия студента увеличилась на 32%. В первом полугодии стипендия увеличилась на 10%. Определить, на сколько процентов увеличилась стипендия во втором полугодии?
Ответ: на 20%.
2004. ЕГЭ
Имеются два слитка сплава золота с медью. Первый слиток содержит 230 г золота и 20 г меди, а второй слиток — 240 г золота и 60 г меди. От каждого слитка взяли по куску, сплавили их и получили 300 г сплава, в котором оказалось 84 % золота. Определить массу ( в граммах) куска, взятого от первого слитка.
Решение. Определим процентное содержание золота в обоих слитках. 1) 230+20=250(г)-масса 1 слитка, 230/250=0,92 (92%)процентное содержание золота в 1 слитке.
2) 240+60=300(г) —масса 2 слитка, 240/300=0,8 (80%)- процентное содержание золота во 2 слитке. Пусть х масса куска, взятого от 1 слитка, (300-х)- масса куска, взятого от 2 слитка, получим уравнение 0,92х+0,8(300-х)=0,84*300, откуда х=100
Ответ: 100г.
2004 ЕГЭ
Первый сплав серебра и меди содержит 70 г меди, а второй сплав — 210 г серебра и 90 г меди. Взяли 225 г первого сплава и кусок второго сплава, сплавили их и получили 300 г сплава, который содержит 82 % серебра. Сколько граммов серебра содержалось в первом сплаве?
Решение. Пусть х г серебра содержится в 1 сплаве., тогда 70/(х+70)-какую часть 1 сплава составляет медь, 90/(210+90)-такую часть составляет медь во 2 сплаве., кусок второго сплава 300-225=75г, тогда получаем уравнение.
225*(70/(х+70))+75*(90/300)=(1-0,82)*300, откуда х=430г
Ответ: 430г
ЕГЭ 2004
Решение. 200*0,8=160(г)-масса чистого спирта в колбе, их колбы отлили х г раствора, осталось (200-х)г раствора, в котором чистого спирта 0,8*(200-х). Когда к раствору добавили х г воды, то масса раствора снова стала 200 г, а концентрация
[(0,8*(200-х))/200]*100%=60%, откуда х=50(г).
Ответ: провизор добавил 50г воды.
ЕГЭ 2004
Решение. После того, как провизор отлил 200 г раствора, стало 600г, в котором чистого спирта 0,8*600=480г, когда добавили200г воды, то раствор снова 800г, а концентрация чистого спирта в растворе (480/800)*100%=60%
Ответ: 60%
ЕГЭ 2005
Численность населения в городе Таганроге в течение двух лет возрастала на 2 процента ежегодно. В результате число жителей возросло на 11312 человек. Сколько жителей было в Таганроге первоначально?
Решение. А- первоначальное количество жителей Таганрога. Используя формулу коэффициента увеличения, получаем
А(1+0,02)2=А+11312, откуда А=280000
Ответ: 280000 чел
ЕГЭ 2005
Решение. Пусть х л вмещает сосуд, тогда из условий задачи следует уравнение 0,94(х-1,5)+0,7*1,5=0,86х, откуда х=4,5 л.
Ответ: 4,5 л
Демонстрационный вариант 2007
Денежный вклад в банк за год увеличивается на 11 %. Вкладчик внес в банк 7000 рублей. В конце первого года он решил увеличить сумму вклада и продлить срок действия договора еще на год, чтобы в конце второго года иметь на счету не менее 10000 рублей. Какую наименьшую сумму необходимо дополнительно положить на счет по окончании первого года, чтобы при той же процентной ставке (11 %) реализовать этот план? (Ответ округлите до целых.)
Решение. 1,11* 7000=7770руб-будет на счете в конце 1 года. Пусть х руб. положили дополнительно на счет, из условия задачи получаем неравенство 1,11(7770+х)> 10000, получим х>1239, 1/111, что означает, чтобы на счету было не менее 10000 руб, нужно положить не менее12 40руб.
Ответ: 1240 руб.
Заключение
Данное практическое пособие позволит развить и закрепить навыки решения задач по теме: «Проценты» у учащихся 5-6 классов, может быть интересно учащимся, увлеченным математикой, а также полезно выпускникам школ и абитуриентам при подготовке к экзаменам. В дальнейшем на факультативных и кружковых занятиях возможны изучение вопроса применения процентов в экономике, в банковском деле. Можно провести сравнительный анализ банковских процентных ставок по потребительским кредитам и ипотечному кредитованию населения.
Литература
2.Денищева Л.О., Глазков Ю.А. и др., Учебно-тренировочные материалы для подготовки к ЕГЭ. Математика, М: Интеллект- Центр, 2003.
3. Потапов М.К., Олехник С.Н., Нестеренко Ю.В., Конкурсные задачи по математикеМ: Наука, 1992.
4. Семенко Е.А. и др., Готовимся к ЕГЭ по математике, Краснодар, Просвещение-Юг, 2005.
5. Алгебра, 9, под ред. Теляковского С.А., М: Просвещение, 2001
6. Алгебра и начала анализа, 10-11, под ред. Колмогорова А.Н., М: Просвещение, 2003.
7. Математика. Контрольные измерительные материалы единого государственного экзамена в 2004 г. М: Центр тестирования, 2004.
8. Экзаменационные материалы для подготовки к единому государственному экзамену. ЕГЭ 2006, М: Центр тестирования, 2005.
[1] «Математика, 5», Виленкин Н.Я. и др., «Мнемозина», 2003, с. 337
[2] «Алгебра, 9», под ред. Теляковского С.А., М: Просвещение, 2001, с.215, 223
[3] «Алгебра и начала анализа, 10-11», под ред. Колмогорова А.Н., М: Просвещение, 2003, с.306,330.
[4] «Учебно-тренировочные материалы для подготовки к ЕГЭ. Математика», Денищева Л.О., Гдазков Ю.А. и др., М: Интеллект- Центр, 2003.
«Математика. Контрольные измерительные материалы единого государственного экзамена в 2004 г.» М: Центр тестирования, 2004.
«Экзаменационные материалы для подготовки к единому государственному экзамену. ЕГЭ 2006», М: Центр тестирования, 2005.
[5] «Конкурсные задачи по математике», Потапов М.К., Олехник С.Н., Нестеренко Ю.В., М: Наука, 1992, с330-332.
«В помощь поступающим в ГУ — ВШЭ, Математика», Быков А.А. и дрМ: ГУ-ВШЭ, 2004, с 53-64
«Готовимся к ЕГЭ по математике», Семенко Е.А. и др., Краснодар, Просвещение-Юг, 2005, с. 46-51