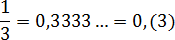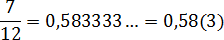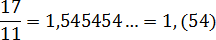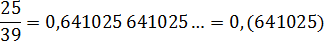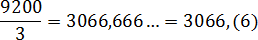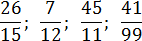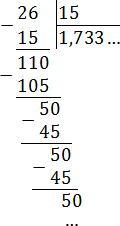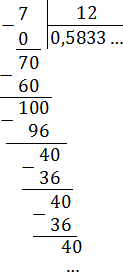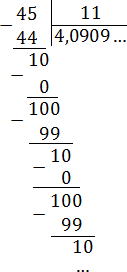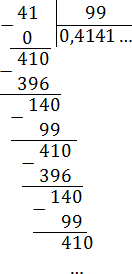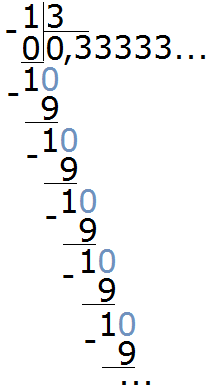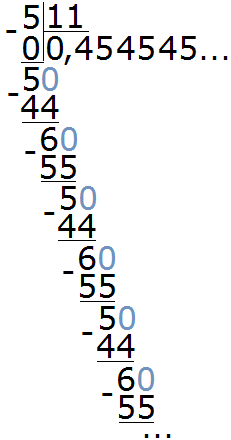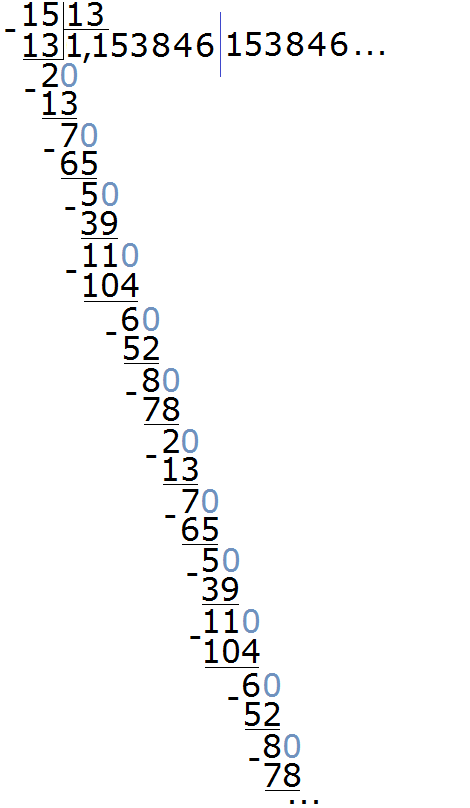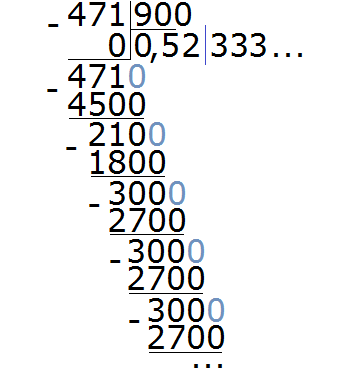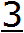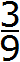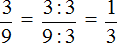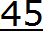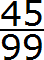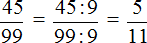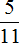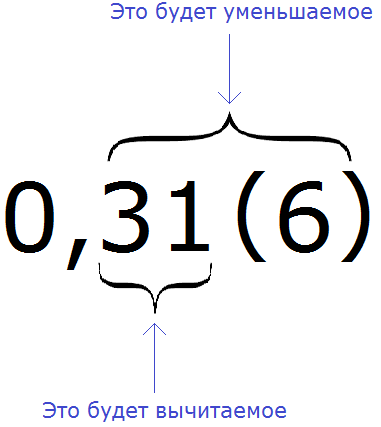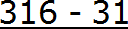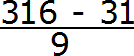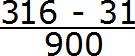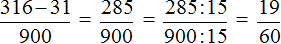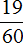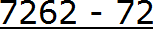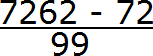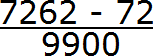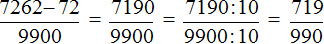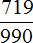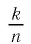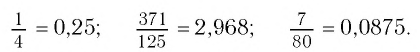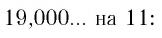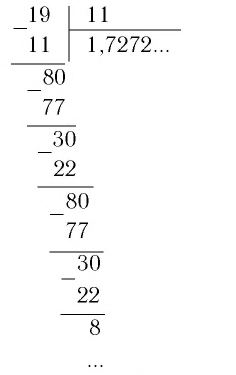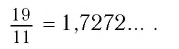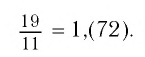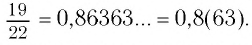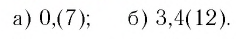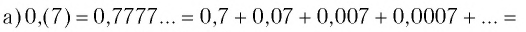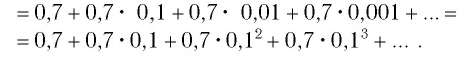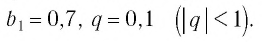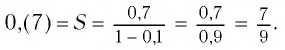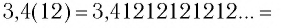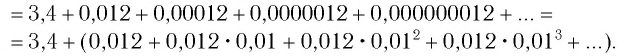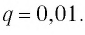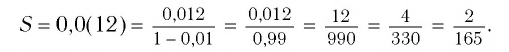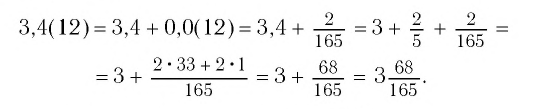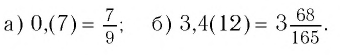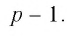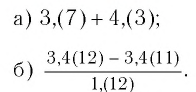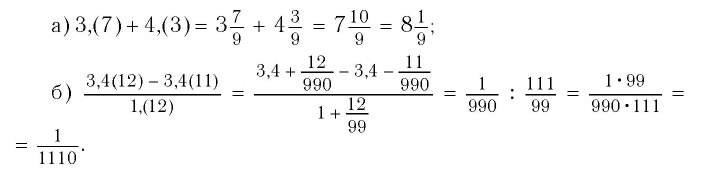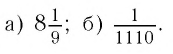Как решить периодическую дробь
Периодические десятичные дроби
Помните, как в самом первом уроке про десятичные дроби я говорил, что существуют числовые дроби, не представимые в виде десятичных (см. урок «Десятичные дроби»)? Мы еще учились раскладывать знаменатели дробей на множители, чтобы проверить, нет ли там чисел, отличных от 2 и 5.
Так вот: я наврал. И сегодня мы научимся переводить абсолютно любую числовую дробь в десятичную. Заодно познакомимся с целым классом дробей с бесконечной значащей частью.
— это любая десятичная дробь, у которой:
Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:
Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.
Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.
Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.
Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.
Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.
Как видите, определение периодической дроби основано на понятии значащей части числа. Поэтому если вы забыли что это такое, рекомендую повторить — см. урок «Умножение и деление десятичных дробей».
Переход к периодической десятичной дроби
Рассмотрим обыкновенную дробь Разложим ее знаменатель на простые множители. Возможны два варианта:
Чтобы задать периодическую десятичную дробь, надо найти ее периодическую и непериодическую часть. Как? Переведите дробь в неправильную, а затем разделите числитель на знаменатель «уголком».
При этом будет происходить следующее:
Вот и все! Повторяющиеся цифры после десятичной точки обозначаем периодической частью, а то, что стоит спереди — непериодической.
Задача. Переведите обыкновенные дроби в периодические десятичные:
Все дроби без целой части, поэтому просто делим числитель на знаменатель «уголком»:
Как видим, остатки повторяются. Запишем дробь в «правильном» виде:
В итоге получается дробь:
Записываем в нормальном виде:
Переход от периодической десятичной дроби к обыкновенной
Рассмотрим периодическую десятичную дробь Требуется перевести ее в классическую «двухэтажную». Для этого выполним четыре простых шага:
Задача. Приведите к обыкновенной неправильной дроби числа:
Работаем с первой дробью:
В скобках содержится лишь одна цифра, поэтому период Далее умножаем эту дробь Имеем:
Вычитаем исходную дробь и решаем уравнение:
Теперь разберемся со второй дробью. Итак,
Период k = 2, поэтому умножаем все
Снова вычитаем исходную дробь и решаем уравнение:
100 X − X =
99 X = 3207;
X = 3207/99 = 1069/33.
Приступаем к третьей дроби: Схема та же самая, поэтому я просто приведу выкладки:
Период k = 1 ⇒ умножаем все на 10 k = 10 1 = 10;
Наконец, последняя дробь: Опять же, для удобства периодические части отделены друг от друга пробелами. Имеем:
Периодические дроби
Существуют дроби, у которых в дробной части некоторые цифры бесконечно повторяются. Выглядят эти дроби следующим образом:
Дроби такого вида называют периодическими. В данном уроке мы попробуем разобраться, что это за дроби и как с ними работать.
Получаем периодическую дробь
Попробуем разделить 1 на 3. Не будем подробно останавливаться на том, как это сделать. Этот момент подробно описан в уроке действия с десятичными дробями, в теме деление меньшего числа на большее. Продвинутый уровень.
Видно, что мы постоянно получаем остаток 1, далее приписываем к нему 0 и делим 10 на 3. И это повторяется вновь и вновь. В результате в дробной части каждый раз получается цифра 3. Деление 1 на 3 будет выполняться бесконечно, поэтому разýмнее будет остановиться на достигнутом.
Такие дроби называют периодическими, поскольку у них присутствует период цифр, который бесконечно повторяется. Период цифр может состоять из нескольких цифр, а может состоять из одной как в нашем примере.
В примере, который мы рассмотрели выше, период в дроби 0,33333 это цифра 3. Обычно такие дроби записывают сокращённо. Сначала записывают цéлую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).
В нашем примере повторяется цифра 3, она является периодом в дроби 0,33333. Поэтому сокращённая запись будет выглядеть так:
Читается как «ноль целых и три в периоде»
Пример 2. Разделить 5 на 11
Это тоже периодическая дробь. Период данной дроби это цифры 4 и 5, эти цифры повторяются бесконечно. Сокращённая запись будет выглядеть так:
Читается как «ноль целых и сорок пять в периоде»
Пример 3. Разделить 15 на 13
Здесь период состоит из нескольких цифр, а именно из цифр 153846. Для наглядности период отделён синей линией. Сокращённая запись для данной периодической дроби будет выглядеть так:
Читается как: «одна целая сто пятьдесят три тысячи восемьсот сорок шесть в периоде».
Пример 4. Разделить 471 на 900
В этом примере период начинается не сразу, а после цифр 5 и 2. Сокращённая запись для данной периодической дроби будет выглядеть так:
Читается как: «ноль целых пятьдесят две сотых и три в периоде».
Виды периодических дробей
Периодические дроби бывают двух видов: чистые и смéшанные.
Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют чистой. Например, следующие периодические дроби являются чистыми:
Видно, что в этих дробях период начинается сразу после запятой.
Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют смéшанной. Например, следующие периодические дроби являются смéшанными:
Видно, что в этих дробях период начинается не сразу, а после некоторого количества не повторяющихся цифр.
Избавляемся от хвоста
Подобно тому, как ящерица избавляется от хвоста, мы можем избавить периодическую дробь от повторяющегося периода. Для этого достаточно округлить эту периодическую дробь до нýжного разряда.
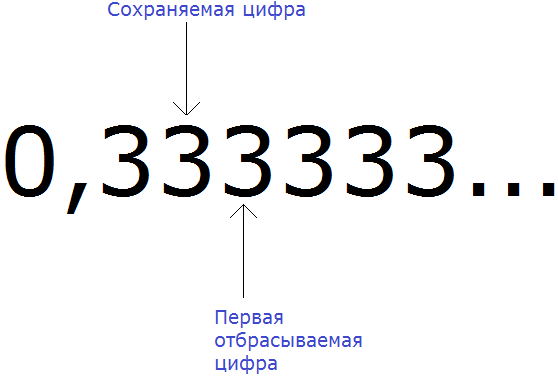
Например, округлим периодическую дробь 0, (3) до разряда сотых. Чтобы увидеть сохраняемую и отбрасываемую цифру, временно запишем дробь 0, (3) не в сокращённом виде, а в полном:
Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит периодическая дробь 0, (3) при округлении до сотых обращается в дробь 0,33
Округлим периодическую дробь 6,31 (6) до разряда тысячных.
Запишем эту дробь в полном виде, чтобы увидеть сохраняемую и отбрасываемую цифру:
Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит периодическая дробь 6,31 (6) при округлении до тысячных обращается в дробь 6,317
Перевод чистой периодической дроби в обыкновенную дробь
Перевод периодической дроби в обыкновенную это операция, которую мы будем применять довольно редко. Тем не менее, для общего развития желательно изучить и этот момент. А начнём мы с перевода чистой периодической дроби в обыкновенную дробь.
Мы уже говорили, что если период в периодической дроби начинается сразу после запятой, то такую дробь называют чистой.
Чтобы перевести чистую периодическую дробь в обыкновенную дробь, нужно в числитель обыкновенной дроби записать период периодической дроби, а в знаменатель обыкновенной дроби записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби.
В качестве примера, рассмотрим чистую периодическую дробь 0, (3) — ноль целых и три в периоде. Попробуем перевести её в обыкновенную дробь.
Правило гласит, что в первую очередь в числитель обыкновенной дроби нужно записать период периодической дроби.
Итак, записываем в числителе период дроби 0, (3) то есть тройку:
А в знаменатель нужно записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (3).
В периодической дроби 0, (3) период состоит из одной цифры 3. Значит в знаменателе обыкновенной дроби записываем одну девятку:
Полученную дробь 
можно сократить на 3, тогда получим следующее:
Получили обыкновенную дробь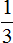 
.
Таким образом, при переводе периодической дроби 0, (3) в обыкновенную дробь получается
Пример 2. Перевести периодическую дробь 0, (45) в обыкновенную дробь.
Здесь период составляет две цифры 4 и 5. Записываем эти две цифры в числитель обыкновенной дроби:
А в знаменатель записываем некоторое количество девяток. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (45).
В периодической дроби 0, (45) период состоит из двух цифр 4 и 5. Значит в знаменателе обыкновенной дроби записываем две девятки:
Полученную дробь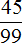 
можно сократить эту дробь на 9, тогда получим следующее:
Таким образом, при переводе периодической дроби 0, (45) в обыкновенную дробь получается 
Перевод смешанной периодической дроби в обыкновенную дробь
Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно в числителе записать разность в которой уменьшаемое это цифры, стоящие после запятой в периодической дроби, а вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.
В знаменателе же нужно записать некоторое количество девяток и нулей. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби, а количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
Например, переведём смешанную периодическую дробь 0,31 (6) в обыкновенную дробь.
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,31 (6)
В дроби 0,31 (6) период состоит из одной цифры. Значит в знаменатель дроби записываем одну девятку:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,31 (6) между запятой и периодом располагается две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ 
Таким образом, при переводе периодической дроби 0,31 (6) в обыкновенную дробь, получается
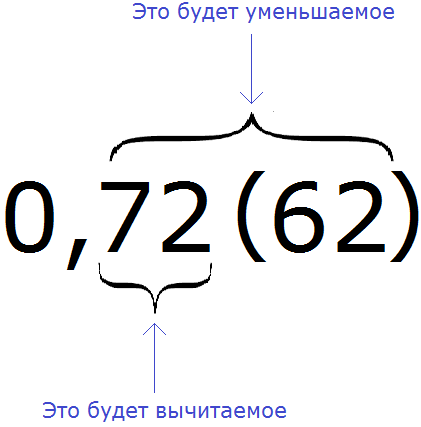
Пример 2. Перевести смешанную периодическую дробь 0,72 (62) в обыкновенную дробь
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,72 (62)
В дроби 0,72 (62) период состоит из двух цифр. Значит в знаменатель дроби записываем две девятки:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,72 (62) между запятой и периодом располагаются две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ 
Значит при переводе периодической дроби 0,72 (62) в обыкновенную дробь, получается
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
34 thoughts on “Периодические дроби”
Когда же следующие уроки? Уже что-то долго ничего нету
Большое спасибо за урок! Откровенно говоря…эту тему не помню вообще…Будто ее и не было в школе О__о Ну или я ее проболела… (Перевод смешанной периодической дроби в обыкновенную дробь)
Вы бы хоть номер кошелька написали. А то столько трудились и никакой отдачи. С такими уроками никакой экзамен не страшен.
Спасибо большое Тэла, за столь добрый отзыв 😉
Если люди получают пользу от этих уроков — это уже отдача)
Огромное Вам спасибо за уроки! Всё объясняете доступно и наглядно! На ваших уроках готовлюсь поступать на ФИТ на программиста. Хорошо бы еще алгебру выложили.)
Вы не могли бы объяснить логику алгоритма перевода периодической дроби в обычную?
Зачем в знаменателе ставятся девятки — заместно, например, округления числа, подставляемого в числитель, до последней цифры периода, и постановки степени 10 в знаменатель? Зачем, при переводе смешанной периодической дроби, производится соотв. вычитание и чем объясняется подстановка нулей и единиц в зависимости от принадлежности цифры к периоду??…
Спасибо большое за урок 🙂 Скажите пожалуйсто при округлении(когда избавляемся от хвоста) откуда знать до каких разряд надо округлять?
Вот и здесь последняя задача говорит округлить до разряда сотых,а почему не до десятых(например)?
зависит от задачи, которую решаете. Если в задаче сказано округлять до десятых, значит округляете до десятых. Если сказано округлять до сотых — округляете до сотых
Бесконечные периодические десятичные дроби
В данной публикации мы рассмотрим, что из себя представляют бесконечные периодические десятичные дроби, какие бывают виды, и как их можно перевести в обыкновенную дробь. Также разберем примеры для закрепления материала.
Периодические десятичные дроби
Определение
Если в дробной части бесконечной десятичной дроби есть один или несколько цифр, которые повторяются в одной и той же последовательности, такая дробь является периодической.
Примеры периодических десятичных дробей:
Запись
Повторяющаяся цифра/цифры – это период дроби, который пишется в скобке для сокращения длины записи. Например, дроби выше сокращенно следует писать так:
Произношение
Чистые периодические дроби – это такие бесконечные десятичные дроби, период которых начинается сразу после запятой.
Смешанные периодические дроби – бесконечные десятичные дроби, у которых между запятой и периодом присутствует одна и более цифр (их количество ограничено).
Перевод периодической десятичной дроби в обыкновенную
Для того, чтобы перевести периодическую дробь в обыкновенную (простую), выполняем следующие шаги:
Пример 1
Давайте переведем число 0,8(3) в обыкновенную дробь.
Действовать будет пошагово согласно инструкции выше:
1. n = 1
2. m = 1
3. a = 83
4. b = 8
5. x = 0
6. Остается только применить формулу:
Пример 2
Представим периодическую дробь 2,64(378) в виде обыкновенной.
1. n = 3
2. m = 2
3. a = 64378
4. b = 64
5. x = 2
6. Подставляем эти значения в формулу нахождения простой дроби и получаем:
Периодические дроби с примерами решения
Каждое рациональное число является действительным числом, а поэтому может быть записано в виде десятичной дроби — конечной или бесконечной. Хорошо известно, как это делается, когда 
Применим теперь этот метод обращения обыкновенной дроби в десятичную к числу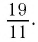 
Для этого разделим 
Таким образом, 
Бесконечная дробь, стоящая в правой части этого равенства, содержит периодически повторяющуюся группу цифр 72. Эта группа цифр называется периодом дроби, а сама дробь — периодической. При записи таких дробей период заключают в скобки и пишут один раз:
(Читается: «Одна целая семьдесят два в периоде».)
Еще один пример: 
(Читается: «Нуль целых восемь десятых шестьдесят три в периоде».)
Приписывая к конечной десятичной дроби бесконечно много нулей, мы получаем бесконечную десятичную дробь. Поэтому конечные десятичные дроби тоже считаются периодическими с периодом 0. (При делении двух натуральных чисел не могут получиться дроби с числом 9 в периоде, поэтому в школьном курсе алгебры их не рассматривают.)
Приведенные примеры дают возможность догадаться, что каждое рациональное число записывается в виде бесконечной десятичной периодической дроби.
Чтобы в этом убедиться, заметим, что для обращения обыкновенной дроби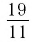 
в десятичную мы на каждом шаге остаток от деления (он был равен либо 8, либо 3) умножали на 10 и делили на 11. Но при делении на 11 вообще возможны лишь 11 различных остатков. Значит, на каком-то шаге остаток обязательно повторится (в нашем примере это случилось на третьем шаге), и поэтому в результате деления должна получиться периодическая дробь.
Наоборот, каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число.
Каждую периодическую десятичную дробь можно рассматривать либо как сумму бесконечно убывающей геометрической прогрессии, либо как сумму конечной десятичной дроби и сумму бесконечно убывающей геометрической прогрессии. Это позволяет представлять периодические десятичные дроби в виде обыкновенных дробей.
Пример №1
Обратить в обыкновенную дробь число:
Решение:
Таким образом, число 0,(7) есть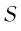 
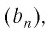
— сумма бесконечно убывающей геометрической прогрессии 
где 
Значит, 
б) 
Сумму, стоящую в скобках, обозначим буквой S. Тогда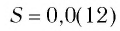 
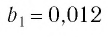
есть сумма бесконечно убывающей геометрической прогрессии с первым членом 
и знаменателем 
Значит, 
Ответ: 
Изучением периодических дробей занимался великий немецкий математик К- Ф. Гаусс (1777—1855). Уже в детстве он делил единицу на все подряд простые числа р из первой тысячи. При этом Гаусс подметил, что, начиная с какого-то места, десятичные знаки начинают повторяться, т. е. получаются периодические десятичные дроби. А периоды некоторых дробей достигали нескольких сотен десятичных знаков. Рассматривая эти примеры, Гаусс установил, что число цифр в периоде всегда является делителем числа 
Пример №2
Найти значение выражения:
Решение:
Обратив каждое из чисел в обыкновенную дробь (см. пример 1), получим: 
Ответ: 
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.