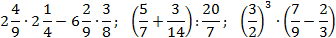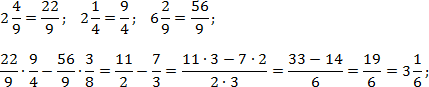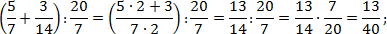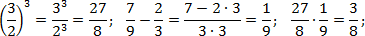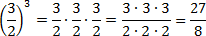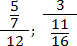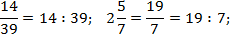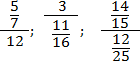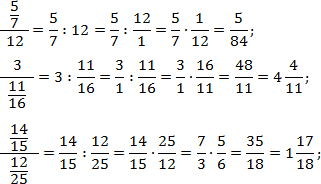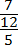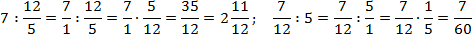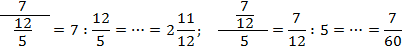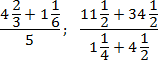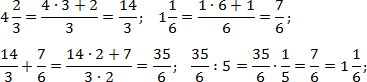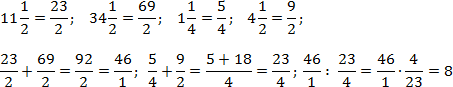Как решить многоэтажную дробь


В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:
Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:
Обратите внимание! В делении дробей очень важен порядок деления.
Будьте внимательны, здесь легко запутаться. Обратите внимание, например:
При делении единицы на любую дробь, результатом будет та же самая дробь, только перевернутая:
Если пример содержит только действия II ступени, то их удобно выполнить под одной дробной чертой.
При вычислениях многоэтажных дробей часто удобно числитель и знаменатель записать в виде натуральных чисел. Для этого надо:
1) Найти НОК знаменателей в выражении многоэтажной дроби;
2) числитель и знаменатель многоэтажной дроби умножить на НОК их знаменателей, в результате записать числитель и знаменатель дроби целыми числами;
3) выполнить действия над целыми числами.
Образец: переход к натуральным числам

1) 


2) 
Пример (1) проще решить по действиям.
В примере (2) НОК находят устно, расставляют доп. множители, выполняют действия с натуральными числами по условию.
1. 1) 






2. 1) 






3. 1) 






4. 1) 





6. 1) 1 + 



Урок в 6-м по теме «Многоэтажные дроби»
Разделы: Математика
Оборудование: интерактивная доска, сканер, карточки с заданием.
Оформление доски: на доске висит картинка, закрытая полосками.
Тип урока: урок – игра.
Ход урока
1. Организационный момент.
Каждый ученик на “шкале настроения” указывает уровень своего настроения от – 5 до +5 баллов.
Настроение класса в начале урока – среднее 1,8 баллов.
Учитель объясняет, в какой форме будет проходить урок и правила игры “Открой картинку”.
Экспертная группа, состоящая из присутствующих гостей, на каждом этапе урока оценивает каждого ученика и выводит средний балл группе.
2. Фронтальный опрос.
Учитель проводит опрос с использованием интерактивной доски (функция “шторка”)
Эксперты озвучивают результаты фронтального опроса.
3. Решение упражнений из учебника №44(а,в), №45(а,б), №46(а,в) .
Решение должно быть аккуратным, так как оно будет сканироваться, и проектироваться на интерактивную доску.
4. Гимнастика для глаз.
5. Игра “Открой картинку” (см. приложение)
Каждая группа получает карточку с заданием. Выполнив задание и выбрав правильный ответ, группа открывает часть картинки. Эксперты озвучивают результаты игры.
Вычислить: 1) 
2) 
3) 


4) 


5) 



6. Творческое задание.
Придумайте задачу, которая бы решалась с помощью следующего дробного выражения:
Эксперты озвучивают результаты творческого задания и общий результат.
7. Подведение итогов.
Каждый ученик получает оценку за урок, которую выставили эксперты. И члены группы – лидера получают дополнительную оценку.
8. Рефлексия:
Ребята оценивают свое настроение по окончании урока.
Настроение класса в конце урока – среднее 3,4 балла. Видно, что настроение у ребят повысилось на 3,4 – 1,8 = 1,6 балла.
Сложные выражения с дробями. Порядок действий
Теперь, когда мы научились складывать и умножать отдельные дроби, можно рассматривать более сложные конструкции. Например, что, если в одной задаче встречается и сложение, и вычитание, и умножение дробей?
В первую очередь, надо перевести все дроби в неправильные. Затем последовательно выполняем требуемые действия — в том же порядке, как и для обычных чисел. А именно:
Разумеется, если в выражении присутствуют скобки, порядок действий изменяется — все, что стоит внутри скобок, надо считать в первую очередь. И помните о неправильных дробях: выделять целую часть надо лишь тогда, когда все остальные действия уже выполнены.
Задача. Найдите значения выражений:
Переведем все дроби из первого выражения в неправильные, а затем выполним действия:
Обратите внимание на последний пример. Чтобы возвести дробь в степень, надо отдельно возвести в эту степень числитель, и отдельно — знаменатель.
Можно решать по-другому. Если вспомнить определение степени, задача сведется к обычному умножению дробей:
Многоэтажные дроби
До сих пор мы рассматривали лишь «чистые» дроби, когда числитель и знаменатель представляют собой обыкновенные числа. Это вполне соответствует определению числовой дроби, данному в самом первом уроке.
Но что, если в числителе или знаменателе разместить более сложный объект? Например, другую числовую дробь? Такие конструкции возникают довольно часто, особенно при работе с длинными выражениями. Вот пара примеров:
Правило работы с многоэтажными дробями всего одно: от них надо немедленно избавляться. Удалить «лишние» этажи довольно просто, если вспомнить, что дробная черта означает стандартную операцию деления. Поэтому любую дробь можно переписать следующим образом:
Пользуясь этим фактом и соблюдая порядок действий, мы легко сведем любую многоэтажную дробь к обычной. Взгляните на примеры:
Задача. Переведите многоэтажные дроби в обычные:
В каждом случае перепишем основную дробь, заменив разделительную черту знаком деления. Также вспомним, что любое целое число представимо в виде дроби со знаменателем 1. Получаем:
В последнем примере перед окончательным умножением дроби были сокращены.
Специфика работы с многоэтажными дробями
В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:
Это выражение можно прочитать по-разному:
Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:
Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно — в несколько раз.
Если следовать этому правилу, то приведенные выше дроби надо записать так:
Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок — пара примеров, где действительно возникают многоэтажные дроби:
Задача. Найдите значения выражений:
Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:
Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:
Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили в форме дроби, чтобы выполнить деление.
Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем — частное.
Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.
Урок на тему: » Многоэтажные дроби»
Тема: «Многоэтажные дроби».
повторить алгоритмы сложения, вычитания, умножения и деления обыкновенных дробей;
познакомить с многоэтажной дробью;
развивать логическое мышление, способности к обобщению, исследовательские умения, речь.
Тип урока: объяснение нового материала.
Проверка домашнего задания: №802, №807
— Назовите числа, обратные данным числам:
3/14, 7/6, 1/2, 8, 90, 1 2/3, 3 4/5, а/в, 1/к, п.
— При каких значениях переменной верно равенство:
— Найдите чему равен х:
Несократимая дробь, у которой числитель и знаменатель оба делятся на 3
Несократимая дробь, у которой числитель делится на 3, а знаменатель не делится на 3
Какая из сумм лишняя?
Смекалкин задал младшему брату задачу: «Дробь равна своему числителю. Чему равен её знаменатель? » Отгадай эту задачу
Младший брат, отгадав загадку, Смекалкина придумал похожую задачу: «Дробь равна своему знаменателю. Чему равен её числитель?»
Доп. вопрос: Мама поручила Игорю купить полбуханки хлеба. По просьбе пожилой соседки, которой трудно дойти до магазина, он купил ещё четверть буханки. Сколько всего хлеба купил Игорь?
IV . Письменная проверка знаний учащихся 1-го ряда, работают по тестам во время устной работы.
Тест по теме «Раскрытие скобок. Коэффициент. Подобные слагаемые»
1. Если перед скобками стоит знак «+», то :
а) знаки всех слагаемых в скобках меняются на противоположные;
б) знаки всех слагаемых в скобках не изменяются.
2. Если перед скобками стоит знак «-», то :
а) знаки всех слагаемых в скобках меняются на противоположные;
б) знаки всех слагаемых в скобках не изменяются.
3. Если выражение является произведением числа и одной или нескольких букв, то это число называют:
а) подобным слагаемым;
4. Слагаемые имеющие одинаковую буквенную часть называются _________
5. Что нужно сделать, чтобы сложить (привести) подобные слагаемые ______
6. Раскройте скобки и найдите значение выражения:
а) – 0,6 + (-4,4 + 3,8) = б) – 1,8 – (- 4,8 + 2,9) = в)
7. Приведите подобные слагаемые:
а) 3х + 15у – 2х – 20у + 7х = б)
8. Упростите выражение и подчеркните коэффициент:
Мы умеем выполнять все действия с обыкновенными дробями. Нам встречались и примеры с несколькими действиями. А вот я встретилась с необычным примером и дома не смогла его решить. Помогите мне.
Выполнение номеров №821, № 822, №823, №824
7
7*(
2.Найдите площадь квадрата, если длина его стороны 1 
3.Реши уравнение
4. Среди дробей 17/15, 21/23, 15/19, 7/14, найдите наибольшую обратную дробь.
5. Какое расстояние пройдёт автомобиль за 5/12 ч, если его скорость 48 км/ч.
I Х . Подведение итога урока. Выставление оценок.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-157691
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
В Петербурге школьникам разрешили уйти на каникулы с 25 декабря
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
НИУ ВШЭ откроет первую в России магистратуру по управлению низкоуглеродным развитием
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Время чтения: 2 минуты
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.