Как решить логическое выражение
Законы алгебры логики и правила преобразования логических выражений
Законы алгебры логики и правила преобразования логических выражений
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Закон
Формулировка
Всякое высказывание тождественно самому себе.
2. Закон исключенного третьего
Высказывание может быть либо истинным, либо ложным, третьего не дано. Следовательно, результат логического сложения высказывания и его отрицания всегда принимает значение «истина».
3. Закон непротиворечия
Высказывание не может быть одновременно истинным и ложным. Если высказывание Х истинно, то его отрицание НЕ Х должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно.
4. Закон двойного отрицания
Если дважды отрицать некоторое высказывание, то в результате получим исходное высказывание.
5. Переместительный (коммутативный) закон
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
6. Сочетательный (ассоциативный) закон
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
5. Распределительный (дистрибутивный) закон
(X /\ Y) \/ Z= (X /\ Z) \/ (Y /\ Z)
(X /\ Y) \/ Z = (X \/ Z) /\ (Y \/ Z)
Определяет правило выноса общего высказывания за скобку.
7. Закон общей инверсии Закон де Моргана
Закон общей инверсии.
8. Закон равносильности (идемпотентности)
от латинских слов idem — тот же самый и potens —сильный
9. Законы исключения констант:
10. Закон поглощения:
11. Закон исключения (склеивания):
12. Закон контрапозиции
14. А В = (А /\ В) \/ (¬A /\ ¬B);
Применим законы алгебры логики. Покажем на примере как можно упростить логическое выражение:
1) (A/\B) \/ (A/\¬B) = A /\ (B \/ B)= A /\ 1 = A
Законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами.
¬ (X \/ Y) /\ (X /\ ¬Y) = ¬ X /\ ¬Y /\ (X /\ ¬Y) = ¬ X /\ X/\¬Y /\¬Y= 0 ¬Y /\¬Y
3) применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией
4) ¬ X /\ Y \/ ¬ (X \/ Y) \/ X = ¬ X /\ Y \/ ¬ X /\ ¬Y \/ X= ¬ X /\ (Y \/ ¬Y) \/ X= ¬ X \/ X= 1
Примеры решения задач «Логические функции»
Примеры решения задач «Логические функции»
Запишите в виде логической формулы следующие высказывания:
1. Если Иванов здоров и богат, то он здоров.
2. Число является простым, если оно делится только на единицу и само на себя.
Решение:
1.Нам дано сложное составное высказывание. Выделим из него простые высказывания:
Запишем высказывание в виде логической формулы A/\B=>A
2. Нам дано сложное составное высказывание. Выделим из него простые высказывания:
А = «Число является простым»
В = «Число делится только на единицу»
С=«Число делится на само себя»
Запишем высказывание в виде логической формулы B/\C=>A
Для какого имени истинно высказывание:
¬ (Первая буква имени гласная => Четвертая буква имени согласная)?
1) Елена 2) Вадим 3) Антон 4) Федор
Решение:
По условию задачи функция F(A, B) истинна, следовательно, отрицание этой функции – ложно, т.е. высказывание (A => B) – ложно. Полученное высказывание является импликацией и ложно только в том случае, когда выражение А истинно, а В — ложно (см. табл. истинности импликации). Следовательно, среди предложенных ответов следует искать тот, в котором первая буква имени гласная и четвертая буква имени также гласная. Этому условию удовлетворяет только имя АНТОН.
Ответ: 3
Для какого числа X истинно высказывание X>1 /\ ((X (X
Решение:
По условию задачи F(A, B) истинна, следовательно, выражения А и В тоже должны быть истинны (см.табл.истинности конъюнкции), т.е.
Рассмотрим предложенные ответы, подставляя значения Х в неравенства и проверяя истинность полученных высказываний:
Ответ 1): 1 > 1 – ложь, что противоречит первому условию;
Ответ 2): 2 > 1 – истина, первое условие совпадает,
(2 (2 => (истина), что является истиной (см. табл. истинности импликации). Т. е. второе условие также совпадает;
Ответ 3): 3 > 1 – истина, первое условие совпадает,
(3 (3 => (ложь), что является ложью (см. табл. истинности импликации), это противоречит второму условию;
Ответ 4): 4 > 1 – истина, первое условие совпадает,
(4 (4 => (ложь), что является ложью (см. табл. истинности импликации), это противоречит второму условию
Примеры решения задач «Алгебра высказываний»
Примеры решения задач «Алгебра высказываний»
Определите значения следующих логических переменных:
1) А = « Два умножить на два равно пяти»
2) В = «Всякий квадрат есть параллелограмм»
3) С = «Всякий параллелограмм есть квадрат»
Ответ: А =0, В = 1, С = 0
Определите значение истинности следующих высказываний:
1) Высказывание «10 делится на 2 и 5 больше 3»
2) Высказывание «10 делится на 2 и 5 не больше 3»
3) Высказывание «10 не делится на 2 и 5 больше 3»
4) Высказывание «10 не делится на 2 и 5 не больше 3»
Ответ:
1) истинное высказывание (1/\1=1)
2) ложное высказывание(1/\0=0)
3) ложное высказывание (0/\1=0)
4) ложное высказывание (0/\0=0)
Запишите логические функции, соответствующие данным сложным высказываниям (в задании использовались строки из стихов А. С. Пушкина):
1). Мне вас не жаль, года весны моей.
2). На холмах Грузии лежит ночная мгла;
Шумит Арагва предо мною…
3). Унынья моего ничто не мучит, не тревожит.
4). Мне не спится, не огня;
Всюду мрак и сон докучный.
Ответ:
1) F(A) = не А
2) F(A, В) = А и В
3) F(A, В) = не А и не В
4) F(A, В, C, D) = не А и не В и С и D
Представьте данное высказывание «Число 6 делится на 2, и число 6 делится на 3» в виде логической формулы.
Решение: Обозначим через А простое высказывание «Число 6 делится на 2» — истинное высказывание, через В — «Число 6 делится на 3»- истинное высказывание. Простые высказывания соединены связкой и (конъюнкция), очевидно логическая формула имеет вид А /\ В. Ее значение ((1/\1=1) — истина.
Даны два высказывания: А= <3+2=5>и B=<круг имеет форму прямоугольника>. Определите, чему равны составные высказывания:
Ответ:
1) 0
2) 1
Определите истинность составного высказывания: ( ¬ А /\ ¬ B) /\ (C \/ D), состоящего из простых высказываний:
Решение:
Сначала устанавливаем истинность простых высказываний: А = 1, В = 0, С = 1, D = 0.
Затем определим истинность составного высказывания, используя таблицы истинности логических операций: (ø1/\ø0) /\ (1\/ 0) = (0 /\1) /\ (1 \/ 0) = 0
Ответ: ( ¬ 1/\ ¬ 0) /\ (1\/ 0) = (0 /\1) /\ (1\/ 0) = 0 — составное высказывание ложно.
Определите истинность составного высказывания:
Решение
Замените простые высказывания логическими переменными и установите их истинность или ложность:
А: «2*2 = 4» — истинно (1),
В: «3*3 = 10 — ложно (0),
С: «2*2 = 5» — ложно (0),
D: «3*3 = 9» — истинно (1).
Замените также логические связки «и» и «или» операциями логического умножения и логического сложения. Тогда составное высказывание примет вид следующего логического выражения: (А /\ В) \/ (С /\ D).
Подставьте вместо логических переменных их логические значения и определите истинность составного высказывания, используя таблицы истинности логических функций:
(1/\ 0) \/ (0/\1) = 0 + 0= 0.
Ответ: составное высказывание ложно.
Таблица истинности логических выражений
Содержание:
Построение таблиц истинности для логических выражений
Для логического выражения можно построить таблицу истинности, показывающую, какие значения принимает выражение при всех наборах значений входящих в него переменных. Для построения таблицы истинности следует:
Построим таблицу истинности для логического выражения 
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Заполненная таблица истинности имеет вид:
Обратите внимание, что последний столбец (результат) совпал со столбцом А. В таком случае говорят, что логическое выражение 
Возможно вам будут полезны данные страницы:
Свойства логических операций
Рассмотрим основные свойства логических операций, называемые также законами алгебры логики.
1. Переместительный (коммутативный) закон:
• для логического умножения:
• для логического сложения:
2. Сочетательный (ассоциативный) закон:
• для логического умножения:
• для логического сложения:
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
3. Распределительный (дистрибутивный) закон:
• для логического умножения:
• для логического сложения:
4. Закон двойного отрицания:
Двойное отрицание исключает отрицание.
5. Закон исключённого третьего:
• для логического умножения:
• для логического сложения:
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
6. Закон повторения:
• для логического умножения:
• для логического сложения:
7. Законы операций с 0 и 1:
• для логического умножения:
• для логического сложения:
8. Законы общей инверсии:
• для логического умножения:
• для логического сложения:
Законы алгебры логики могут быть доказаны с помощью таблиц истинности
Докажем распределительный закон для логического сложения:
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
Примеры с решением
Пример 1.
Найдём значение логического выражения 
Решение:
При X = 0 получаем следующее логическое выражение: 
Для решения задач вам понадобится знание таблиц истинности логических операций:

Порядок выполнения логических операций задается круглыми скобками
Сначала выполняется операция отрицания НЕ
после И выполняется ИЛИ
и в последнюю очередь — эквивалентность.
Задача 1
Дан фрагмент таблицы истинности выражения F:

Решение:
Чтобы определить верное выражение, надо значения А,В,С каждой из строк таблицы подставить в очередное выражение, определить его результат выполнения и сравнить со значением F соответствующей строки.
То выражение, значения которого совпадут со значениями столбца F, и будет искомым. Решение:
Задача 2
Дан фрагмент таблицы истинности выражения F:

Решение:
1) В каждом из приведенных выражений логические переменные связывает только один тип логической операции. В 1 и 3 вариантах это операция И (

2) По столбцу F видно, что выражение для двух комбинаций данных истинно, а для одной — ложно. Следовательно, выражение не может быть логическим умножением (И), так как логическое умножение истинно только для одной комбинации данных, а в таблице две истины. Следовательно, искомое выражение является логическим сложением (ИЛИ) значений логических переменных.
Поэтому, в качестве ответа может быть 2 или 4 вариант. Рассмотрим их.
1) 2-й вариант: В первой строке таблицы истинности отображены только значения х1, хЗ, х5, и все они равны 0. Но в формуле 2го варианта у нас х5 отрицается, то есть значение х5 будет изменено на 1, и в результате всё выражение должно быть истинным. Что не соответствует заданной таблице. Остаётся 4-й вариант.
2) Как мы видим, переменные х1, хЗ и х5 в 4-м варианте ответа не отрицаются, что соответствует первой строке заданной таблицы.
Задача 4
Какое из приведенных имен сказочных героев удовлетворяет логическому условию:
Решение:
Составим для каждого из предложенных ответов схему соответственно заданной логической формуле. Ищем истинное значение.
И так с каждым вариантом ответа, пока не найдете истину.
Задача 5
Логическая функция F задаётся выражением
Определите, какому столбцу таблицы истинности функции F соответствует каждая из

Решение 1:
Последней операцией выполнения является операция 

Рассмотрим все случаи, когда F = 1 (это значения в строках 1 и 3):
— не рассматриваем, т.к. в табл, нет строки, где все значения логических переменных = 1.

Решение 2:
Последней операцией выполнения является операция 

Выражение F равно 1 в 1й и Зй строках, в этих же строках только “Перем.3”=1, следовательно, значение X находится в 3-м столбце.
Теперь рассмотрим построчно значения 1-х двух столбцов:
1 строка: 0 и О, Y = Z. Поэтому Y и Z для столбцов не определить.
2 строка: 0 и 1. Независимо будет ли Y=0 Z=1 или Y=1 Z=0, функция F=0 т.к. уже
Х=0. Поэтому Y и Z для столбцов не определить.
3 строка: 0 и 1. В этой строке функция F=1, значит 
невозможна, иначе F будет = 0. Комбинация 
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.
Что такое алгебра и алгебра логики
Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.
Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.
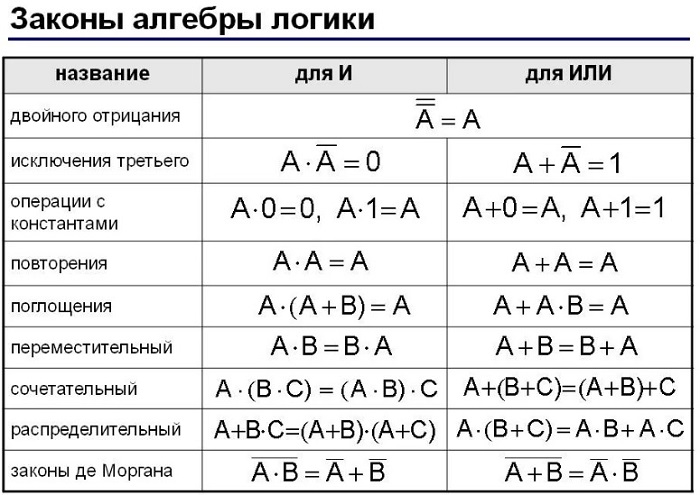
Законы алгебры логики
Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.
Основные законы алгебры логики представлены в таблице:
Логические выражения
В информатике предоставляется два вида высказываний: простое и сложное.
Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.
Нью-Йорк — столица США (ложное);
в России 1117 городов (верное).
Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.
Идёт дождь, а у меня нет зонта.
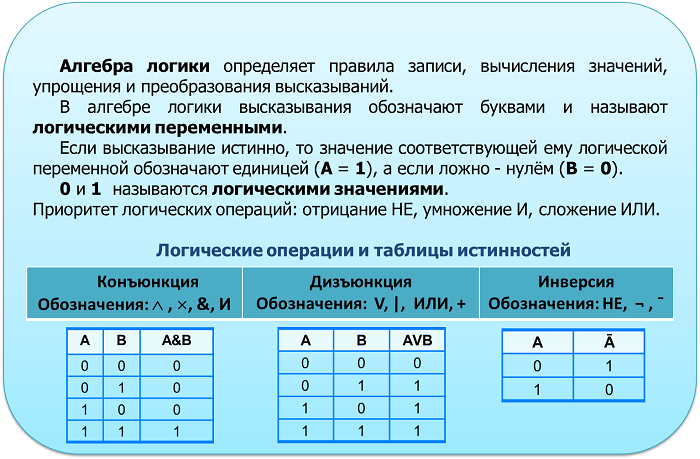
Основные логические операции
Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.
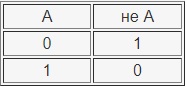
Логическое отрицание (инверсия) —НЕ
Таблица истинности инверсии:
Результаты операции НЕ следующие:
если исходное выражение истинно, то результат его отрицания будет ложным;
если исходное выражение ложно, то результат его отрицания будет истинным.
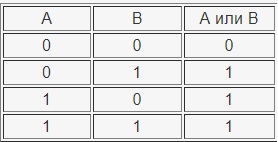
Логическое сложение (дизъюнкция, объединение) — ИЛИ
Понятие «Логическое ИЛИ» также можно заменить понятием «Дизъюнкция». Данная операция обозначается знаками — ИЛИ, OR, ||, |.
Но есть небольшое отличие: в «Логическом И» результат отрицания равен единице, если оба обозначения равны единице, а в «Логическом ИЛИ» итог равен единице, если одно из обозначений равно единице.
Таблица истинности операции ИЛИ:
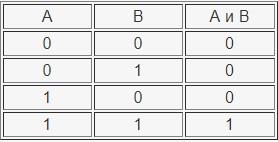
Логическое умножение(конъюнкция) — И
В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.
За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).
При всех остальных значениях операция будет ложной.
Таблица истинности операции И приведена ниже:
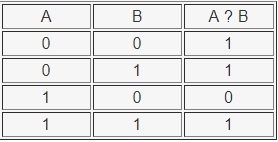
Логическое следование (импликация) — ЕСЛИ ТО
Данная программа имеет также название «Импликация». Она образуется из двух высказываний, которые соединяет: «если. то».
Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if. then.
Таблица истинности операции ЕСЛИ ТО выглядит так:
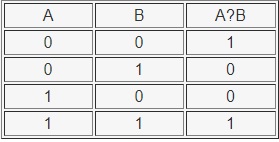
Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.
И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.
Таблица истинности операции эквивалентности:
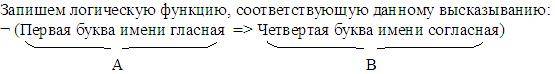

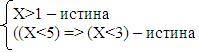


























 — не рассматриваем, т.к. в табл, нет строки, где все значения логических переменных = 1.
— не рассматриваем, т.к. в табл, нет строки, где все значения логических переменных = 1.