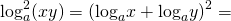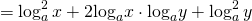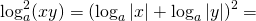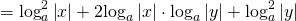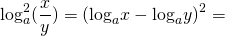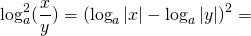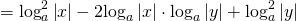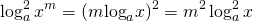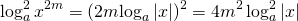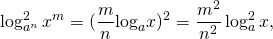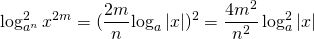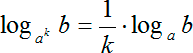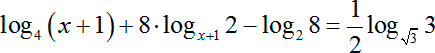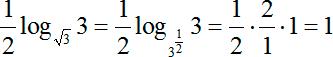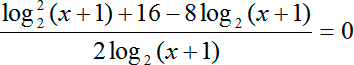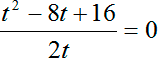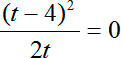Как решить квадратный логарифм
Как возвести логарифм в квадрат
Как возвести логарифм в квадрат, когда под знаком логарифма стоит произведение или частное? Как упростить квадрат логарифма степени?
Как возвести в квадрат логарифм произведения.
Так как логарифм произведения равен сумме логарифмов, квадрат логарифма произведения равен квадрату суммы логарифмов множителей:
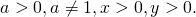
Если изменить условия:
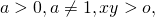
то каждый из множителей под знаком логарифма нужно брать по модулю:
Как возвести в квадрат логарифм частного.
Так как логарифм частного равен разности логарифмов, то квадрат логарифма частного равен квадрату разности логарифмов делимого и делителя:
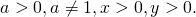
При изменении условий
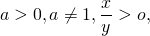
под знаком логарифма появляются модули:
Возведение в квадрат логарифма степени.
В логарифме степени показатель можно вынести за знак логарифма.
При возведении в квадрат логарифма степени показатель степени также следует возвести в квадрат:
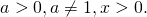
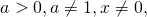
то при чётном показателе степени при вынесении показателя за знак логарифма под знаком логарифма появляется модуль:
Аналогично возводят в квадрат логарифм со степенью в основании:
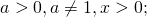
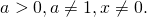
Уравнения, квадратные относительно логарифма, и прочие нестандартные приемы
На уравнениях такого вида многие ученики «зависают». При этом сами задачи отнюдь не являются сложными — достаточно просто выполнить грамотную замену переменной, для чего следует научиться выделять устойчивые выражения.
В дополнение к этому уроку вас ждет довольно объемная самостоятельная работа, состоящая из двух вариантов по 6 задач в каждом.
Метод группировки
Сегодня мы разберем два логарифмических уравнения, одно из которых не решается «напролом» и требует специальных преобразований, а второе. впрочем, не буду рассказывать все сразу. Смотрите видео, скачивайте самостоятельную работу — и учитесь решать сложные задачи.
Итак, группировка и вынесение общих множителей за скобку. Дополнительно я расскажу вам, какие подводные камни несет область определения логарифмов, и как небольшие замечания по области определений могут существенно менять как корни, так и все решение.
Начнем из группировки. Нам нужно решить следующее логарифмическое уравнение:
log2 x · log2 ( x − 3) + 1 = log2 ( x 2 − 3 x )
В первую очередь отметим, что x 2 − 3 x можно разложить на множители:
Затем вспоминаем замечательную формулу:
Сразу же небольшое замечание: данная формула прекрасно работает, когда а, f и g — обычные числа. Но когда вместо них стоят функции, данные выражения перестают быть равноправными. Представьте себе такую гипотетическую ситуацию:
f g fg будет положительным, следовательно, log a ( fg ) будет существовать, а вот log a f и log a g отдельно существовать не будут, и выполнить такое преобразование мы не сможем.
Игнорирование данного факта приведет к сужению области определения и, как следствие, к потере корней. Поэтому прежде чем выполнять такое преобразование, нужно обязательно заранее убедиться, что функции f и g положительные.
Следовательно, в функции log2 x ( x − 3) каждый множитель будет больше нуля. Поэтому можно смело раскладывать произведение на сумму:
log2 x log2 ( x − 3) + 1 − log2 x − log2 ( x − 3) = 0
На первый взгляд может показаться, что легче не стало. Напротив: количество слагаемых лишь увеличились! Чтобы понять, как действовать дальше, введем новые переменные:
А теперь сгруппируем третье слагаемое с первым:
( a · b − a ) + (1 − b ) = 0
a (1 · b − 1) + (1 − b ) = 0
Заметим, что и в первой, и во второй скобке стоит b − 1 (во втором случае придется вынести «минус» за скобку). Разложим нашу конструкцию на множители:
a (1 · b − 1) − ( b − 1) = 0
А теперь вспоминаем наше замечательно правило: произведение равно нулю, когда хотя бы один из множителей равен нулю:
Вспоминаем, что такое b и а. Получим два простейших логарифмических уравнения, в которых останется лишь избавиться от знаков logи приравнять аргументы:
Мы получили два корня, но это не решение исходного логарифмического уравнения, а лишь кандидаты в ответ. Теперь проверим область определения. Для первого аргумента:
Оба корня удовлетворяют первому требованию. Переходим ко второму аргументу:
А вот здесь уже x = 2 нас не удовлетворяет, зато x = 5 вполне нас устраивает. Следовательно, единственным ответом будет x = 5.
Переходим ко второму логарифмическому равнению. На первый взгляд, оно существенно проще. Однако в процессе его решения мы рассмотрим тонкие моменты, связанные с областью определения, незнание которых существенно усложняет жизнь начинающим ученикам.
log0,7 ( x 2 − 6 x + 2) = log0,7 (7 − 2 x )
Перед нами каноническая форма логарифмического уравнения. Ничего преобразовывать не нужно — даже основания одинаковые. Поэтому просто приравниваем аргументы:
x 2 − 6 x + 2 = 7 − 2 x
x 2 − 6 x + 2 − 7 + 2 x = 0
Перед нами приведенное квадратное уравнение, оно легко решается по формулам Виета:
Но эти корни еще не являются окончательными ответами. Нужно найти область определения, поскольку в исходном уравнении присутствуют два логарифма, т.е. учет области определения строго обязателен.
Итак, выпишем область определения. С одной стороны, аргумент первого логарифма должен быть больше нуля:
С другой — второй аргумент тоже должен быть больше нуля:
Эти требования должны выполняться одновременно. И вот тут начинается самое интересное. Безусловно, мы можем решить каждое из этих неравенств, затем пересечь их и найти область определения всего уравнения. Но зачем так усложнять себе жизнь?
Давайте заметим одну тонкость. Избавляясь от знаков log, мы приравниваем аргументы. Отсюда следует, что требования x 2 − 6 x + 2 > 0 и 7 − 2 x > 0 равносильны. Как следствие, любое из двух неравенств можно вычеркнуть. Давайте вычеркнем самое сложное, а себе оставим обычное линейное неравенство:
x x = −1, потому что x = 5 > 3,5.
Можно записать ответ: x = 1 является единственным решением исходного логарифмического уравнения.
Выводы из данного логарифмического уравнения следующие:
Вот, собственно, и все, что я хотел рассказать о группировке.:)
Типичные ошибки при решении
Сегодня мы разберем два типичных логарифмических уравнения, на которых спотыкаются многие ученики. На примере этих уравнения мы увидим, какие ошибки чаще всего допускаются в процессе решения и преобразования исходных выражений.
Дробно-рациональные уравнения с логарифмами
Сразу следует отметить, что это довольно коварный тип уравнений, в которых отнюдь не всегда сразу присутствует дробь с логарифмом где-то в знаменателе. Однако в процессе преобразований такая дробь обязательно возникнет.
При этом будьте внимательны: в процессе преобразований изначальная область определения логарифмов может существенно измениться!
Переходим к еще более жестким логарифмическим уравнениям, содержащим дроби и переменные основания. Чтобы за один короткий урок успеть больше, я не буду рассказывать элементарную теорию. Сразу перейдем к задачам:
4 log25 ( x − 1) − log3 27 + 2 log x − 1 5 = 1
Посмотрев на это уравнение, кто-то спросит: «При чем здесь дробно-рациональное уравнение? Где в этом уравнении дробь?» Давайте не будем спешить и внимательно посмотрим на каждое слагаемое.
Итак, второе слагаемое — это просто тройка. Третье слагаемое: 2 log x − 1 5. Тут тоже не все просто: в основании стоит функция, в аргументе — обычное число. Предлагаю перевернуть весь логарифм по следующей формуле:
Такое преобразование можно выполнить только если b ≠ 1. Иначе логарифм, который получится в знаменателе второй дроби, просто не будет существовать. В нашем случае b = 5, поэтому все в порядке:
2 log x − 1 5 = 2/log5 ( x − 1)
Перепишем исходное уравнение с учетом полученных преобразований:
4 log25 ( x − 1) − 3 + 2/ log5 ( x − 1) = 1
Другими словами, степень в основании логарифма становится дробью спереди. А выражение перепишется так:
4 1/2 log5 ( x − 1) − 3 + 2/ log5 ( x − 1) − 1 = 0
У нас получилось длинное уравнение с кучей одинаковых логарифмов. Введем новую переменную:
А вот это уже дробно-рациональное уравнение, которое решается средствами алгебры 8—9 класса. Для начала разделим все на двойку:
В скобках стоит точный квадрат. Свернем его:
Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля. Никогда не забывайте про этот факт:
Вспоминаем, что такое t :
Избавляемся от знаков log, приравниваем их аргументы, и получаем:
С другой стороны, тот же x − 1 присутствует и в основании, поэтому должен отличаться от единицы:
Эти требования должны выполняться одновременно. Значение x = 6 удовлетворяет обоим требованиям, поэтому является x = 6 окончательным решением логарифмического уравнения.
Переходим ко второй задаче:
Вновь не будем спешить и посмотрим на каждое слагаемое:
log4 ( x + 1) — в основании стоит четверка. Обычное число, и его можно не трогать. Но в прошлый раз мы наткнулись на точный квадрат в основании, который пришлось выносить из-под знака логарифма. Давайте сейчас сделаем то же самое:
8 log x + 1 2 = 8 · (1/log2 ( x + 1)) = 8/log2 ( x + 1)
Следующее слагаемое — log2 8. Это константа, поскольку и аргументе, и в основании стоят обычные числа. Найдем значение:
То же самое мы можем сделать и с последним логарифмом:
Теперь перепишем исходное уравнение:
1/2 · log2 ( x + 1) + 8/log2 ( x + 1) − 3 − 1 = 0;
log2 ( x + 1)/2 + 8/log2 ( x + 1) − 4 = 0
Приведем все к общему знаменателю:
Перед нами опять дробно-рациональное уравнение. Введем новую переменную:
Перепишем уравнение с учетом новой переменной:
Будьте внимательны: на этом шаге я поменял слагаемые местами. В числителе дроби стоит квадрат разности:
Как и в прошлый раз, дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля:
Получили один корень, который удовлетворяет всем требованиям, поэтому возвращаемся к переменной x :
Все, мы решили уравнение. Но поскольку в исходном уравнении присутствовало несколько логарифмов, необходимо выписать область определения.
Так, выражение x + 1 стоит в аргументе логарифма. Поэтому x + 1 > 0. С другой стороны, x + 1 присутствует и в основании, т.е. x + 1 ≠ 1. Итого:
Удовлетворяет ли найденный корень данным требованиям? Безусловно. Следовательно, x = 15 является решением исходного логарифмического уравнения.
Вот и все, о чем я хотел сегодня рассказать. Надеюсь, этот урок поможет вам в решении сложных логарифмических уравнений. Смотрите другие видеоуроки, скачивайте и решайте самостоятельные работы, и до встречи в следующем видео!
Определение логарифма, его свойства и график
Логарифм числа – это показатель степени, в которую нужно возвести одно число, чтобы получить другое.
Если число b в степени y равняется x:
Значит логарифм числа x по основанию b равен y:
Например:
Логарифм как обратная функция к показательной
Натуральный логарифм (ln)
Натуральный логарифм – это логарифм по основанию е.
Число e – это константа, которая может определяться как предел:
Обратный логарифм
Обратный логарифм (или антилогарифм) числа n – это число, логарифм которого по основанию a равен числу n.
Таблица свойств логарифмов
Ниже представлены основные свойства логарифмов в табличном виде.
| Свойство | Формула | Пример |
| Основное логарифмическое тождество | ||
| Логарифм произведения | ||
| Логарифм деления/частного | ||
| Логарифм степени | ||
| Логарифм числа по основанию в степени | » data-order=» «> «>  | » data-order=» «> «>  |
| Логарифм корня | » data-order=» «> «>  | » data-order=» «> «>  |
| Перестановка основания логарифма | ||
| Переход к новому основанию | ||
| Производная логарифма | ||
| Интеграл логарифма | ||
| Логарифм отрицательного числа | ||
| Логарифм числа, равного основанию | ||
| Логарифм бесконечности |
Логарифмическая функция
Функция, которая определена формулой f(x)=loga(x) – это логарифмическая функция с основанием a. При этом a>0, a≠1.
График функции логарифма
График логарифмической функции (логарифмика) может быть двух типов, в зависимости от значения основания a:
Свойства логарифмов и примеры их решений
Зачем в жизни нужны логарифмы?
Я уже говорил, что математики СУПЕРленивые люди? Это правда.
Вот представь себе, им лень умножать и они придумали логарифмы, которые позволяют заменить умножение сложением!
Им еще больше лень возводить в степень и они используют логарифмы, чтобы заменить возведение в степень умножением или делением!
То есть они используют логарифмы, чтобы быстро проделывать громоздкие вычисления.
Логарифм и его свойства. Вебинар (1 час 48 минут)
В этом видео мы разобрали свойства логарифмов на примере решения 35 задач.
Начиная от самых простых логарифмов и заканчивая сложными.
Если вам понравилось видео, подписывайтесь на канал, ставьте лайки — нам будет приятно и мы будем делать такие видео впредь.
Что такое логарифм?
Для начинающих объясним все человеческим языком. Логарифмы – очень простая тема.
Чтобы понять, как их решать, нужно всего лишь разобраться, что как называется, знать таблицу умножения и уметь возводить в число в степень.
Все. Больше ничего не нужно.
Начнем с простого. Как решить уравнение \(\displaystyle <<2>^
Очень легко – просто ответь на вопрос в какую степень нужно возвести число \(2\) чтобы получить \(8\)?
Решаем методом подбора: два в первой степени – нет, два во второй степени – нет, два в третей степени – ДА!
Двойку нужно возвести в ТРЕТЬЮ степень, чтобы получить восемь (\(\displaystyle <<2>^<3>>=8\)) и значит решением уравнения будет число три (\(x=3\)).
Следующий вопрос. Как решить уравнение \(\displaystyle <<2>^
Опять просто ответь на вопрос в какую степень нужно возвести число \(2\), чтобы получить число \(5\)?
Попытаемся подобрать: два во второй степени равно четыре – мало, два в третьей степени равно восемь – много.
Метод подбора сразу ответ не дает… Да и вообще, в этом случае подобрать решение не получится – ведь это не только нецелое число, это число даже не рациональное.
Для нахождения таких решений было придумано понятие логарифм:
В общем виде он записывается так:
То есть логарифм – это степень, в которую нужно возвести основание, чтобы получить аргумент.
Если ты посчитаешь на калькуляторе, то получишь \(2,321928\ldots \) и т.д. Это число иррациональное. Оно мало того, что не подбирается, оно еще и не кончается…
Ну и как с такими числами работать? Как их запоминать? Как их записывать?
В нашем случае решение уравнения можно записать как \(2,321928\ldots \) или как \(\displaystyle <<\log >_<2>>5\).
Согласись второе выражение гораздо удобнее, чем первое. И оно, кстати, абсолютно точное. Словами это произносится как:
Решением уравнения два в степени икс равно пяти является логарифм пяти по основанию два, или логарифм по основанию два от пяти.
Кстати, а ты заметил что и у степени числа и у логарифма основание всегда находится «ВНИЗУ». Легко запомнить правда? А вот «вверху», у степени находится ее показатель, а у логарифма – аргумент.
Выражение \(\displaystyle <<2>^<3>>=8\) можно также записать в виде \(\displaystyle <<\log >_<2>>8=3\). Читается так:
«Логарифм восьми по основанию два равен трем»
«Логарифм по основанию два от восьми равен трем»
Теперь более общая запись:
«Чтобы получить число \(b\), нужно число \(a\) возвести в степень \(c\)»:
8 примеров вычисления логарифмов
Пример 1
Чему равен \(\displaystyle <<\log >_<2>>4\)?
\(\displaystyle <<\log >_<2>>4=2\), так как число \(2\) нужно возвести во вторую степень, чтобы получить \(4\).
Пример 2
Чему равен \(\displaystyle <<\log >_<2>>\frac<1><8>\)?
Заметим, что \(\displaystyle 8=<<2>^<3>>\), тогда \(\displaystyle \frac<1><8>=\frac<1><<<2>^<3>>>=<<2>^<-3>>\), то есть \(2\) нужно возвести в степень \(-3\), чтобы получить \(\displaystyle \frac<1><8>\).
Пример 3
А чему равен \(\displaystyle <<\log >_<2>>0,25\)?
Обращать внимание нужно, в первую очередь, на основание. Возможно ли представить \(0,25\) как \(2\) в какой-то степени? Да, возможно: запишем это число в виде обычной дроби: \(\displaystyle 0,25=\frac<1><4>=\frac<1><<<2>^<2>>>=<<2>^<-2>>\).
Пример 4
Чему равен \(\displaystyle <<\log >_<7>>1\)?
В какую степень надо возвести \(7\), чтобы получить \(1\)? Вспоминаем, что любое число в нулевой степени равно \(1\) (подробнее читай в разделе «Степень и ее свойства»).
Значит, \(\displaystyle <<\log >_<7>>1=0\). Более того, логарифм с любым основанием от единицы равен \(0\).
Пример 5
\(\displaystyle <<\log >_<4>>2\). В этом случае аргумент \(2\) равен корню основания: \(\displaystyle 2=\sqrt<4>\).
Но мы помним, что корень тоже можно представить в виде степени (с дробным показателем): \(\displaystyle 2=\sqrt<4>=<<4>^<\frac<1><2>>>\text< >\Rightarrow \text< ><<\log >_<4>>2=\frac<1><2>\).
Попробуй найти следующие 4 логарифма самостоятельно
Десятичные логарифмы
Логарифм по основанию \(\displaystyle 10\) называется десятичным логарифмом и записывается упрощенно: \(\displaystyle \lg \) вместо \(\displaystyle <<\log >_<10>>\)
Когда нужная степень не подбирается
Как я уже говорил, далеко не всегда удается подобрать такую степень. Но это не значит, что такого числа не существует, просто его можно вычислить только на калькуляторе.
Например, \(\displaystyle <<\log >_<2>>5=2,321928…\).
Видим, что это число расположено между \(\displaystyle 2\) и \(\displaystyle 3\), и это понятно: ведь это значит, чтобы получить \(5\), нужно \(2\) возводить в степень больше \(2\), но меньше \(3\).
На ЕГЭ пользоваться калькулятором нельзя, но даже если бы было можно, нельзя записывать приближенные вычисления.
Поэтому, если перед нами задача первой части, ответ обязательно должен получиться «хороший», и его можно посчитать в уме.
В письменной части могут попасться и «плохие» числа; в этом случае пугаться не нужно, в ответе можно просто написать логарифм.
Например, ответ вполне может выглядеть так:
\(\displaystyle <<\log >_<3>>10\), или даже так: \(\displaystyle \frac<2+<<\log >_<3>>7><5>\).
Получается, что теперь мы можем мгновенно записать решение любого элементарного показательного уравнения:
Но увлекаться и халтурить тоже не стоит – если в ответе оставить \(\displaystyle x=<<\log >_<3>>81\), высший балл за задачу не поставят.
То есть, если ответ возможно упростить и представить в виде рационального числа, это обязательно нужно будет сделать.
Потренируйся на следующих простых примерах:
6 примеров для самостоятельной работы
Ответы:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Область допустимых значений (ОДЗ)логарифма
Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:
То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться \( 1\).
Начнем с простого: допустим, что \( a=1\). Тогда, например, число не существует, так как в какую бы степень мы не возводили \( 1\), всегда получается \( 1\).
Более того, \( \displaystyle <<\log >_<1>>b\) не существует ни для какого \( \displaystyle b\ne 1\).
Но при этом \( \displaystyle <<\log >_<1>>1\) может равняться чему угодно (по той же причине – \( 1\) в любой степени равно \( 1\)).
Поэтому объект не представляет никакого интереса, и его просто выбросили из математики.
Похожая проблема у нас и в случае \( a=0\): \( 0\) в любой положительной степени – это \( 0\), а в отрицательную его вообще нельзя возводить, так как получится деление на ноль (напомню, что \( \displaystyle <^<-c>>=\frac<1><<^
При \( a 0\\x\ne 1\\x+2>0\end
Пример 1 (попробуй решить самостоятельно)
Найдите корень уравнения \( \displaystyle <<\log >_
Решение:
\( \displaystyle <<\log >_
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Основное логарифмическое тождество
Вспомним определение логарифма в общем виде:
Подставим во второе равенство вместо \( \displaystyle c\) логарифм:
Это равенство называется основным логарифмическим тождеством. Хотя по сути это равенство – просто по-другому записанное определение логарифма:
Реши еще следующие примеры:
Пример 2
Найдите значение выражения \( \displaystyle <<25>^<<<\log >_<5>>3>>\).
Пример 3
Решения примеров 2 и 3:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Свойства логарифмов
К сожалению, задачи не всегда такие простые – зачастую сперва нужно упростить выражение, привести его к привычному виду, и только потом будет возможно посчитать значение.
Это проще всего сделать, зная свойства логарифмов.
Так что давай выучим основные свойства логарифмов. Каждое из них я буду доказывать, ведь любое правило проще запомнить, если знать, откуда оно берется.
Все эти свойства нужно обязательно запомнить, без них большинство задач с логарифмами решить не получится.
А теперь обо всех свойствах логарифмов подробнее.
Свойство 1 – степень аргумента
Доказательство:
Свойство 2 – сумма логарифмов
Сумма логарифмов с одинаковыми основаниями равна логарифму произведения: \( \displaystyle <<\log >_>b+<<\log >_>c=<<\log >_>\left( b\cdot c \right)\).
Доказательство:
Пример
Найдите значение выражения: \( \displaystyle <<\log >_<3>>5+<<\log >_<3>>0,6\).
Решение:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
А вот обещанное упрощение:
Зачем это нужно? Ну например: чему равно \( \displaystyle lo<
Теперь упрости сам:
Ответы:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Свойство 3 – разность логарифмов
| Разность логарифмов с одинаковыми основаниями равна логарифму частного:\( \displaystyle lo< |
Доказательство:
Все точно так же, как и в пункте 2:
Пример из прошлого пункта теперь становится еще проще:
Пример посложнее: \( \displaystyle \log _<2>^<2>2\sqrt<3>-\log _<2>^<2>\sqrt<3>—<<\log >_<2>>3\).
Догадаешься сам, как решить?
Здесь нужно заметить, что у нас нету ни одной формулы про логарифмы в квадрате. Это что-то сродни выражению \( \displaystyle <<2>^<<
Поэтому отвлечемся от формул про логарифмы, и подумаем, какие вообще формулы мы используем в математике чаще всего? Еще начиная с 7 класса!
Это – формулы сокращенного умножения. Нужно привыкнуть к тому, что они везде! И в показательных, и в тригонометрических, и в иррациональных задачах они встречаются. Поэтому их нужно обязательно помнить.
Нажми на ссылку «Формулы сокращенного умножения», и внимательно на них посмотри. Какую из них можно применить здесь?
Если присмотреться к первым двум слагаемым, становится ясно, что это разность квадратов:
Дальше все просто – применяем только что выученные правила 2 и 3. Что получилось?
Ответ для проверки:
Упрости сам:
Ответы:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Свойство 4 – вынесение показателя степени из аргумента логарифма
Если в аргументе логарифма стоит степень, показатель этой степени можно вынести за знак логарифма: \( \displaystyle <<\log >_><^
>=n\cdot <<\log >_>b\)
Доказательство:
Можно понять это правило так:
То есть степень аргумента выносится вперед логарифма, как коэффициент.
Пример: Найдите значение выражения \( \displaystyle \frac<<<\log >_<2>>25><<<\log >_<2>>5>\).
Реши сам:
Ответы:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Свойство 5 – вынесение показателя степени из основания логарифма
Доказательство:
Запоминаем: из основания степень выносится как обратное число, в отличии от предыдущего случая!
Свойство 6 – вынесение показателя степени из основания и аргумента логарифма
Если в основании и аргументе логарифма стоят степени, показатели этих степеней можно вынести за знак логарифма: \( \displaystyle <<\log >_<<^
>>><^ >=\frac \cdot <<\log >_>b\).
Свойство 7 – переход к новому основанию
Если основания логарифмов разные, то для того чтобы дальше работать с логарифмами нужно перейти к логарифмам с одним основанием: \( \displaystyle <<\log >_>b=\frac<<<\log >_
>b><<<\log >_ >a>\text< >\left( c>0;\text< >\ne \text <1>\right)\).
Доказательство:
Свойство 8 – замена местами основания и аргумента логарифма
Можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе: \( \displaystyle <<\log >_>b=\frac<1><<<\log >_>a>,\text< >\left( b\ne 1 \right)\).
Доказательство:
Рассмотрим еще несколько примеров.
Пример 1. Найдите значение выражения \( \displaystyle <<\log >_<5>>75+<<\log >_<5>>\frac<1><3>\).
Пример 2. Найдите значение выражения \( \displaystyle <<\log >_<3>>36-2<<\log >_<3>>2\).
Пример 3. Найдите значение выражения \( \displaystyle <<\log >_<8\sqrt[5]<4>>>\left( 32\sqrt[5] <2>\right)\).
Пример 4. Найдите значение выражения \( \displaystyle \frac<\log _<5>^<2>25\sqrt<10>-\log _<5>^<2>\sqrt<10>><<<\log >_<5>>250>.\).
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Наши курсы по подготовке к ЕГЭ по математике, информатике и физике
Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.
Твой ход!
Теперь ты знаешь о логарифмах все! Самое время покорять уравнения и неравенства!
Я уверен, что ты справишься. И я очень тобой горжусь. Ведь ты решил сесть и разобраться.
Напиши нам в комментариях ниже, что думаешь об этой статье. Все ли было понятно? Понравилась ли она тебе?
А еще ты можешь задать нам любой вопрос. И мы обязательно ответим!
Добавить комментарий Отменить ответ
20 комментариев
Отличный материал! Спасибо!
Спасибо, Саид. В каком вы классе?
Вы — это просто чу-до, и этот учебник тоже! Если бы я знала о вас в сентябре, я бы выбрала вашу онлайн школу
Спасибо большое, Бася! Очень приятно слышать. Желаем вам сдать ЕГЭ на 100 баллов! )
Как лайк поставить?
Будем считать этот коммент лайком. Спасибо!
хотела зарегистрироваться на вебинар 14 февраля, но не смогла: «сайт не может обеспечить безопасное соединение» может есть еще вариант?
Надежда, я зарегистрировал вас и отправил на почту доступы. Скажите, пожалуйста, где вы столкнулись с такой надписью? Можете написать или отправить ссылку?
Большое спасибо, все изложено четко и красиво!
Инна, очень рады, что понравилось! Заходите к нам еще! )
Это лучшее объяснение, что я встречала! Хорошая методика: простой язык, примеры и практика! Я благодарна Клеверу!
Спасибо, Ника! И за название тоже. «Клевер» — клёво! ))
Некоторые комментарии прошлых лет к этой статье:
Катерина
10 января 2018
Я получила очень хорошую для меня информацию.
Александр (Админ)
11 января 2018
Спасибо, Катерина. Нам очень приятно слышать, что наш учебник полезен.
Владимир
17 января 2018
Прекрасное объяснение! Просто великолепное! В примере после третьего свойства действительно есть опечатка. знак корня у третьего члена лишний. Есть также потерянный член в конце предпоследней строчки решения пятой задачи третьего свойства. В финальной строчке он нашелся 🙂
Алексей Шевчук
06 февраля 2018
Александр, примени свойство степени «произведение степеней с одинаковым основанием»: https://youclever.org/book/stepen-i-ee-svojstva
Дарья
10 декабря 2018
А как решать функцию логарифмическую, если логарифм под знаком модуля? Например y=[lgx]-lgx?
Шура
24 января 2019
Как сложить логарифмы если у обоих аргумент x, но у первого основание 2, а у второго 3?
Алексей Шевчук
04 февраля 2019
Шура, нужно воспользоваться формулой перехода к другому основанию Например, log_3 (x) = log_2 (x) / log_2 (3).
Олег
14 апреля 2019
Большое спасибо за очередную великолепную статью, все понятно.
Александр (админ)
14 апреля 2019
Олег, очень рады слышать! Удачи!
Олег
17 апреля 2019
Спасибо за статью, но СЛОЖНА
Александр (админ)
17 апреля 2019
Пожалуйста, Олег. Ну что поделать? Тяжело в ученье, легко на ЕГЭ )
Саня
06 сентября 2019
А что делать, если логарифмы с разными приколами? 0-0 Как их решать?
Алексей Шевчук
06 сентября 2019
Саня, посмотри статью про логарифмические уравнения, там некоторые приколы разобраны. https://youclever.org/book/logarifmicheskie-uravneniya-1
Алексей Шевчук
08 ноября 2019
Виталий, дело в том, что такие уравнения будут иметь действительные решения очень редко. Представим себе, что это уравнение (-2)^6x=-8. Тогда с одной стороны, x=0.5 является решением, но с другой стороны, когда мы решаем уравнение, у нас должна быть возможность воспользоваться свойствами степени: (-2)^6x = ((-2)^x)^6 — а теперь посмотрим, можем ли мы так делать? Подставим вместо x число 0.5: ((-2)^0.5)^6=-8. Вспомним, что такое степень 0.5? Это квадратный корень из числа. Но ведь мы не можем извлекать корень из отрицательного числа! Чтобы не возникало таких неприятностей, математики договорились не использовать отрицательные основания у показательной функции, а как следствие, и у логарифма. Но это касается только вычислений в действительных числах. Если мы рассматриваем также комплексные числа (это в которых можно извлекать корень из отрицательных чисел), то отрицательные основания возможны — но это уже не школьная математика.
Александр (админ)
08 ноября 2019
Отличное объяснение, Алексей! Снова вышли за пределы школьной математики. Это здорово! )
Виталий
12 ноября 2019
Спасибо за ответ. Понял, что это для облегчения начальной стадия обучения, с последующим переходом к более сложным вычислениям.
Антон
16 декабря 2019
Классное объяснение, спасибо!
Александр (админ)
16 декабря 2019
Антон, спасибо! Мы рады, что понравилось. Заходи еще! )
Света
07 января 2020
Спасибо очень понравилась то что не было не понятно все поняла
Александр (админ)
07 января 2020
Отлично, Света! Мы очень рады. Удачи тебе на экзаменах!
Александр (админ)
13 января 2020
То, что не нравится Полине Магаррамовой я переживу как-нибудь. Мне главное, чтобы вам нравилось 🙂
Евгений Вячеславович
06 февраля 2020
Классно… Если бы мне 19 лет назад так объясняли бы математику, я бы к егэ вообще не готовился бы, потому что все бы помнил и понимал. Так доходчиво и понятно я не встречал нигде. Спасибо вам.
Александр (админ)
06 февраля 2020
Спасибо, Евгений Вячеславович. Я вот тоже самое думаю, что, если бы мне объясняли также как здесь в свое время…. ))
Юлия Владимировна
13 мая 2020
Помогите решить: 2*log 1/2 (4x-5) — log1/2 *16x = log1/2(x-3)
Алексей Шевчук
14 мая 2020
Юлия Владимировна, двойку вносим в логарифм как степень аргумента: 2*log 1/2 (4x-5)=log 1/2 (4x-5)^2. Потом соединяем логарифмы по правилу вычитания: log 1/2 [(4x-5)^2 / 16x] = log1/2(x-3). Теперь можно от логарифмов избавиться: (4x-5)^2 /16x = (x-3) — получили обычное уравнение
Жахиян
27 мая 2020
В какую степень нужно возвести число 2 чтобы получить 8? как ответ может быть 3. По идей ответ дожен быть равно на 4 а не к 3.
Александр (админ)
27 мая 2020
Жахиян, вы говорите на какое число нужно УМНОЖИТЬ 2, чтобы получить 8. Это действительно 4. Но вопрос был В КАКУЮ СТЕПЕНЬ нужно возвести 2 чтобы получить 8. А это тройка: «два в третьей степени будет восемь» (2*2*2=8)
ООО,спасибо за последние слова,лучший сайт.