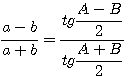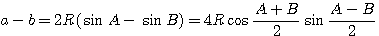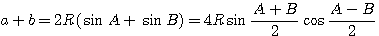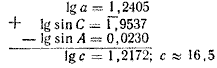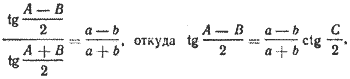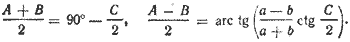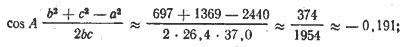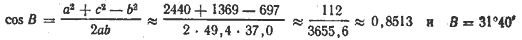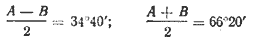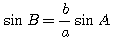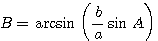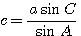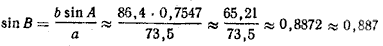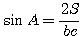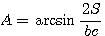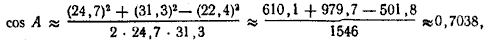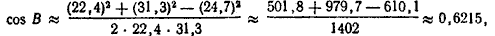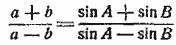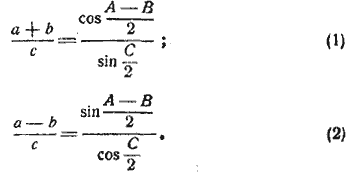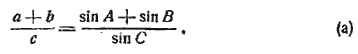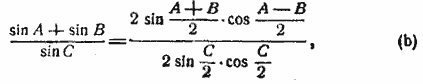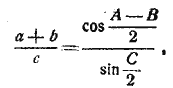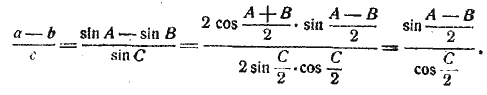Как решить косоугольный треугольник
Как решить косоугольный треугольник
Г л а в а П. Решение косоугольных треугольников
§7(41). Теорема тангенсов
Теорема. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов:
(и две аналогичные формулы для прочих пар сторон а, с и b, с).
Доказательство. В силу теоремы синусов имеем:
Разделив почленно эти равенства, получим доказываемую формулу.
§8(42). Решение треугольника по двум его углам и стороне
Задача. Даны два угла треугольника и сторона, прилежащая к ним; вычислить другие стороны и угол.
Даны В, С и а; требуется найти b, с и А.
Решение. Условие возможности построения треугольника по этим данным:
А + В 1 /0,9483 ≈ 1,055.
Вычисления выполнены по правилам приближённых вычислений. Значения синусов взяты из таблиц Брадиса; во всех промежуточных результатах сохраняются четыре значащие цифры (правило запасной цифры), а окончательный результат округлён до трёх значащих цифр.
Решение при помощи логарифмических таблиц. Имеем:
b = a sin B /sin A, lg b = lg a + lg sin В — lg sin A.
По таблицам найдем:
По таблицам Брадиса найдём b = 12,86. Однако в ответе следует оставить три значащие цифры, так как значение а дано с тремя значащими цифрами; поэтому b ≈ 12,9.
Сторона с вычисляется аналогично:
c = a sin C /sin A, lg c = lg a + lg sin C — lg sin A.
§9(43). Решение треугольника по двум сторонам и углу между ними
Задача. Даны две стороны треугольника и угол между ними; вычислить третью сторону и два других угла.
Пусть, например, даны а, b и С, требуется вычислить А, В и с.
Решение при помощи натуральных таблиц. Формула косинусов даёт выражение стороны с непосредственно через известные элементы:
с = \ / а 2 + b 2 — 2ab cos С
Для вычисления А можно также воспользоваться формулой косинусов:
Разность углов A — В можно вычислить, воспользовавшись теоремой тангенсов:
Углы А и В определяются из системы уравнений:
Сторону с можно вычислить по теореме синусов:
Пример. Дано: а ≈ 49,4; b ≈ 26,4; С ≈ 47°20′; найти А, В и с.
Решение при помощи натуральных таблиц. Имеем:
с 2 = а 2 + b 2 — 2ab cos С ≈ 49,4 2 + 26,4 2 — 2 • 49,4 • 26,4 • cos 47°20′
По таблицам квадратов найдём:
а 2 ≈ (49,4) 2 ≈ 2449; b 2 ≈ (26,4) 2 ≈ 697,0
2 • 49,4 • 26,4 • cos 47°20′ ≈ 2 • 49,4 • 2,64 • 0,6778 ≈ 1768.
Следовательно, с 2 ≈ 2440 + 697 — 1768 ≈ 1369. По таблицам квадратных корней
с ≈ 37,0. Далее
А ≈ arc cos (—0,191); угол А — тупой.
Находим дополнительный угол
180° — А ≈ arc cos (0,091) ≈ 79°; А ≈ 180° — 79° = 101°
(с округлением до 10′). Наконец,
Решение при помощи логарифмических таблиц. Вычислим углы A и В.
Из системы уравнений
найдём: A ≈ 101°, В ≈ 31°40′.
§ 10 (44). Решение треугольника по двум сторонам и углу,
противолежащему одной из них
Задача. Даны две стороны треугольника и угол А, лежащей против одной из них; вычислить третью сторону и два остальных угла.
Пусть даны a, b и А; требуется вычислить B, С и с
С л у ч а й 1. а > b, т. е, заданный угол А лежит против большей стороны.
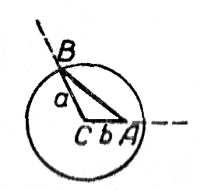
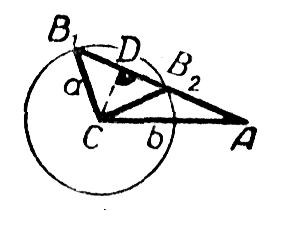
Построение показано на чертеже. Из точки С (как из центра), взятой на одной из сторон угла А на расстоянии b от вершины, описана окружность радиуса а; точка В есть точка пересечения этой окружности с другой стороной угла А.
Построение всегда возможно, задача имеет единственное решение.
Острый угол В, противолежащий меньшей стороне, находится по теореме синусов:
откуда
и затем С = 180° — (A + В). Сторона с находится по теореме синусов:
Значения угла В вычисляются по теореме синусов:
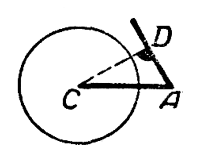
Из чертежа b) видно, что при
CD = b sin А > а окружность не пересечёт другой стороны угла А; задача не имеет решений.
В этом случае 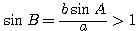
При CD = b sin А задача имеет единственное решение: треугольник ABC прямоугольный.
Случай 3. а = b. В этом случае треугольник ABC равнобедренный. Такой треугольник можно решить, разбразбив его высотой CD на два прямоугольных треугольника:
В = А; С = 180° — 2А; с = 2AD = 2а cos A.
Пример. Вычислить стороны и углы треугольника, если дано:
(деление на 73,5 можно заменить умножением на 1 /73,5 ≈ 0,0136, табл. 11).
Так как в данном случае а b sin A /a а + b, то треугольник с данными сторонами не существует. Будем считать, что с 2 =b 2 + с 2 — 2bc cos А
b 2 =c 2 + a 2 — 2ca cos B, откуда
Имеем далее: S = 1 /2 bc sin A. откуда
Угол А острый, так как он лежит против меньшей стороны; следовательно,
Точно также 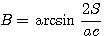
Итак, при решении треугольника по трём сторонам при помощи логарифмических таблиц углы, лежащие против меньших сторон, находятся по формулам, а угол, лежащий против наибольшей стороны, вычисляется как разность между 180е и суммой двух найденных углов.
Пример. Решить треугольник, зная длины (приближенные) его сторон: 24,7; 22,4 и 31,3. Обозначим a ≈ 22,4; b ≈ 24,7; с ≈ 31,3.
Решение при помощи натуральных таблиц. Имеем:
откуда А ≈ 45°20′ (с округлением до 10′).
откуда В ≈ 51°30′ и, наконец, С ≈ 180° — (45°20′ + 51°30′) ≈ 83°10′.
Решение при помощи логарифмических таблиц. Имеем:
sin А = 2S /bc, lg sin А = lg 2S — lg b — lg c.
Решить косоугольные треугольники по заданным основным элементам. (Решение каждого примера следует выполнить при помощи таблиц логарифмов и логарифмической линейки.)
81 (347). Даны сторона и два угла:
1) а ≈ 370,0; В ≈ 86°30′; С ≈ 50°50′
2) а ≈ 450,0; А ≈ 87°50′; В ≈ 10°50′.
3) а ≈ 951; B ≈ 126°40′; С ≈ 13°20′.
4) b ≈ 13,02; A ≈ 11°46′; B ≈ 133°40′.
82 (348). Даны две стороны и угол между ними:
1) а ≈ 510; b ≈ 317; С ≈ 76°10′.
2) а ≈ 225; b ≈ 800; С ≈ 36°40′.
3) а ≈ 2,296; с ≈ 1,687; В ≈ 29°52′.
4) b ≈ 28; c ≈ 42; А ≈ 124°.
83 (349). Даны две стороны и угол против одной из них:
2) b ≈ 360; с ≈ 309; С ≈ 21°30′.
3) а ≈ 13,89; с ≈ 8,42; А ≈ 126°41′.
4) а ≈ 13,81; с ≈ 8,14; С ≈ 14°37′.
5) b ≈ 263,1; с ≈ 215,4; В ≈ 70°14′.
6) а ≈ 19,06; b ≈ 88,19; А ≈ 31°17′.
84 (350). Даны три стороны:
85 (351). Решить косоугольные треугольники по заданным моментам:
1) R ≈ 7,92; А ≈ 113°17′; В ≈ 48°16′.
2) S ≈ 501,9; А ≈ 15°28′; B ≈ 45°23′.
5) а + b ≈ 488,8; А ≈ 70°24′; В ≈ 40°16′.
Как решить косоугольный треугольник
РЕШЕНИЕ КОСОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
При решении прямоугольных треугольников мы использовали только определения основных тригонометрических функций. Для решения же косоугольных треугольников нам потребуется знание зависимостей между сторонами и тригонометрическими функциями углов косоугольных треугольников, известные как теоремы синусов, косинусов и тангенсов. К выводу этих теорем мы и переходим.
В дальнейшем мы будем пользоваться следующими обозначениями: a, b и с — стороны треугольника; А, В и С — противолежащие им углы; S — площадь; 2р — периметр; R — радиус описанного круга; r — радиус вписанного круга; hа, lа и mа — высота, биссектриса и медиана, соответствующие стороне а.
Теорема. Во всяком треугольнике стороны пропорциональны синусам противолежащих углов:
Если угол А острый, то А = А’, так как вписанные углы A и A’ опираются на одну и ту же дугу.
Если угол А тупой, то угол А’ острый, измеряющийся половиной дуги ВАС:
Итак, или A = А’, или A’ = 
Если угол A прямой, то а = 2R, sin A = 1 и равенство (1) также справедливо.
Аналогичные равенства найдём и для прочих углов В и С. Итак,
а = 2R sin A; b = 2R sin В; с = 2R sin С, откуда

Следствие. Отношение стороны треугольника к синусу противолежащего угла равно диаметру круга, описанного около треугольника.
2. Теорема косинусов
Теорема. Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Доказательство. Докажем первое равенство.
Случай 1. Угол A острый.
Из треугольника АВН найдём:
АН = с cos / BAH= с cos ( 
Подставив в формулу (2), получим доказываемое равенство.
Случай 3. Угол А прямой.
Итак, во всех случаях
3. Формулы для вычисления площади треугольника
2. Теорема. Площадь треугольника равна половине произведения двух сторон на синус угла между ними:
Доказательство. Из геометрии известно, что площадь треугольника равна половине произведения стороны треугольника на высоту, опущенную на эту сторону из противоположной вершины.
Если угол А острый, то из треугольника АВН найдём ВН = hb = с sin A.
Если угол A тупой, то ВН = hb = с sin ( 
hb = АВ = с = с sin A.
Следовательно, во всех случаях hb = с sin A. Подставив в равенство (1), получим доказываемую формулу.
Точно так же получим формулы: S = 1 /2 ab sin C = 1 /2 ac sin B
3. На основании теоремы синусов:
Подставив эти выражения в формулу (1), получим следующую формулу:
Теорема. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов:
(и две аналогичные формулы для прочих пар сторон а, с и b, с).
Доказательство. В силу теоремы синусов имеем:
Разделив почленно эти равенства, получим доказываемую формулу.
5.Решение треугольника по двум его углам и стороне
Задача. Даны два угла треугольника и сторона, прилежащая к ним; вычислить другие стороны и угол.Даны В, С и а; требуется найти b, с и А.
Решение. Условие возможности построения треугольника по этим данным: А + В / а 2 + b 2 — 2ab cos С
Для вычисления А можно также воспользоваться формулой косинусов:
Так как 0 b, т. е, заданный угол А лежит против большей стороны.
Построение показано на чертеже. Из точки С (как из центра), взятой на одной из сторон угла А на расстоянии b от вершины, описана окружность радиуса а; точка В есть точка пересечения этой окружности с другой стороной угла А.
Построение всегда возможно, задача имеет единственное решение.
Острый угол В, противолежащий меньшей стороне, находится по теореме синусов:
откуда
и затем С = 180° — (A + В). Сторона с находится по теореме синусов:
Значения угла В вычисляются по теореме синусов:
Из чертежа b) видно, что при CD = b sin А > а окружность не пересечёт другой стороны угла А; задача не имеет решений.
В этом случае 
При CD = b sin А задача имеет единственное решение: треугольник ABC прямоугольный.
Случай 3. а = b. В этом случае треугольник ABC равнобедренный. Такой треугольник можно решить, разбразбив его высотой CD на два прямоугольных треугольника:
В = А; С = 180° — 2А; с = 2AD = 2а cos A.
8.Решение треугольника по трём сторонам
Задача. Даны три стороны треугольника; вычислить его углы.
Имеем далее: S = 1 /2 bc sin A. откуда
Угол А острый, так как он лежит против меньшей стороны; следовательно,

Как решить косоугольный треугольник
О РЕШЕНИИ ТРЕУГОЛЬНИКОВ.
X. Косоугольные треугольники.
§ 97. Соотношения между элементами косоугольного треугольника.
Начнем с геометрического соотношения между углами треугольника:
Заметим некоторые следствия из него.
а) Так как сумма значений А и В + С равна 180°, то синусы их равны, а косинусы различаются знаками; поэтому
sin (B + C) = sin A; cos (B+C)= — cos A; cos A = — cos <В + С).
б) Так как сумма значений 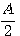
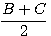
sin 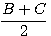
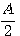
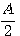
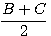
в) Полезно запомнить еще следующие соотношения между угламя треугольника:
l) sin A + sin B + sin С = 4 cos 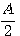
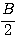
2) tg A + tg B+ tg C = tg A • tg B • tg C;
3) ctg 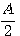
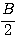
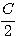
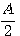
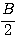
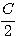
Вывод этих формул предоставляется учащемуся.
§ 98. Лемма. Во всяким треугольнике сторона равна диаметру описанного круга, умноженному на синус противолежащего угла.
Обозначая радиус описанного круга через R, докажем, например, что а = 2R • sin A, где угол А есть острый или тупой.
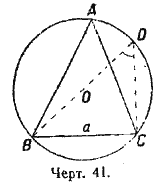
Доказательство. 1) Угол А острый (черт. 41). В oписанном круге из конца данной стороны проведем диаметр и соединим другие концы этой стороны и диаметра; получим прямоугольный треугольник. На чертеже 41 таким треугольником будет BDC; из него, на основании § 21, находим: BC = BD • sin D, или a = 2R• sin D; нo / D = / А 1) ; следовательно, a = 2R• sin A.
1) Тот и другой измеряются половиной дуги ВС.
2) Угол А тупой. Сделаем такое же вспомогательное построение, как раньше. Из прямоугольного треугольника ВСЕ (черт. 42) найдем: a = 2R• sin E; но Е + А = 180°, следовательно sin E = sin A, поэтому a = 2R• sin A. Итак, вообще:
a = 2R• sin A; b = 2R• sin B; c = 2R• sin C.
§ 99. Теорема. Во всяком треугольнике стороны пропорциональны синусам противолежащих углов.
Требуется доказать, что:
Доказательство. По § 98 для всякого треугольника как остроугольного, так и тупоугольного имеем:
a = 2R• sin A; b = 2R• sin B; c = 2R• sin C.
Таким образом, для одного и того же треугольника частное от деления стороны на синус противолежащего угла есть величина постоянная, равная диаметру описанного круга.
a : b : c = sin A : sin B : sin С,
т. е. во всяком треугольнике стороны, относятся между собой, как синусы противолежащих углов.
Пример. Определить a : b : c, если А : В : С= 3 : 4 : 5.
Так как А + В + С =180°, то сначала разделим 180° в отношении 3 : 4 : 5; получим
А = 45°, B = 60° и С = 75°. Теперь по доказанному будем иметь:
a : b : c = sin 45° : sin 60° : sin 75°.
Подставляя сюда _ _
sin 45° = √ 2 /2, sin 60° = √ 3 /2 и sin 75° = cos 30° /2= 1 /2
получим, освободясь от знаменателей:
a : b : c = √ 2 : √ 3 : 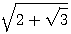
§ 100. Теорема. Сумма двух сторон треугольника так относится к их разности, как тангенс полусуммы противолежащих углов относится к тангенсу полуразности тех же углов.
Доказательство. По §98 находим:
a + b = 2R
Применяя здесь ко второй части формулу (XVII) (§ 65), получим:
( a + b ) : (а — b ) = tg 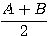
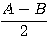
чем и выражается теорема.
§ 101. Формулы Мольвейде. Так называются следующие две пропорции, которые содержат отношения суммы и разности двух сторон треугольника к третьей стороне:
Доказательство. 1) По §98:
a + b = 2R (sin A + sin B) и c = 2R • sin C;
Преобразуем вторую часть:
но sin 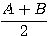
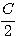
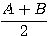
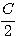
2) Таким же образом получим:
§ 102. Теорема. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения их на косинус угла между ними.
Требуется доказать, что а 2 = b 2 + с 2 — 2bс • соs A (одинаково и в случае острого и в случае тупого;
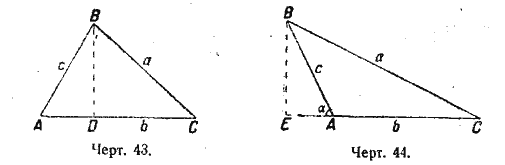
Доказательство. 1) Если угол А острый, то на основании теоремы геометрии о квадрате стороны, лежащей против острого угла, имеем (черт. 43):
но из прямоугольного треугольника ABD можно заменить AD через с • cos A; тогда получим:
2) Если угол A тупой, то применяем теорему о квадрате стороны против тупого угла треугольника (черт. 44). Получаем
Из треугольника ABC находим:
cos α = cos (180° — А) = — cos A,
Подставляя это выражение в геометрическую формулу, получим: