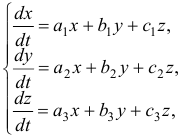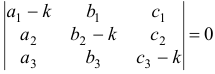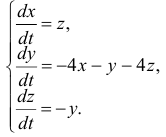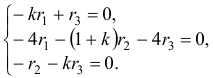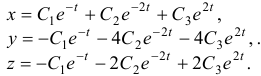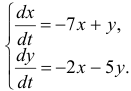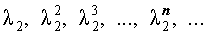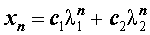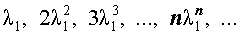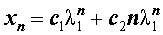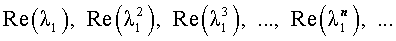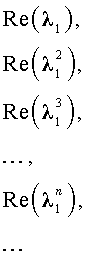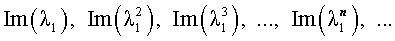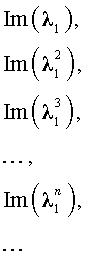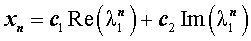Как решить характеристическое уравнение
Решение систем дифференциальных уравнений с помощью характеристического уравнения
Пусть дана однородная система
где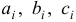 
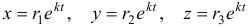
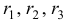
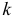
— постоянные. Будем искать частные решения системы в виде 
, где 
и 
— неопределенные коэффициенты, которые следует найти. Уравнение
называется характеристическим уравнением системы. Отыскав корни этого уравнения, и поочередно подставляя их в исходную систему, определим коэффициенты .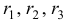
Пример №1
Найти общее решение системы
Решение:
Система в данном случае имеет вид: 
Характеристическое уравнение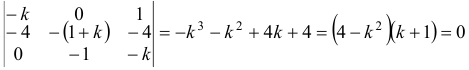 
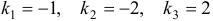
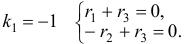
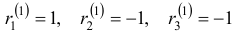
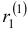
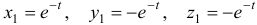
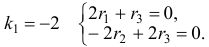
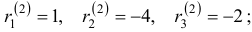
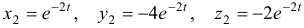
имеет корни 
. Для 
Решением этой системы будут, например, числа 
(здесь 
выбрано произвольно). Следовательно, 
. Для 
Решая эту систему, получим 
тогда 
.
Наконец, для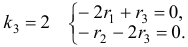 
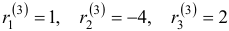
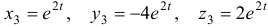
Здесь можно положить 
и будем иметь 
.
Общее решение данной системы дифференциальных уравнений таково:
Пример №2
Решение:
Чаще системы дифференциальных уравнений записывают в виде: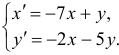 
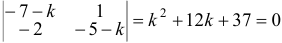
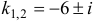
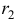
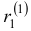
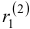
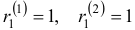
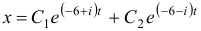
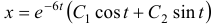
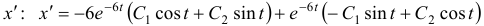
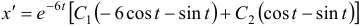
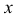
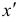
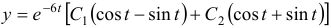
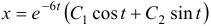
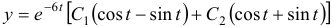
Составим характеристическое уравнение 
и найдем его корни 
. Так как эти корни комплексные, система уравнений будет иметь комплексные коэффициенты и даст комплексные значения для чисел 
и 
. В этом случае, учитывая возможность произвольного выбора 
и 
, целесообразно сразу положить 
и, записав функцию 
или, что то же самое, 
, найти функцию 
, используя первое уравнение системы: 
. Для этого найдем 
или 
. Подставляя 
и 
в первое уравнение системы, получим 
. Общим решением системы будет 
и 
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Возможно вам будут полезны эти страницы:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Возвратные последовательности:
рекуррентная формула, характеристическое уравнение
 Определение возвратной последовательности |
| Характеристическое уравнение |
| Общее решение рекуррентного уравнения 2-го порядка |
| Схема вывода формулы общего члена возвратной последовательности второго порядка |
| Примеры с решениями |
Определение возвратной последовательности
в каждой из которых символами b1 и q обозначены заданные числа – первый член и знаменатель прогрессии.
а остальные члены последовательности определяются с помощью рекуррентной формулы (рекуррентного уравнения)
– заданные числа ( коэффициенты рекуррентной формулы ).
Характеристическое уравнение
удовлетворяет рекуррентной формуле (1).
то при подстановке формул (2) и (3) в формулу (1) возникает уравнение
которое удобно переписать в виде
Общее решение рекуррентного уравнения второго порядка
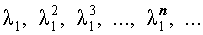
и 
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
также удовлетворяет рекуррентной формуле (1).
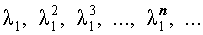
и 
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
также удовлетворяет рекуррентной формуле (1).
В случае, когда характеристическое уравнение имеет два комплексно-сопряженных корня λ1, 2 = α ± i β, каждая из последовательностей
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
также удовлетворяет рекуррентной формуле (1).
Ряд примеров, в которых выводятся формулы общего члена возвратных последовательностей, разобран в разделе «Возвратные последовательности: вывод формулы общего члена» нашего справочника.
будет иметь характеристическое уравнение вида
имеет характеристическое уравнение
Характеристические корни (корни характеристического уравнения) также предоставляют качественную информацию о поведении переменной, эволюция которой описывается динамическим уравнением. Для дифференциального уравнения, параметризованного по времени, эволюция переменной стабильна тогда и только тогда, когда действительная часть каждого корня отрицательна. Для разностных уравнений существует стабильность тогда и только тогда, когда модуль ( абсолютное значение ) каждого корня меньше 1. Для обоих типов уравнений постоянные флуктуации возникают, если имеется хотя бы одна пара комплексных корней.
СОДЕРЖАНИЕ
Вывод
Поскольку e rx никогда не может быть равным нулю, его можно разделить, дав характеристическое уравнение
Формирование общего решения
y ( Икс ) знак равно y D ( Икс ) + y р 1 ( Икс ) + ⋯ + y р час ( Икс ) + y C 1 ( Икс ) + ⋯ + y C k ( Икс ) <\ displaystyle y (x) = y _ <\ mathrm 
Пример
Линейное однородное дифференциальное уравнение с постоянными коэффициентами
имеет характеристическое уравнение
По факторинговых характеристическое уравнение в
Отчетливые настоящие корни
y D ( Икс ) знак равно c 1 е р 1 Икс + c 2 е р 2 Икс + ⋯ + c п е р п Икс <\ displaystyle y _ <\ mathrm
Повторяющиеся настоящие корни
d k d Икс k ( ты ) знак равно ты ( k ) знак равно 0 <\ displaystyle <\ frac
Сложные корни
y C ( Икс ) знак равно е а Икс ( C 1 потому что б Икс + C 2 грех б Икс ) <\ displaystyle y _ <\ mathrm
Этот анализ также применяется к частям решений дифференциального уравнения высшего порядка, характеристическое уравнение которого включает невещественные комплексно сопряженные корни.
Как решить характеристическое уравнение
Характеристическое уравнение составляется для цепи после коммутации. Оно может быть получено следующими способами:
Согласно первому способу в предыдущей лекции было получено дифференциальное уравнение относительно напряжения 
на конденсаторе для последовательной R-L-C-цепи, на базе которого записывается характеристическое уравнение.
Следует отметить, что, поскольку линейная цепь охвачена единым переходным процессом, корни характеристического уравнения являются общими для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение. Поэтому по первому способу составления характеристического уравнения в качестве переменной, относительно которой оно записывается, может быть выбрана любая.
Применение второго и третьего способов составления характеристического уравнения рассмотрим на примере цепи рис. 1.
Составление характеристического уравнения по методу входного сопротивления заключается в следующем:
записывается входное сопротивление цепи на переменном токе;
j w заменяется на оператор р;
полученное выражение 
приравнивается к нулю.
совпадает с характеристическим.
Следует подчеркнуть, что входное сопротивление может быть записано относительно места разрыва любой ветви схемы. При этом активный двухполюсник заменяется пассивным по аналогии с методом эквивалентного генератора. Данный способ составления характеристического уравнения предполагает отсутствие в схеме магнитосвязанных ветвей; при наличии таковых необходимо осуществить их предварительное развязывание.
Для цепи на рис. 1 относительно зажимов источника
.
Заменив j w на р и приравняв полученное выражение к нулю, запишем
 . | (1) |
При составлении характеристического уравнения на основе выражения главного определителя число алгебраических уравнений, на базе которых он записывается, равно числу неизвестных свободных составляющих токов. Алгебраизация исходной системы интегро-дифференциальных уравнений, составленных, например, на основании законов Кирхгофа или по методу контурных токов, осуществляется заменой символов дифференцирования и интегрирования соответственно на умножение и деление на оператор р. Характеристическое уравнение получается путем приравнивания записанного определителя к нулю. Поскольку выражение для главного определителя не зависит от правых частей системы неоднородных уравнений, его составление можно производить на основе системы уравнений, записанных для полных токов.
Для цепи на рис. 1 алгебраизованная система уравнений на основе метода контурных токов имеет вид
Отсюда выражение для главного определителя этой системы
.
Приравняв D к нулю, получим результат, аналогичный (1).
Общая методика расчета переходных процессов классическим методом
В общем случае методика расчета переходных процессов классическим методом включает следующие этапы:
Примеры расчета переходных процессов классическим методом
1. Переходные процессы в R-L цепи при ее подключении к источнику напряжения
Такие процессы имеют место, например, при подключении к источнику питания электромагнитов, трансформаторов, электрических двигателей и т.п.
Рассмотрим два случая:
а) 
б) 
.
Согласно рассмотренной методике для тока в цепи на рис. 2 можно записать
 . | (3) |
Тогда для первого случая принужденная составляющая тока
 . | (4) |
,
откуда 
и постоянная времени 
.
 . | (5) |
Подставляя (4) и (5) в соотношение (3), запишем
.
В соответствии с первым законом коммутации 
. Тогда
,
откуда 
.
Таким образом, ток в цепи в переходном процессе описывается уравнением
,
а напряжение на катушке индуктивности – выражением
.
Качественный вид кривых 
и 
, соответствующих полученным решениям, представлен на рис. 3.
При втором типе источника принужденная составляющая рассчитывается с использованием символического метода:
,
где 
.
.
Выражение свободной составляющей не зависит от типа источника напряжения. Следовательно,
.
Поскольку 
, то
.
Таким образом, окончательно получаем
 . | (6) |
Анализ полученного выражения (6) показывает:
Если 
значительна по величине, то за полпериода свободная составляющая существенно не уменьшается. В этом случае максимальная величина тока переходного процесса 
может существенно превышать амплитуду тока установившегося режима. Как видно из рис. 4, где
, максимум тока имеет место примерно через 
. В пределе при 
.
Таким образом, для линейной цепи максимальное значение тока переходного режима не может превышать удвоенной амплитуды принужденного тока: 
.
Аналогично для линейной цепи с конденсатором: если в момент коммутации принужденное напряжение равно своему амплитудному значению и постоянная времени 
цепи достаточно велика, то примерно через половину периода напряжение на конденсаторе достигает своего максимального значения 
, которое не может превышать удвоенной амплитуды принужденного напряжения: 
.
2. Переходные процессы при отключении катушки индуктивности от источника питания
При размыкании ключа в цепи на рис. 5 принужденная составляющая тока через катушку индуктивности 
.
,
откуда 
и 
.
В соответствии с первым законом коммутации
.
Таким образом, выражение для тока в переходном режиме
и напряжение на катушке индуктивности
 . | (7) |
Анализ (7) показывает, что при размыкании цепей, содержащих индуктивные элементы, могут возникать большие перенапряжения, которые без принятия специальных мер могут вывести аппаратуру из строя. Действительно, при 
модуль напряжения на катушке индуктивности в момент коммутации будет во много раз превышать напряжение источника: 
. При отсутствии гасящего резистора R указанное напряжение прикладывается к размыкающимся контактам ключа, в результате чего между ними возникает дуга.
3. Заряд и разряд конденсатора
При переводе ключа в положение 1 (см. рис. 6) начинается процесс заряда конденсатора:
.
Принужденная составляющая напряжения на конденсаторе 
.
Из характеристического уравнения
определяется корень 
. Отсюда постоянная времени 
.
.
При t=0 напряжение на конденсаторе равно 
(в общем случае к моменту коммутации конденсатор может быть заряженным, т.е. 
). Тогда 
и
.
Соответственно для зарядного тока можно записать
.
При разряде конденсатора на резистор 
(ключ на рис.6 переводится в положение 2) 
. Постоянная времени 
.
Тогда, принимая, что к моменту коммутации конденсатор был заряжен до напряжения 
(в частном случае 
), для напряжения на нем в переходном режиме можно записать
.
Соответственно разрядный ток
 . | (8) |
Как видно из (8), во избежание значительных бросков разрядного тока величина 
должна быть достаточно большой.
В заключение отметим, что процессы заряда и разряда конденсатора используются в генераторах пилообразного напряжения, широко применяемых в автоматике. Для этого ключ в схеме на рис. 6 заменяется на электронный.
Ответ: 
.
Ответ: 
.