Как решаются текстовые задачи
Как решать текстовые задачи по математике ЕГЭ
Текстовые задачи ― это одни из самых нелюбимых заданий, особенно у учеников старших классов, потому что чем дальше, тем запутаннее становится условие, тем сложнее становится составить уравнение и верно решить задачу. Но, как и в любой теме в математике, чтобы уверенно решать сложные задачи, необходимо разобраться с самыми основными приемами.
Примеры решения текстовых задач из ЕГЭ
Разберем эти задачи с самого начала. Текстовая задача состоит из условия, в котором описана некоторая ситуация, и вопроса, на который нужно дать ответ.
Задача: Коля наклеил на 5 листов по 2 наклейки. Сколько наклеек наклеил Коля?
Условие: Коля наклеил на 5 листов по 2 наклейки.
Вопрос: Сколько наклеек наклеил Коля?
Решение любой текстовой задачи можно разделить на несколько основных этапов:
Для одного уравнения может быть составлено множество различных условий.
Пример:
Уравнение: 2 + х = 5.
Условие 1: Маша и Петя вместе нашли 5 грибов. Маша нашла 2. Сколько грибов нашел Петя?
Условие 2: Букет состоит из ромашек и колокольчиков. Всего в букете 5 цветков, из них 2 ромашки. Сколько колокольчиков в букете?
Условие 3: На елке было 5 игрушек. Две из них упали и разбились. Сколько игрушек осталось на елке?
Для облегчения работы с условием полезно использовать иллюстрацию или моделирование. Это может быть краткая запись условия математически или словесно. Также это может быть дополнительный рисунок или таблица.
Задача: Петя выше Коли, Сережа ниже Коли. Кто выше?
Из рисунка сразу понятен ответ: Петя выше всех.
Для составления уравнения по условию задачи используются различные приемы, в зависимости от данной в условии зависимости величин.
Алгебраическая зависимость в текстовых задачах
Такая зависимость выражается в словах: выше/ниже, больше/меньше, дороже/дешевле, длиннее/короче и т. д.
При составлении уравнения особое значение играют используемые предлоги: «в» и «на».
Задача: Петя выше Коли на 20 см, Сережа ниже Коли на 10 см. На сколько см Петя выше Сережи?
Решение: Пусть П ― рост Пети, К ― рост Коли, С ― рост Сережи.
Кстати, обратите внимание на этот приём ― выбирать «говорящие» переменные, а не безликие иксы и игреки, чтобы не запутаться при работе с уравнением.
Выразим рост мальчиков.
Петя выше Коли на 20 см: П – 20 = К.
Сережа ниже Коли на 10 см: К = С + 10.
Подставим в первое уравнение рост Коли: П – 20 = С + 10.
Нам нужно найти, на сколько см Петя выше Сережи: П – С.
П – 20 = С + 10;
П – С = 20 + 10;
П – С = 30.
Получаем, что Петя выше Сережи на 30 см.
Задача: На уроке труда ученики делали снежинки. Всего было сделано 12 снежинок. Маша сделала в два раза больше снежинок, чем Коля. Коля сделал на 4 снежинки меньше, чем Рома. Сколько снежинок сделала Маша?
Решение:
Пусть М ― количество снежинок, которое сделала Маша, К – снежинки Коли, Р ― снежинки Ромы.
Маша сделала в два раза больше снежинок, чем Коля: К = М/2.
Коля сделал на 4 снежинки меньше, чем Рома: Р = К + 4 = М/2 + 4.
Вместе ребята сделали 12 снежинок: М + К + Р = 12.
Подставим все выраженные через М значения: М + М/2 + М/2 + 4 = 12.
М = 4.
Маша сделала 4 снежинки.
Процентная зависимость
Процент ― это всегда доля какого-то числа.
100% ― все число;
50% ― половина;
25% ― четверть.
Чтобы найти 1%, необходимо поделить всё число на 100.
Задача:
Есть 100 яблок.
1% от всех яблок 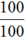
Есть 200 груш.
1% от всех груш ― 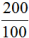
Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом ― соответствующие проценты.
Пример:
200 груш ― 100 %;
2 груши ― 1 %.
Прогрессия отражает зависимость величин. По-другому это можно записать в виде двух дробей: 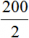
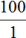
Исходя из правил работы с дробями, получаем правила работы с пропорцией:
Задачи
1. Альбом, который стоил 140 рублей, продаётся с 30%-ой скидкой. При покупке 4 таких альбомов покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить?
Решение: Новая стоимость альбома равна 140 ∙ (1 – 0,3) = 140 ∙ 0,7 = 98 рублей, тогда при покупке 4 таких альбомов покупатель потратит 98 ∙ 4 = 392 рубля. И сдача равна 500 – 392 = 108 рублей.
2. Государству принадлежит 70% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 50 млн. р. Какая сумма (в млн. рублей) из этой прибыли должна пойти на выплату частным акционерам?
Решение: Запишем все данные в виде таблицы:
| Государству | Частным лицам | Общее | |
| Проценты | 70% | 30% | 100% |
| Абсолютное значение | ? | 50 млн. руб. |
100% ― 50 млн. рублей;
Тогда можем легко посчитать сумму, которая должная пойти на выплату частным акционерам, взяв 3 раза по 10%:
3 ∙ 5 = 15 млн. рублей.
| Государству | Частным лицам | Общее | |
| Проценты | 70% | 30% | 100% |
| Абсолютное значение | 35 млн. руб. | 15 млн. руб. | 50 млн. руб. |
3. Задача. Товар на распродаже уценили на 40%, при этом он стал стоить 750 р. Сколько рублей стоил товар до распродажи?
Решение: Имеем формулу для цены товара, который уценивают:
первоначальная цена (1 ― величина скидки в долях) = новая цена.
Подставим то, что нам дано по условию:
первоначальная цена (1 – 0,4) = 750;
первоначальная цена = 750 : 0,6;
первоначальная цена = 1250.
4. Задача. Из объявления фирмы, проводящей обучающие семинары: «Стоимость участия в семинаре ― 1500 рублей с человека. Группам от организаций предоставляются скидки: от 4 до 8 человек ― 10%; более 8 человек ― 15%».
Сколько рублей должна заплатить организация, направившая на семинар группу из 8 человек?
Решение: Стоимость семинаров для группы без скидки равна 1500 ∙ 8 = 12000. Скидка будет составлять 10%, так как по условию именно такая скидка для групп из 8 человек. 10% от 12000 ― это 1200, значит, стоимость со скидкой будет: 12000 – 1200 = 10800.
5. Задача. Поступивший в продажу в январе мобильный телефон стоил 4800 рублей. В марте он стал стоить 3840 рублей. На сколько процентов снизилась цена на мобильный телефон в период с января по март?
Решение: Цена за телефон снизилась на 4800 – 3840 = 960 рублей. Поделим эту разницу на цену в январе: 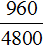
Значит, цену снизили на 0,2 ∙ 100% = 20%.
6. Задача. Апельсины подешевели на 20%. Сколько апельсинов (в кг) можно теперь купить на те же деньги, на которые раньше покупали 4,8 кг?
Решение: Нам не дана стоимость 1 кг апельсин, поэтому возьмем удобное для вычисления число, например, пусть 1 кг апельсин стоил 100 рублей. Тогда сейчас он стоит 100 ∙ (1 – 0,2) = 80 рублей. Количество денег, на которое мы покупали 4,8 кг апельсин легко посчитать : 4,8 ∙ 100 = 480 рублей. Таким образом, сейчас мы можем купить на эти деньги 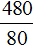
7. Задача. На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 35 рублей за штуку. У Вани есть 160 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения?
Решение. Делим 160 на 35, получаем 4 целых. Но Ване нужно купить нечетное число цветов, поэтому в ответе указываем 3.
8. Задача. Сырок стоит 6 рублей 70 копеек. Какое наибольшее число сырков можно купить на 50 рублей?
Решение. Переведем все в копейки. Сырок стоит 670 копеек, а у нас имеется 5000 копеек. Делим 5000 на 670 и получаем 7, 46…Так как часть сырка купить нельзя, округляем в меньшую сторону до целого ― 7 сырков.
Решение текстовых задач на уроках алгебры. 9-й класс
Разделы: Математика
Класс: 9
систематизировать знания и умения учащихся решать текстовые задачи.
совершенствование, развитие, углубление знаний, умений, навыков по решения текстовых задач;
развитие мыслительной деятельности: умение анализировать, обобщать, сравнивать;
развитие творческой деятельности: смекалки;
развитие математической речи и графической культуры, памяти
формирование мировоззрения с помощью взаимосвязанной системы знаний по данной теме;
формирование обще учебных навыков: вычислительных, эстетических навыков при оформлении записей;
формирование качеств личности: трудолюбия, самостоятельности, стремления к самореализации.
Ожидаемые результаты обучения:
В результате повторения данных тем учащиеся:
• закрепляют знания о рациональных уравнениях, понятие “решение уравнения”, понятие “решение системы уравнений”,
• развивают способности к анализу и синтезу изучаемого материала, умение выделять главное в тексте учебника,
• воспитывают волю и настойчивость при решении, желание добиться результата.
Тип урока: урок комплексного применения ЗУН.
Форма организации урока: урок-практикум.
Ход урока
Решаем устно задания из бока “Реальная математика”
Найдите 30% от 27. (0,9)
Какое число получится, если 140 увеличить на 60%? (224)
Кафельная плитка продается коробками по 6 м2. Сколько коробок плитки нужно купить, чтобы хватило на облицовку стен площадью 35 м2? (6)
Билеты в ботанический сад стоит 50 рублей. Сколько рублей сдачи нужно получить с 2000 рублей, заплаченных за проход 36 человек? (200)
Горные лыжи стоят 16 000 рублей. Сколько рублей будут стоить горные лыжи во время сезонной распродажи, когда на них объявлена скидка 20%? (12800)
1. Задачи на движение.
В настоящее время на экзамене по математике в блоке “алгебра” предлагаются задачи, решение которых требует составления уравнения, а также их систем на основании условия задачи.
Указания к задачам:
1.Основными компонентами этого типа являются:
а) пройденный путь (S);
2. Зависимость между величинами выражается известными формулами:
S=v/t; v=S/t; t=S/v.(Указанные величины должны быть в одной системе единиц, например: путь в км, время в часах, то скорость в км/час.)
Из А в В по течению реки отправился плот. А через час вслед за ним отправилась яхта, которая, прибыв в пункт В тотчас повернула обратно и возвратилась в А. К этому времени плот удалился от А на расстояние 24 км. Пристань А расположена в 120 км от пристани В. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
1. Заполните таблицу.
| S (км) | v (км/ч) | t (ч) | |
| Плот | 120 | 2 | 60 |
| Яхта (по течению) | 120 | Х+2 | 120/х+2 |
| Яхта (против течения) | 120 | Х-2 | 120/х-2 |
2. Составим и решим уравнение:
Х1= (240+244)/22=22; х2 = (240-244)/22=-4/22 – не удовлетворяет условию задачи.
Пристани А и В расположены на реке, скорость течения которой на этом участке равна 4 км/ч. Лодка проходит от А до В и обратно без остановок со средней скоростью 6 км/ч. Найти собственную скорость лодки.
Пусть х км/ч – собственная скорость лодки.
Получим х=8 км/ч или х=-2(не удовлетворяет условию задачи)
2. Задачи на совместную работу.
Алгоритм решения задач на совместную работу
Принимаем всю работу, которую необходимо выполнить за 1.
Находим производительность труда каждого рабочего в отдельности, т.е., где t – время, за которое этот рабочий может выполнить всю работу, работая отдельно.
Находим ту часть всей работы, которую выполняет каждый рабочий отдельно за то время, которое он работал.
Составляем уравнение, приравнивая объем всей работы к сумме слагаемых, каждое из которых есть часть всей работы, выполненная отдельно каждым из рабочих.
Первая бригада может выполнить задание за 20 часов, а вторая – за 30 часов. Сначала бригады выполнили при совместной работе 3/4 задания, а остальную часть задания выполнила одна первая бригада. За сколько часов было выполнено задание?
Две трубы, работая вместе, наполнили бассейн за 12 часов. Первая труба, работая отдельно, наполняет бассейн на 18 часов быстрее, чем вторая. За сколько часов наполняет бассейн вторая труба.
Х1=36; Х2 =6 (не удовлетворяет условию задачи)
3. Задачи с использованием формул двузначного числа
Алгоритм решения задач, в которых используется формула двузначного числа.
Искомое двузначное число 10х + у
Составить систему уравнений.
Двузначное число в четыре раза больше суммы его цифр. Если к этому числу прибавить произведение его цифр, то получится 32. Найдите это двузначное число.
Х – цифра десятков. У – цифра единиц. 10х + у – искомое число.
х1 =-8 (посторонний корень)
Найти двузначное число, которое в 2 раза больше суммы его цифр и в 2,25 раза больше произведения его цифр.
Пусть число ху =10х+у, тогда составим систему:
18х(х-1)=0, х1=0 (не удовлетворяет условию задачи).
и х2 =1, у=8, искомое число 18.
4. Задачи на смеси и растворы.
Алгоритм решения задач на смеси.
х – масса первого раствора, у – масса второго раствора, (х + у) – масса полученной смеси.
Найти содержание растворенного вещества в растворах, т.е.
а % от х, в % от у, с % от (х+у)
Составить систему уравнений.
Задача 1
Смешали 30%-й раствор соляной кислоты с 10%-м и получили 600 г 15%-го раствора. Сколько граммов каждого раствора было взято?
Введем обозначение. Пусть взяли х г первого раствора, у г – второго раствора, тогда масса третьего раствора – (х+у).
Определим количество растворенного вещества в первом, втором, третьем растворах, т.е. найдем 30% от х, 10% от у, 15% от 600.
Составим систему уравнений:
х = 150, у = 600 – 150 = 450
Ответ: взяли 150 г первого раствора и 450 г второго раствора.
III. Подведение итогов урока (4 минуты)
Ребята вы сегодня от души потрудились, порадовали меня своими знаниями. У кого 4 и более жетончиков подойдите с дневниками. Проставляю оценки в журнал:
IV. Домашнее задание
1. Моторная лодка прошла 48 км по течению реки, и вернулся обратно, потратив на весь путь 7 часов. Скорость течения реки равна 2 км/час. Скорость течения реки равна 2 км/час. Найдите скорость лодки в неподвижной воде.
2. Две машины, работая вместе, могут расчистить каток за 20 минут. Если первая машина будет работать 25 минут, а затем её сменит вторая, то она закончит расчистку катка через 16 минут. За сколько времени может расчистить каток каждая из машин, работая отдельно?
В обучении математике текстовые задачи всегда занимали особое место. Пока мы будем учить детей на русском языке – не только великом и могучем, но и достаточно трудном, пока мы хотим учить их сравнивать, выбирать наиболее простой путь достижения поставленной цели, пока мы не отказались от воспитания гибкости и критичности мышления, пока мы стараемся увязывать обучение математике с жизнью, нам будет трудно обойтись без текстовых задач.
Сегодня на уроке …
Теперь я знаю …
Мне на уроке …
Активно на уроке работали …
Старались …
Жду большей активности от …
Как решаются текстовые задачи
Так как лап на 10 больше чем ушей.
Составим и решим уравнение:4х – 2х = 102х= 10 │: 2х = 5
Ответ: 5 кошек грелось на солнышке.
способ
1. На сколько лап больше чем ушей у одной кошки?4 – 2 = 2 (шт.)
2. Сколько кошек грелось на солнышке?10 : 2 = 5 (шт.)
Ответ: 5 кошек грелось на солнышке.
Задача7. В хозяйстве имеются куры и овцы. Сколько тех и других, если известно, что у них вместе 19 голов и 46 ног?
Составленное уравнение учащиеся решают самостоятельно, с последующей проверкой.
Ответ: 15 кур, 4 овцы
Логический метод.
Задача 8. Кто из учеников Саша, Сергей, Дима и Андрей играет, а кто не играет в шахматы, если известно следующее:
а) если Саша и Сергей играет, то Дима не играет;
б) если Сергей не играет, то играют Дима и Андрей;
Если Саша и Сережа играют, то Дима не играет.
Если играют Дима и Андрей, то Сережа не играет.
Так как Дима по условию играет в шахматы, значит – это Дима и Андрей играют в шахматы.
Ответ: в шахматы играют ученики Дима и Андрей, а Саша и Сергей – не играют.
Задача 9. Поют в хоре и занимаются танцами 82 ученика, занимаются танцами и художественной гимнастикой 32 ученика, а поют в хоре и занимаются художественной гимнастикой 78 учеников. Сколько учеников поют в хоре, занимаются танцами и художественной гимнастикой отдельно, если известно, что каждый ученик занимается только чем-то одним?
1) 82 – 32 = 50 (чел.) –на столько больше учеников поют в хоре, чем
занимаются художественной гимнастикой;
4) 78 – 64 = 14 (чел.) — занимаются художественной гимнастикой;
Ответ: 64 ученика поют в хоре, 14 учеников занимаются художественной гимнастикой, 18 учеников занимаются танцами.
Среди учащихся 5 и 6 классов, в количестве 33 человек с предложенными задачами справилось 12 человек. Задачи на проценты в 5 классе учащиеся ещё не умеют решать. Обратились за помощью 8 учащихся, и потом они тоже справились с предложенными задачами.
Отсюда можно сделать вывод, что 37% успешно решили все задачи. Прибегнув к помощи, ещё 24% учащихся смогли справиться с данными задачами. Особые затруднения вызвали логические задачи.
Подводим итог: с задачами более простыми в целом ученики 5-го и 6-го классов справляются, но если добавляются немного больше элементов в рассуждениях, то справляются с такими заданиями не все.
Так же был проведён соц. Опрос среди учащихся 5-6 классов. Всем задавали вопрос: «Какие задачи легче решать: математические или логические?» В опросе участвовали 33 ученика. 25 учеников ответили – математические, 3 ученика – логические, 5 учеников – ни какие не могут решить.
Вывод: математические задачи легче решить 76-ти % опрошенных, логические – 10% и 14% не смогут решить никакую задачу.
Заключение
Для достижения цели данного исследования были выполнены следующие задачи:
1.Был произведен анализ некоторой методической и школьной литературы с точки зрения изучения методов решения задач в школе на уроках математики.
2.На основе изученного материла, были описаны методы и способы решения текстовых задач, в основной школе. С кратким описанием и приведением примеров.
3. В результате были описаны наиболее часто встречающиеся методы используемые в школьном курсе математики в 5 – 6 классах.
Таким образом, была достигнута цель данного исследования: описать методы и способы решения текстовой задачи в курсе изучения математики 5 – 6 классов.
Литература
1.Виленкин Н.Я. Математика: Учебник для 5 класса общеобразовательных учреждений// Н.Я.Виленкин, В.И. Жохов, А.С.Чесноков, С.И.Шварцбурд. – М.: Мнемозина: 1999-2004. – 384 с.
2.Виленкин Н.Я. Математика: Учебник для 6 класса общеобразовательных учреждений// Н.Я.Виленкин, В.И. Жохов, А.С.Чесноков, С.И.Шварцбурд. – М.: Мнемозина, 1999-2004. – 384 с.
3.Дорофеев Г.В. Математика 6 класс.-Просвещение,:2013.
5. Фридман, Л.М. Как научиться решать задачи [Текст] : Кн. для учащихся ст. кл. средн. шк. / Л.М. Фридман, Е.Н. Турецкий.– 3-е изд., дораб.– М.: Просвещение, 1989.– 192 с.: ил.
6. Целищева, И. Как помочь каждому ученику самост-но решать текстовые задачи [Текст] / И. Целищева, С. Зайцева // Нач. шк.: еженед. прил. к газ. «Первое сентября».– 2001.– 00.05 (№ 18).– С. 2-5.
Приложение
«ПАМЯТКА «КАК РЕШАТЬ ТЕКСТОВЫЕ ЗАДАЧИ»
1. Прочитай задачу и представь себе то, о чем в ней говорится.
2. Выдели условие и вопрос.
3. Запиши условие кратко или выполни чертёж.
4. Подумай можно ли сразу ответить на вопрос задачи. Если нет, то почему. Что надо узнать сначала, что потом?
5. Составь план решения.
7. Проверь решение и запиши ответ задачи.Примерный план ответа-рассуждения при решении задачи:
1.Арифметический метод.
1. Известно, что … (расскажи условие задачи)
2. Надо узнать… (повтори вопрос)
3. Чтобы ответить на вопрос задачи, надо …
4. Сразу мы не можем ответить на вопрос задачи, так как не знаем…
5. Поэтому в первом действии мы узнаем …
6. Во втором действии мы ответим на вопрос задачи. Для этого … ( какое действие выполняем)
2. Алгебраический метод:
Одним из важнейших направлений улучшения качества обучения математике является совершенствование его практической составляющей. К средствам реализации этого направления можно отнести использование текстовых задач и метода уравнений. Действительно, решение текстовых задач с помощью уравнений иллюстрирует применение математики к исследованию явлений реальной действительности, обеспечивает реализацию общих принципов прикладной направленности курса математики. Поэтому необходимо уделять внимание решению текстовых алгебраических задач. Схема работы над задачей:1 этап – анализ и запись условия задачи. Выполнение чертежа, если он необходим.
Содержание данного этапа включает:
Установление объекта наблюдения (исследования);
Выделение процессов, подлежащих рассмотрению;
Выявление величин, входящих в каждый процесс;
Выяснение функциональной зависимости между величинами и составление формул этой зависимости;
Схематическая запись условия задачи с обозначение неизвестных величин;
2 этап – нахождение плана решения.
Выявление основания для составления уравнения или системы уравнений;
Составление уравнения или системы уравнений;
3 этап – осуществление плана решения задачи.
Решение уравнения или системы;
Исследование корней уравнения (системы) с целью установления решений задачи. Проверка расчетов и обоснований;
4 этап – анализ решения задачи.Комментирование решения задачи. Возвращение к решению задачи (ретроспективный подход) с целью уточнения идей и методов решения задачи, упрощение расчетов. Поиск более рациональных приёмов решения задачи.
Памятка для лучшего усвоения решения задач с помощью уравнений.
Тщательно изучи условие задачи, если надо, сделай чертёж.
Выясни, о каких величинах идет речь в задаче.
Выбери любую из этих величин для правой части уравнения.
Установи, каким действием и над какими величинами её можно получить.
Выясни, какие из них известны, какие нет. Введи обозначение переменной.









