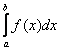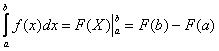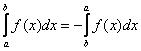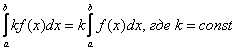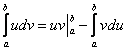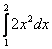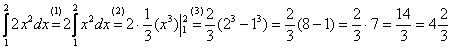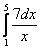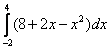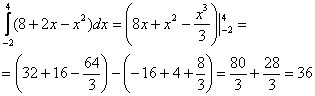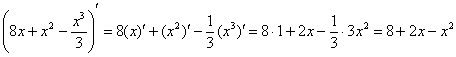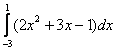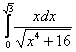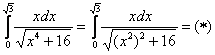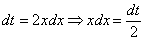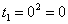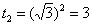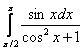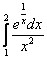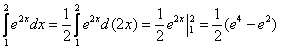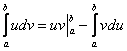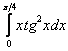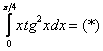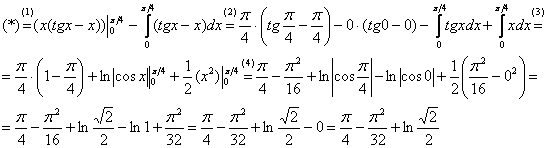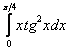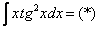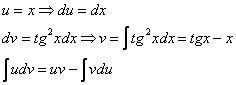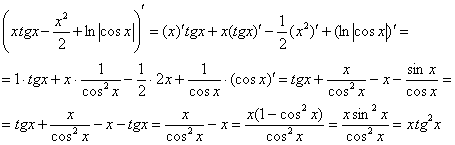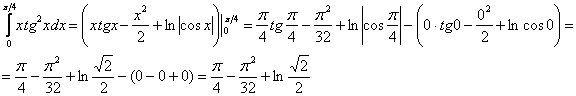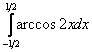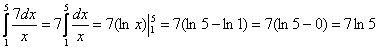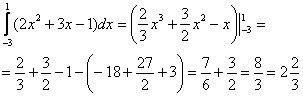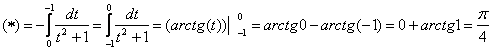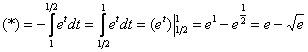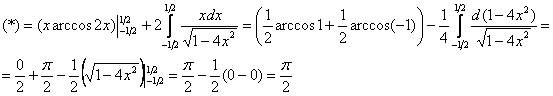Как решаются определенные интегралы
Определенный интеграл. Примеры решений
И снова здравствуйте. На данном уроке мы подробно разберем такую замечательную вещь, как определенный интеграл. На этот раз вступление будет кратким. Всё. Потому что снежная метель за окном.
Для того чтобы научиться решать определенные интегралы необходимо:
1) Уметь находить неопределенные интегралы.
2) Уметь вычислить определенный интеграл.
Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений. Кроме того, есть pdf-курсы для сверхбыстрой подготовки – если у вас в запасе буквально день, пол дня.
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования.
Нижний предел интегрирования стандартно обозначается буквой 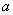
Верхний предел интегрирования стандартно обозначается буквой 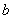
Отрезок 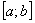
Прежде чем мы перейдем к практическим примерам, небольшое faq по определенному интегралу.
Что такое определенный интеграл? Считаю немного преждевременным рассказать про разбиения отрезка и предел интегральных сумм, поэтому пока я скажу, что определенный интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число.
Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла.
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.
Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница:
Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию 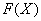
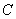
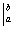
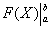
2) Подставляем значение верхнего предела в первообразную функцию: 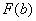
3) Подставляем значение нижнего предела в первообразную функцию: 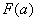
4) Рассчитываем (без ошибок!) разность 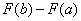
Всегда ли существует определенный интеграл? Нет, не всегда.
Например, интеграла 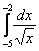
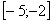
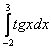
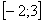
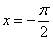
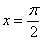
Для того чтобы определенный интеграл вообще существовал, достаточно чтобы подынтегральная функция была непрерывной на отрезке интегрирования.
Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования. По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?». В упрощенном варианте ситуация выглядит примерно так:
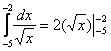
Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен интеграл вроде 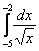
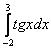
! Примечание: в последнем случае слово «определённого» опускать нельзя, т.к. интеграл с точечными разрывами разбивается на несколько, в данном случае на 3 несобственных интеграла, и формулировка «данного интеграла не существует» становится некорректной.
Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим отведена отдельная лекция.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может, и такая ситуация реально встречается на практике.
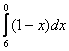
Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.
В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:
Например, в определенном интеграле перед интегрированием 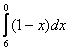
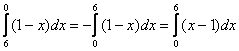
Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:
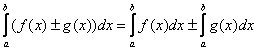
В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.
Для определенного интеграла справедлива формула интегрирования по частям:
Вычислить определенный интеграл
Решение:
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью самой популярной формулы 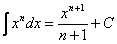
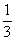
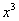
(3) Используем формулу Ньютона-Лейбница 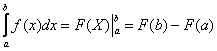
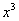
Вычислить определенный интеграл
Это пример для самостоятельно решения, решение и ответ в конце урока.
Немного усложняем задачу:
Вычислить определенный интеграл
Решение:
(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница: 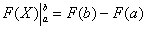
СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряю на третьем слагаемом: 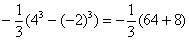
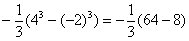
Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, я сам привык решать подобные интегралы так:
Здесь я устно использовал правила линейности, устно проинтегрировал по таблице. У меня получилась всего одна скобка с отчёркиванием пределов: 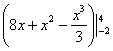
Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, но лично мне всё равно – обыкновенные дроби я считаю на калькуляторе.
Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту-чайнику лучше использовать первый способ, при «моём» способе решения точно где-нибудь потеряется знак.
Однако несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная 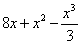
Совет: перед тем, как использовать формулу Ньютона-Лейбница, полезно провести проверку: а сама-то первообразная найдена правильно?
Так, применительно к рассматриваемому примеру: перед тем, как в первообразную функцию 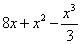
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден верно. Теперь можно и формулу Ньютона-Лейбница применить.
Такая проверка будет не лишней при вычислении любого определенного интеграла.
Вычислить определенный интеграл
Это пример для самостоятельно решения. Попробуйте решить его коротким и подробным способом.
Замена переменной в определенном интеграле
Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла. Таким образом, если с заменами у Вас не очень, следует внимательно ознакомиться с уроком Метод замены в неопределенном интеграле.
В этом параграфе нет ничего страшного или сложного. Новизна состоит в вопросе, как поменять пределы интегрирования при замене.
В примерах я постараюсь привести такие типы замен, которые еще нигде не встречались на сайте.
Вычислить определенный интеграл
Главный вопрос здесь вовсе не в определенном интеграле, а в том, как правильно провести замену. Смотрим в таблицу интегралов и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: 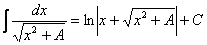
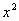
Сначала готовим наш интеграл к замене:
Из вышеуказанных соображений совершенно естественно напрашивается замена: 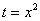
Таким образом, в знаменателе будет всё хорошо: 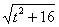
Выясняем, во что превратится оставшаяся часть 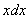
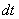
По сравнению с заменой в неопределенном интеграле у нас добавляется дополнительный этап.
Находим новые пределы интегрирования.
Это достаточно просто. Смотрим на нашу замену 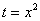
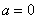
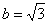
Сначала подставляем в выражение замены 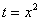
Потом подставляем в выражение замены 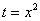
Готово. И всего-то лишь…
(1) В соответствии с заменой записываем новый интеграл с новыми пределами интегрирования.
(2) Это простейший табличный интеграл, интегрируем по таблице. Константу 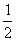
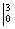
(3) Используем формулу Ньютона-Лейбница 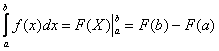
Ответ стремимся записать в максимально компактном виде, здесь я использовал свойства логарифмов.
Ещё одно отличие от неопределенного интеграла состоит в том, что, после того, как мы провели замену, никаких обратных замен проводить не надо.
А сейчас пара примеров для самостоятельного решения. Какие замены проводить – постарайтесь догадаться самостоятельно.
Вычислить определенный интеграл
Вычислить определенный интеграл
Это примеры для самостоятельного решения. Решения и ответы в конце урока.
И в заключение параграфа пара важных моментов, разбор которых появился благодаря посетителям сайта. Первый из них касается правомерности замены. В некоторых случаях её проводить нельзя! Так, Пример 6, казалось бы, разрешим с помощью универсальной тригонометрической подстановки 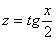
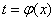
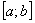
В другом электронном письме поступил следующий вопрос: «А нужно ли менять пределы интегрирования, когда мы подводим функцию под знак дифференциала?». Сначала я хотел «отмахнуться от ерунды» и автоматически ответить «конечно, нет», но затем задумался о причине появления такого вопроса и вдруг обнаружил, что информации-то не хватает. А ведь она, пусть и очевидна, но очень важнА:
Если мы подводим функцию под знак дифференциала, то менять пределы интегрирования не нужно! Почему? Потому что в этом случае нет фактического перехода к новой переменной. Например:
И здесь подведение гораздо удобнее академичной замены 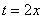
Большое спасибо за ваши письма!
Метод интегрирования по частям в определенном интеграле
Здесь новизны еще меньше. Все выкладки статьи Интегрирование по частям в неопределенном интеграле в полной мере справедливы и для определенного интеграла.
Плюсом идёт только одна деталь, в формуле интегрирования по частям добавляются пределы интегрирования:
Формулу Ньютона-Лейбница здесь необходимо применить дважды: для произведения 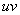
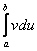
Тип интеграла для примера я опять подобрал такой, который еще нигде не встречался на сайте. Пример не самый простой, но очень и очень познавательный.
Вычислить определенный интеграл
Решаем.
Интегрируем по частям:
У кого возникли трудности с интегралом 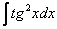
(1) Записываем решение в соответствии с формулой интегрирования по частям.
(2) Для произведения 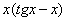
(3) Берем два оставшихся интеграла. Интеграл 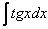
(4) Применяем формулу Ньютона-Лейбница для двух найденных первообразных.
Далее ответ доводится «до ума». Повторюсь, будьте ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫ при подстановках и заключительных вычислениях. Здесь допускают ошибки чаще всего.
Если честно, я недолюбливаю формулу 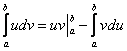
Вычислить определенный интеграл
На первом этапе я нахожу неопределенный интеграл:
Интегрируем по частям:
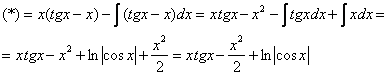
Первообразная функция найдена. Константу 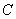
В чём преимущество такого похода? Не нужно «таскать за собой» пределы интегрирования, действительно, замучаться можно десяток раз записывать мелкие значки пределов интегрирования
На втором этапе я провожу проверку (обычно на черновике).
Тоже логично. Если я неправильно нашел первообразную функцию, то неправильно решу и определенный интеграл. Это лучше выяснить немедленно, дифференцируем ответ:
Получена исходная подынтегральная функция, значит, первообразная функция найдена верно.
Третий этап – применение формулы Ньютона-Лейбница:
И здесь есть существенная выгода! В «моём» способе решения гораздо меньший риск запутаться в подстановках и вычислениях – формула Ньютона-Лейбница применяется всего лишь один раз. Если чайник решит подобный интеграл по формуле 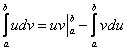
Рассмотренный алгоритм решения можно применить для любого определенного интеграла.
Уважаемый студент, распечатай и сохрани:
Что делать, если дан определенный интеграл, который кажется сложным или не сразу понятно, как его решать?
1) Сначала находим неопределенный интеграл (первообразную функцию). Если на первом же этапе случился облом, дальше рыпаться с Ньютоном и Лейбницем бессмысленно. Путь только один – повышать свой уровень знаний и навыков в решении неопределенных интегралов.
2) Проверяем найденную первообразную функцию дифференцированием. Если она найдена неверно, третий шаг будет напрасной тратой времени.
3) Используем формулу Ньютона-Лейбница. Все вычисления проводим ПРЕДЕЛЬНО ВНИМАТЕЛЬНО – тут самое слабое звено задания.
И, на закуску, интеграл для самостоятельного решения.
Вычислить определенный интеграл
Решение и ответ где-то рядом.
Следующий рекомендуемый урок по теме – Как вычислить площадь фигуры с помощью определенного интеграла? Там речь пойдет о геометрическом смысле определенного интеграла. Дополнительные материалы по определенному интегралу также можно найти в статье Эффективные методы вычисления определенных интегралов. Данный урок содержит ряд очень важных технических приёмов и позволит существенно повысить навыки вычисления определенного интеграла.
Пример 2: Решение:
Пример 4: Решение:
Пример 6: Решение:
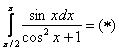
Проведем замену переменной: 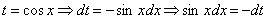
Новые переделы интегрирования: 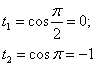
Примечания: В рассмотренном интеграле – как раз тот случай, когда уместно применить свойство определенного интеграла 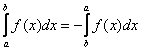
Если не совсем понятно, почему из арктангенса можно вынести минус, рекомендую обратиться к методическому материалу Графики и свойства элементарных функций.
Пример 7: Решение: 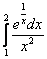
Замена: 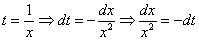
Новые пределы интегрирования: 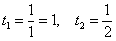
Пример 9: Решение: 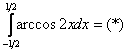
Интегрируем по частям: 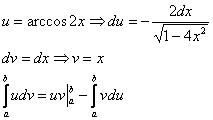
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5