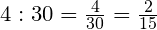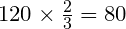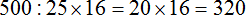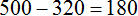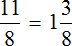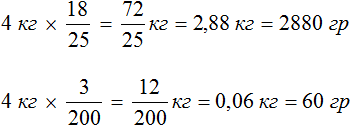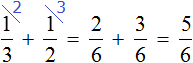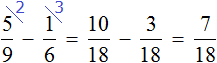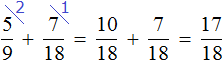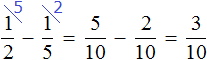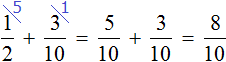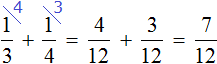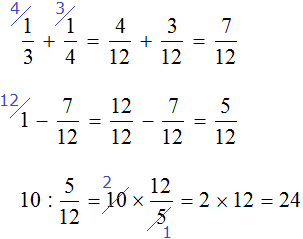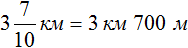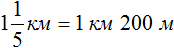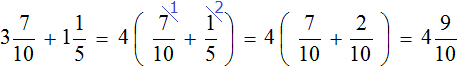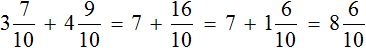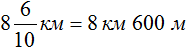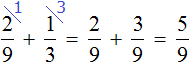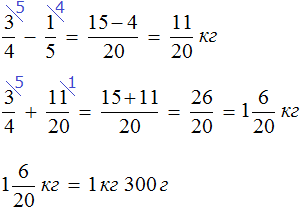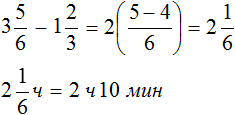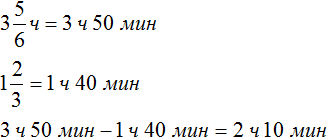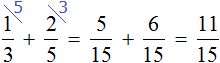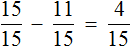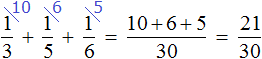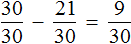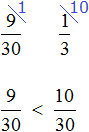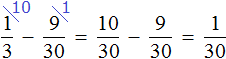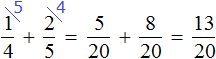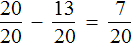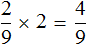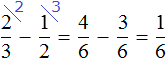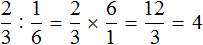Как решать задачи дробями

Задачи на дроби

Выражение части в долях целого

Чтобы выразить часть в долях целого, нужно часть разделить на целое.

Задача. В классе 30 учащихся, отсутствуют четверо. Какая часть учащихся отсутствует?

Ответ: В классе отсутствует 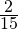учащихся.

Нахождение дроби от числа

Для решения задач, в которых требуется найти часть целого справедливо следующее правило:

Если часть целого выражена дробью, то чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на её числитель.

Задача 1. Было 600 рублей, этой суммы истратили. Сколько денег истратили?

Решение: Чтобы найти от 600 рублей, надо эту сумму разделить на 4 части, тем самым мы узнаем, сколько денег составляет одна четвёртая часть:

Ответ: Истратили 150 рублей.

Задача 2. Было 1000 рублей, этой суммы истратили. Сколько денег было истрачено?

Решение: Из условия задачи мы знаем, что 1000 рублей состоит из пяти равных частей. Сначала найдём сколько рублей составляет одна пятая часть от 1000, а затем узнаем сколько рублей составляют две пятых:

1) 1000 : 5 = 200 (р.) — одна пятая часть.

2) 200 · 2 = 400 (р.) — две пятых части.

Эти два действия можно объединить:

Ответ: Было истрачено 400 рублей.

Второй способ нахождения части целого:

Чтобы найти часть целого, можно умножить целое на дробь, выражающую эту часть целого.

Задача 3. По уставу кооператива, для правомочности отчётного собрания на нём должно присутствовать не менее членов организации. В кооперативе 120 членов. При каком составе может состояться отчётное собрание?

Ответ: Отчётное собрание может состояться при наличии 80 членов организации.

Нахождение числа по его дроби

Для решения задач, в которых требуется найти целое по его части справедливо следующее правило:

Если часть искомого целого выражена дробью, то чтобы найти это целое, можно данную часть разделить на числитель дроби и результат умножить на её знаменатель.

Задача 1. Потратили 50 рублей, это составило от первоначальной суммы. Найдите первоначальную сумму денег.

Решение: Из описания задачи мы видим, что 50 рублей в 6 раз меньше первоначальной суммы, т. е. первоначальная сумма в 6 раз больше, чем 50 рублей. Чтобы найти эту сумму, надо 50 умножить на 6:

Ответ: Первоначальная сумма — 300 рублей.

Задача 2. Потратили 600 рублей, это составило от первоначальной суммы денег. Найдите первоначальную сумму.

Решение: Будем считать, что искомое число состоит из трёх третьих долей. По условию две трети числа равны 600 рублей. Сначала найдём одну треть от первоначальной суммы, а затем сколько рублей составляют три третьих (первоначальная сумма):

Ответ: Первоначальная сумма — 900 рублей.

Второй способ нахождения целого по его части:

Чтобы найти целое по величине выражающей его часть, можно разделить эту величину на дробь, выражающую данную часть.

Задача 3. Отрезок AB, равный 42 см, составляет 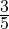длины отрезка CD. Найти длину отрезка CD.

Ответ: Длина отрезка CD 70 см.

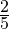
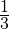
Задача 4. В магазин привезли арбузы. До обеда магазин продал , после обеда — привезённых арбузов, и осталось продать 80 арбузов. Сколько всего арбузов привезли в магазин?

Решение: Сначала узнаем, какую часть от привезённых арбузов составляет число 80. Для этого примем за единицу общее количество привезённых арбузов и вычтем из неё то количество арбузов, которое получилось реализовать (продать):

Итак, мы узнали, что 80 арбузов составляет от общего количества привезённых арбузов. Теперь узнаем сколько арбузов от общего количества составляет , а затем сколько арбузов составляют (количество привезённых арбузов):

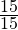
2) 80 : 4 · 15 = 300 (арбузов).

Ответ: Всего в магазин привезли 300 арбузов.

Источник

Репетитор по математике о задачах на дроби в 5-6 классе

Задачи на части (на дроби) в 5 — 6 классе, безусловно, тяжелейшая тема для преподавания. Возможно даже самая тяжелая за весь школьный курс. Как может построить свою работу с ней репетитор по математике? Рассмотрим некоторые приемы обучения решению таких задач, опишем связанные с темой проблемы и поговорим о ее дидактике.

Причиной большинства обращений к репетитору в 5 классе является повальное непонимание законов разделения на части. Это естественно, ибо задачи, на которых формируется представление о долях, предъявляют достаточно высокие (для этого возраста) требования к уровню развития ученика, часто связанные с его физиологией. Этот обстоятельство часто не позволяет репетитору математики действовать стандартно, опираясь на традиционые объяснения.

Несмотря на влияние физиогогии родители ребенка обычно стараются повлиять на ситуацию как можно быстрее. Большинству из них нужен репетитор по математике для скорейшего исправления текущей отметки. Иногда это мешает планомерно и неспешно объяснять математические законы и выстраивать темы в логически правильном порядке.

Долгое время я не решался написать об этих задачах. И дело не только в сложности восприятия материала школьниками. В изучении темы выделяется несколько этапов с различными ограничениями в использовании чисел. Не случайно дроби проходят не один год. Программа 5 класса переплетается с программой 6-го класса (а по Петерсону еще и с четвертым). Поэтому даже при одном и том же характере работы преподавателя с дробями разница в индивидуальных особенностях учеников и программах не позволяют описать методы работы репетитора по математике с темой точно и коротко. Более того, в разных учебниках «доли» изучаются в разное время, по-разному «обкладываются» задачами и по-разному интегрируются в дидактику смежных тем. Поэтому очень сложно охватить все проблемы. Надеюсь, что репетиторы по математике со стажем меня понимают.

Много раз я сталкивался с проблемами задач на дроби и уяснил для себя главное: тема требуют постепенного и долгого изучения. Ее нельзя проработать за один-два урока. Поэтому первое, что я делаю, — объясняю родителям ситуацию и прошу предоставить дополнительные часы для занятий. Не менее двух раз в неделю. Для репетитора по математике это стандартный график, позволяющий в большинстве случаев полноценно заниматься пробелами.

Репетитор по математике о своей методике

Формально мой подход не отличается от того, что предлагают другие репетиторы, а именно — решение задач в большом количестве. Однако к ним еще нужно поготовить ученика, предложить ему некий план или даже алгоритм подбора пути решения. К сожалению, его точность и прозрачность не всегда соответствует желаемому. Репетитор по математике должен понимать, какие задачи и с каким учеником следует разбирать, в каком порядке и в каком количестве. Подходы разных преподавателей могут отличаться порядком разбора задач, пояснениями, терминологией, сопровождениями в рисунках, схемах и даже их полным отсутствием. Я использую собственную базу типовых примеров и наводящих вопросов, систему записей, оформлений и обозначений (немного схожую с Петерсоновской). Оптимизирую краткие записи к задачам, делаю их удобными, информативными и ориентированными на поиск решения.

Разбор элементарных задач

Первый этап работы репетитора — знакомство ученика с базовыми задачами, обучение составлению для них кратких записей. Очень важно вложить в ученика мысль о том, что сложная задача на дроби состоит из нескольких упакованных в нее простых, с определенной последовательных элементарных операций. Их выделением и проработкой репетитор по математике занимается на первом уроке.

Выделяется 3 типа простейших задач на дроби:
1) Целая величина известна
2) Целая величина неизвестна
3) Неизвестна дробь

Для каждой из них подбирается реальная ситуация, которую удобно моделировать рисунком. Распространены примеры деления яблока или плошади. Например: Яблоко имеет массу 160 грамм, найдите вес яблока. Пример стандартный, но подходит не всех ученикам, ибо для проверки правильности демонстрируемых репетитором ариметических действий приходится делить то, что нельзя взять в руки, именно вес. При низком интеллектуальном уровене развития ученика репетитор по математике оказывается бессильным что-либо ему объяснить, ибо проблемы уходят далеко от темы «дроби». Если такое происходит, я использую пример с полом:

Пол выложен одинаковыми плитками как показано на рисунке. На каждую плитку положили по шарику. Сколько шариков лежит на пола?
Преимущество этого примера в том, что ребенок может не только выделить (закрасить) 5/8 пола, но и пересчитать количество шариков непосредственно. При этом репетитор по математике указывает на возможность ответить на вопрос через простые арифметические действия (на рядах и колонках).

Наводящие вопросы репетитора по математике

Cлабого ребенку можно еще и полдвести к выполнению действий. Для этого репетитор по математике задает ему систему наводящих вопросов, например:

Главное преимущество задачи на плитки и шарики состоит в использовании арифметических действий, каждое из которых удается проверить простым пересчетом. После того, как репетитор по математике убедился в понимании действий, он диктует ученику проверенное правило: «делим на знаменатель и умножаем на числитель».

Несмотря на то, что можно пересчитывать количество не шариков, а самих плиток, я намеренно оставляю шары в сюжете задачи. Почему? На их примере изучается ситуация, когда какой-нибудь целый объект удерживает внутри себя (или на себе) мелкие объекты (в нашем случае пол удерживает шарики). Это широко распространено в дидактике математики 5-6 класса. Часто что-то куда-то засыпается, заливается, вкладывается и равномерно распределяется по объекту. В мешки засыпают сахар, в бидоны заливают молоко и т.д. Репетитор по математике на примере шариков помогает ребенку быстрее разобраться в числовых особеннностях этих ситуаций и понять законы измерения частей объектов.

Репетитору по математике важно остановиться на терминологии и оформлении краткой записи.От того, насколько как она будет зависит идентификация правил. Ученик должен усвоить, что целый объект — это такая же величина, как и его часть, измеряемая двумя единицами: привычной (метрами, сантиметрами, килограммами, литрами, страницами, деревьями, шариками и т.д.) и «особой». В роли последней выступает целая величина. Рядом с ней в кратких записях можно поставить 1ед. Все участники элементарной задачи получают названия. То, от чего ищется часть называется целой величиной, сама дробь так и остается дробью, а часть, которую находят от целого репетитор по математике называет «частью» или «значением» дроби». Я предпочитаю второй вариант.

Задача 2-го типа: целая величина неизвестна.
(г) — вес яблока.
Чтобы найти целую величину нужно значение дроби разделеить на числитель и умножить на знаменатель.

В третьей задаче для 5 класса репетитором по математике должны быть выбраны другие числа, ибо сократить дробь пятиклашки еще не могут. Обратите внимание на то, что обыгрывается один и тот же комплект чисел. В первой задаче репетитор по математике находит целого яблока, а во второй выполняет обратные действия: по той же дроби и найденному ранее значению 100 восстановливает число 160 (его даже можно в определенный помент стереть ластиком). Прием обратных действий полезен для работы с невнимательными школьниками. Он позволяет быстро сконцентрироваться на правилах, а не на изучении нового условия новой задачи. Более того, при заранее изветном ответе ребенок убеждается в правильности выбора этих действий. Действительно, как можно в них усомниться, если репетитор по математике получает в ответе то, что и должно получиться?

Под каждой краткой записью оформляется решение и записывается правило:

1) чтобы найти значение дроби, нужно целую величину разделить на знаменатель и умножить на числитель.
2) Чтобы найти целую величну нужно разделить на числитель и умножить на знаменатель.
3) Чтобы найти дробь нужно разделить ее значение на целую величину.

Как репетитор математики работает с комбинированными задачами

Чаще всего они встречаются в 6 классе, хотя в учебнике Петерсона сочетания двух и даже трех типов задач предлагаются уже в 5 классе. Прежде всего ученик должен знать с чего начинать исследование задачи. Важно отработать каждый его этап в отдельности.

Краткая запись

Краткая запись к задаче — важнейший и незаменимый элемент методики любого хорошего репетитора по математике. Она является одновременно и опорой и средством заставить ученика перечитывать условие как минимум — два три раза. Правильно составленная краткая запись в сочетании с четкими правилами «трех типов» позволяют разложить комбинированную задачу на несколько элементарных. Поэтому репетитору чрезвычайно важно научить правильно ее составлять.

Как репетитор по математике работает с текстами?
Главной проблемой составления краткой записи является проблема анализа текста задачи. Практика показывает, что дети крайне невнимательно и низкоэффективно с ним работают. Не умеют выделять ценную информацию о величинах и сами величины, сортировать главное и второстепенное. Для борьбы с такими проблемами репетитор математики может взять на вооружение метод слежения. Что такое краткая запись? — всего лишь короткий текст условия, из которого выброшены лишние слова, а названия величин и их значения записаны отдельными строками. Что мешает репетитору по математике выделять эти слова в тексте? Особенно важно научить поиску целых величин, на которые в краткой записи будут указывать стрелки. Репетитор должен обратить внимание ученика на то, что слово или фраза, написанная сразу после дроби, указывает на единицу измерения дроби, то есть на ее целую величину. Репетитору по математике никто не запрещает выделить ее в тексте (подчеркнуть или записать другим цветом) и поставить к ней стрелочку. Пример оформления:

Если внимание ребенка ослаблено, на первых порах ему лучше предлагать уже размеченные тексты, с выделенными целыми величинами и стрелочками.

Для того, чтобы не пропустить ни одну из участвующих величин репетитору по математике нужно задать вопрос: Что в задаче можно измерить? Пок ученик думато, репетитор подчеркивает в тексте соответствующие им слова. В нашем случае это показано синим цветом.

Например, краткая запись к задаче про вишню может быть следующей:

Попрбуйте составить краткую запись к олимпиадной задачке: мама испекла булочки. Аня съеха 2/3 всех булочек и еще 2. Петр съел 2/3 остатка и еще 2 булочки, а Денис съел 2/3 последнего остатки и последние 2 булочки. Сколько булочек испекла мама?

Александр Николаевич, репетитор по математике Москва (м.Щукинская, Строгино)

Источник

Задачи на дроби

Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на дроби.

Прежде чем решать задачи на дроби, необходимо досконально изучить все темы, касающиеся дробей. Ниже приведен список уроков, которые можно повторить.

Каждая задача, приведенная в данном уроке, относится к категории элементарных. Если какая-то задача непонятна, это указывает на то, что предыдущий материал усвоен недостаточно хорошо.

Задачи на дроби

Задача 1. В классе школьников составляют отличники. Какую часть составляют остальные? Сделать графическое описание задачи. Рисунок может быть любым.

Решение

Если составляют отличники, то составляют остальные

Задача 2. В классе школьников составляют отличники, составляют хорошисты, составляют троечники. Сделать графическое описание задачи. Рисунок может быть любым.

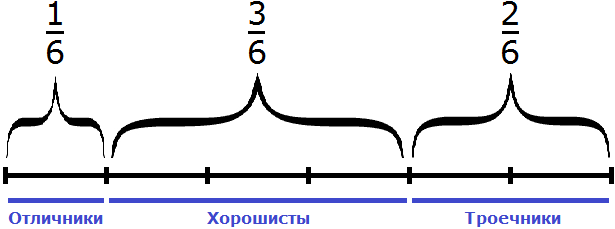
Задача 3. В классе 24 школьника. школьников составляют отличники, составляют хорошисты, составляют троечники. Сколько в классе отличников, хорошистов и троечников?

Решение

24 : 6 × 1 = 4 × 1 = 4 (отличника)

24 : 6 × 3 = 4 × 3 = 12 (хорошистов)

24 : 6 × 2 = 4 × 2 = 8 (троечников)

Проверка

4 + 12 + 8 = 24 (школьника)

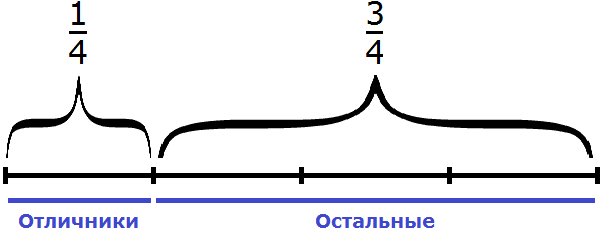
Задача 4. В классе школьников составляют отличники, составляют хорошисты. Какую часть составляют троечники?

Решение

Школьники разделены на 6 частей. На одну из частей приходятся отличники, на три части — хорошисты. Нетрудно догадаться, что на остальные две части приходятся троечники. Значит школьников составляют троечники

Не приводя рисунков можно сложить дроби и , и полученный результат вычесть из дроби , которая выражает всю часть школьников. Другими словами, сложить отличников и хорошистов, затем вычесть этих отличников и хорошистов из общего количества школьников

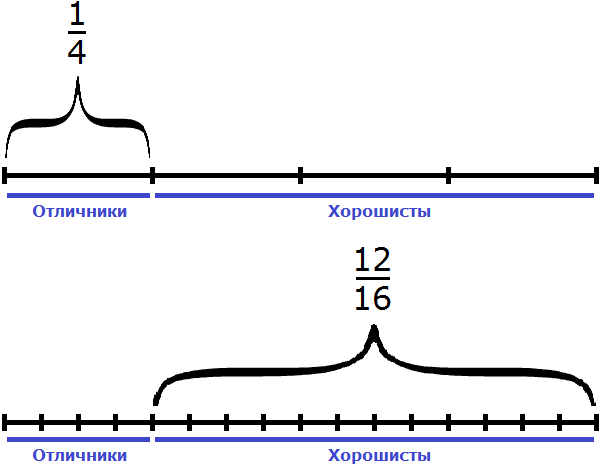
Задача 5. В классе 16 школьников. Из них составляют отличники, составляют хорошисты. Сколько отличников и хорошистов в классе? Сделать графическое описание задачи. Рисунок может быть любым.

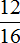
Решение

16 : 4 × 1 = 4 × 1 = 4 (отличника)

16 : 16 × 12 = 1 × 12 = 12 (хорошистов)

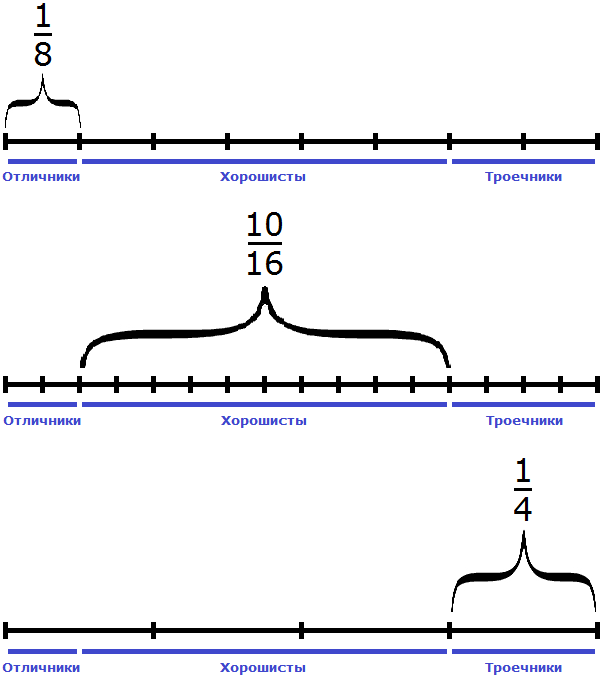
Задача 6. В классе 16 школьников. Из них составляют отличники, составляют хорошисты, составляют троечники. Сколько отличников, хорошистов и троечников в классе? Сделать графическое описание задачи. Рисунок может быть любым.

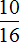
Решение

16 : 8 × 1 = 2 × 1 = 2 (отличника)

16 : 16 × 10 = 1 × 10 = 10 (хорошистов)

16 : 4 = 4 (троечника)

Задача 7. Из зерен пшеницы производят полтавскую крупу, масса которой составляет 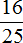массы зерна пшеницы, а остальное составляют кормовые отходы. Сколько можно получить полтавской крупы и кормовых отходов из 500 центнеров пшеницы

Решение

Найдем 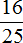от 500 центнеров:

Теперь найдем массу кормовых отходов. Для этого вычтем из 500 ц массу полтавской крупы:

Значит из 500 центнеров зерен пшеницы можно получить 320 центнеров полтавской крупы и 180 центнеров кормовых отходов.

Задача 8. Килограмм сахара стоит 88 рублей. Сколько стоит кг сахара? кг? кг? кг?

Решение

1) кг это половина одного килограмма. Если один килограмм стоит 88 рублей, то половина килограмма будет стоит половину от 88, то есть 44 рубля. Если найти половину от 88 рублей, мы получим 44 рубля

2) кг это четверть килограмма. Если один килограмм стоит 88 рублей, то четверть килограмма будет стоит четверти от 88 рублей, то есть 22 рубля. Если найти от 88 рублей, мы получим 22 рубля

3) Дробь означает, что килограмм разделен на восемь частей, и оттуда взято три части. Если один килограмм стоит 88 рублей, то стоимость трех восьми килограмм будут стоить от 88 рублей. Если найти от 88 рублей, мы получим 33 рубля.

4) Дробь означает, что килограмм разделен на восемь частей, и оттуда взято одиннадцать частей. Но невозможно взять одиннадцать частей, если их только восемь. Мы имеем дело с неправильной дробью. Сначала выделим в ней целую часть:

Одиннадцать восьмых это один целый килограмм и килограмма. Теперь мы можем по отдельности найти стоимость одного целого килограмма и стоимость трёх восьмых килограммов. Один килограмм, как было указано выше стоит 88 рублей. Стоимость кг мы также находили и получили 33 рубля. Значит кг сахара будет стоит 88+33 рубля, то есть 121 рубль.

Стоимость можно найти не выделяя целой части. Для этого достаточно найти от 88.

Но выделив целую часть можно хорошо понять, как сформировалась цена на кг сахара.

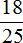
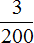
Задача 9. Финики содержат сахара и минеральных солей. Сколько граммов каждого из веществ содержится в 4 кг фиников?

Решение

Узнаем сколько граммов сахара содержится в одном килограмме фиников. Один килограмм это тысяча грамм. Найдем 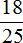от 1000 грамм:

В одном килограмме фиников содержится 720 грамм сахара. Чтобы узнать сколько грамм сахара содержится в четырех килограммах, нужно 720 умножить на 4

Теперь узнаем сколько минеральных солей содержится в 4 килограммах фиников. Но сначала узнаем сколько минеральных солей содержится в одном килограмме. Один килограмм это тысяча грамм. Найдем 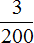от 1000 грамм:

В одном килограмме фиников содержится 15 грамм минеральных солей. Чтобы узнать сколько грамм минеральных солей содержится в четырех килограммах, нужно 15 умножить на 4

Значит в 4 кг фиников содержится 2880 грамм сахара и 60 грамм минеральных солей.

Решение для данной задачи можно записать значительно короче, двумя выражениями:

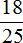
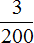
Суть в том, что от 4 килограмм нашли и полученные 2,88 перевели в граммы, умножив на 1000. Тоже самое сделали и для минеральных солей — от 4 кг нашли и получившиеся килограммы перевели в граммы, умножив на 1000. Обратите также внимание на то, что дробь от числа найдена упрощенным способом — прямым умножением числа на дробь.

Задача 10. Поезд прошел 840 км, что составляет его пути. Какое расстояние ему осталось пройти? Каково расстояние всего пути?

Решение

В задаче говорится, что 840 км это от его пути. Знаменатель дроби указывает на то, что весь путь разделен на семь равных частей, а числитель указывает на то, что четыре части этого пути уже пройдено и составляют 840 км. Поэтому, разделив 840 км на 4, мы узнаем сколько километров приходится на одну часть:

А поскольку весь путь состоит из семи частей, то расстояние всего пути можно найти, умножив 210 на 7:

Теперь ответим на второй вопрос задачи — какое расстояние осталось пройти поезду? Если длина пути 1470 км, а пройдено 840, то оставшийся путь равен 1470−840, то есть 630

Задача 11. Одна из групп, покорившая горную вершину Эверест, состояла из спортсменов, проводников и носильщиков. Спортсменов в группе было 25, число проводников составляло числа спортсменов, а число спортсменов и проводников вместе лишь 9/140 числа носильщиков. Сколько было носильщиков в этой экспедиции?

Решение

Спортсменов группе 25. Проводников составляет числа спортсменов. Найдем от 25 и узнаем сколько в группе проводников:

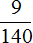
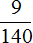
Спортсменов и проводников вместе — 45 человек. Это число составляет от числа носильщиков. Зная что от числа носильщиков это 45 человек, мы можем найти общее число носильщиков. Для этого найдем число по дроби:

45 : 9 × 140 = 5 × 140 = 700

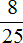
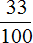
Задача 12. В школу привезли 900 новых учебников, из них учебники по математике составляли всех книг, учебники по русскому языку всех книг, а остальные книги были по литературе. Сколько привезли книг по литературе

Узнаем сколько составляют учебники по математике:

900 : 25 × 8 = 288 (книг по математике)

Узнаем сколько учебников по русскому языку:

900 : 100 × 33 = 297 (книг по русскому языку)

Узнаем сколько учебников по литературе. Для этого из общего числа книг вычтем учебники по математике и по русскому:

900 – (288+297) = 900 – 585 = 315

Проверка

288 + 297 + 315 = 900

Задача 13. В первый день продали , а во второй день поступившего в магазин винограда. Какую часть винограда продали за два дня?

Решение

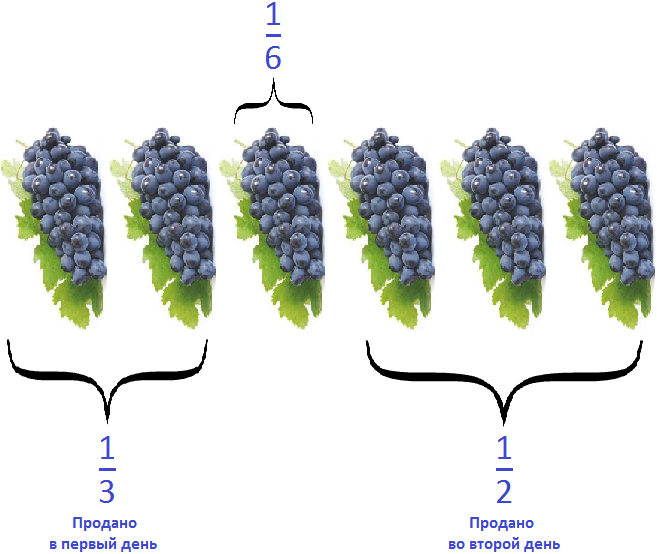
За два дня продали винограда. Эта часть получается путем сложения дробей и

Можно представить поступивший в магазин виноград в виде шести гроздей. Тогда винограда это две грозди, винограда — три грозди, а винограда это пять гроздей из шести, проданные за два дня. Ну и нетрудно увидеть, что осталась одна гроздь, выраженная дробь (одна гроздь из шести)

Задача 14. Вера в первый день прочитала книги, а во второй день на меньше. Какую часть книги прочитала Вера во второй день? Успела ли она прочитать книгу за два дня?

Решение

Определим часть книги, прочитанной во второй день. Сказано, что во второй день прочитано на меньше, чем в первый день. Поэтому из нужно вычесть

Во второй день Вера прочитала 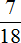книги. Теперь ответим на второй вопрос задачи — успела ли Вера прочитать книгу за два дня? Сложим то, что Вера прочитала в первый и во второй день:

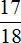
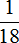
За два дня Вера прочитала книги, но осталось ещё книги. Значит Вера не успела прочитать всю книгу за два дня.

Сделаем проверку. Предположим что книга, которую читала Вера, имела 180 страниц. В первый день она прочла книги. Найдем от 180 страниц

180 : 9 × 5 = 100 (страниц)

Во второй день Вера прочитала на меньше, чем в первый. Найдем от 180 страниц, и вычтем полученный результат из 100 листов, прочитанных в первый день

180 : 6 × 1 = 30 × 1 = 30 (страниц)

100 − 30 = 70 (страниц во второй день)

Проверим, являются ли 70 страниц 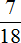частью книги:

180 : 18 × 7 = 10 × 7 = 70 (страниц)

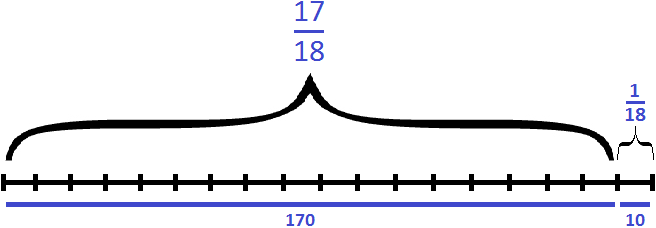
Теперь ответим на второй вопрос задачи — успела ли Вера прочитать все 180 страниц за два дня. Ответ — не успела, поскольку за два дня она прочла только 170 страниц

100 + 70 = 170 (страниц)

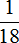
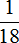
Осталось прочесть еще 10 страниц. В задаче в роли остатка у нас была дробь . Проверим являются ли 10 страниц частью книги?

180 : 18 × 1 = 10 × 1 = 10 (страниц)

Задача 15. В одном пакете кг, а в другом на кг меньше. Сколько килограммов конфет в двух пакетах вместе?

Решение

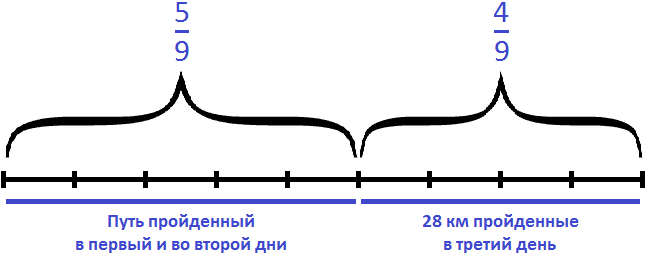
Определим массу второго пакета. Она на кг меньше, чем масса первого пакета. Поэтому из массы первого пакета вычтем массу второго:

Масса второго пакета 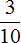кг. Определим массу обоих пакетов. Сложим массу первого и массу второго:

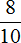
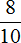
Масса обоих пакетов кг. А килограмма это 800 граммов. Можно решать такую задачу, работая с дробями, складывая и вычитая их. Также можно сначала найти число по данным в задаче дробям и приступить к решению. Так килограмма это 500 граммов, а кг это 200 граммов

1000 : 2 × 1 = 500 × 1 = 500 г

1000 : 5 × 1 = 200 × 1 = 200 г

Во втором пакете на 200 граммов меньше, поэтому чтобы определить массу второго пакета, нужно из 500 г вычесть 200 г

Ну и напоследок сложить массы обоих пакетов:

Задача 16. Туристы прошли путь от турбазы до озера за 4 дня. В первый день они прошли всего пути, во второй оставшегося пути, а в третий и четвертый дни проходили по 12 км. Чему равна длина всего пути от турбазы до озера?

Решение

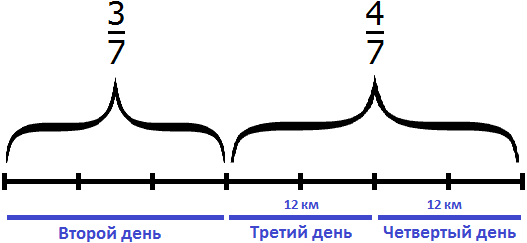
В третий и четвертый день туристы прошли 24 км и это составляет от пути, пройденного во второй, третий и четвертый дни. Зная, что составляют 24 км, мы можем найти весь путь, пройденный во второй, третий и четвертый день:

24 : 4 × 7 = 6 × 7 = 42 км

Во второй, третий и четвертый день туристы прошли 42 км. Теперь найдем от этого пути. Так мы узнаем сколько километров туристы прошли во второй день:

42 : 7 × 3 = 6 × 3 = 18 км

Теперь возвращаемся к началу задачи. Сказано, что в первый день туристы прошли всего пути. Весь путь разделен на четыре части, и на первую часть приходится путь, пройденный в первый день. А путь, который приходится на остальные три части, мы уже нашли — это 42 километра, пройденные во второй, третий и четвертый дни. Нарисуем наглядную схему, иллюстрирующую первый и остальные три дня:

Зная, что пути составляют 42 километра, мы можем найти длину всего пути:

Значит длина пути от турбазы до озера составляет 56 километров. Сделаем проверку. Для этого сложим все пути, пройденные туристами в каждый из четырех дней.

Сначала найдем путь пройденный в первый день:

56 : 4 × 1 = 14 (в первый день)

14 + 18 + 12 + 12 = 56

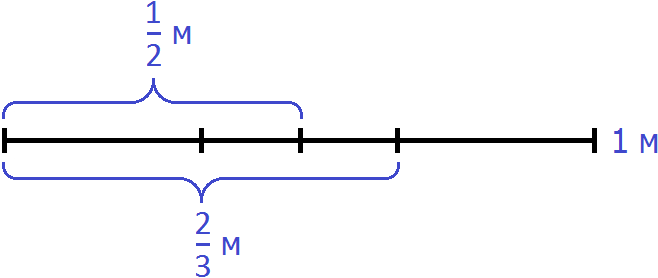
Задача из арифметики известного среднеазиатского математика Мухаммеда ибн-Мусы ал-Хорезми (IX век н. э.)

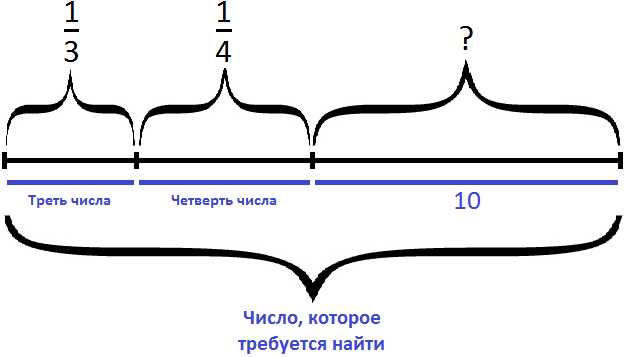
«Найти число, зная, что если отнять от него одну треть и одну четверть, то получится 10»

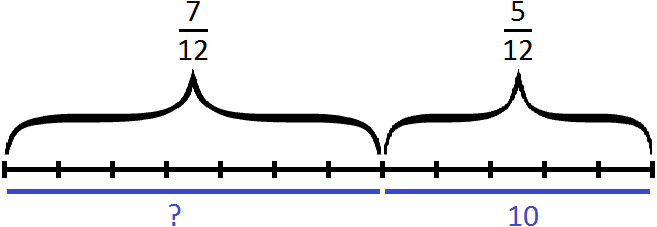
Изобразим число, которое мы хотим найти, в виде отрезка, разделенного на три части. В первой части отрезка отметим треть, во второй — четверть, оставшаяся третья часть будет изображать число 10.

Сложим треть и четверть:

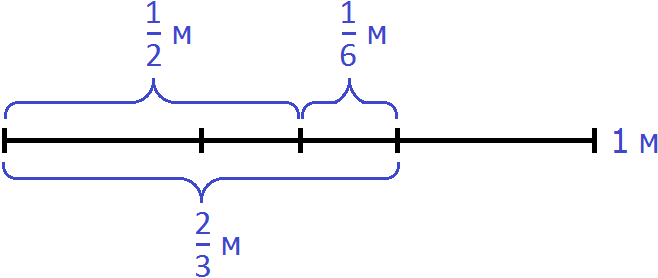
Теперь изобразим отрезок, разделенный на 12 частей. Отметим на нем дробь 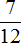, остальные пять частей пойдут на число 10:

Зная, что пять двенадцатых числа составляют число 10, мы можем найти всё число:

10 : 5 × 12 = 2 × 12 = 24

Мы нашли всё число — оно равно 24.

Эту задачу можно решить не приводя рисунков. Для этого, сначала нужно сложить треть и четверть. Затем из единицы, которая играет роль неизвестного числа, вычесть результат сложения трети и четверти. Затем по полученной дроби определить всё число:

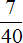
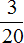
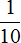
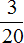
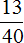
Задача 17. Семья, состоящая из четырех человек, в месяц зарабатывает 80 тысяч рублей. Бюджет распланирован следующим образом: на еду, на коммунальные услуги, на Интернет и ТВ, на лечение и походы по врачам, на пожертвование в детский дом, на проживание в съемной квартире, в копилку. Сколько денег выделено на еду, коммунальные услуги, на Интернет и ТВ, на лечение и походы по врачам, пожертвование на детский дом, на проживание в съемной квартире, и на копилку?

Решение

80 : 40 × 7 = 14 (тыс. на еду)

80 : 20 × 1 = 4 × 1 = 4 тыс. (на коммунальные услуги)

80 : 20 × 1 = 4 × 1 = 4 тыс. (на Интернет и ТВ)

80 : 20 × 3 = 4 × 3 = 12 тыс. (на лечение и походы по врачам)

80 : 10 × 1 = 8 × 1 = 8 тыс. (на пожертвование в детский дом)

80 : 20 × 3 = 4 × 3 = 12 тыс. (на проживание в съемной квартире)

80 : 40 × 13 = 2 × 13 = 26 тыс. (в копилку)

Проверка

14 + 4 + 4 + 12 + 8 + 12 + 26 = 80

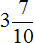
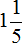
Задача 18. Туристы во время похода за первый час прошли км, а за второй на км больше. Сколько километров прошли туристы за два часа?

Решение

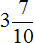
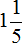
Найдем числа по дробям. это три целых километра и семь десятых километра, а семь десятых километра это 700 метров:

это один целый километр и одна пятая километра, а одна пятая километра это 200 метров

Определим длину пути, пройденного туристами за второй час. Для этого к 3 км 700 м нужно прибавить 1 км 200 м

3 км 700 м + 1 км 200 м = 3700м + 1200м = 4900м = 4 км 900 м

Определим длину пути, пройденного туристами за два часа:

3 км 700 м + 4 км 900 = 3700м + 4900м = 8600м = 8 км 600 м

Значит за два часа туристы прошли 8 километров и еще 600 метров. Решим эту задачу с помощью дробей. Так её можно значительно укоротить

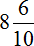
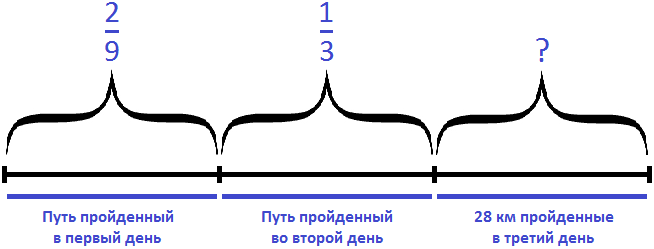
Получили ответ километра. Это восемь целых километров и шесть десятых километра, а шесть десятых километра это шестьсот метров

Задача 19. Геологи прошли долину, расположенную между горами, за три дня. В первый день они прошли , во второй всего пути и в третий оставшиеся 28 км. Вычислить длину пути, проходящего по долине.

Решение

Изобразим путь в виде отрезка, разделенного на три части. В первой части отметим пути, во второй части пути, в третьей части оставшиеся 28 километров:

Сложим части пути, пройденные в первый и во второй день:

За первый и второй дни геологи прошли всего пути. На остальные пути приходятся 28 километров, пройденные геологами в третий день. Зная, что 28 километров это всего пути, мы можем найти длину пути, проходящего по долине:

28 : 4 × 9 = 7 × 9 = 63 км

Проверка

63 : 9 × 5 = 7 × 5 = 35

63 : 9 × 4 = 7 × 4 = 28

Задача 20. Для приготовления крема использовали сливки, сметану и сахарную пудру. Сметану и сливки составляют 844,76 кг, а сахарная пудра и сливки 739,1 кг. Сколько в отдельности сливок, сметаны и сахарной пудры содержится в 1020,85 кг крема?

Решение

сметана и сливки — 844,76 кг
сахарная пудра и сливки — 739,1 кг

Вытащим из 1020,85 кг крема сметану и сливки (844,76 кг). Так мы найдем массу сахарной пудры:

1020,85 кг — 844,76 кг = 176,09 (кг сахарной пудры)

Вытащим из сахарной пудры и сливок сахарную пудру (176,09 кг). Так мы найдем массу сливок:

739,1 кг — 176,09 кг = 563,01 (кг сливок)

Вытащим сливки из сметаны и сливок. Так мы найдем массу сметаны:

844,76 кг — 563,01 кг = 281,75 (кг сметаны)

176,09 (кг сахарная пудра)

Проверка

176,09 кг + 563,01 кг + 281,75 кг = 1020,85 кг

1020,85 кг = 1020,85 кг

Задача 21. Масса бидона, заполненного молоком равна 34 кг. Масса бидона, заполненного наполовину, равна 17,75 кг. Какова масса пустого бидона?

Решение

Вычтем из массы бидона, заполненного молоком, массу бидона заполненного наполовину. Так мы получим массу содержимого бидона, заполненного наполовину, но уже без учета массы бидона:

34 кг − 17,75 кг = 16,25 кг

16,25 это масса содержимого бидона заполненного наполовину. Умножим эту массу на 2, получим массу бидона заполненного полностью:

16,25 кг × 2 = 32,5 кг

32,5 кг это масса содержимого бидона. Чтобы вычислить массу пустого бидона, нужно из 34 кг вычесть массу его содержимого, то есть 32,5 кг

34 кг − 32,5 кг = 1,5 кг

Ответ: масса пустого бидона составляет 1,5 кг.

Задача 22. Сливки составляют 0,1 массы молока, а сливочное масло составляет 0,3 массы сливок. Сколько сливочного масла можно получить из суточного надоя коровы, равного 15 кг молока?

Решение

Определим сколько килограмм сливок можно получить с 15 кг молока. Для этого найдем 0,1 часть от 15 кг.

15 × 0,1 = 1,5 (кг сливок)

Теперь определим сколько сливочного масла можно получить с 1,5 кг сливок. Для этого найдем 0,3 часть от 1,5 кг

1,5 кг × 0,3 = 0,45 (кг сливочного масла)

Ответ: из 15 кг молока можно получить 0,45 кг сливочного масла.

Задача 23. 100 кг клея для линолеума содержат 55 кг асфальта, 15 кг канифоли, 5 кг олифы и 25 кг бензина. Какую часть этого клея образует каждая из его составляющих?

Решение

Представим, что 100 кг клея как 100 частей. Тогда на 55 частей приходится асфальт, на 15 частей — канифоль, на 5 частей — олифа, на 25 частей — бензин. Запишем эти части в виде дробей, и по возможности сократим получающиеся дроби:

Ответ: 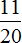клея составляет асфальт, составляет канифоль, составляет олифа, составляет бензин.

Задачи для самостоятельного решения

Решение

Ответ: масса двух пакетов вместе составляет 1 кг 300 г

Решение

Второй способ

Ответ: театральное представление длилось 2 часа 10 минут.

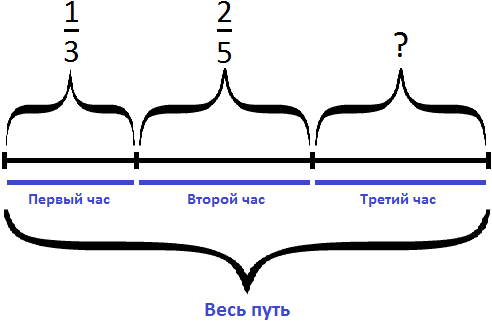
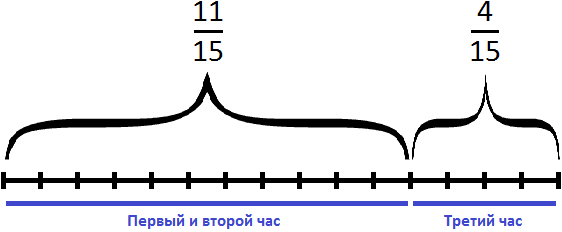
Решение

Определим часть пути, пройденного лыжником за два часа движения. Для этого сложим дроби, выражающие пути пройденные за первый и второй час:

Определим часть пути, пройденного лыжником за третий час. Для этого из всех частей вычтем часть пути, пройденного за первый и второй час движения:

Ответ: в третий час лыжник прошел всего расстояния.

Решение

Определим часть школьников, которые участвовали в футболе, баскетболе и в прыжках:

Определим часть школьников, которые участвовали в беге:

Узнаем на какую часть бегунов больше (или меньше) чем футболистов. Для начала сравним дроби 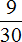и

Требовалось узнать на какую часть бегунов больше (или меньше) чем футболистов. Мы выяснили, что бегунов меньше, чем футболистов. Выясним на какую часть их меньше:

Бегунов меньше, чем футболистов на часть.

Теперь узнаем на какую часть бегунов больше (или меньше) чем баскетболистов. Для начала сравним дроби 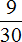и

Требовалось узнать на какую часть бегунов больше (или меньше) чем баскетболистов. Мы выяснили, что бегунов больше, чем баскетболистов. Выясним на какую часть их больше:

Бегунов больше, чем баскетболистов на часть.

Ответ: бегунов было на часть меньше, чем футболистов и на часть больше, чем баскетболистов.

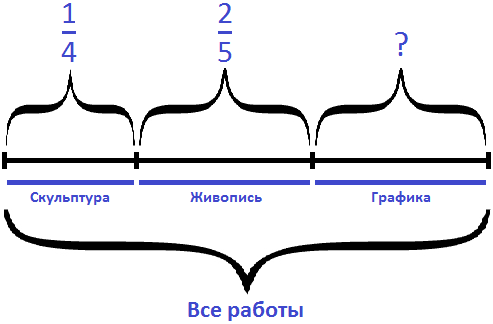
Задача 5. На выставке художественных работ представлена живопись, скульптура и графика. всех работ составляет скульптура, – живопись, оставшуюся часть – графика. Какую часть всех работ составляет графика?

Решение

Сложим дроби, выражающие скульптуру и живопись:

Определим какую часть всех работ составляет графика:

Ответ: 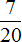всех работ составляет графика.

Задача 6. Рабочие отремонтировали дорогу длиной 820 м за три дня. Во вторник они отремонтировали этой дороги, а в среду оставшейся части. Сколько метров дороги отремонтировали рабочие в четверг?

Решение

Определим длину дороги, отремонтированной во вторник:

Определим длину дороги, отремонтированной в среду. Известно, что в этот день рабочие отремонтировали оставшейся дороги. Оставшаяся дорога это 820−328, то есть 492

Определим длину дороги, отремонтированной в четверг. Для этого вычтем из 820 длины дорог, отремонтированных во вторник и в среду:

820 − (328 + 328) = 820 − 656 = 164 м

Ответ: в четверг рабочие отремонтировали 164 метра дороги.

Задача 7. В книге три рассказа. Наташа прочла первый рассказ за ч, на чтение второго рассказа она потратила на ч больше, а чтение третьего рассказа заняло на ч меньше, чем чтение первого и второго рассказов вместе. Сколько времени ушло у Наташи на чтение всей книги?

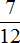
Решение

Определим время за которое Наташа прочитала первый рассказ. Она прочила его за треть часа. Треть часа это 20 минут

60 : 3 × 1 = 20 минут

Определим время за которое Наташа прочитала второй рассказ. Она прочила его на ч больше. часа это 10 минут. Прибавим к 20 минутам 10 минут, получим время чтения второго рассказа:

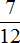
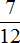
Определим время за которое Наташа прочитала третий рассказ. Она прочитала его на ч меньше, чем чтение первого и второго рассказов вместе. часа это 35 минут. Вычтем 35 из времени, затраченного на чтение первого и второго рассказа вместе (50 м)

Определим сколько времени ушло у Наташи на чтение всей книги:

20 + 30 + 15 = 65 минут = 1 ч 5 минут

На чтение всей книги у Наташи ушел 1 час и 5 минут. Решим эту задачу с помощью дробей. Так ее можно значительно укоротить:

это один целый час и часа, а одну двенадцатую часа составляют 5 минут.

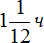
Ответ: на чтение всей книги у Наташи ушло

Задача 8. Из одной тонны хлопка-сырца можно изготовить 3400 м ткани, 1,05 ц пищевого масла и 0,225 т жмыха. Сколько метров ткани, пищевого масла и жмыха можно получить из 32,4 ц хлопка-сырца?

Решение

Переведем 32,4 ц в тонны. Одна тонна составляет 10 центнеров. Чтобы узнать сколько таких десять центнеров (имеется ввиду тонн) в 32,4 центнерах, нужно 32,4 разделить на 10

Определим сколько метров ткани можно получить с 3,24 тонн хлопка-сырца. С одной тонны, как указано в задаче, получается 3400 метров ткани. А с 3,24 тонн будет получено в 3,24 раза больше ткани

3400 × 3,24 = 11016 метров ткани.

Определим сколько пищевого масла можно получить с 3,24 тонн хлопка-сырца. С одной тонны, как указано в задаче, получается 1,05 ц пищевого масла. А с 3,24 тонн будет получено в 3,24 раза больше масла

1,05 × 3,24 = 3,402 центнера пищевого масла

Определим сколько жмыха можно получить с 3,24 тонн хлопка-сырца. С одной тонны, как указано в задаче, получается 0,225 т жмыха. А с 3,24 тонн будет получено в 3,24 раза больше жмыха

0,225 × 3,24 = 0,729 тонн жмыха

Ответ: из 32,4 ц хлопка сырца можно получить 11016 метров ткани, 3,402 ц пищевого масла и 0,729 т жмыха.

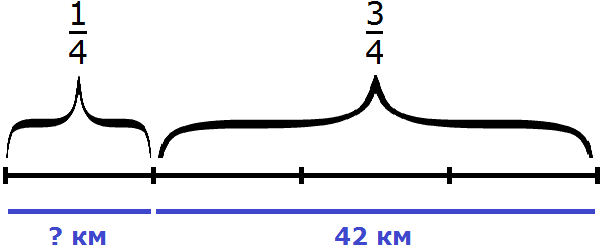
Решение

Зная, что 0,2 всего пути составляют 12 км, мы можем найти весь путь. Чтобы найти неизвестное число по десятичной дроби, нужно известное число разделить на десятичную дробь

Ответ: Туристы прошли 60 км.

Решение

Зная, что 0,7 книги составляют 56 страниц, мы можем узнать сколько всего страниц в книге. Чтобы найти неизвестное число по десятичной дроби, нужно известное число разделить на десятичную дробь

56 : 0,7 = 80 (страниц всего)

Узнаем сколько осталось прочитать

80 − 56 = 24 (страницы осталось прочитать)

Ответ: в книге 80 страниц. Прочитать осталось еще 24 страницы.

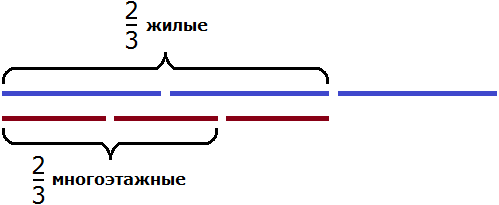
Решение

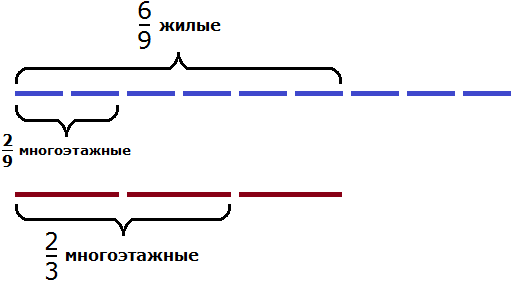
Разделим жилых домов на три части:

Чтобы узнать сколько многоэтажных домов приходится на две трети, умножим 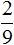на 2

Ответ: жилые многоэтажные дома составляют 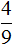всех зданий в городе.

Решение

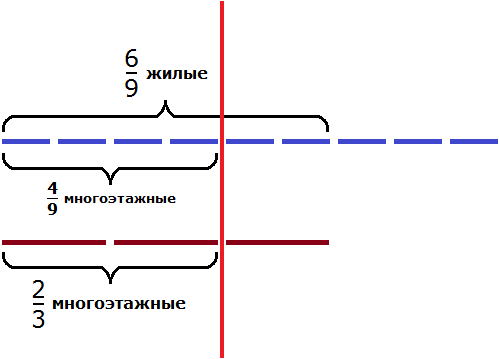
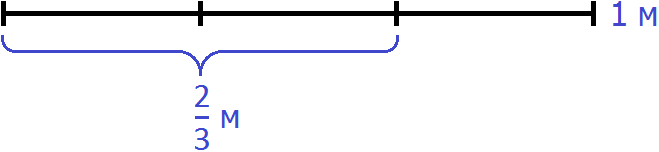
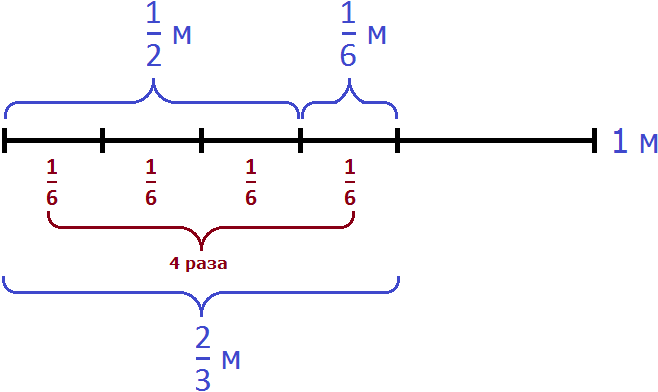
Изобразим схематически один метр веревки:

Выделим на этом рисунке метра:

Здесь же выделим метра

Не выделенным на м остался один кусочек. Узнаем, что это за кусочек. Для этого из вычтем

м это часть веревки, которую нужно отрезать. Тогда мы получим м веревки.

Теперь осталось узнать сколько раз м содержит м

Значит, чтобы не производя измерений от м веревки отрезать м, нужно эту веревку сложить вчетверо и отрезать одну часть. Оставшаяся часть и будет половиной от одного метра.

Ответ: чтобы от веревки, длина которой м отрезать м, нужно сложить эту веревку вчетверо и отрезать от неё одну часть. Оставшаяся часть станет м веревки.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

30 thoughts on “Задачи на дроби”

Здравствуйте! Очень благодарна вам за ваши труды. Очень все доступно объясняете.
В задаче №2 есть опечатка. В условии одна целая пять шестых часа, а в решении одна целая две трети.

Добавлю, что задача №2 в разделе самостоятельного решения.

Здравствуйте! Спасибо вам большое за задачи!
Но я никак не могу понять, почему в 16 задаче такое решение. Почему 3/7 оставшегося пути не вычисляются из 24км? Ведь второй день = 3/7 оставшегося пути, этот путь равен 24км. Он не может включать и второй день? Разве нет?

24 км это путь, пройденный в третий и четвертый дни. А во второй день было пройдено совсем другое расстояние.

Вообще, во второй, третий и четвертый дни всего было пройдено 42 км.

Найдите от 42 км сначала 3/7 пути, а потом 4/7 пути. Сразу станет всё понятно 😉

А откуда в 3-й задаче взялась дробь 15 на 15?

Источник