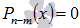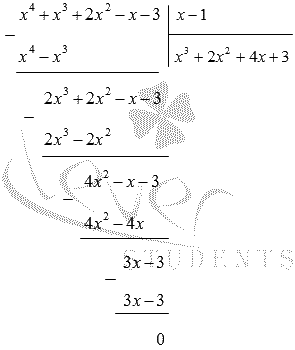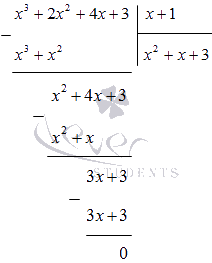Как решать уравнения высших степеней
Решение уравнений высших степеней
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
Уравнения высшей степени с целыми коэффициентами
Схема решения уравнения
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
Покажем на конкретном примере, как применяется такая схема решения.
Решение
Начнем с нахождений целых корней.
Перебираем возможные делители дальше, но подставляем их в равенство x 3 + 2 x 2 + 4 x + 3 = 0 :
Делим многочлен x 3 + 2 x 2 + 4 x + 3 на ( х + 1 ) в столбик:
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
| x i | коэффициенты многочлена | ||||
| 1 | 1 | 2 | — 1 | — 3 | |
| 1 | 1 | 1 + 1 · 1 = 2 | 2 + 2 · 1 = 4 | — 1 + 4 · 1 = 3 | — 3 + 3 · 1 = 0 |
Решение
Проверяем их по порядку:
| x i | коэффициенты многочлена | |||
| 1 | 1 | — 3 | — 6 | |
| 2 | 1 | 1 + 1 · 2 = 3 | — 3 + 3 · 2 = 3 | — 6 + 3 · 2 = 0 |
Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
Решение
Выполняем домножение 2 3 обеих частей уравнения:
Заменяем переменные y = 2 x :
Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.
«Решение уравнений высших степеней». 9-й класс
Разделы: Математика
Класс: 9
Оборудование: компьютер, проектор.
1 этап работы. Организационный момент.
2 этап работы. Мотивация и выход на постановку проблемы
Уравнение 
одно из важнейших понятий математики. Развитие методов решения уравнений, начиная с зарождения математики как науки, долгое время было основным предметом изучения алгебры.
В школьном курсе изучения математики очень много внимания уделяется решению различного вида уравнений. До девятого класса мы умели решать только линейные и квадратные уравнения. Уравнения третьей, четвёртой и т.д. степеней называются уравнениями высших степеней. В девятом классе мы познакомились с двумя основными приёмами решения некоторых уравнений третьей и четвёртой степеней: разложение многочлена на множители и использование замены переменной.
А можно ли решить уравнения более высоких степеней? На этот вопрос мы постараемся сегодня найти ответ.
3 этап работы. Повторить ранее изученный материал. Ввести понятие уравнения высших степеней.
1) Решение линейного уравнения.
Линейным называется уравнение вида 
, где 
по определению. Такое уравнение имеет единственный корень 
.
2) Решение квадратного уравнения.
Квадратным называется уравнение вида 
, где 
. Количество корней и сами корни определяются дискриминантом уравнения 
. Для 
уравнение корней не имеет, для 
имеет один корень (два одинаковых корня)
, для 
имеет два различных корня 
.
Из рассмотренных линейных и квадратных уравнений видим, что количество корней уравнения не более его степени. В курсе высшей алгебры доказывается, что уравнение 
-й степени 
имеет не более n корней. Что касается самих корней, то тут ситуация намного сложнее. Для уравнений третьей и четвёртой степеней известны формулы для нахождения корней. Однако эти формулы очень сложны и громоздки и практического применения не имеют. Для уравнений пятой и более высоких степеней общих формул не существует и существовать не может (как было доказано в XIX в. Н. Абелем и Э. Галуа).
Будем называть уравнения третьей, четвёртой и т.д. степеней уравнениями высших степеней. Некоторые уравнения высоких степеней удаётся решить с помощью двух основных приёмов: разложением многочлена 
на множители или с использованием замены переменной.
3) Решение кубического уравнения.
Решим кубическое уравнение 
Сгруппируем члены многочлена, стоящего в левой части уравнения, и разложим на множители. Получим:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три линейных уравнения:
Итак, данное кубическое уравнение имеет три корня: 
; 
;
.
4) Решение биквадратного уравнения.
Очень распространены биквадратные уравнения, которые имеют вид 
(т.е. уравнения, квадратные относительно 
). Для их решения вводят новую переменную 
.
Решим биквадратное уравнение 
.
Введём новую переменную и получим квадратное уравнение 
, корнями которого являются числа 
и 4.
Вернёмся к старой переменной 
и получим два простейших квадратных уравнения:
(корни и 
)
(корни 
и 
)
Итак, данное биквадратное уравнение имеет четыре корня:
; ;
.
Попробуем решить уравнение 
используя выше изложенные приёмы.
4 этап работы. Привести некоторые утверждения о корнях многочлена вида 
, где 
многочлен n-й степени
Приведём некоторые утверждения о корнях многочлена вида :
1) Многочлен -й степени имеет не более корней (с учётом их кратностей). Например, многочлен третьей степени не может иметь четыре корня.
2) Многочлен нечётной степени имеет хотя бы один корень. Например, многочлены первой, третьей, пятой и т.д. степени имеют хотя бы один корень. Многочлены чётной степени корней могут и не иметь.
4) Если число 
является корнем многочлена вида , то этот многочлен можно представить в виде произведения 
, где 
многочлен (
-й степени. Другими словами, многочлена вида можно разделить без остатка на двучлен 
. Это позволяет уравнение -й степени сводить к уравнению (-й степени (понижать степень уравнения).
5) Если уравнение 
со всеми целыми коэффициентами (причём свободный член 
) имеет целый корень , то этот корень является делителем свободного члена 
. Такое утверждение позволяет подобрать целый корень многочлена (если он есть).
Пример 1. Решим уравнение 
.
Таким образом, мы фактически разложили левую часть уравнения на множители:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем два уравнения:
Итак, данное уравнение имеет три корня:
Пример 2. Решим уравнение 
.
Если это уравнение имеет целый корень, то он является делителем свободного члена (9),т.е. равняется одному из чисел: 
;
. Проверим:
Значит, многочлен 
можно представить в виде произведения 
, т.е. многочлен 
можно без остатка разделить на двучлен 
. Выполним такое деление “уголком”:
Таким образом, мы разложили левую часть уравнения на множители:
Аналогичным образом поступим и с многочленом 
.
Если это уравнение 
имеет целый корень, то он является делителем свободного члена (9), т.е. равняется одному из чисел: ;. Проверим:
Значит, многочлен можно представить в виде
произведения 
, т.е. многочлен 
можно без остатка разделить на двучлен 
. Выполним такое деление “уголком”:
Таким образом, мы разложили левую часть исходного уравнения на множители:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три уравнения:
Итак, данное уравнение имеет четыре корня:
6 этап работы. Закрепление изученного материала.
Решите уравнения высших степеней, используя способ деления многочлена на многочлен “уголком”.
7 этап работы. Вывод урока.
8 этап работы. Домашнее задание.
Дома решить уравнения высших степеней, используя способ деления многочлена на многочлен “уголком” (раздать листы с заданиями).
Лекция по теме «Уравнения высших степеней. Методы их решения». 9-й класс
Разделы: Математика
Класс: 9
Формы, методы и педагогические приемы, которые используются учителем на уроке:
1. Организационный момент.
Формулировка темы урока: “Уравнения высших степеней. Методы их решения”.
2. Актуализация знаний учащихся.
Теоретический опрос – беседа. Повторение некоторых ранее изученных сведений из теории. Учащиеся формулируют основные определения и дают формулировки необходимых теорем. Приводят примеры, демонстрируя уровень полученных ранее знаний.
3. Изучение новой темы.
n = 1 – линейное уравнение.
n = 2 – квадратное уравнение. Формула дискриминанта. Формула для вычисления корней. Теорема Виета. Выделение полного квадрата.
n = 3 – кубическое уравнение.
Возвратное кубическое уравнение вида ax 3 + bx 2 + bx + a = 0. Решаем, объединяя члены с одинаковыми коэффициентами.
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. При применении этого метода необходимо сделать акцент на том, что перебор в данном случае конечный, и корни мы подбираем по определенному алгоритму в соответствии с теоремой о Z-корнях приведенного целого рационального уравнения с целыми коэффициентами.
Пример: x 3 – 9x 2 + 23x – 15 = 0. Уравнение приведенное. Выпишем делители свободного члена <+1; +3; +5; +15>. Применим схему Горнера:
Получаем 
(x – 1)(x 2 – 8x + 15) = 0 x1 = 1, x2 = 3, x3 = 5.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. При применении этого метода необходимо сделать акцент на том, что перебор в данном случае конечный и корни мы подбираем по определенному алгоритму в соответствии с теоремой о Q-корнях неприведенного целого рационального уравнения с целыми коэффициентами.
Пример: 9x 3 + 27x 2 – x – 3 = 0. Уравнение неприведенное. Выпишем делители свободного члена <+1; +3>. Выпишем делители коэффициента при старшей степени неизвестного. <+1; +3; +9> Следовательно, корни будем искать среди значений <+1; +
; +
; +3>. Применим схему Горнера:
Для удобства подсчета при подборе Q-корней бывает удобно сделать замену переменной, перейти к приведенному уравнению и подбирать Z-корни.
Формула Кардано. Существует универсальный метод решения кубических уравнений – это формула Кардано. Эту формулу связывают с именами итальянских математиков Джероламо Кардано (1501–1576), Николо Тарталья (1500–1557), Сципиона дель Ферро (1465–1526). Эта формула лежит за рамками нашего курса.
n = 4 – уравнение четвертой степени.
Метод замены переменной.
Решаем, объединяя члены с одинаковыми коэффициентами, путем замены вида
Пример 3. Замена общего вида (вытекает из вида конкретного уравнения).
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Формула общего вида. Существует универсальный метод решения уравнений четвертой степени. Эту формулу связывают с именем Людовико Феррари (1522–1565). Эта формула лежит за рамками нашего курса.
n > 5 – уравнения пятой и более высоких степеней.
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Метод замены переменной. Использование однородности.
Не существует формулы общего вида для решения целых уравнений пятой степени (это показали итальянский математик Паоло Руффини (1765–1822) и норвежский математик Нильс Хенрик Абель (1802–1829)) и более высоких степеней (это показал французский математик Эварист Галуа (1811–1832)).
4. Подведение итогов.
Резюме: Теперь мы овладели основными методами решения различных уравнений высших степеней (для n > 3). Наша задача научиться эффективно использовать перечисленные выше алгоритмы. В зависимости от вида уравнения мы должны будем научиться определять, какой способ решения в данном случае является наиболее эффективным, а также правильно применять выбранный метод.
5. Домашнее задание.
[1]: п.7, стр. 164–174, №№ 33–36, 39–44, 46,47.
[4]: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.
Возможные темы докладов или рефератов по данной тематике:
Анализ усвоения материала и интереса учащихся к теме:
Опыт показывает, что интерес учащихся в первую очередь вызывает возможность подбора Z-корней и Q-корней уравнений при помощи достаточно простого алгоритма с использованием схемы Горнера. Также учащиеся интересуются различными стандартными типами замены переменных, которые позволяют существенно упрощать вид задачи. Особый интерес обычно вызывают графические методы решения. В этом случае дополнительно можно разобрать задачи на графический метод решения уравнений; обсудить общий вид графика для многочлена 3, 4, 5 степени; проанализировать, как связано число корней уравнений 3, 4, 5 степени с видом соответствующего графика. Ниже приведен список книг, в которых можно найти дополнительную информацию по данной тематике.
Решение уравнений высших степеней.
В общем случае уравнение степени выше четвертой не разрешимо в радикалах. Однако, иногда можно отыскать корни многочлена, который находится в левой части уравнения высшей степени, представив его в виде призведения многочленов степени не выше четвертой. Таким образом, разложение многочлена на множители лежит в основе решения таких уравнений, поэтому, рекомендуем подробно изучить этот раздел, прежде чем двигаться дальше.
Достаточно часто рассматриваются уравнения высших степеней с целыми коэффициентами. В этом случае можно попытаться найти рациональные корни уравнения, после чего можно разложить на множители многочлен, находящийся в левой части исходного уравнения, тем самым перейти к нахождению корней уравнения, степень которого будет ниже.
В этой статье как раз разберемся с решением уравнений высших степеней с целыми коэффициентами.
Уравнения высших степеней с целыми коэффициентами.
Любое уравнение вида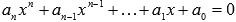 
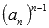
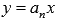
можно свести к приведенному уравнению той же степени домножив обе его части на 
и выполнив замену переменной вида 
:
Полученные коэффициенты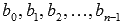 
тоже будут целыми.
Таким образом, будем решать приведенное уравнение степени n с целыми коэффициентами вида 
.
Находим целые корни уравнения.
Целые корни уравнения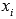 
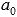
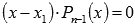
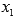
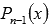
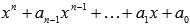
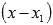
, i=1, 2, …, m ( m – количество целых корней уравнения) находятся среди делителей свободного члена 
. То есть, первым делом выписываем делители свободного члена и подставляем их по очереди в исходное равенство для проверки. Перебираем их по очереди, пока не получим тождество. Как только тождество получено, то первый целый корень уравнения найден и уравнение предстает в виде 
, где 
— корень уравнения, а 
— частное от деления 
на 
.
Продолжаем подставлять выписанные ранее делители в уравнение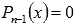 
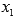
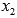
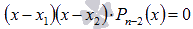
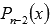
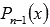
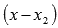
, начиная с (так как корни могут повторяться). Как только получаем тождество, то корень 
найден и уравнение предстает в виде 
, где 
— частное от деления 
на 
.
Дробных корней приведенное уравнение с целыми коэффициентами иметь не может.
Находим оставшиеся корни (иррациональные и/или комплексные) из уравнения 
любым способом.