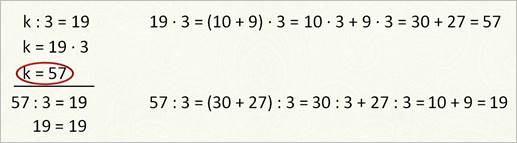Как решать уравнения умножение

Уравнения на умножение

1) Формировать умение строить алгоритм на примере построения алгоритма решения простых уравнений на умножение, формировать умение использовать построенный алгоритм при решении уравнения.

2) Тренировать вычислительный навык, решать текстовые задачи.

Мыслительные операции, необходимые на этапе проектирования: анализ, синтез, сравнение, аналогия.

1 этап. Мотивация к учебной деятельности

1) мотивировать учащихся к учебной деятельности,

Организация учебного процесса на этапе 1:

— Какую тему мы сейчас изучаем на уроках математики? (Умножение и деление)

— В каких заданиях применяем эти действия? (В решении примеров, задач)

— Хотите узнать, какие еще есть задания, в которых мы можем использовать эти действия? (Да)

Ребята, посмотрите, кто сегодня пришел к нам на урок? Вы их узнали? Что вы знаете об этих героях? (…)

(Появляются знаки вопроса). Что происходит? Колобки озадачены и расстроены. Они хотели выполнить задание, а у них впервые не получилось. Они не знают, как открывать новые знания. Поможем? (…)

А можно ли приниматься за работу с таким настроением, как у колобков? (Нельзя, не будет результата)

Давайте улыбнемся друг другу и пожелаем удачи! Ну что же, будем действовать по плану открытия нового знания. Вам он хорошо знаком.

2 этап. Актуализация знаний и фиксация затруднения в пробном действии

1) актуализация изученных способов действий, достаточных для построения, их вербальная и знаковая фиксация и обобщение;

2) актуализация мыслительных и познавательных процессов, достаточных для построения нового знания;

3) мотивация к пробному учебному действию и его самостоятельному осуществлению;

4) фиксация учащимися индивидуальных затруднений в выполнении пробного учебного действия или его обосновании.

Организация учебного процесса на этапе 2:

1) Актуализация формул нахождения площади и неизвестной стороны прямоугольника.

С чего начнем? (С повторения). Мы должны повторить все, что знаем? (Нет, только то, что нам пригодится для открытия нового знания)

— Что нужно найти в этом задании? (Площадь прямоугольника)

— Как найти площадь прямоугольника? (Чтобы найти площадь прямоугольника, надо длину умножить на ширину)

Появляется формула площади.

Учащиеся выполняют задание.

— Чему равна площадь? (18 кв. м)

— Кто получил другой ответ?

— Как найти неизвестную сторону прямоугольника? (Чтобы найти неизвестную сторону прямоугольника надо площадь разделить на известную сторону)

— Появляется формула нахождения неизвестной стороны прямоугольника.

— Составьте обратную задачу, в которой нужно найти длину прямоугольника (…)

— Запишем решение обратной задачи.

Ученик, составивший обратную задачу, решает ее на доске: 18 :3=6(м) – длина

— Теперь составьте другую обратную задачу.

Ученик, составивший обратную задачу, решает ее на доске: 18:6=3 (м) – ширина

У кого в этом задании не было ошибок? Поставьте себе знак + на маршрутном листе рядом с повторением. Кто допустил ошибку? Почему возникла ошибка? Вы поняли ее причину? Исправьте ошибку. Что вы себе поставите? (? и +).

2) Актуализация алгоритма решения уравнений на сложение и вычитание.

— Запишите: сумма Х + 5 равна 7. Как можно назвать эту запись? (Уравнение)

— Что такое уравнение? (Равенство, в котором есть неизвестное число, называют уравнением)

— Что поможет нам решить это уравнение? (Эталон решения уравнений на сложение)

Один ученик у доски с комментированием. (Обозначу компоненты уравнения, подчеркну части, целое (сумму) обведу. Вижу, что неизвестна часть. Чтобы найти неизвестную часть, надо из суммы вычесть известную часть.

У кого в этом задании не было ошибок? Поставьте себе знак + на маршрутном листе рядом с повторением. Кто допустил ошибку? Почему возникла ошибка? Вы поняли ее причину? Исправьте ошибку. Что вы себе поставите? (- и +).

— Почему мы повторили именно это? (Это пригодится нам для открытия нового знания)

— Какой следующий шаг? (Пробное действие) Для чего оно нужно? (Чтобы понять, чего мы не знаем)

Учитель раздает учащимся карточки с заданием для пробного действия:

— Какое задание нужно выполнить? (Решить уравнение)

— С каким действием? (С умножением)

— А что нового в этом задании? (Мы не решали уравнения на умножение)

Попробуйте выполнить это задание. (30 сек.)

— Кто не выполнил задание?

Что вы не смогли сделать? (Мы не смогли решить уравнение)

— Кто нашел корень уравнения? Какие результаты у вас получились?

Учитель фиксирует результаты на доске рядом с пробным действием

— Обоснуйте свое мнение.

Что вы не можете сделать? (Мы не можем обосновать свой ответ.)

У вас возникло. (затруднение). Поставим… (знак вопроса) рядом с пробным действием на маршрутном листе.

— Какой следующий шаг на уроке? (Разобраться, в чем у нас затруднение)

— А раз возникло затруднение, надо…(Остановиться и подумать)

3 этап. Выявление места и причины затруднения

1) восстановить выполненные операции и зафиксировать место затруднения;

2) соотнести свои действия с используемым способом действий и на этой основе выявить и зафиксировать во внешней речи причину затруднения.

Организация учебного процесса на этапе 3:

— Какое задание вы должны были выполнить? (Мы должны были решить уравнение на умножение)

— Как рассуждали, выполняя пробное действие? (Пытались воспользоваться известным алгоритмом решения уравнений …)

— В чем затруднение? (Алгоритм не подходит)

Почему же возникло затруднение? (У нас нет способа для решения уравнений на умножение)

Вы поняли, чего вы не знаете? (Да). Поставьте себе знак + на маршрутном листе рядом с третьим шагом.

4 этап. Построение проекта выхода из затруднения

1) согласовать и зафиксировать цель и тему урока;

2) построить план и определить средства достижения цели.

Организация учебного процесса на этапе 4:

— Мы поняли, чего мы не знаем, теперь можем… (Сами открывать способ)

Сначала нужно поставить цель. Если вы не знаете способа решения уравнений на умножение, значит, ваша цель… (Открыть способ решения таких уравнений)

— Сформулируйте тему нашего урока (…)

Написать тему на доске:

— Будем действовать, как настоящие сыщики. Составим план действий. Слайд

— Давайте подумаем, что нам может помочь. Вспомните, вы повторили в самом начале урока. (Алгоритм решения уравнений на сложение, формулу нахождения площади)

— Какая формула может нам помочь? (Формула нахождения площади и неизвестной стороны прямоугольника)

— Пробуем применить формулу площади прямоугольника.

— Предлагаю воспользоваться известным вам алгоритмом решения уравнений на сложение.

Заменим п.1 на Обозначим компоненты уравнения на модели прямоугольника.

— Остальные пункты алгоритма вам подходят?

— Используя этот алгоритм, можно попробовать решить уравнение?

— Что сделаем, чтобы было удобно пользоваться этим правилом всегда? (Запишем правило в общем виде)

Запишем правило в общем виде.

— Какими средствами будем пользоваться?

Пробуем применить формулу площади прямоугольника…

Запишем правило в общем виде.

Средства: модель прямоугольника, алгоритм.

5 этап. Реализация построенного проекта

1) реализовать построенный проект в соответствии с планом;

2) зафиксировать способы записи выражений на эталоне;

3) организовать фиксацию преодоления затруднения;

4) организовать уточнение общего характера нового знания.

Организация учебного процесса на этапе 5:

Я предлагаю поработать вам в группах. Назовите правила работы в группах.

Правила работы в группах

1. В группе должен быть ответственный.

2. Один говорит, другие слушают.

3. Свое несогласие высказывать вежливо..

4. Работать должны все.

Учащиеся объединяются в группы.

— Выполните план в группах.

Ответственный от каждой группы получает задание.

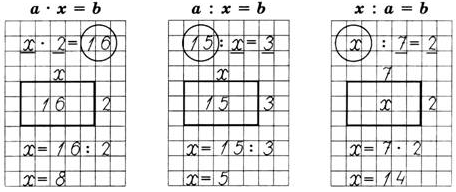
1. Воспользуюсь моделью прямоугольника, нанесу компоненты уравнения на модель.

2. Применю правило площади прямоугольника. (Чтобы найти неизвестную сторону прямоугольника надо площадь разделить на известную сторону)

3. Найду корень уравнения

Х = ___________________

Мы обозначили на модели прямоугольника числа. Видно, что неизвестна сторона прямоугольника. Чтобы найти неизвестную сторону прямоугольника, надо площадь разделить на известную сторону. Выполнили вычисления и нашли корень уравнения, х=5.

— Что осталось сделать по плану? (Записать уравнение в общем виде)

— Как записать уравнение в общем виде? (С помощью букв латинского алфавита)

— Как обозначите в уравнении числа, которые являются сторонами прямоугольника? (Подчеркнем)

— Число, которое является площадью, предлагаю взять в прямоугольник, почему это удобно? (Напоминает о формуле, которой мы пользуемся)

— Нужно ли будет составлять другой эталон для случая, где х стоит на месте другого множителя? (Нет)

— Почему? (Можно воспользоваться переместительным свойством умножения)

— Как проверить свое открытие? Какие ключи к знаниям у нас есть? (Посмотреть в учебнике)

Откройте учебники на стр.1. Прочитайте правило.

Молодцы! Вы помогли колобкам. Слайд (аплодисменты).

Давайте теперь вернемся к пробному действию.

Дописать необходимое на доске.

Смогли вы преодолеть затруднение? (Да). Поставим себе знак + на маршрутном листе.

На обычной доске под шагом “Сам найду способ” прикрепить новые эталоны.

Что вы теперь сможете делать с помощью новых знаний? (Решать уравнения)

6 этап. Первичное закрепление

1) организовать усвоение детьми нового способа действий при решении уравнений на умножение с их проговариванием во внешней речи.

Организация учебного процесса на этапе 6:

1) Фронтальная работа. На доске левая часть-алгоритм, правая – уравнение+модель.

2) 4 · х=8; 3 · х=9; х · 4=12.

3) Учитель открывает на доске задание на закрепление. Учащиеся по цепочке выходят к доске и выполняют задание с комментированием. Вариант комментирования:

— Сначала обозначу площадь прямоугольника квадратом, а стороны подчеркну. В данном уравнении неизвестна сторона прямоугольника. Значит, надо площадь прямоугольника разделить на известную сторону. Восемь разделить на 4 будет 2, х равен 2.

Дальнейшее выполнение задания комментируется аналогично.

Физминутка гимнастика для глаз.

Мы немного отдохнём. и на всё ответ найдём.
На носочки встанем, руки вверх потянем.
Руки на пояс, наклоны вперёд.
Теперь попрыгаем, и сядем на места!

Сейчас все отдохнули, и новая забота:

Нужно сделать на “отлично” парную работу.

Учитель раздает карточки с заданием для работы в парах.

Учащиеся выполняют задания в парах с комментированием. Проверка организуется по образцу Д-7.

— Проверьте свои результаты.

Исправьте ошибки. У кого в этом задании не было ошибок? Поставьте себе знак + на маршрутном листе рядом с 5-м шагом. Кто допустил ошибку? Почему возникла ошибка? Вы поняли ее причину? Исправьте ошибку. Что вы себе поставите? (? и +)

— Какой следующий шаг на уроке? (Проверить себя, справимся ли мы самостоятельно)

7 этап. Самоконтроль с самопроверкой по эталону

1) тренировать способность к самоконтролю и самооценке;

2) проверить умение решать уравнения на умножение.

Организация учебного процесса на этапе 7:

— Выполните данные уравнения самостоятельно. Учащиеся выполняют самостоятельную работу на карточках

— Проверка организуется по эталону Д-8.

— Сделайте вывод. (Нужно еще потренироваться.)

— Сделайте вывод. (Мы все хорошо усвоили.)

— У кого в этом задании не было ошибок? Поставьте себе знак + на маршрутном листе рядом с 5-м шагом. Кто допустил ошибку? Почему возникла ошибка? Вы поняли ее причину? Исправьте ошибку. Что вы себе поставите? (? и +).

8 этап. Включение в систему знаний и повторение

1) включить новое знание в систему знаний;

2) тренировать умение решать задачи.

Организация учебного процесса на этапе 8:

— Что нужно знать, чтобы правильно решать уравнения на умножение? (Таблицу умножения и деления, формулу площади). Предлагаю вам решить задачу №4 стр.2.

Учащиеся выполняют задание. Проверка организуется по образцу Д-9.

— В чем ошибка? (В выборе правила, в вычислениях, …)

9 этап. Рефлексия учебной деятельности на уроке

Цели:

1) зафиксировать новое содержание, изученное на уроке;

2) оценить свою работу и работу класса на уроке;

4) наметить направления будущей учебной деятельности;

3) обсудить домашнее задание.

Организация учебного процесса на этапе 9:

— Какую цель вы перед собой ставили? (…)

— Достигли ли вы цели? (Докажите)

— Я предлагаю вам оценить свою работу на уроке. Посмотрите еще раз на свои планы урока, посмотрите, сколько у вас плюсов.

— На обычной доске изображение колобков по отдельности. Один улыбается. Те из вас, кто считает, что понял и запомнил новую тему, возьмите восклицательные знаки и прикрепите их рядом с улыбающимся Колобком. Те, кто в чем-то еще не уверен, у кого остались вопросы, кто допустил ошибки в самостоятельной работе – прикрепите вопросительный знак рядом с серьезным Колобком. Вы потренируетесь и обязательно преодолеете свое затруднение.

— Вы сегодня очень хорошо поработали, но значит ли это, что больше не надо тренироваться? (Надо выполнить домашнюю работу)

Источник

Простые уравнения на умножение и деление. 2 класс.

Большие затруднения для младшего школьника вызывает умение решать данный вид уравнений.

Мы уже знаем, что простые уравнения – это равенства, где есть одна переменная (неизвестное число).

Во 2 классе дети учатся решать простые уравнения на умножение и деление (5 • х = 10, х: 3 = 12, 12 : х = 4)
Для решения этих уравнений правила о части и целом использовать нельзя, потому что второй множитель (х • 3 = 12) — это не часть, а число равных частей, на которое разбили целое.

Сегодня мы рассмотрим несколько вариантов решения:

Если вы видите уравнение х: 4 = 8 и сомневаетесь, нужно х = 8 • 4 или х = 8 : 4, поступайте так: пишите на черновике простой пример на то действие, которое хочет вас запутать. Действие у нас – деление. Давайте напишем 6 : 2 = 3 и закроем число, которое в нашем уравнении неизвестно — это первое число, значит, закрываем число 6. И как шестерку найти, имея 2 и 3? Надо – перемножить тройку с двойкой. Значит, и в нашем уравнении нужно перемножать числа, но никак не делить:

Этот способ выручает, когда мы решаем вот такие уравнения: 4857 + у = 10208.
Большие числа часто пугают, а они живут по тем же законам, что и маленькие числа. Поэтому пишем, например 4 + 1 = 5. И закрываем число 1. Чтобы его найти, нужно из 5-и вычесть 1. Значит, 10208 – 4857:
у = 10208 — 4857
у = 5351

2. Зная правила нахождения стороны и площади прямоугольника.

3. Используя взаимосвязи между компонентами действий.

Этот способ необходим при ответе у доски.
Ученики младших классов обязаны овладеть математической речью, а для этого нужно знать, как называются компоненты при различных действиях:
Слагаемое, слагаемое, сумма.

Уменьшаемое, вычитаемое, разность.

Множитель, множитель, произведение.

Делимое, делитель, частное.

Например, в решении уравнения x • 3 = 6 объясняем так: чтобы найти первый множитель, надо значение произведения разделить на второй множитель.

В уравнении неизвестно слагаемое:

чтобы найти второе слагаемое, надо из суммы вычесть первое слагаемое:

4. Использование памятки:

х + 6 = 124 х – 3 = 71 х × 3 = 183 х : 2 = 15	Если переменная х находится вначале уравнения, то находи ее действием, противоположным тому, что в уравнении. То есть для сложения – вычитанием и наоборот. Для умножения – делением и наоборот.
12 + х = 138 146 – х = 59 30 × х = 3000 500 : х = 4	Если х находится посередине уравнения, то или вычитай, или дели.

Использовать памятку – самый простой и легкий способ решать простые уравнения правильно.

Данная памятка – результат многолетней работы в школе.

Поэтому вы можете ее скачать, распечатать и постоянно ей пользоваться.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.9 / 5. Количество оценок: 74

Источник

Решение простых уравнений. 5 класс

Уравнение — это равенство, содержащее букву, значение которой надо найти.

В уравнениях неизвестное обычно обозначается строчной латинской буквой. Чаще всего используют буквы « x » [икс] и « y » [игрек].

Решив уравнение, всегда после ответа записываем проверку.

Информация для родителей

Уважаемые родители, обращаем ваше внимание на то, что в начальной школе и в 5 классе дети НЕ знают тему «Отрицательные числа».

Поэтому они должны решать уравнения, используя только свойства сложения, вычитания, умножения и деления. Методы решения уравнений для 5 класса приведены ниже.

Не пытайтесь объяснить решение уравнений через перенос чисел и букв из одной части уравнения в другую с изменением знака.

Освежить знания по понятиям, связанным со сложением, вычитанием, умножением и делением вы можете в уроке «Законы арифметики».

Решение уравнений на сложение и вычитание

Как найти неизвестное слагаемое

x + 9 = 15Как найти неизвестное
уменьшаемое

x − 14 = 2Как найти неизвестное
вычитаемое

Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое.

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность.

x + 9 = 15
x = 15 − 9
x = 6
Проверка

6 + 9 = 15
15 = 15x − 14 = 2
x = 14 + 2
x = 16
Проверка

16 − 2 = 14
14 = 145 − x = 3
x = 5 − 3
x = 2
Проверка

Решение уравнений на умножение и деление

Как найти неизвестный множитель

y · 4 = 12Как найти неизвестное
делимое

y : 7 = 2Как найти неизвестный
делитель

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

Чтобы найти неизвестное делимое, надо частное умножить на делитель.

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Источник

Решение уравнений

Урок 34. Математика 3 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение уравнений»

Сегодня я хочу вам напомнить о том, что такое уравнения, и как решать уравнения, в которых стоят знаки умножения и деления. А начну я с того, почему уравнение так называется.

Уравнение – это математическое равенство, в котором есть одно или даже несколько неизвестных. Эти неизвестные обычно обозначаются буквами латинского алфавита (а + 12 = 17, 78 – в = 24, с – 32 = 19, х × 4 = 56, 98 : у = 7, k : 3 = 19, 3z – 2r = 2).

Видите, во всех этих записях стоит знак равно.

Это значит, что при решении уравнений надо найти такое значение неизвестного, при котором левая часть уравнения будет равна правой.

Вы уже умеете решать уравнения, в которых стоят знаки плюс или минус. Помните, для решения таких уравнений мы пользуемся правилами:

* Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

* Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность.

* Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

А ещё решать уравнения нам помогали схемы.

На первой из них видно, что слагаемые являются частями. Поэтому их мы находим вычитанием. Ведь если нам, например, надо взять часть яблока или груши, мы её отрежем, то есть вычтем.

А вот сумма – это целое, получить которое можно сложением частей.

Вторая схема нам подсказывает, что целым является уменьшаемое. А так как это целое, то его мы будем находить действием сложения. А вот вычитаемое – часть, поэтому его мы найдём вычитанием.

А как же решать уравнения, если в них не действия сложения или вычитания, а умножение и деление? Вот, например, такое уравнение.

В нём надо найти такое значение икс, при умножении которого на четыре получится пятьдесят шесть. Ещё во втором классе мы с вами говорили о связи между компонентами и результатом действия умножения:

Если произведение двух множителей разделить на один из них, то получится другой множитель.

Значит, неизвестный множитель надо находить действием деления. Найдём его. Решение будем записывать под уравнением.

Пишем: икс равен частному чисел пятьдесят шесть и четыре. Так-так, надо посчитать. Все расчёты можно записывать справа от уравнения.

Пятьдесят шесть это сорок и шестнадцать. Делим каждое на четыре. Десять и четыре. Четырнадцать. Отступаю клеточку вниз и пишу: икс равен четырнадцати. Но, конечно, не забываю и про проверку. Черта, под которой пишу наше уравнение точно такое же, как оно было записано в верхней строчке, только вместо буквы подставляю её значение. Получился решённый пример. Но мы обязательно должны проверить, правильно ли он решён. Для этого выполним действие, которое находится слева от знака равно. Умножим четырнадцать на шесть.

Полученное число пишем внизу под левой частью уравнения. А число из правой части уравнения просто переносим. Видите, результат действия в левой части и правая часть между собой равны. Значит, уравнение решено верно. Корень уравнения равен четырнадцати.

А как же решать уравнения, в которых стоит знак деления?

И тут нам на помощь придут правила связи между компонентами и результатом действия деления.

Вот посмотрите на это уравнение.

В нём неизвестно делимое. Вспоминаем правило: Чтобы найти неизвестное делимое, надо частное умножить на делитель.

Принимаемся за работу. К равно девятнадцать умножить на три. Получилось пятьдесят семь. Значит, k равно пятидесяти семи.

Подчёркиваю, и списываю наше уравнение, заменив букву k полученным значением. А теперь обязательно выполняю действие из левой части нашего уравнения. Пятьдесят семь разделить на три. Получилось девятнадцать. И справа тоже число девятнадцать. Есть равенство. Значит, уравнение решено верно и корень его равен пятидесяти семи.

А если в уравнении на деление надо найти неизвестный делитель, как вот в этом уравнении?

И вновь на помощь приходит правило: Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Решаем уравнение: 98 : у = 7.

Игрек равен частному чисел девяносто восемь и семь. Игрек равен четырнадцати. Проверяем. Записываем уравнение, заменив букву на число четырнадцать. Здесь придётся воспользоваться методом подбора, то есть умножить четырнадцать на такое однозначное число, чтобы в ответе получилось девяносто восемь. Но, так как справа записано число семь, попробую-ка я сразу умножить четырнадцать на семь. Отлично, произведение чисел четырнадцать и семь равно девяносто восьми. Все получилось. Корень уравнения равен четырнадцати.

Для решения этих уравнений мы воспользовались правилами связи между компонентами и результатом действий умножения и деления.

* Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

* Чтобы найти неизвестный делитель, надо делимое разделить на частное.

* Чтобы найти неизвестное делимое, надо частное умножить на делитель.

Но вот некоторым ребятам бывает трудно запоминать все правила. А нельзя ли воспользоваться какой-нибудь короткой схемой, как мы это сделали при решении уравнений на сложение и вычитание? А почему бы и нет.

Для решения уравнений с действием умножения воспользуемся схемой, которой пользовались при решении уравнений, в которых стоит знак плюс. А для решения уравнений с действием деления воспользуемся схемой, которой пользовались при решении уравнений, в которых стоит знак минус. Просто заменим в схемах знаки.

Посмотрите, в первой схеме множители – это части, а произведение – целое. Части мы будем находить действием, обратным умножению – делением. А ведь наше правило об этом и говорит.

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

Вот, допустим, надо решить такое уравнение: три умножить на икс равно тридцать шесть.

Подставляем его в нашу схему.

Икс – это часть. Находим делением. Икс равен двенадцати. Проверяем. Умножаем три на двенадцать. Тридцать шесть. И справа тридцать шесть. Уравнение решено верно. Схема работает!

А теперь проверим вторую схему. Игрек разделить на семь равно одиннадцать

Подставили его в схему.

Найти надо делимое. Это целое. Находим умножением. И правило об этом говорит.

Чтобы найти неизвестное делимое, надо частное умножить на делитель.

И здесь схема сработала. А справится ли наша схема с неизвестным делителем, попробуйте проверить сами. Решите вот это уравнение.

Ну вот и всё. Пришла пора нам с вами прощаться. Но я думаю, вы запомните правила, которые помогут вам решить любое уравнение.

* Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

* Чтобы найти неизвестное делимое, надо частное умножить на делитель.

* Чтобы найти неизвестный делитель, надо делимое разделить на частное.

А если вдруг забудете его, вы всегда сможете воспользоваться схемами.

А я сегодня прощаюсь с вами. До встречи, ребята!

Источник