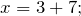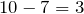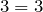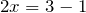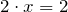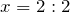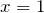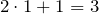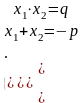Как решать уравнения алгоритм

Алгоритм решения уравнений

Решить уравнение — это значит найти неизвестную величину, после подстановки которой в уравнение получаем верное равенство.

Алгоритм решения уравнения

Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое

Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность

Чтобы найти неизвестный множитель, надо произведение поделить на известный множитель

Чтобы найти неизвестное делимое, необходимо частное умножить на делитель

Чтобы найти неизвестный делитель, надо делимое поделить на частное

Примеры решения задач

Задание	Решить уравнение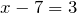
Решение	1) Записываем уравнение: ;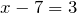

2) данное уравнение на нахождение разности;

3) неизвестным является уменьшаемое. Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое:

4) ;

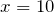
5) сделаем проверку, для этого подставим полученное значение 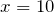в исходное уравнение:

Получили верное равенство, корень найден верно.

Ответ

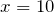
Задание	Решить уравнение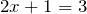
Решение	Заданное уравнение содержит неизве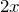стное слагаемое , чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое:

Получили простейшее уравнение на нахождение произведения. Чтобы найти неизвестный множитель, надо произведение поделить на известный множитель:

— верное равенство.

Ответ

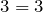
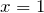
Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Источник

Алгоритм решения уравнений.

Алгоритм решения уравнений 7 класс.Решение линейных уравнений по алгоритму.

Просмотр содержимого документа
«Алгоритм решения уравнений.»

2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный)

3. Привести подобные слагаемые в каждой части уравнения.

4. Разделить обе части уравнения на коэффициент при неизвестном.

(Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. )

2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный)

3. Привести подобные слагаемые в каждой части уравнения.

4. Разделить обе части уравнения на коэффициент при неизвестном.

(Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. )

2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный)

3. Привести подобные слагаемые в каждой части уравнения.

4. Разделить обе части уравнения на коэффициент при неизвестном.

(Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. )

2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный)

3. Привести подобные слагаемые в каждой части уравнения.

4. Разделить обе части уравнения на коэффициент при неизвестном.

(Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. )

2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный)

3. Привести подобные слагаемые в каждой части уравнения.

4. Разделить обе части уравнения на коэффициент при неизвестном.

(Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. )

2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный)

3. Привести подобные слагаемые в каждой части уравнения.

4. Разделить обе части уравнения на коэффициент при неизвестном.

(Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. )

2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный)

3. Привести подобные слагаемые в каждой части уравнения.

4. Разделить обе части уравнения на коэффициент при неизвестном.

(Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. )

2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный)

3. Привести подобные слагаемые в каждой части уравнения.

4. Разделить обе части уравнения на коэффициент при неизвестном.

(Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. )

Источник

Виды и алгоритмы решения уравнений

Содержимое разработки

Уравнением называется равенство, содержащее неизвестные переменные.

Уравнение с одним неизвестным x записывается в виде f(x)=g(x).

Корнем уравнения называется всякое число, при подстановке которого вместо неизвестной в обе части уравнения получается верное числовое равенство.

Решить уравнение – значит найти все его корни, или доказать, что их нет.

Областью определения уравнения или областью допустимых значений уравнения (ОДЗ) называется множество всех тех значений переменных x, при которых оба выражения f(x) и g(x) имеют смысл.

Два уравнения называются равносильными на данном числовом множестве, если они имеют одни и те же корни или оба не имеют корней.

Линейным уравнением с одним неизвестным называется уравнение вида ax + b = 0, где а и b – действительные числа, x – неизвестная величина.

Любой член уравнения можно перенести из одно части в другую, изменив его знак на противоположный.

Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.

При решении линейного уравнения возможны случаи:

• если a = 0, b ≠ 0, то 0 ⋅ x + b = 0, 0 ⋅ x = −b ⇒ корней нет.

Алгоритм решения уравнения:

Переносят члены, содержащие неизвестное, в левую часть, а члены, не содержащие неизвестного, в правую часть.

Приводят подобные слагаемые.

Делят обе части уравнения на коэффициент при неизвестном, если он не равен нулю.

Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0, где x – переменная, a, b, c – некоторые числа, причем, а ≠ 0.

а – первый коэффициент; b – второй коэффициент; с – свободный член.

Квадратные уравнения, в которых хотя бы один из коэффициентов b или с равен нулю, называются неполными.

1) Если ac 0 – корней нет

х₁ = — c : a

Алгоритм решения квадратного уравнения

Сравнить дискриминант с 0.

D = 0 ⇒ два равных корня x_1,2 = _,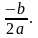

D 0 ⇒ два корня x₁ = 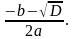x₂ =

Квадратное уравнение, первый коэффициент которого равен 1, называется приведенным:

Корни приведенного квадратного уравнения можно найти по формулам:

если D = 0, то x_1,2 =

Сумма корней квадратного уравнения ax 2 + bx + c = 0 равна ,

произведение корней равно

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

х 2 + pх + q = 0,

где х₁ и х₂ – корни приведенного квадр. уравнения.

Другие способы решения уравнений.

Уравнения третьей, четвертой и т.д. степени могут решаться разными способами.

Разложение на множители.

Записать уравнение в виде многочлена стандартного вида приравненного к 0.

Разложить многочлен на множители любым способом.

Использовать свойство: произведение равно 0, если хотя бы один из множителей равен 0. Для этого каждый множитель приравниваем к 0.

Решить получившиеся уравнения.

Введение новой переменной

Обозначить повторяющееся выражение, содержащее переменную другой буквой.

Записать уравнение, заменив сложные выражения новой переменной.

Решить получившееся уравнение.

Подставить найденные значения переменной в выражение для замены исходной переменной.

Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.

Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.

Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное числовое равенство.

Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.

Системы двух уравнений с двумя неизвестными

Способы решения систем двух уравнений с двумя неизвестными

из одного уравнения системы ( всё равно из какого) выразить одно неизвестное через другое, например у через х.

полученное выражение подставить в другое уравнение системы, получится одно уравнение с одним неизвестным х.

решить это уравнение, найти значение х.

подставив найденное значение х в выражение для у, найти значение у.

способ алгебраического сложения, нужно

уравнять модули коэффициентов при одном из неизвестных.

складывая и вычитая полученные уравнения, найти одно неизвестное.

подставляя найденное значение в одно из уравнений исходной системы, найти второе неизвестное.

Построить графики каждого из уравнений системы в одной системе координат

Найти координаты точки пересечения построенных прямых (если они пересекаются)

Возможны три случая взаимного расположения двух прямых- графиков линейных уравнений системы.

Прямые пересекаются, т.е. имеют одну общую точку. Система уравнений имеет единственное решение.

Прямые параллельны, т.е. не имеют общих точек. Система уравнений не имеет решений.

Прямые совпадают. Система уравнений имеет бесконечно много решений.

Способ введения новых переменных –применяется в том случае, если выражения с переменными имеют сложный вид.

Обозначить выражения, содержащие переменные другими буквами.

Записать уравнения системы, заменив сложные выражения новыми буквами.

Решить получившиеся уравнения.

Подставить найденные значения букв в выражения для замены переменных.

Другие способы решения уравнений.

Уравнения третьей, четвертой и т.д. степени могут решаться разными способами.

Разложение на множители.

Записать уравнение в виде многочлена стандартного вида приравненного к 0.

Разложить многочлен на множители любым способом.

Использовать свойство: произведение равно 0, если хотя бы один из множителей равен 0. Для этого каждый множитель приравниваем к 0.

Решить получившиеся уравнения.

Введение новой переменной

Обозначить повторяющееся выражение, содержащее переменную другой буквой.

Записать уравнение, заменив сложные выражения новой переменной.

Решить получившееся уравнение.

Подставить найденные значения переменной в выражение для замены исходной переменной.

Дробно рациональные уравнения

Уравнения, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.

Рациональное уравнение, в котором и левая и правая части являются целыми выражениями, называют целым.

Рациональное уравнение, в котором левая или правая часть является дробным выражением, называют дробным.

Алгоритм решения дробно рациональных уравнений.

Чтобы решить дробно рациональное уравнение, надо:

1) Разложить все знаменатели дробей, входящих в уравнение, на множители.

2) Найти общий знаменатель этих дробей.

3) Умножить все слагаемые данного уравнения на общий знаменатель.

4) Решить получившееся целое уравнение.

5) Из найденных корней исключить те, которые обращают в нуль общий знаменатель данного уравнения.

Источник

Решение простых линейных уравнений

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие уравнения

Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.

В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядит так

ах + b = 0, где a и b — действительные числа. Что поможет в решении: Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа. Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством. Числовой коэффициент — число, которое стоит при неизвестной переменной. Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз: Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем. Как решать простые уравнения Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила. 1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный. Для примера рассмотрим простейшее уравнение: x+3=5 Начнем с того, что в каждом уравнении есть левая и правая часть. Перенесем 3 из левой части в правую и меняем знак на противоположный. Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2. Решим еще один пример: 6x = 5x + 10. Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус. Приведем подобные и завершим решение. 2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок. Применим правило при решении примера: 4x=8. При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение. Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица. Разделим каждую часть на 4. Как это выглядит: Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения: Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12 Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах. Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные. Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки. Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе. А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе. Примеры линейных уравнений Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе! Пример 1. Как правильно решить уравнение: 6х + 1 = 19. Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1. 5х — 15 + 2 = 3х — 2 + 2х — 1 Ответ: х — любое число. Пример 3. Решить: 4х = 1/8. Пример 4. Решить: 4(х + 2) = 6 — 7х. Пример 5. Решить: Пример 6. Как решить линейное уравнение: х + 7 = х + 4. 5х — 15 + 2 = 3х — 2 + 2х — 1 Пример 7. Решить: 2(х + 3) = 5 — 7х.. Источник Об уравнениях высших степеней Как правило в физике, информатике и экономике мы сталкиваемся с простейшими линейными, или дробно-рациональными уравнениями, реже с квадратными. А что до уравнений третьей и четвёртой степени? Если вам интересно, то прошу под кат. Для начала рассмотрим понятие уравнения высшей степени. Уравнением высшей степени, называется уравнение вида: В этой статье я рассмотрю: 1. Кубические уравнения. 2. Возвратные кубические. 3. Применение схемы Горнера и теоремы Безу. 4. Возвратные биквадратные уравнения. Кубические уравнения Кубические уравнения, это уравнения, в которых у неизвестной при старшем члене степень равна 3. Кубические уравнения имеют следующий вид: Решать такие уравнения можно по разному, однако мы воспользуемся знаниями базовой школы, и решим кубическое уравнение методом группировки: В данном примере используется метод группировки, группируем первые два и последние два члена, получая равные скобки, снова выносим, получая уравнение из двух скобок. Произведение равно нулю тогда, и только тогда, если хотя бы один из множителей равен нулю, на основании этого мы каждый множитель (скобку) приравниваем к нулю, получая неполное квадратное и линейное уравнения. Также стоит отметить, что максимальное количество корней уравнения, равно степени неизвестной при главном члене, так в кубическом уравнении может быть не более трёх корней, в биквадратном (4-ой степени) не более четырёх корней и. т. д. Возвратные кубические уравнения Возвратные кубические уравнения имеют вид: Возвратными они называются потому что коэффициенты будут зеркально повторяться. Подобные уравнения тоже решаются школьными методами, но чуть хитрее: Сначала производится группировка, потом при помощи формул сокращённого умножения мы раскладываем получаемое на множители. Снова получаем 2 равные скобки, «выносим их». Получаем два множителя (скобки) и решаем их как два различных уравнения. Теорема Безу и схема Горнера Теорема Безу была открыта, как ни удивительно, Этьеном Безу, французским математиком, занимавшимся в основном алгеброй. Теорему Безу, можно сформулировать следующим образом: Давайте разберёмся. P(x) — это какой-либо многочлен от x, (x — a) — это двучлен в котором a — это один из целых корней уравнения, который мы находим среди делителей свободного члена. Три точки, это оператор обозначающий что одно выражение делится на другое. Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д. Но одно дело понять, а как поделить? Можно конечно, делить и в столбик, однако этот метод доступен далеко не всем, да и вероятность ошибиться очень высока. Поэтому есть и иной путь, это схема Горнера. Её работу я поясню на примере. Предположим: И так, нам дан многочлен, и мы возможно заранее нашли один из корней. Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так: (Картинка позаимствована здесь) Далее поступаем точно так же и с остальными столбцами. Значение последнего столбца (2 строки) будет остатком от деления, в нашем случае 0, если получается число отличное от 0, значит надо избрать другой подход. Пример для кубического уравнения: Возвратные биквадратные уравнения Выше мы так же рассматривали возвратные кубические уравнения, а теперь разберём биквадратные. Их общий вид: В отличие от кубического возвратного уравнения, в биквадратном пары, относительно коэффициентов, есть не у всех, однако в остальном они очень схожи. Вот алгоритм решения таких уравнений: Как видно, решать такие уравнения совсем не просто. Но я всё равно разберу и этот случай. Начинается решение с деления всего уравнения на x^2. Далее мы группируем, здесь я специально ввёл дополнительную строку для ясности. После этого мы совершаем хитрость, и вводим в первую скобку 2, которую мы сначала прибавляем, а после вычитаем, сумма всё равно не изменится, зато теперь мы можем свернуть эту скобку в квадрат суммы. А теперь перейдём к примеру: Основная часть так же как и в обобщённом алгоритме, делим на x^2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x). Область применения В виду своей громоздкости и специфичности уравнения высших степеней редко находят себе применение. Однако примеры всё же есть, уравнение Пуассона для адиабатических процессов в Физике. Источник ← храм в старой некрасовке учетная политика усн и енвд совмещенная образец → Вам также понравится Как построить флай машину в майнкрафте 01.10.202304.09.2023 admin 0 единорог символ чего для женщины 05.10.202319.08.2023 admin 0 Как растянуть тряпочную обувь 04.10.202319.08.2023 admin 0 Добавить комментарий Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.