Как решать трехзначные примеры
Математика
План урока:
Нас ждет много интересного,
И совсем нам неизвестного.
Стараться будем мы решать,
Начнем урок с устного счета, чтобы проверить, насколько вы внимательны, быстро соображаете и много знаете. Образцом для подражания в труде нам послужат крылатые труженицы, вкусные сладкие творения которых известны нам с самого детства.
Посмотрите, в карточке перепутались буквы:
Чтобы прочитать слово, выполните по порядку следующие операции:
1. Найдите значения выражений.
2. Запишите их в порядке уменьшения результатов,
3. Прочитайте название маленьких помощников человека.
Если задание выполнили правильно, то получится слово «пчелы».
Сегодня на уроке узнаете интересные факты из жизни этих необычных насекомых, а также научитесь письменно выполнять умножение и деление в пределах тысячи.
Всю свою недолгую жизнь пчелы не сидят без дела, постоянно работают и приносят нектар с цветущих растений в улей.
В деревянном домике одновременно проживают до сорока тысяч тружениц, каждая из них выполняет свое предназначение. Это огромное количество жужжащих старательных пчелок позволяет получить за сезон десятки килограммов меда.
Решите задачу. Представьте, что три пчелиных семьи заготовили за лето по 178 кг меда. Сколько всего килограммов ценного продукта удалось получить?
Чтобы ответить на вопрос задачи, надо выполнить умножение трехзначного числа 178 на три. Нам трудно посчитать устно, поэтому для решения понадобится знание алгоритма письменного умножения.
Алгоритм письменного умножения трехзначного числа на однозначное число
Давайте вспомним, что такое алгоритм на примере пчел. Жизнь их проходит все в определенной последовательности. Насекомые работают группами и делают все по порядку: пока молодые − хлопочут в улье, более опытные насекомые вылетают на сбор нектара.
Также происходит и в мире людей. Дети с ранних лет привыкают ежедневно выполнять какие-либо дела в определенном порядке. Например, утром вы открываете глаза, потягиваетесь, встаете с кровати, совершаете туалет, занимаетесь зарядкой, завтракаете, собираетесь в школу.
Когда порядок нарушается, получается неожиданный результат, можно опоздать на уроки.
Значит, алгоритм — это последовательность определенных операций друг за другом. Например, любую математическую операцию можно провести столбиком. Умножение столбиком трехзначного числа на однозначное и деление не являются исключениями. Как всегда, надо быть внимательными и не пропускать ни одного шага, иначе выходит неправильный ответ.
В задаче нам нужно умножить 178 на 3. Правила операций будут следующими:
Сначала каждую цифру множителей запишите столбиком. Второй множитель – тройку запишите под разрядом единиц трехзначного числа, то есть под восьмеркой.
Далее начинайте выполнять умножение с единиц. 8 × 3= 24.
Четыре напишите под единицами, а два десятка запомните.
Теперь перемножьте десятки. 7 × 3 = 21. Да два в уме. 21 + 2 = 23.
Три запишите под десятками, а два – запомните.
Перемножьте сотни. 1 × 3 = 3, да два в уме. 3 + 2 = 5.
Прочитайте выражение и ответ. 178 умножить на 3, получится 534.
Напишите ответ в задаче: Три пчелиных семьи за лето приготовили 534 кг меда.
Летние труженицы уверены, что ребята поняли порядок умножения. Поэтому они расскажут про свой «городок», где живут и попросят о помощи.
Чтобы собрать больше меда, на опушке леса люди устраивают пасеку. На цветочной поляне выставляют друг за другом много специальных домиков для каждой пчелиной семьи. Получаются большие улицы, где каждый улей имеет свой номер. Пасечники переходят от домика к домику, ухаживают за каждым роем и собирают урожай.
Решите примеры на умножение столбиком, и подскажите номера пчелиных домиков.
Если у вас получилось верно, то вы прекрасно справились. Молодцы! Значит, без проблем сможете выполнить умножение любого многозначного числа на однозначное.
Продолжаем знакомство с пчелами. Живут труженицы совсем немного − до 40 дней. Одна пчела собирает несколько грамм нектара. Ей необходимо десять миллионов раз слетать от улья к цветку и обратно для того, чтобы получилось 500 г меда. Поэтому они работают все вместе.
Пчелиный рой опыляет девятнадцать миллионов разных цветов, пролетает триста тысяч километров, приносит нектар в соты, чтобы получился 1 кг меда. Миллионы километров потребуется пролететь пчелам, чтобы собрать десятки килограммов ценного продукта. Вот так без устали трудятся маленькие насекомые. Берите с них пример в прилежании, ребята.
Приемы письменного деления в пределах 1000
Решите задачу.
Одна пчела за рабочий день в хорошую погоду посещает примерно 7 тысяч цветков. Сколько дней нужно летать, если надо опылить 875 тысяч цветков, при условии, что погода благоприятная для сбора нектара?
Устно разделить довольно трудно. Важно научиться делению трёхзначных чисел в столбик или уголком. Математики такое название дали по знаку деления. Привычное двоеточие заменили на линии уголком. Как и при умножении, важно строго выполнять последовательность действий.
Вспомните названия компонентов действия деления: делимое делится на делитель, получается частное.
Давайте решим задачу. Будем рассуждать так: чтобы узнать, сколько дней понадобится одной пчелке для сбора нектара, надо все количество цветков разделить на число ежедневного сбора.
875 разделить на 7
Записываем действие столбиком.
При записи справа от делимого провести карандашом вертикальную черту в две клеточки, а затем ровно посередине горизонтальную линию длиной в три клеточки. Черта заменяет знак «получится».
Над чертой посередине запишите делитель, а под ней будем аккуратно записывать результат деления − частное.
Внимательно посмотрите на рисунок. В частном будет три цифры. Почему? Потому что количество сотен 8 делится на частное 7, восьмерка – искомое неполное делимое. Простым карандашом нарисуйте значок:
Последующие две цифры получатся в результате деления десятков и единиц.
Аккуратно поставьте карандашом 3 точки. Так вы запомните, что получится трехзначное число.
7 × 1 = 7. Из неполного делимого отнимите семь. Подчеркните прямой чертой. Выполните вычитание. Получится 1. Запишите в решении под чертой.
Снесите вниз из делимого десятки – 7. Второе неполное делимое равно 17.
В нем делитель 7 помещается два раза. 7 × 2 = 14. В ответе справа от единицы запишите двойку.
Выполните вычитание 17 – 14 = 3. Запишите тройку и снесите последнюю цифру – 5.
Третье неполное делимое равно 35. Оно делится на семь без остатка.
35 : 7 = 5 Пятерку запишите в частное.
Выполните вычитание. 35 − 35 = 0
Остаток нуль. Прочитайте ответ: сто двадцать пять.
Значит нужно 125 дней теплых солнечных дней, чтобы собрать нектар с поляны.
Но лето короткое и рабочие насекомые живут недолго, поэтому пчелы трудятся большими семьями. В течение своей маленькой жизни быстрая пчела никогда не отдыхает и меняет обязанности.
Проследим, кем работает пчела на протяжении своего короткого века.
Малышка после рождения шесть дней скребет соты для поселения личинок и укладки нектара. Она поддерживает чистоту сот, чтобы уберечь семью от вирусов.
В возрасте от 6 до 12 дней пчелка исполняет роль воспитателя. Она кормит личинок и матку. Поит молочком, согревает мохнатым телом.
К концу второй недели повзрослевшее насекомое строит из воска соты, налаживает старые стенки. «Строители» забирают нектар у собирателей, ароматную пыльцу, добавляют капельку меда, утрамбовывают в новенькие ячейки.
В возрасте 21 дня насекомые охраняют леток от незваных гостей и ленивых, которые прилетели без урожая. Скрывать нечего − встречаются пчелы-трутни.
Повторите алгоритм деления трехзначного на однозначное число.
Узнайте возраст «сборщиц» даров лесной опушки получите, выполнив пример на деление 234 : 9. Возьмите ручку и карандаш запишите решение уголком в тетради.
Определите первое неполное делимое и количество цифр в частном. Рассуждайте так: в разряде сотен – двойка. Два разделить на девять не сможем. 2 1 664
Как решать трехзначные примеры
Сколько примеров создать? Придумать √ 50 | 100 | 200 | 300 | 400 | 500 примеров
По сколько столбцов отображать примеры? Печатать в √ 2 | 3 | 4 столбца
Создано примеров на для тренировки арифметических действий: 0
Примеры на с ответами:
Сгенерировано примеров на с ответами в качестве тренажера по математике: 0
Не удалось сгенерировать 50 примеров на с ответами, т.к. это принципиально невозможно для исходных условий задачи.
 Скачать |  Распечатать |
На этой странице сайта результат работы генератора случайных примеров по математике на для тренировки арифметических действий учениками 1, 2, 3, 4 классов средней общеобразовательной школы.
Тренировочные примеры по математике на для учеников первого, второго, третьего, четвертого класса можно отображать для распечатки или скачивания в два, три или четыре столбца.
Для более оперативной связи пишите мне в ICQ (аську): 82079833 (Ник Raman) или в Skype: логин RamanKursk.
Я часто бываю в Интернет онлайн.
Обратите внимание: Любой молодой специалист без опыта работы хочет найти хорошую работу с достойной оплатой. Мы рекомендуем для поиска работы использовать сайт-агрегатор объявлений с вакансиями России, СНГ, ЕАЭС Rabotka.com.ru.
Copyright © 2018-2021 Software and design by Raman
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
На уроке познакомимся с делением на трехзначное число столбиком с остатком и без остатка, будем решать задачи с единицами площади, устроим небольшое соревнование на присуждения звания «Знаток математики».
Начнем урок с разминки. Проверим, как вы знаете табличное деление! Ведь без знаний таблицы умножения и деления невозможно научиться делить столбиком на трехзначное число.
Примеры списывать не нужно. Записывайте только ответы в 4 столбика.
Проверь себя.
Оцените свои достижения.
Письменное деление на трехзначное число
Ребята, как вы думаете, отличается ли алгоритм деления на трехзначное число от знакомого нам алгоритма на двузначное число?
Нет, не отличается! Давайте повторим последовательность наших действий при делении столбиком.
Используя данный алгоритм, решим вместе несколько примеров. Будем делать записи в черновике. Вы знаете, что цифры в частном – пробные, и требуется проверка.
984 : 123 1 155 : 9 318 : 106 5 850 : 9
Оставшиеся примеры на деление решите самостоятельно. Проверьте себя по образцу.
Проверь себя.
При делении многозначных чисел столбиком ребята часто пропускают нули в частном. Обидная ошибка! Как этого не допустить? Рассмотрим более сложные случаи деления, когда в частном появляются нули.
Есть маленькие секреты безошибочного деления столбиком!
А теперь решите самостоятельно пример. Подумайте, нужен ли нуль в частном. Сравните свое решение с образцом.
55 692 : 273
Проверь себя.
Деление на трехзначное число с остатком
Вспомним главное правило при делении с остатком.
Это правило применимо для деления на любое число (одно-, двух-, трехзначное и т.д.).
Ребята, перед вами тетрадь ученика 4 класса. Проверьте, как выполнено деление на трехзначное число с остатком. Решите эти примеры в своем черновике. Сравните. Оцените работу четвероклассника.
Во втором примере остаток 148 больше делителя 125. Как вы думаете, почему так получилось? Пробная цифра 2 не подходит. В частном должна быть цифра 3. Умножим 125 на 3. Получим 375. Остаток 23 меньше делителя 125.
А вот первый пример решен верно. Оставим его без изменений. Во втором примере исправим ошибку.
Решение задач с единицами площади
Ребята, взрослые люди часто испытывают досаду, занимаясь ремонтом дома или квартиры. Почему? Знакома ситуация, когда чуть-чуть не хватило краски или обоев? Нужно срочно бежать в магазин, чтобы купить недостающие материалы. Можно ли этого избежать? Конечно, можно! Главное, правильно выполнить расчеты. Например, правильно измерить площадь пола под покраску или площадь стен под обои.
Задача
В комнате длиной 7 м и шириной 8 м укладывают на пол ламинат квадратами 50х50 см. Сколько штук ламината потребуется для этой комнаты?
Подсказка. Вычислите площадь комнаты и площадь одного квадрата ламината. Одинаковые ли единицы площади вы использовали? Выразите квадратные метры в квадратных сантиметрах.
Решите задачу самостоятельно.
Проверь себя.
S пола = 7 ∙ 8 = 56 (м²)
S лам. = 50 ∙50 = 2 500 (см²)
10 000 : 2 500 = 4 (шт.) – ламината в 1 м².
56 ∙ 4 = 224 (шт.) – ламината потребуется.
Ответ: 224 штук ламината.
Задача
Для покраски пола комнаты площадью 35 м² купили 3 кг краски. Хватит ли этой краски, если на 1 м² пола расходуется 100 г краски.
Выразим 3 кг в граммах.
35 ∙ 100 = 3 500 (г) – краски потребуется.
3 500 – 3000 = 500 (г) – краски не хватит для покраски пола.
Ответ: 500 г краски не хватит.
Решите аналогичную задачу самостоятельно и проверьте по образцу.
Задача
Стены комнаты решили оклеить обоями. Площадь поверхности составляет 80 м². На одной стене есть окно – 3 м², а на другой – дверь занимает 4 м². Хватит ли 7 рулонов обоев, если в одном рулоне 10 м² обоев.
Проверь себя.
3 + 4 = 7 (м²) – занимают окно и дверь.
80 – 7 = 73 (м²) – нужно оклеить обоями.
7 ∙ 10 = 70 (м²) – в семи рулонах.
73 – 70 = 3 (м²) – обоев не хватит.
Ответ: не хватит 3 м².
Ребята, на уроке мы учились делить на трехзначное число без остатка и с остатком, решали сложные задачи с единицами площади. А теперь настало время подвести итоги! Устроим небольшое соревнование на звание «Знатока математики».
Решите примеры за одну минуту!
(12 543 – 3 890 + 15 498) ∙ 69 ∙ 0 ∙594 =
640 ∙5 ∙0 +640 : 1 – 630 =
? + 150 – 240 – 10 + 26 = 526
Проверь себя.
Кому удалось справиться с заданием за одну минуту, может смело назвать себя большим молодцом!
В первом и втором выражениях самые наблюдательные заметили умножение на нуль (можно не вычислять все выражение, а ∙ 0 = 0).
В третьем выражении первое число можно быстро найти, вычисляя с конца обратным действием: 526 – 26 + 10 + 240 – 150 = 600
Вычитание столбиком
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.
Название числа напрямую зависит от количества знаков. Однозначное — состоит из одного знака. Двузначное — из двух. Трехзначное — из трех и так далее.
Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.
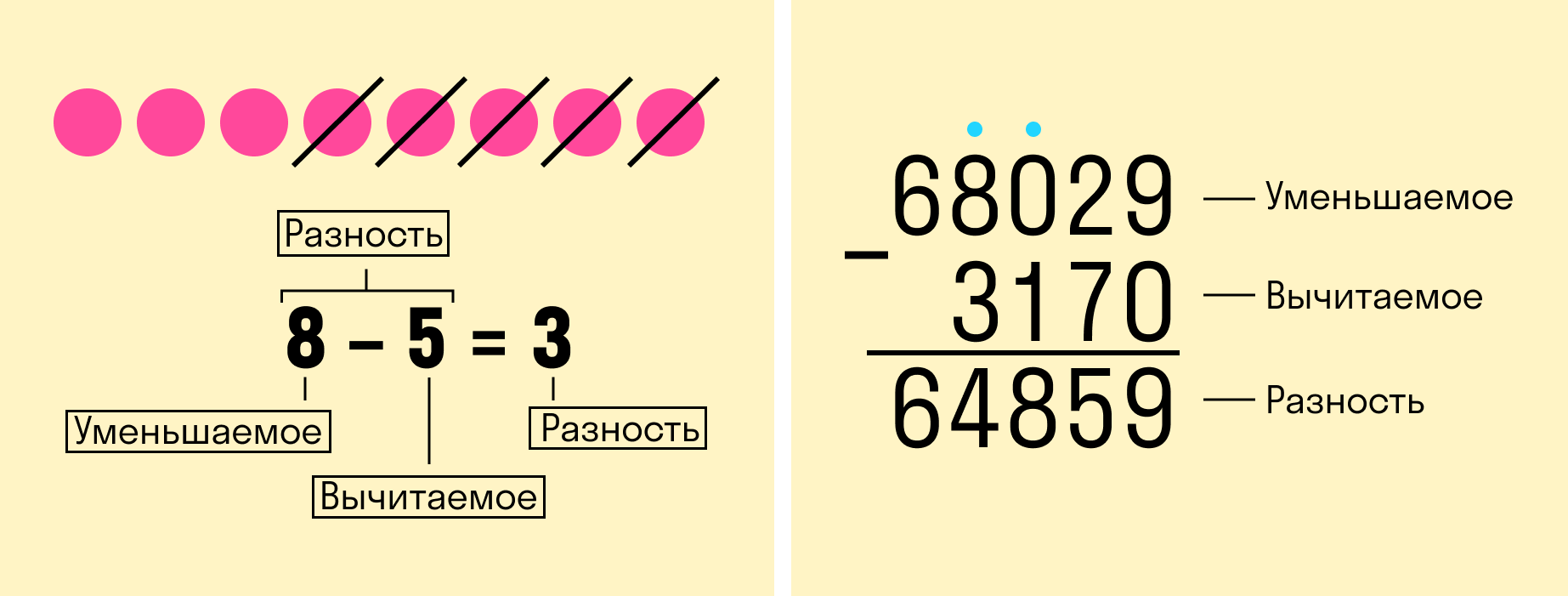
Вычитание — это арифметическое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее — вычитаемым. Результат их вычитания — разностью.