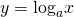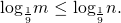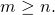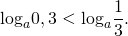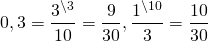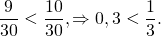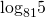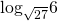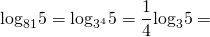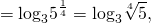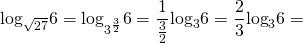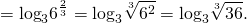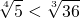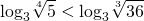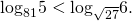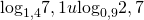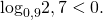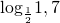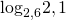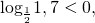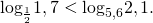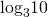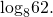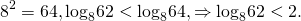Как решать сравнение логарифмов

Сравнение логарифмов

Ни для кого не секрет, что с помощью применения логарифмов мы упрощаем довольно много сложных алгебраических операций и не только. Логарифмы дают возможность заменять более сложные операции умножения на операции сложения, деление на вычитание. Согласитесь, ведь это намного проще. Если уже быть совсем точными, то логарифм заданного числа – это показатель степени, в которую нужно возвести другое, также заданное число, чтобы получить данное. На первый взгляд все запутано и непонятно, но это только на первый, на самом деле, все до нельзя просто. Для того, чтобы закреплять знания о логарифмах (да и не только о них), конечно же, рекомендовано после прочтения теории выполнять самостоятельные практические упражнения, это не только поможет усвоить материал, но и выявить все недочеты.

Но вернемся к логарифмам, а точнее к их сравнению. Разумеется, вам в голову может прийти вопрос: «что такое сравнение логарифмов? и как это делается?».

Зачем мы сравниваем логарифмы? Ответ достаточно прост. При решении неравенств и уравнений, довольно часто возникает вопрос, когда нужно определить принадлежность корня области допустимых значений или же сделать соотношение решений двух или более неравенств на числовой прямой, а решение, при этом, выражается иррациональным числом, которое, в свою очередь, записано с помощью логарифма. Вот тут-то нам и необходимо сравнение этих логарифмов.

Существуют несколько способов сравнения логарифмов. Какой из них использовать зависит, в первую очередь, от того, одинаковые основания у логарифмов или нет. Если первый вариант, то тут выход один – использовать монотонность логарифмических функций.

Если числа равные, но основания разные, то тут можно пойти несколькими путями:

Источник

Приемы и методы сравнения логарифмов

Разделы: Математика

Сравнение значений логарифмов или значения логарифма с некоторым числом встречается в школьной практике решения задач не только как самостоятельная задача. Сравнивать логарифмы приходится, например, при решении уравнений и неравенств. Материалы статьи (задачи и их решения) располагаются по принципу “от простого к сложному” и могут быть использованы для подготовки и проведения урока (уроков) по данной теме, а также на факультативных занятиях. Количество рассматриваемых задач на уроке зависит от уровня класса, его профильного направления. В классах с углубленным изучением математики этот материал может быть использован для двухчасового урока-лекции.

1. (Устно.) Какие из функций являются возрастающими, а какие убывающими:

Замечание. Это упражнение является подготовительным.

Замечание. При решении упражнения № 2 можно использовать как свойства логарифмической функции с привлечением графика логарифмической функции, так и следующее полезное свойство:

Положительные числа и 10 (основание логарифма) лежат по разные стороны от 1. Значит, a >1, то при b>1 справедливо неравенство log_ab > log_cb.

Так как 1 1, то log₅13 > log₇13.

5. Сравните числа log₂6 и 2.

Первый способ (использование монотонности логарифмической функции).

Второй способ (составление разности).

Составим разность .

-1 = ;

7. Сравните числа и 3log₈26.

Функция y = log₂t возрастает на R₊, 25 25. Значит,

Составим разность
. Отсюда .

Оценим логарифмы, учитывая, что функции y = log₄t и y = log₆t возрастающие на R₊:

Учитывая, что функции убывающие на R₊, имеем:

. Значит,

Замечание. Предложенный метод сравнения называют методом “вставки” или методом “разделения” (мы нашли число 4, разделяющее данные два числа).

Заметим, что оба логарифма больше 1, но меньше 2.

Первый способ. Попробуем применить метод “разделения”. Сравним логарифмы с числом .

Второй способ (умножение на натуральное число).

Замечание 1. Суть метода “умножения на натуральное число” в том, что мы ищем натуральное число k, при умножении на которое сравниваемых чисел a и b получают такие числа ka и kb, что между ними находится хотя бы одно целое число.

Замечание 2. Реализация вышеописанного метода бывает весьма трудоемка, если сравниваемые числа очень близки друг к другу.
В этом случае можно попробовать сравнение методом “вычитания единицы”. Покажем его на следующем примере.

Первый способ (вычитание единицы).

Вычтем из сравниваемых чисел по 1.

В первом неравенстве мы воспользовались тем, что

если c > a > 1, то при b > 1 справедливо неравенство log_ab > log_cb.

Во втором неравенстве – монотонностью функции y = log_ax.

Замечание. Вычитать из сравниваемых чисел можно любое натуральное число n. При этом часто бывает достаточно взять n = 1.

Второй способ (применение неравенства Коши).

Получаем неравенство .

Найдем множество решений неравенства , удовлетворяющих условию x > 0.

Возведем обе части неравенства в квадрат (при x > 0 обе части неравенства положительны). Имеем 9x 2 0, получаем: .

Ответ: неравенство верно.

Практикум по решению задач.

2. Расположите в порядке возрастания числа:

Методов сравнения логарифмов много. Цель уроков по данной теме – научить ориентироваться в многообразии методов, выбирать и применять наиболее рациональный способ решения в каждой конкретной ситуации.

В классах с углубленным изучением математики материал по данной теме может быть изложен в форме лекции. Такая форма учебной деятельности предполагает, что материал лекции должен быть тщательно отобран, проработан, выстроен в определенной логической последовательности. Записи, которые делает учитель на доске, должны быть продуманными, математически точными.

Закрепление лекционного материала, отработку навыков по решению задач целесообразно проводить на уроках-практикумах. Цель практикума – не только закрепить и проверить полученные знания, но и пополнить их. Поэтому задания должны содержать задачи разного уровня, от самых простых задач до задач повышенной сложности. Учитель на таких практикумах выступает в роли консультанта.

Источник

Как сравнивать логарифмы

Как сравнивать логарифмы?

При сравнении логарифмов используют свойства логарифмической функции

При сравнении логарифмов с одинаковыми основаниями :

— если основание больше единицы (a>1), функция возрастает, значит, большему значению аргумента соответствует большее значение функции (то есть знак неравенства не изменяется);

— если основание меньше единицы (0

С помощью схемы сравнение логарифмов можно изобразить так:

1) Сравнить b и c, если

<\log _3>c.\]» title=»Rendered by QuickLaTeX.com»/>

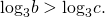
Основание 3>1, функция возрастает, знак неравенства между выражениями, стоящими под знаками логарифмов, не изменяется:

c.\]» title=»Rendered by QuickLaTeX.com»/>

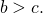
2) Сравнить m и n, если

Основание 1/9

3) Сравнить с единицей основание логарифма, если

Сравним числа, стоящие под знаками логарифмов. Для этого представим их в виде обыкновенных дробей с одинаковыми знаменателями:

То есть, знак неравенства не изменился. Значит, функция возрастает и основание a>1.

Сравнение логарифмов с разными основаниями.

Чтобы сравнить логарифмы с разными основаниями, можно попытаться, используя свойства логарифмов, привести их к одинаковым основаниям.

Оба логарифма можно привести к основанию 3:

и основание 3>1, функция возрастает и знак неравенства не изменяется:

Иногда бывает достаточно сравнить логарифмы с нулём.

Сравним каждый из логарифмов с нулём:

0,\]» title=»Rendered by QuickLaTeX.com»/>

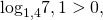
Так как первый логарифм больше нуля, а второй — меньше нуля, то

<\log _<0,9>>2,7\]» title=»Rendered by QuickLaTeX.com»/>

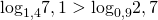
Сравниваем каждый из логарифмов с нулём:

0\]» title=»Rendered by QuickLaTeX.com»/>

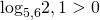
Первый логарифм меньше нуля, второй — больше нуля, следовательно, первый логарифм меньше второго:

Сравнивать логарифмы можно, опираясь непосредственно на определение логарифма.

<\log _3>9, \Rightarrow <\log _3>10 > 2;\]» title=»Rendered by QuickLaTeX.com»/>

<\log _8>62.\]» title=»Rendered by QuickLaTeX.com»/>

Источник

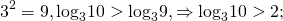
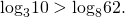
Логарифмические неравенства и системы

п.1. Методы решения логарифмических неравенств

При решении логарифмических неравенств используются следующие основные методы:
1) переход от логарифмического неравенства к равносильному неравенству между \(f(x)=g(x)\) с системой неравенств, описывающих ОДЗ;
2) графический метод;
3) замена переменной.

п.2. Решение неравенств вида \(\log_a f(x)\gt\log_a g(x)\)

Если \(a\gt 1\), логарифмическое неравенство \(\log_a f(x)\gt\log_a g(x)\) равносильно системе: \begin \log_a f(x)\lt\log_a g(x) \Leftrightarrow \begin f(x)\gt g(x)\\ f(x)\gt 0\\ g(x)\gt 0 \end \end Знак неравенства между \(f(x)\) и \(g(x)\) сохраняется.

Если \(0\lt a\lt 1\), логарифмическое неравенство \(\log_a f(x)\gt\log_a g(x)\) равносильно системе: \begin \log_a f(x)\lt\log_a g(x) \Leftrightarrow \begin f(x)\lt g(x)\\ f(x)\gt 0\\ g(x)\gt 0 \end \end Знак неравенства между \(f(x)\) и \(g(x)\) меняется на противоположный.

Неравенства \( \begin f(x)\gt 0\\ g(x)\gt 0 \end \) в системе соответствуют ограничению ОДЗ для аргумента логарифмической функции.

Например:
Решим неравенство \(\log_2(3x-1)\gt\log_2(2-5x)\)
\begin \log_2(3x-1)\gt\log_2(2-5x)\Leftrightarrow \begin 3x-1\gt 2-5x\\ 3x-1\gt 0\\ 2-5x=\gt 0 \end \\ \begin 8x\gt 3\\ 3x\gt 1\\ 5x\lt 2 \end \Rightarrow \begin x\gt\frac38\\ x\gt\frac13\\ x\lt\frac25 \end \Rightarrow\frac38\lt x\lt \frac25 \end Ответ: \(x\in\left(\frac38;\frac25\right)\)

Система \( \begin f(x)\gt g(x)\\ f(x)\gt 0\\ g(x)\gt 0 \end \Leftrightarrow \begin f(x)\gt g(x)\\ g(x)\gt 0 \end \Leftrightarrow f(x)\gt g(x)\gt 0 \)
т.е., можно опустить второе неравенство.
Система \( \begin f(x)\lt g(x)\\ f(x)\gt 0\\ g(x)\gt 0 \end \Leftrightarrow \begin f(x)\lt g(x)\\ f(x)\gt 0 \end \Leftrightarrow 0\lt f(x)\lt g(x) \)
т.е., можно опустить третье неравенство.
Научитесь отбрасывать лишнее неравенство: при решении сложных систем этот навык очень пригодится.

п.3. Решение неравенств вида \(\log_ f(x)\gt \log_ g(x)\)

п.4. Сравнение логарифмов с разными основаниями от одного аргумента

Для \(\log_a x\) и \(\log_bx\) с разными основаниями и одним аргументом справедливы следующие соотношения:

\(a\gt b\gt 1\)	\(1\gt a\gt b\gt 0\)
\begin \log_bx\gt\log_ax,\ \ x\in(1;+\infty)\\ \log_bx\lt\log_ax,\ \ x\in(0;1) \end	\begin \log_bx\gt\log_ax,\ \ x\in(1;+\infty)\\ \log_bx\lt\log_ax,\ \ x\in(0;1) \end

п.5. Примеры

Пример 1. Сравните числа:
a) \( a=\log_5\frac78,\ b=\log_6\frac78 \)
Аналитический метод:
\begin a=\frac<\lg\frac78><\lg 5>=\frac<\lg 7-\lg 8><\lg 5>\lt 0,\ \ b=\frac<\lg\frac78><\lg 6>=\frac<\lg 7-\lg 8><\lg 6>\lt 0\\ a-b=\frac<\lg 7-\lg 8><\lg 5>-\frac<\lg 7\lg 8><\lg 6>=(\lg 7-\lg 8)\left(\frac<1><\lg 5>-\frac<1><\lg 6>\right)\\ a-b=\frac<\overbrace<(\lg 7-\lg8)>^<\lt 0>\overbrace<(\lg 6-\lg 5)>^<\gt 0>><\underbrace<\lg 5\cdot\lg 6>_<\gt 0>>\lt 0\\ a\lt b \end Графический метод:
\(0\lt\frac78\lt 1\)

При \(0\lt x\lt 1\) кривая \(\log_6x\gt\log_5x\)
Значит, \(b\gt a\)

б) \( a=\log_5 11,\ b=\log_6 11 \)
Аналитический метод:
\begin a=\frac<\lg 11><\lg 5>,\ \ b=\frac<\lg 11><\lg 6>\\ a-b=\lg 11\left(\frac<1><\lg 5>-\frac<1><\lg 6>\right)= \frac<\overbrace<\lg 11>^<\gt 0>\overbrace<(\lg 6-\lg 5)>^<\gt 0>><\underbrace<\lg 5\cdot\lg 6>_<\gt 0>>\gt 0\\ a\gt b \end Графический метод:
\(11\gt 1\)

При \(x\gt 1\) кривая \(\log_5x\gt\log_6x\)
Значит, \(a\gt b\)

Пример 2*. Решите неравенство:
a) \( \log_<0,5>(x^2-7x)\geq\log_<0,5>(3x+11) \) \begin \begin x^2-7x\leq 3x+11\\ x^2-7x\gt 0\\ 3x+11\gt 0 \end \Rightarrow 0\lt x^2-7x\leq 3x+11 \Rightarrow \begin x^2-7x\leq 3x+11\\ x^2-7x\gt \end \Rightarrow \\ \Rightarrow \begin x^2-10x-11\leq 0\\ x(x-7)\gt 0 \end \Rightarrow \begin (x+1)(x-11)\leq 0\\ x(x-7)\gt 0 \end \end
\(-1\leq x\leq 0\cup 7\lt x\leq 11\)
Ответ: \(x\in\left.\left[-1;0\right.\right)\cup\left.\left(7;11\right.\right]\)

б) \( \log_3x+\log_3(x-8)\geq 2 \) \begin \log_3\left(x(x-8)\right)\geq \log_39\\ \begin x(x-8)\geq 9\\ x\gt 0\\ x-8\gt 0 \end \Rightarrow \begin x^2-8x-9\geq 0\\ x\gt 0\\ x\gt 8 \end \Rightarrow \begin (x+1)(x-9)\geq 0\\ x\gt 8 \end \end
\(8\lt x\leq 9\)
Ответ: \(x\in\left.\left(8;9\right.\right]\)

e) \( 4-x\lt\log_2(6+2^x) \)
Перейдем к показательному неравенству: \(2^<4-x>\lt 2^<\log_2(6+2^x)>\)
Получаем:\( \begin 2^<4-x>\lt 6+2^x\\ 6+2^x\gt 0 \end \)
Требование ОДЗ \(6+2^x\gt 0\) выполняется при любом \(x\in\mathbb\)
Решаем основное неравенство: \(\frac<2^4><2^x>\lt 6+2^x\)
Замена: \(t=2^x\gt 0\) \begin \begin \frac<16>-6-t\lt 0\\ t\gt 0 \end \Rightarrow \begin \frac<16-6t-t^2>\lt 0\\ t\gt 0 \end \Rightarrow \begin \frac\gt 0\\ t\gt 0 \end \Rightarrow\\ \Rightarrow \begin t^2+6t-16\gt 0\\ t\gt 0 \end \Rightarrow \begin (t+8)(t-2)\gt 0\\ t\gt 0 \end \end
\(t\gt 2\)
Возвращаемся к исходной переменной: \(2^x\gt 2\Rightarrow x\gt 1\)
Ответ: \(x\in(1;+\infty)\)

Пример 3*. Решите неравенство:
a) \( \log_<\frac1x>7\gt\log_<\frac<1><2x-1>>7 \)
Если оба логарифма одного знака и 7>1, основание справа должно быть больше: \begin \begin \frac<1><2x-1>\gt\frac1x\\ x\gt 0,\ x\ne 1\\ 2x-1\gt 0,2x-1\ne 1 \end \Rightarrow \begin x\gt 2x-1\gt 0\\ x\ne 1 \end \Rightarrow \begin x\gt 2x-1\\ 2x\gt 1\\ x\ne 1 \end \Rightarrow \begin x\lt 1\\ x\gt\frac12\\ x\ne 1 \end \Rightarrow \\ \Rightarrow \frac12\lt x\lt 1 \end Если логарифмы разных знаков, то: \begin \begin \log_<\frac17>\gt 0\\ \log_<\frac<1><2x-1>>7\lt 0 \end \Rightarrow \begin \log_7\frac1x\gt 0\\ x\ne 1\\ \log_7\frac<1><2x-1>\lt 0\\ 2x-1\ne 1 \end \Rightarrow \begin \frac1x\gt 1\\ 0\lt\frac<1><2x-1>\lt 1 \end \Rightarrow \begin x\lt 1\\ 2x-1\gt 1 \end \Rightarrow \begin x\lt 1\\ x\gt 1 \end \Rightarrow \varnothing \end Существует только решение для одинаковых знаков.
Ответ: \(x\in\left(\frac12; 1\right)\)

г) \( \log_2x\cdot \log_3 2x+\log_3x\cdot\log_2 3x\geq 0 \)
ОДЗ: \(x\gt 0\)

в) \( \begin \log_<\sqrt<5>>\sqrt\leq 0\\ \left(\frac12\right)^<1-4x>\gt 32 \end \)
Здесь важно не потерять модуль: \(\sqrt=\sqrt<(x-3)^2>=|x-3|\)
ОДЗ: \(|x-3|\gt 0\Rightarrow x\ne 3\) \begin \begin \log_<\sqrt<5>>|x-3|\leq 0\\ 2^<-1(1-4x)>\gt 2^5 \end \Rightarrow \begin |x-3|\leq 1\\ 4x\gt 6\\ x\ne 3 \end \Rightarrow \begin -1\leq x-3\leq 1\\ x\gt 1,5\\ x\ne 3 \end \Rightarrow \begin 2\leq x\leq 4\\ x\gt 1,5\\ x\ne 3 \end \Rightarrow\\ \Rightarrow 2\leq x\lt 3\cup 3\lt x\leq 4 \endОтвет: \(x\in\left.\left[2;3\right.\right)\cup \left.\left(3;4\right.\right]\)

Источник