Как решать способом группировки
Способ группировки
Кроме вынесения общего множителя за скобки существует еще один способ разложения многочлена на множители — способ группировки.
Этот способ разложения на множители считается более сложным, поэтому перед его изучением, убедитесь, что вы уверенно выносите общий множитель за скобки.
Чтобы разложить многочлен на множители способом группировки, необходимо сделать следующее.
Рассмотрим пример разложения многочлена на множители способом группировки.
Примеры способа группировки
Рассмотрим пример. Требуется разложить многочлен на множители, используя способ группировки.
Первый способ
Обратим внимание, что в двух одночленах повторяется « y 2 » и « z 2 ». Подчеркнем повторяющиеся одночлены и запишем их друг за другом. Затем вынесем общий множитель у каждой группы одночленов.
48x z 2 + 32x y 2 − 15 z 2 − 10 y 2 = 48x z 2 − 15 z 2 + 32x y 2 − 10 y 2 = 3z 2 (16x − 5) + 2y 2 (16x − 5) =
= (16x − 5)(3z 2 + 2y 2 )
Второй способ
Запишем пример еще раз. Теперь обратим внимание, что в первых двух одночленах повторяется « x ». Подчеркнем повторяющиеся одночлены. Вынесем общий множитель у каждой группы одночленов.
48 x z 2 + 32 x y 2 − 15z 2 − 10y 2 = 16x(3z 2 + 2y 2 ) − 5(3z 2 + 2y 2 ) = (3z 2 + 2y 2 )(16x − 5)
В итоге получился такой же ответ, как и при первом способе.
Рассмотрим еще один пример разложения многочлена способом группировки.
Смена знаков в скобках
Иногда для вынесения общего многочлена требуется сменить все знаки одночленов в скобках на противоположные.
Для этого за скобки выносится знак « − », а в скобках у всех одночленов меняются знаки на противоположные.
2ab 2 − 3x + 1 = −( − 2ab 2 + 3x − 1)
Рассмотрим пример способа группировки, где для вынесения общего многочлена, нам потрубуется выполнить смену знаков в скобках.
Способ группировки
Способ группировке в алгебре — один из способов разложения многочлена на множители.
Способ группировки можно разбить на два этапа:
1) Объединение членов многочлена в группы, имеющие общий множитель, и вынесение из каждой группы общего множителя (в одной из групп общего множителя может не быть).
2) Вынесение полученного общего для всех групп множителя за скобки.
Группируем первое слагаемое со вторым, третье — с четвертым.
Лучше при группировке между скобками всегда ставить знак «+»:
Общий множитель (x+7) выносим за скобки:
Группировать можно было иначе: первое слагаемое — с третьим, второе — с четвертым:
Из первых скобок выносим общий множитель x, из вторых — 7:
Общий множитель (a-3) выносим за скобки:
При любом способе группировки ответ получается одинаковый (от перестановки мест множителей произведение не меняется).
Группируем первое слагаемое со вторым, третье — с четвертым:
Из первых скобок выносим общий множитель x, из вторых — «-«:
Общий множитель (4-y) выносим за скобки:
Сгруппируем первое слагаемое со вторым и третьим, четвертое — с пятым и шестым:
Общий множитель (a²+1+b²) выносим за скобки:
Можно было группировать и по два слагаемых. Например, первое — с четвертым, второе — с пятым, третье — с шестым:
Из первых скобок выносим общий множитель a², во вторых скобках общего множителя нет, из третьих — b²:
Общий множитель (a-b) выносим за скобки. Не забываем поставить единицу на место (a-b)!
Разложение многочлена способом группировки
Основные понятия
Мы знаем, что слово «множитель» происходит от слова «умножать».
Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.
Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:
Так выглядит пошаговое разложение на множители. Числа, которые подчеркнуты на картинке — это множители, которые дальше разложить уже нельзя.
Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
5 способов разложения многочлена на множители
Способ группировки множителей
Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.
Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.
Разложить на множители методом группировки можно в три этапа:
Объединить члены многочлена в группы можно по-разному. И ее всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.
Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.
Заметим, что в первой группе повторяется p, а во второй — d.
Вынесем в первой группе общий множитель p, а во второй общий множитель d.
Вынесем его за скобки:
Группировка множителей выполнена.
Заметим, что в первой группе повторяется u, а во второй — b.
Вынесем в первой группе общий множитель u, а во второй общий множитель b.
Заметим, что общий множитель (p + d).
Вынесем его за скобки:
Группировка множителей выполнена.
От перестановки мест слагаемых сумма не меняется, поэтому оба ответа верны:
Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.
Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.
Проверим как это на следующем примере.
Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Решение уравнения методами группировки и замены переменной
Страницы работы
Содержание работы
Лабораторная работа №1
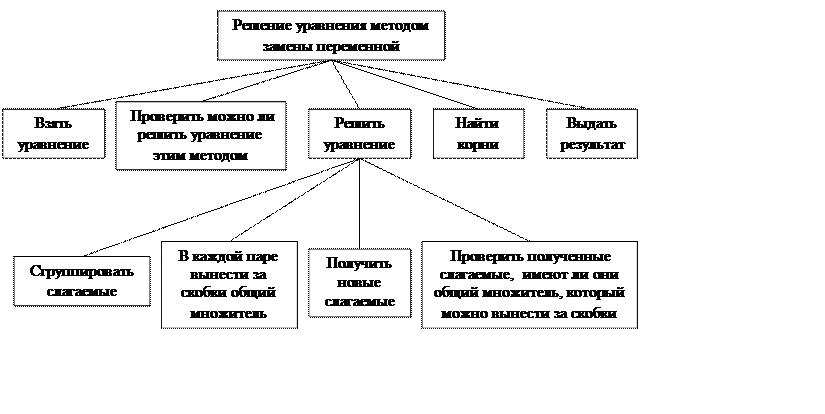
Цель работы: Решить уравнения методами:
б) замены переменной.
Теоретическая часть работы
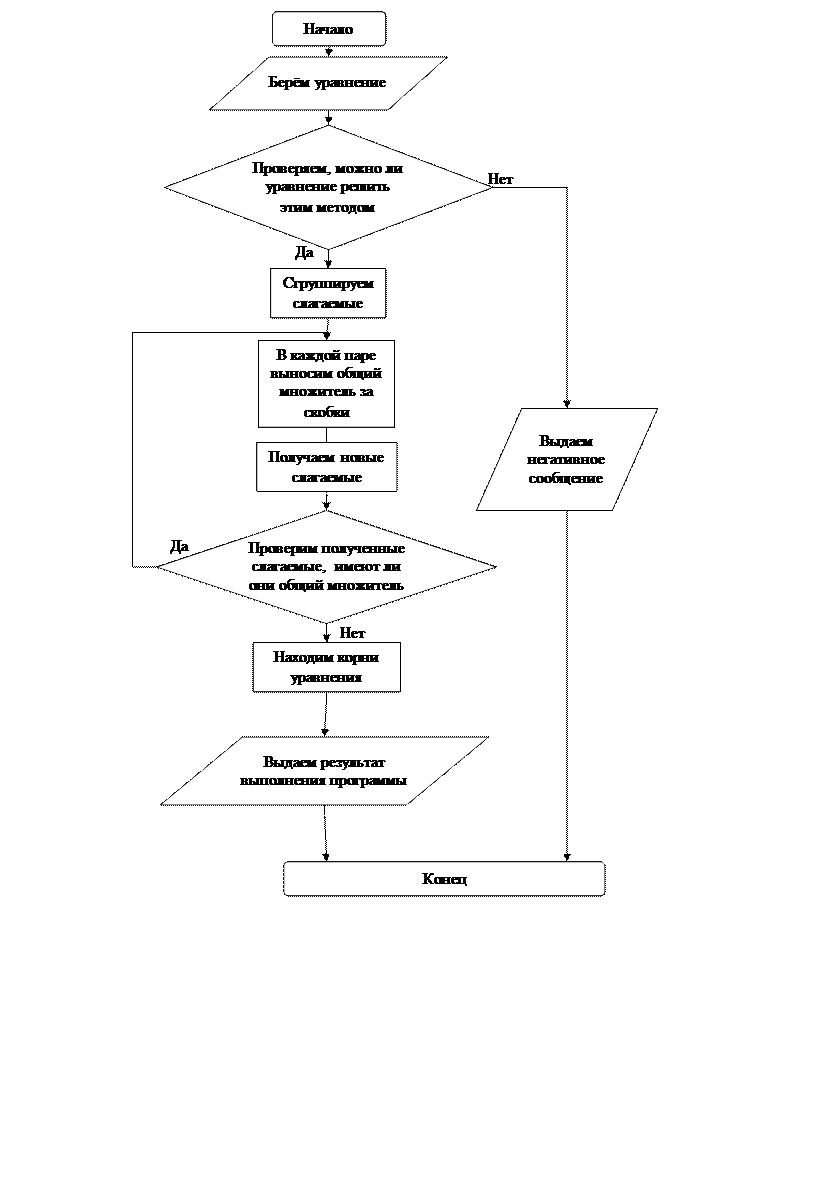
Способ группировки разложение на множители
Для того, чтобы разложить многочлен 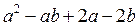
2 – В каждой паре вынесем за скобки общий множитель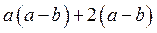
3 – Заметим, что оба полученных слагаемых также имеют общий множитель, который можно вынести за скобки 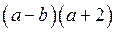
Не любая группировка приводит к разложению на множители. В случае неудачи попробуйте сгруппировать по-другому, или вообще попытайтесь применить другой метод.
Рассмотрим решение уравнения способом разложения на множители на конкретном примере:
Применив способ группировки, получим:
Помня, что произведение равно 0 в случае, если один из множителей равен 0, получим корни уравнения:
Метод введения новой переменной
Пример.
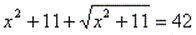
Если уравнение можно свести к уравнению, содержащему два или несколько одинаковых выражений, то это уравнение можно решить методом замены переменной. Для этого заменяют такое выражение другой переменной, получают новое уравнение относительно новой переменной, решают его, затем осуществляют обратную замену, возвращаясь к прежней переменной.
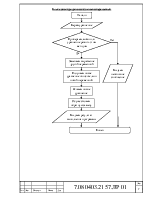
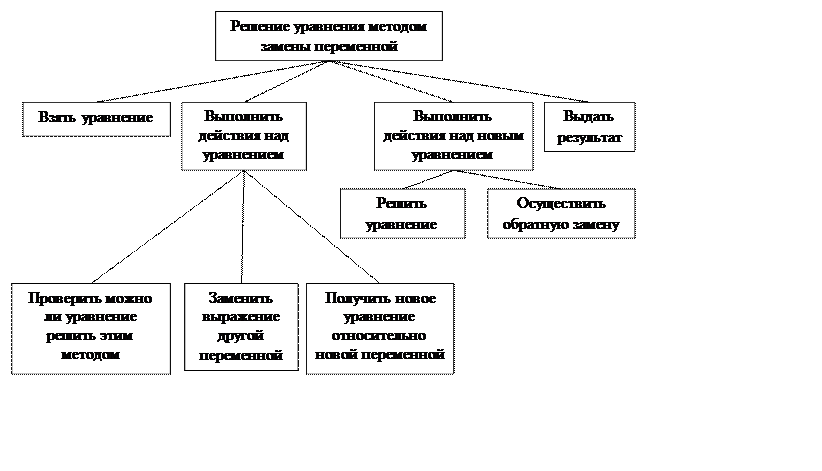
Структурная схема программы: а) способ группировки разложение на множители
Блок-схема программы: а) способ группировки разложение на множители
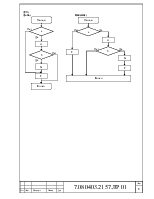
Структурная схема программы: б) замены переменной
Блок-схема программы: б) замены переменной
Группировка слагаемых и множителей: правило, примеры
В случае, если нам надо сложить три и более слагаемых, мы можем использовать метод тождественного преобразования, получивший название группировки слагаемых. Точно такой же метод существует и для умножения, если в примере заданы три множителя и больше. Целью этой статьи является разбор правил группировки в обоих случаях. Все теоретические положения будут проиллюстрированы примерами решений задач.
Что такое группировка слагаемых
Мы можем выполнять группировку как в буквенных, так и в числовых выражениях тогда, когда у нас есть 3 слагаемых и более. Как нужно понимать этот термин?
Группировка слагаемых основана на совместном рассмотрении нескольких слагаемых в исходной сумме. Иначе говоря, это объединение нескольких слагаемых в одну группу.
Основное правило группировки слагаемых звучит так:
При выполнении группировки мы сначала переставляем слагаемые в исходной сумме таким образом, чтобы слагаемые одной группы были рядом, после чего заключаем их в скобки.
На чем базируется данное правило? В его основе лежат переместительное и сочетательное свойство сложения.
Разберем несколько примеров.
Возьмем пример чуть сложнее.
В целом группировка слагаемых– несложное действие. Некоторая трудность может быть в том, чтобы найти в исходном выражении саму сумму и отдельные слагаемые, из которых она состоит, особенно если выражение длинное и громоздкое. После нахождения слагаемых сгруппировать их будет легко.
После нахождения всех элементов можно объединить в группу первое и третье слагаемое и получить следующее выражение:
Метод группировки необходим для рационального вычисления значений выражений. Кроме того, он широко используется для упрощения и многих других задач разной степени сложности.
1 3 + 2 7 + 2 3 + 3 7 = 1 3 + 2 3 + 2 7 + 3 7 = 1 + 5 7 = 1 5 7
Один из способов разложения многочлена на отдельные множители также основан на группировке слагаемых.
Что такое группировка множителей
Такая группировка проводится точно таким же образом, как и при сложении, единственная разница в том, что работать предстоит не с суммами, а с произведениями. Она основана на переместительном и сочетательном свойствах умножения.
Группировка множителей – это объединение в одну группу нескольких множителей.
Процесс вычисления в данном случае проводится так же: сначала мы переставляем нужные множители так, чтобы они оказались рядом, а потом расставляем скобки.