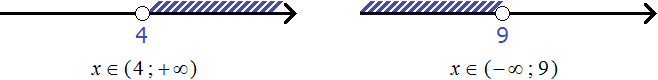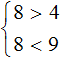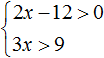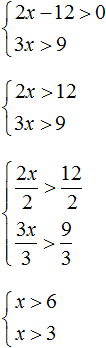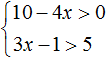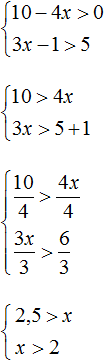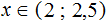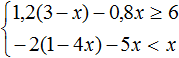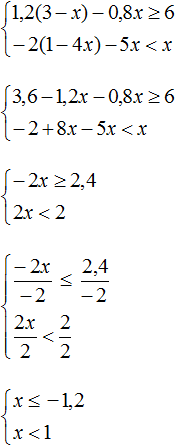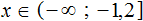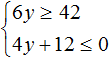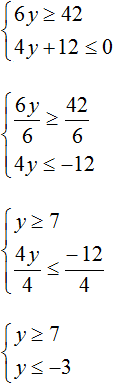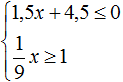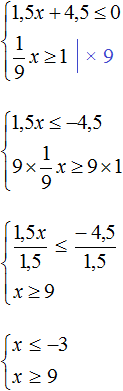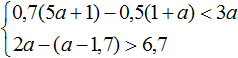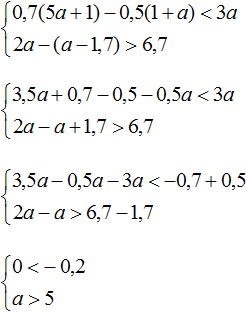Как решать систему неравенства
Системы линейных неравенств с одной переменной
Примеры решения систем линейных неравенств с одной переменной
Несколько линейных неравенств, удовлетворяющих одним и тем же решениям, образуют систему.
Рассмотрим простейший пример. Система 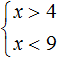
Решениями первого неравенства являются все числа, которые больше 4. Решениями второго неравенства являются все числа, которые меньше 9.
Изобразим множество решений каждого неравенства на координатной прямой и запишем ответы к ним в виде числовых промежутков:
Но дело в том, что неравенства x > 4 и x соединены знаком системы, а значит зависимы друг от друга. Им не дозволяется раскидываться решениями, как захочется. Наша задача указать решения, которые одновременно будут удовлетворять и первому неравенству и второму.
Говоря по-простому, нужно указать числа, которые больше 4, но меньше 9. Очевидно, что речь идет о числах, находящихся в промежутке от 4 до 9.
Значит решениями системы 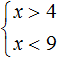
Также, нужно изобразить множество решений системы на координатной прямой.
Для системы линейных неравенств решение на координатной прямой изображают так:
Сначала указывают границы обоих неравенств:
На верхней области отмечают множество решений первого неравенства x > 4
Видим, что решение 8 удовлетворяет обоим неравенствам.
Исходя из рассмотренного примера, можно сформировать правило для решения системы линейных неравенств:
Чтобы решить систему линейных неравенств, нужно по отдельности решить каждое неравенство, и указать в виде числового промежутка множество решений, удовлетворяющих каждому неравенству.
Пример 2. Решить систему неравенств
Решениями первого неравенства являются все числа, которые больше 17. Решениями второго неравенства являются все числа, которые больше 12.
Решениями же обоих неравенств являются все числа, которые больше 17.
Изобразим множество решений системы 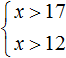
Для начала отметим на координатной прямой границы обоих неравенств:
На верхней области отметим множество решений первого неравенства x > 17
На нижней области отметим множество решений второго неравенства x > 12
Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы 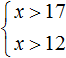
Пример 3. Решить систему неравенств
Решим каждое неравенство по отдельности. Делать это можно внутри системы. Если испытываете затруднения при решении каждого неравенства, обязательно изучите предыдущий урок
Получили систему 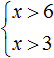
Как и в прошлом примере, сначала нужно отметить границы обоих неравенств, затем отметить множество решений каждого неравенства ( x > 6 и x > 3 ). Область координатной прямой, отмеченная с обеих сторон, будет промежутком, в котором располагается множество решений системы
Пример 4. Решить систему неравенств
Решим каждое неравенство по отдельности:
Изобразим множество решений системы 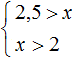
Пример 5. Решить неравенство
Решим каждое неравенство по отдельности:
Изобразим множество решений системы 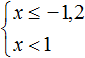
Когда решений нет
Если неравенства, входящие в систему, не имеют общих решений, то говорят, что система не имеет решений.
Пример 1. Решить неравенство
Решим каждое неравенство по отдельности:
Решениями первого неравенства являются все числа, которые больше 7, включая число 7. Решениями второго неравенства являются все числа, которые меньше −3, включая число −3.
Видим, что у данных неравенств нет общих решений. Увидеть это наглядно позволит координатная прямая. Отметим на ней множество решений каждого неравенства:
На координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Это говорит о том, что неравенства y ≥ 7 и y ≤ −3 не имеют общих решений. Значит не имеет решений система
А если не имеет решений приведённая равносильная система 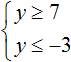
Ответ: решений нет.
Пример 2. Решить систему неравенств
Решим каждое неравенство по отдельности:
Изобразим множество решений неравенств x ≤ −3 и x ≥ 9 на координатной прямой:
Видим, что на координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Значит неравенства x ≤ −3 и x ≥ 9 не имеют общих решений. А значит не имеет решений система
А если не имеет решений приведённая равносильная система 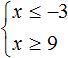
Ответ: решений нет.
Пример 3. Решить систему неравенств
Решим каждое неравенство по отдельности:
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение систем неравенств: линейные, квадратные и дробные.
Программа для решения линейных, квадратных и дробных неравенств не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Причём, если в процессе решения одного из неравенств нужно решить, например, квадратное уравнение, то его подробное решение также выводится (оно заключается в спойлер).
Данная программа может быть полезна учащимся старших классов при подготовке к контрольным работам, родителям для контроля решения неравенств их детьми.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
В качестве переменной может выступать любая латинсая буква.
Например: \( x, y, z, a, b, c, o, p, q \) и т.д.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе выражений можно использовать скобки. В этом случае при решении неравенства выражения сначала упрощаются.
Например: 5(a+1)^2+2&3/5+a > 0,6(a-2)(a+3)
Выберите нужный знак неравенства и введите многочлены в поля ниже.
Решение системы неравенств
В данной публикации мы рассмотрим, что такое система линейных неравенств, как она решается методом интервалов на числовой оси. Также разберем практические примеры по этой теме.
Определение системы неравенств
Для решения системы неравенств необходимо иметь навыки, позволяющие справиться с линейными неравенствами. Мы подробно рассмотрели этот вопрос в отдельной публикации.
Система неравенств – это два или более неравенства, объединенные фигурной скобкой. Например:
Т.е. она чем-то похожа на систему уравнений, в которых “равно” заменено на один из знаков сравнения (“больше”, “меньше”, “больше или равно”, “меньше или равно”).
Примечание: в системе линейных неравенств все они, соответственно, являются линейными. Обычно неизвестная переменная в них всего одна (чаще всего обозначается как “x” ).
Решение системы линейных неравенств
Алгоритм состоит из двух основных шагов:
Пример 1
Давайте попробуем решить систему, приведенную выше.
Теперь отметим на числовой оси полученные результаты, разделив области решений разными цветами для удобства восприятия.
Нам нужен участок, где присутствуют оба решения. Как мы видим на рисунке, он начинается с числа 10 включительно.
Пример 2
Найдем решение системы неравенств ниже:
Перенесем найденные решения на числовую ось и нарисуем соответствующие им интервалы:
Решение линейных неравенств
Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для сравнения величин.
| Символ | Название | Тип знака |
|---|---|---|
| > | больше | строгий знак (число на границе не включается ) |
| строгий знак (число на границе не включается ) | ||
| ≥ | больше или равно | нестрогий знак (число на границе включается ) |
| ≤ | меньше или равно | нестрогий знак (число на границе включается ) |
Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство отличается от уравнения.
В отличии от уравнения в неравенстве вместо знака равно « = » используют любой знак сравнения: « > », « », « ≤ » или « ≥ ».
Линейным неравенством называют неравенство, в котором неизвестное стоит только в первой степени.
Рассмотрим пример линейного неравенства.
Как решить линейное неравенство
Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное в первой степени с коэффициентом « 1 ».
При решении линейных неравенств используют правило переноса и правило деления неравенства на число.
Правило переноса в неравенствах
Также как и в уравнениях, в неравенствах можно переносить любой член неравенства из левой части в правую и наоборот.
Вернемся к нашему неравенству и используем правило переноса.
Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить, понятие числовой оси.
Нарисуем числовую ось для неизвестного « x » и отметим на ней число « 14 ».
При нанесении числа на числовую ось соблюдаются следующие правила:
Заштрихуем на числовой оси по полученному ответу « x » все решения неравенства, то есть область слева от числа « 14 ».
Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство « x − 6 » даст верный результат.
Возьмем, например число « 12 » из заштрихованной области и подставим его вместо « x » в исходное неравенство « x − 6 ».
Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства.
Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство дают верный результат.
Решением неравенства называют множество чисел из заштрихованной области на числовой оси.
В нашем примере ответ « x » можно понимать так: любое число из заштрихованной области (то есть любое число меньшее « 14 ») будет являться решением неравенства « x − 6 ».
Правило умножения или деления неравенства на число
Рассмотрим другое неравенство.
Используем правило переноса и перенесём все числа без неизвестного, в правую часть.
Теперь нам нужно сделать так, чтобы при неизвестном « x » стоял коэффициент « 1 ». Для этого достаточно разделить и левую, и правую часть на число « 2 ».
При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.
Разделим « 2x > 16 » на « 2 ». Так как « 2 » — положительное число, знак неравенства останется прежним.
Рассмотрим другое неравенство.
Разделим неравенство на « −3 ». Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.
Квадратные неравенства.
Метод интервалов
Прежде чем разбираться, как решать квадратное неравенство, давайте рассмотрим, какое неравенство называют квадратным.
Неравенство называют квадратным, если старшая (наибольшая) степень неизвестного « x » равна двум.
Потренируемся определять тип неравенства на примерах.
| Неравенство | Тип |
|---|---|
| x − 7 2 + 5x ≥ 0 | квадратное |
| 2x − 7 > 5 | линейное |
| x 2 + x − 12 ≤ 0 | квадратное |
Как решить квадратное неравенство
В предыдущих уроках мы разбирали, как решать линейные неравенства. Но в отличие от линейных неравенств квадратные решаются совсем иным образом.
Для решения квадратного неравенства используется специальный способ, который называется методом интервалов.
Что такое метод интервалов
Методом интервалов называют специальный способ решения квадратных неравенств. Ниже мы объясним, как использовать этот метод и почему он получил такое название.
Чтобы решить квадратное неравенство методом интервалов нужно:
Мы понимаем, что правила, описанные выше, трудно воспринимать только в теории, поэтому сразу рассмотрим пример решения квадратного неравенства по алгоритму выше.
Требуется решить квадратное неравенство.
Переходим к п.2. Необходимо сделать так, чтобы перед « x 2 » стоял положительный коэффициент. В неравенстве « x 2 + x − 12 » при « x 2 » стоит положительный коэффициент « 1 », значит, снова нам ничего делать не требуется.
Согласно п.3 приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение.
x1;2 =
| −1 ± √ 1 2 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
| −1 ± √ 1 + 48 |
| 2 |
x1;2 =
| −1 ± 7 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = −4 | x2 = 3 |
Теперь по п.4 отметим полученные корни на числовой оси в порядке возрастания.
Помните, что, исходя их того, какое перед нами неравенство (строгое или нестрогое) мы отмечаем точки на числовой оси разным образом.
Теперь, как сказано в п.5, нарисуем «арки» над интервалами между отмеченными точками.
Проставим знаки внутри интервалов. Справа налево чередуя, начиная с « + », отметим знаки.
Нам осталось только выполнить пункт 6, то есть выбрать нужные интервалы и записать их в ответ. Вернемся к нашему неравенству.
Запишем полученный ответ квадратного неравенства.
Именно из-за того, что при решении квадратного неравенства мы рассматриваем интервалы между числами, метод интервалов и получил свое название.
После получения ответа имеет смысл сделать его проверку, чтобы убедиться в правильности решения.
Выберем любое число, которое находится в заштрихованной области полученного ответа −4 и подставим его вместо « x » в исходное неравенство. Если мы получим верное неравенство, значит мы нашли ответ квадратного неравенства верно.
Возьмем, например, из интервала число « 0 ». Подставим его в исходное неравенство « x 2 + x − 12 ».
Мы получили верное неравенство при подстановке числа из области решений, значит ответ найден правильно.
Краткая запись решения методом интервалов
Сокращенно запись решения квадратного неравенства методом интервалов будет выглядеть так:
x 2 + x − 12 2 + x − 12 = 0
x1;2 =
| −1 ± √ 1 2 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
| −1 ± √ 1 + 48 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = −4 | x2 = 3 |

Другие примеры решения квадратных неравенств
Рассмотрим решение других примеров квадратных неравенств. Требуется решить квадратное неравенство:
В правой части неравенство уже стоит ноль. При « x 2 » стоит « 2 » ( положительный коэффициент), значит можно сразу переходить к поиску корней.
x1;2 =
| −(−1) ± √ (−1 2 ) − 4 · 2 · 0 |
| 2 · 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
x1 =
| x2 = 0 |

| 1 |
| 2 |
Рассмотрим пример, где перед « x 2 » в квадратном неравенстве стоит отрицательный коэффициент.
По п.2 общих правил решения методом интервалов нам нужно сделать так, чтобы перед « x 2 » стоял положительный коэффициент. Для этого умножим все неравенство на « −1 ».
Можно переходить к п.4 и п.5. Приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение. Затем расположим полученные корни на числовой оси и проведем между ними «арки».
x1;2 =
| −3 ± √ 3 2 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
| −3 ± √ 9 + 16 |
| 2 |
x2 =
| x1 =
| ||||
x2 =
| x1 =
| ||||
| x2 = −4 | x1 = 1 |

При определении того какие интервалы нам нужно брать в ответ, исходить нужно из самого последнего изменения неравенства перед нахождением его корней.
В нашем случае самая последняя версия неравенства перед поиском корней уравнения это « x 2 + 3x − 4 ≤ 0 ».
Значит для ответа нужно выбирать интервалы со знаком « − ».

К сожалению, при решении квадратного неравенства не всегда получаются два корня и все идет по общему плану выше. Возможны случаи, когда получается один корень или даже ни одного корня.
Как решить квадратные неравенства в таких случаях, мы разберем в следующем уроке «Квадратные неравенства с одним корнем или без корней».