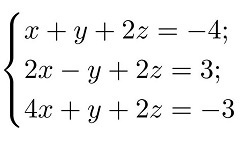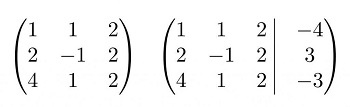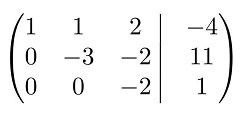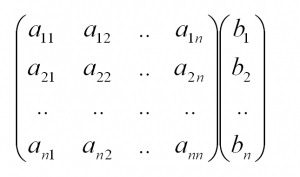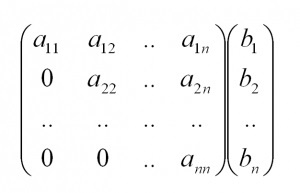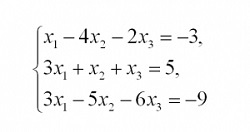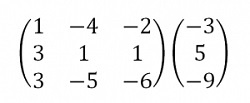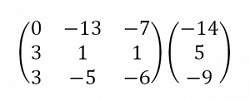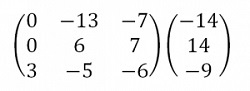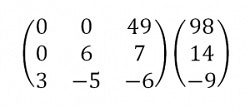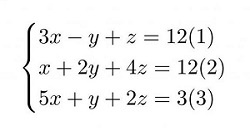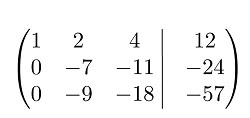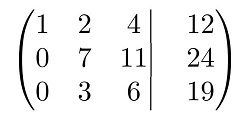Как решать системой гаусса

Метод Гаусса онлайн

Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.»

Предупреждение

Метод Гаусса

Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.

Эквивалентными преобразованиями системы линейных уравнений являются:

Рассмотрим систему линейных уравнений:

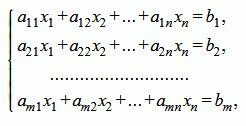(1)

Запишем систему (1) в матричном виде:

(3)

A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.

Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.

Построим расшренную матрицу системы:

(4)

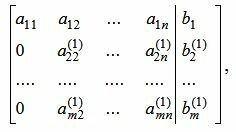(5)

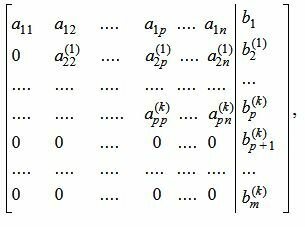(6)

Обратим внимание на последние строки. Если 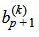. равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).

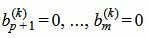
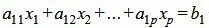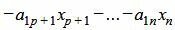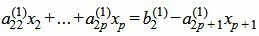Пусть . Тогда

(7)

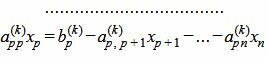Так как rangA=rang(A|b), то множество решений (7) есть (n−p)− многообразие. Следовательно n−p неизвестных можно выбрать произвольно. Остальные неизвестные из системы (7) вычисляются так. Из последнего уравнения выражаем x_p через остальные переменные и вставляем в предыдущие выражения. Далее из предпоследнего уравнения выражаем x_p−1 через остальные переменные и вставляем в предыдущие выражения и т.д. Рассмотрим метод Гаусса на конкретных примерах.

Примеры решения системы линейных уравнений методом Гаусса

Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, запишем расширенную матрицу:

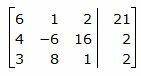Обозначим через a_ij элементы i-ой строки и j-ого столбца.

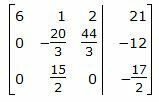Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 9/8:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Из вышеизложенной таблицы можно записать:

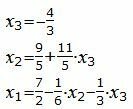Подставив верхние выражения в нижние, получим решение.

,,.

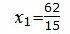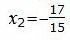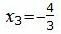Пример 2. Найти общее решение системы линейных уравнений методом Гаусса:

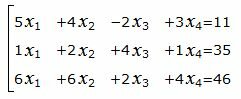Матричный вид записи: Ax=b, где

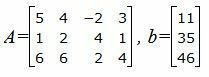Для решения системы, построим расширенную матрицу:

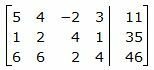Обозначим через a_ij элементы i-ой строки и j-ого столбца.

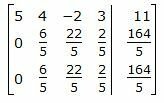Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Выразим переменные x₁, x₂ относительно остальных переменных.

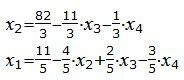где x₃, x₄− произвольные действительные числа.

Подставив верхние выражения в нижние, получим решение.

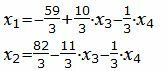где x₃, x₄− произвольные действительные числа.

Векторный вариант решения:

Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:

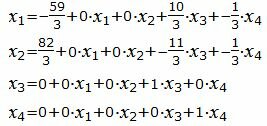Тогда векторное решение можно представить так:

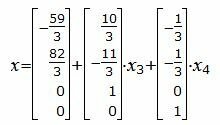где x₃, x₄− произвольные действительные числа.

Источник

Как решать уравнения методом Гаусса

Обновлено: 23 Августа 2021

Благодаря великим ученым было открыто множество эффективных теорем для работы со сложными математическими задачами. Один из таких примеров — метод Гаусса.

Метод Гаусса — что это такое

Метод Гаусса представляет собой методику эквивалентного преобразования исходной системы линейных уравнений в систему, решаемую существенно проще, чем исходный вариант.

Метод Гаусса используют для решения систем линейных алгебраических формул. Такой способ обладает рядом важных преимуществ:

Основные определения и обозначения

Матрицы: определение и свойства

Такие системы являются наиболее удобным способом представления данных, с которыми впоследствии производят манипуляции. Матрица имеет вид прямоугольника для удобства расчетов. При использовании метода Гаусса работа осуществляется с треугольными матрицами, при записи которых применяется прямоугольник с нулями на тех местах, где числа отсутствуют. Часто нули не записывают, а только подразумевают.

Важным параметром матрицы является размер:

Размер матрицы будет записан в формате А m*n. В случае, когда m=n, матрица является квадратной, а m=n служит ее порядком. Номера строк и столбцов изменяются.

Определитель

Матрица обладает крайне важной характеристикой. Таким параметром является определитель. Данную величину рассчитывают с помощью диагонали. Для этого в матрице необходимо провести воображаемые диагональные линии. Затем следует найти произведение элементов, которые располагаются на этих диагоналях, а полученные значения суммировать таким образом:

Рассчитать определитель представляется возможным лишь в случае работы с квадратной матрицей.

Если необходимо определить данный параметр для прямоугольной матрицы, то следует выполнить следующие манипуляции:

Элементы, которые расположены на пересечении отмеченных столбцов и строк, образуют новую квадратную матрицу. В случае, когда определитель является числом, не равным нулю, то данный параметр будет обозначен как базисный минор первоначальной прямоугольной матрицы. Перед решением систем уравнений методом Гаусса полезно рассчитать определитель. Если данная характеристика равна нулю, то матрица имеет бесконечное множество решений либо не имеет их вовсе. В таком случае потребуется определить ранг матрицы.

Классификация систем

Ранг матрицы является распространенным понятием. Он обозначает максимальный порядок ее определителя, который не равен нулю. По-другому можно сказать, что ранг матрицы представляет собой порядок базисного минора. Исходя из данного критерия, СЛАУ классифицируют на несколько типов. В совместных системах, которые состоят лишь из коэффициентов, ранг основной матрицы совпадает с рангом расширенной. Для подобных систем характерно одно или множество решений. По этой причине совместные системы подразделяют на следующие типы:

В несовместных системах ранги, характеризующие основную и расширенную матрицы, отличаются. С помощью метода Гаусса в процессе решения можно прийти либо к однозначному доказательству несовместности системы, либо к решению общего вида для системы, обладающей бесконечным количеством решений.

Основные правила и разрешаемые преобразования при использовании метода Гаусса

Перед тем, как решать систему, необходимо ее упростить. На данном этапе выполняют элементарные преобразования, которые не влияют на конечный результат. Определенные манипуляции справедливы лишь в случае матриц, исходниками которых являются СЛАУ. Список элементарных преобразований:

Особенности использования метода Гаусса для решения СЛАУ

На первом этапе система уравнений записывается в определенном виде. Пример выглядит следующим образом:

Коэффициенты необходимо представить в виде таблицы. С правой стороны в отдельном столбце записаны свободные члены. Данный блок отделен для удобства решения. Матрицу со столбцом со свободными членами называют расширенной.

Затем основная матрица с коэффициентами приводится к верхней треугольной форме. Данное действие является ключевым моментом при решении системы уравнений с помощью метода Гаусса. По итогам преобразований матрица должна приобрести такой вид, чтобы слева внизу находились одни нули:

При записи новой матрицы в виде системы уравнений можно отметить, что последняя строка уже содержит значение одного из корней, которое в дальнейшем подставляется в уравнение выше для нахождения следующего корня и так далее. Подобное описание позволяет разобраться в методе Гаусса в общих чертах.

Обратный и прямой ход метода Гаусса

В первом случае необходимо представить запись расширенной матрицы системы. При выполнении обратного метода Гаусса далее в главную матрицу добавляют столбец со свободными членами.

Суть такого способа заключается в выполнении элементарных преобразований, по итогам которых данная матрица приводится к ступенчатому или треугольному виду. В этом случае над или под главной диагональю матрицы располагаются только нули.

Варианты дальнейших действий:

Имея преобразованную систему с одной неизвестной Xn, которая становится известной, можно выполнить поиск в обратном порядке остальных неизвестных с помощью подстановки известных х в уравнения системы, вплоть до первого. Данный способ называют обратным методом Гаусса.

Примеры решений с объяснением

Пример 1

Требуется решить с помощью метода Гаусса систему линейных уравнений, которая выглядит следующим образом:

Необходимо записать расширенную матрицу:

Затем нужно выполнить преобразования. В результате матрица должна приобрести треугольный вид. Для этого следует умножить первую строку на (3) и умножить вторую строку на (-1). В результате суммирования второй и первой строк получается следующее:

Далее следует умножить третью строку на (-1). После добавления третьей строки ко второй получаем следующие преобразования:

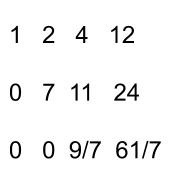
После этого необходимо умножить первую строку на (6) и вторую строку на (13). Далее следует добавить вторую строку к первой:

После того, как система преобразована, остается вычислить неизвестные:

Данный пример демонстрирует единственное решение системы.

Пример 2

Необходимо решить систему уравнений, которая выглядит следующим образом:

Необходимо составить матрицу:

Согласно методу Гаусса уравнение первой строки по итогам преобразований не меняется. Удобнее, когда левый верхний элемент матрицы обладает наименьшим значением. В таком случае первые элементы остальных строк после преобразований будут равны нулю. Таким образом, составленная матрица будет решаться проще, если на место первой строки поставить вторую:

Матрица с промежуточными результатами манипуляций будет иметь следующий вид:

Благодаря некоторым операциям можно придать матрице наиболее удобный вид. К примеру, вторую строку можно избавить от всех «минусов» путем умножения каждого элемента на «-1». Можно заметить, что для третьей строки характерны все элементы, кратные трем. В этом случае строка сокращается с помощью произведения каждого элемента на «-1/3». Минус позволит удалить отрицательные значения.

Далее следует приступить к манипуляциям со второй и третьей строками. Необходимо суммировать третью и вторую строки. Вторая строка при этом умножается на такой коэффициент, при котором элемент а 32 будет равен нулю.

В случае, когда некоторые преобразования приводят в результате к получению не целого числа, следует оставить его в этом виде. Таким образом, вычисления будут более точными. Затем при получении ответов можно определиться с его дальнейшем округлением или переводом в другую форму записи.

\(a»_ <32>= a_ <32>+ k×a_ <22>= 3 + (-3/7)×7 = 3 + (-3) = 0\)

Преобразованная матрица будет иметь следующий вид:

Матрица обладает ступенчатым видом. Дальнейшие преобразования с помощью метода Гаусса нецелесообразны. В этом случае можно удалить из третьей строки общий коэффициент «-1/7».

Затем необходимо представить запись матрицы в виде системы уравнений для вычисления корней.

Найти корни можно обратным методом Гаусса. Уравнение (3) содержит значение z:

С помощью первого уравнения можно определить х:

Подобная система является совместной и определенной, для которого характерно единственное решение. Ответ будет следующим:

Метод Гаусса предполагает последовательное исключение неизвестных. Методика справедлива в случае решения квадратных систем линейных алгебраических уравнений. Несмотря на простоту метода, многие студенты сталкиваются с некоторыми трудностями в процессе поиска правильного решения. Это связано с наличием знаков «+» и «-». Поэтому для решения СЛАУ требуется проявить внимательность. А получить квалифицированную помощь можно на ресурсе Феникс.Хелп.

Источник

Решение систем линейных уравнений методом Гаусса

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Понятие метода Гаусса

После того, как матрица системы приняла трапециевидную форму, уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.

У студентов наибольшие трудности вызывает именно прямой ход, то есть приведение исходной системы к трапециевидной. И это несмотря на то, что преобразования, которые необходимы для этого, называются элементарными. И называются неслучайно: в них требуется производить умножение (деление), сложение (вычитание) и перемену уравнений местами.

Преимущества метода:

Кроме того, метод Гаусса является основой одного из методов нахождения обратной матрицы.

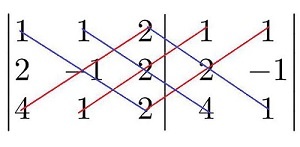
Чтобы все прониклись простотой, с которой решаются трапециевидные (треугольные, ступенчатые) системы линейных уравнений, приведём решение такой системы с применением обратного хода. Быстрое решение этой системы было показано на картинке в начале урока.

Пример 1. Решить систему линейных уравнений, применяя обратный ход:

Решение. В данной трапециевидной системе переменная z однозначно находится из третьего уравнения. Подставляем её значение во второе уравнение и получаем значение переменой y:

Из предыдущих шагов выписываем решение системы уравнений:

Чтобы получить такую трапециевидную систему линейных уравнений, которую мы решили очень просто, требуется применять прямой ход, связанный с элементарными преобразованиями системы линейных уравнений. Это также не очень сложно.

Элементарные преобразования системы линейных уравнений

На анимации выше показано, как система уравнений постепенно превращается в трапециевидную. То есть такую, которую вы видели на самой первой анимации и сами убедились в том, что из неё просто найти значения всех неизвестных. О том, как выполнить такое превращение и, конечно, примеры, пойдёт речь далее.

При решении систем линейных уравнений с любым числом уравнений и неизвестных в системе уравнений и в расширенной матрице системы можно:

В результате преобразований получаем систему линейных уравнений, эквивалентную данной.

Алгоритм и примеры решения методом Гаусса системы линейных уравнений с квадратной матрицей системы

Пример 2. Решить методом Гаусса систему линейных уравнений

Решая системы линейных уравнений школьными способами, мы почленно умножали одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами. При сложении уравнений происходит исключение этой переменной. Аналогично действует и метод Гаусса.

Для упрощения внешнего вида решения составим расширенную матрицу системы:

Для удобства деления коэффициентов при переменных (чтобы получить деление на единицу) переставим местами первую и вторую строки матрицы системы. Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения:

С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений. Для этого ко второй строке матрицы прибавим первую строку, умноженную на (в нашем случае на ), к третьей строке – первую строку, умноженную на (в нашем случае на ).

Это возможно, так как

Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям первую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.

В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменнную x:

Для упрощения второй строки полученной системы умножим её на и получим вновь матрицу системы уравнений, эквивалентной данной системе:

Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую строку, умноженную на (в нашем случае на ).

Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям вторую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.

В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений:

Мы получили эквивалентную данной трапециевидную систему линейных уравнений:

Если число уравнений и переменных больше, чем в нашем примере, то процесс последовательного исключения переменных продолжается до тех пор, пока матрица системы не станет трапециевидной, как в нашем демо-примере.

Из первого уравнения найдём x:

Проверить решение системы можно и на калькуляторе, решающем методом Крамера: в этом случае будет выдан тот же ответ, если система имеет однозначное решение. Если же система имеет бесконечное множество решений, то таков будет и ответ, и это уже предмет пятой части этого урока.

Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение

Пример 3. Решить систему линейных уравнений:

Пример 4. Решить систему линейных уравнений методом Гаусса:

Теперь с помощью третьего уравнения исключим переменную из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на . Получаем расширенную матрицу трапециевидной формы.

Получили систему уравнений, которой эквивалентна заданная система:

Следовательно, полученная и данная системы являются совместными и определёнными. Окончательное решение находим «с конца». Из четвёртого уравнения непосредственно можем выразить значение переменной «икс четвёртое»:

.

Это значение подставляем в третье уравнение системы и получаем

,

откуда находим «икс третье»:

.

Далее, подставляем значения и во второе уравнение системы:

,

.

Наконец, подстановка значений

в первое уравнение даёт

,

откуда находим «икс первое»:

.

Ответ: данная система уравнений имеет единственное решение .

Проверить решение системы можно и на калькуляторе, решающем методом Крамера: в этом случае будет выдан тот же ответ, если система имеет однозначное решение.

Решение методом Гаусса прикладных задач на примере задачи на сплавы

Решение. Составляем систему линейных уравнений:

Умножаем второе и третье уравнения на 10, получаем эквивалентную систему линейных уравнений:

Составляем расширенную матрицу системы:

Прямой ход завершился. Получили расширенную матрицу трапециевидной формы.

Применяем обратный ход. Находим решение с конца. Видим, что .

Из второго уравнения находим

,

.

Проверить решение системы можно и на калькуляторе, решающем методом Крамера: в этом случае будет выдан то же ответ, если система имеет однозначное решение.

С помощью метода Гаусса можно установить, совместна или несовместна любая система n линейных уравнений с n переменными.

Метод Гаусса и системы линейных уравнений, имеющие бесконечное множество решений

После выполнения преобразований в расширенной матрице системы (перестановки строк, умножения и деления строк на некоторое число, прибавлению к одной строке другой) могли появиться строки вида

,

соответствующие уравнению вида

Если во всех уравнениях имеющих вид

свободные члены равны нулю, то это означает, что система неопределённа, то есть имеет бесконечное множество решений, а уравнения этого вида – «лишние» и их исключаем из системы.

Пример 6. Решить методом Гаусса систему линейных уравнений:

Решение. Составим расширенную матрицу системы. Затем с помощью первого уравнения исключим переменную из последующих уравнений. Для этого ко второй, третьей и четвёртой строкам прибавим первую, умноженную соответственно на :

Теперь вторую строку прибавим к третьей и четвёртой.

В результате приходим к системе

Последние два уравнения превратились в уравнения вида . Эти уравнения удовлетворяются при любых значениях неизвестных и их можно отбросить.

Чтобы удовлетворить второму уравнению, мы можем для и выбрать произвольные значения , тогда значение для определится уже однозначно: . Из первого уравнения значение для также находится однозначно: .

Как заданная, так и последняя системы совместны, но неопределённы, и формулы

при произвольных и дают нам все решения заданной системы.

Метод Гаусса и системы линейных уравнений, не имеющие решений

Как уже говорилось в связи с первым примером, после выполнения преобразований в расширенной матрице системы могли появиться строки вида

,

соответствующие уравнению вида

Если среди них есть хотя бы одно уравнение с отличным от нуля свободным членом (т.е. ), то данная система уравнений является несовместной, то есть не имеет решений и на этом её решение закончено.

Пример 7. Решить методом Гаусса систему линейных уравнений:

Теперь нужно с помощью второго уравнения исключить переменную из последующих уравнений. Чтобы получить целые отношения коэффициентов, поменяем местами вторую и третью строки расширенной матрицы системы.

Теперь с помощью третьего уравнения исключим переменную из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на .

Заданная система эквивалентна, таким образом, следующей:

Полученная система несовместна, так как её последнее уравнение не может быть удовлетворено никакими значениями неизвестных. Следовательно, данная система не имеет решений.

Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение

Пример 8. Решить систему линейных уравнений:

Метод Гаусса и системы, в которых число неизвестных меньше числа уравнений

Пример 9. Решить методом Гаусса систему линейных уравнений:

Теперь нужно с помощью второго уравнения исключить переменную из последующих уравнений. Проведём подготовительные работы. Чтобы было удобнее с отношением коэффициентов, нужно получить единицу в во втором столбце второй строки. Для этого четвёртую строку умножаем на , а полученную в результате четвёртую строку меняем местами со второй строкой.

Получили следующую систему уравнений, которой эквивалентна заданная система:

и известны, а находим из первого уравнения:

.

Ответ: данная система уравнений имеет единственное решение (1; 1; 1).

Метод Гаусса и системы, в которых число неизвестных больше числа уравнений

Если при выполнении преобразований в расширенной матрице системы встретилось хотя бы одно уравнение вида

(*)

с равным нулю свободным членом, то в итоге получим эквивалентную исходной системе систему линейных уравнений, в которой число уравнений меньше числа переменных, а уравнения вида (*) удовлетворяются при любых значениях неизвестных. Их можно отбросить.

Неизвестным, которые удовлетворяли уравнению вида 0 = 0, например, третьему и четвёртому (*, отброшенным уравнениям), придадим произвольные значения (пример 2). Они чаще всего записываются так: . Подставляя эти значения в остальные уравнения, не имеющие вида (*), например, первое и второе, получаем формулы, дающие нам значения остальных неизвестных. В них можно подставлять любые численные значения и . Следовательно, существует бесконечное множество выбора значений этих неизвестных, поэтому полученная система уравнений является неопределённой. В этом случае неопределённой является и исходная система.

Пример 10. Решить методом Гаусса систему линейных уравнений:

Решение. Составляем расширенную матрицу системы. Далее ко второй строке прибавляем первую, умноженную на .

Заданная система эквивалентна, таким образом, следующей:

В ней отсутствуют уравнения, дающие однозначные значения для и . Это равносильно появлению уравнений вида , которые можно отбросить. Мы можем для и выбрать произвольные значения . Из первого уравнения значение для находится однозначно: .

Как заданная, так и последняя системы совместны, но неопределённы, и формулы

при произвольных и дают нам все решения заданной системы.

Источник