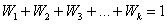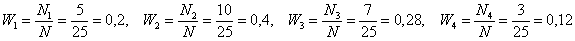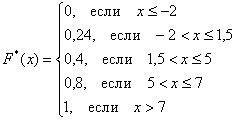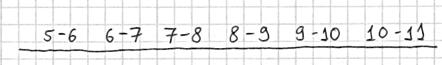Как решать ряд распределения
2. Дискретный вариационный ряд.
Полигон частот и эмпирическая функция распределения
На вводном уроке по математической статистике мы узнали, что такое математическая статистика, и теперь обо всём подробнее. Далее для удобства я буду нумеровать статьи и постараюсь делать их не слишком длинными. Потому что всё действительно просто, и главное, здесь научиться рациональной технике вычислений, на которую и будет сделан особый упор.
Интервальные и дискретные вариационные ряды почти сразу же встретились в предыдущей статье, и мы начинаем с дискретного случая, когда количественная эмпирическая величина 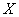
…что-то не понятно по терминам? Срочно изучать первый урок! (ссылка выше)
Дискретный вариационный ряд – это упорядоченное по возрастанию (как правило) множество вариант 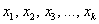
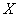
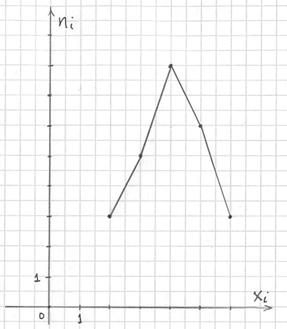
Частоты выборочной совокупности обозначают через 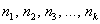
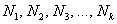
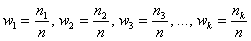
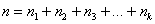
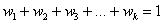
Аналогично для совокупности генеральной: 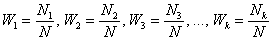
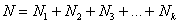
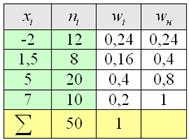
И тут вспоминается Пример 2 об оценках по матанализу в группе из 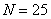
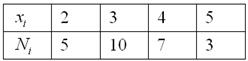
– пожалуйста, пример дискретного вариационного ряда, где варианты 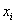
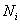
Для разминки найдём относительные частоты:
и непременно проконтролируем, что: 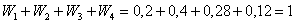
Все вычисления обычно проводят на калькуляторе либо в Экселе, а результаты заносят в таблицу, при этом, в статистике данные чаще располагают не в строках, а в столбцах: 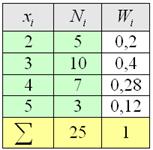
Такое расположение обусловлено тем, что количество вариант может быть достаточно велико, и они просто не вместятся в строчку. Не редкость, когда их 10-20, а бывает, и 100-200, что тоже и неоднократно встречалось в моей практике. И это не какие-то супер-пупер расчёты, а учебные задачи!
После сей позитивной новости продолжаем 🙂
Откуда берутся дискретные вариационные ряды? Такие ряды появляются в результате учёта дискретной характеристики статистической совокупности, причём, варианты ряда не отличаются большим разнообразием. Например, оценки (коих не так много) в примере выше.
И сейчас мы примем непосредственное участие в этом процессе:
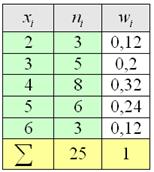
По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3. Требуется:
– составить вариационный ряд и построить полигон частот;
– найти относительные частоты и построить эмпирическую функцию распределения.
Чего томиться? – вся тема урока в одной задаче!
Решение: в условии прямо сказано о том, что перед нами выборка из генеральной совокупности (всех рабочих цеха), и первое, что логично сделать – подсчитать её объем, т.е. количество рабочих. В данном случае это легко сделать устно: 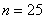
Квалификационные разряды – есть величина дискретная, и поэтому нам предстоит составить дискретный вариационный ряд (обратите внимание, что в условии ничего не сказано о характере ряда).
Если у вас под рукой нет вычислительных программ, то вручную (Эксель разберём ниже). При этом оптимальным может быть следующий алгоритм: сначала окидываем взглядом все числа и определяем среди них минимальное (примерно) и максимальное (примерно). В данном случае ориентировочный диапазон – от 1 до 7. Записываем их в столбец на черновике и обводим в кружочки. Далее начинаем вычёркивать карандашом числа из исходного списка: 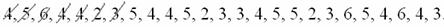
и делать около соответствующих кружков засечки:
После того, как все числа будут вычеркнуты, подсчитываем количество засечек в каждой строке: 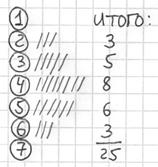
И обязательно проверяем, получается ли у нас в сумме объём выборки 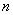
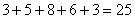

…ну что же, вполне и вполне логично – рабочих средней квалификации много, а учеников и мастеров – мало. Полученные результаты позволяют достаточно точно судить об уровне квалификации всего цеха (если, конечно, выборка представительна)
Построенный вариационный ряд также называют статистическим распределением выборки, причём, этот термин применИм не только для дискретного, но и для интервального ряда, который мы рассмотрим на следующем уроке.
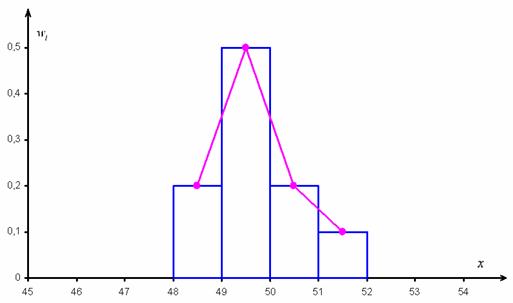
Построим полигон частот. Это статистический аналог многоугольника распределения дискретной случайной величины (кто изучал). Полигон частот – это ломаная, соединяющая соседние точки 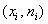
…эх, ностальгия. Но, пятилетку-другую, думается, так решать ещё будут.
Теперь современный способ:
Решаем! – исходные данные с пошаговой инструкцией прилагаются.
Вторая часть задачи. Найдём относительные частоты 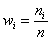
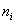

– обязательно проверяем, что сумма относительных частот равна единице!
Иногда требуется построить полигон относительных частот. Как вы правильно догадываетесь – это ломаная, соединяющая соседние точки 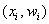
А теперь посмотрим на относительные частоты и задумаемся, на что они похожи? …Правильно, на вероятности. Так, например, можно сказать, что 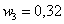
А вот если учесть ВСЕХ рабочих цеха (всю генеральную совокупность), то рассчитанные относительные частоты 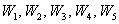
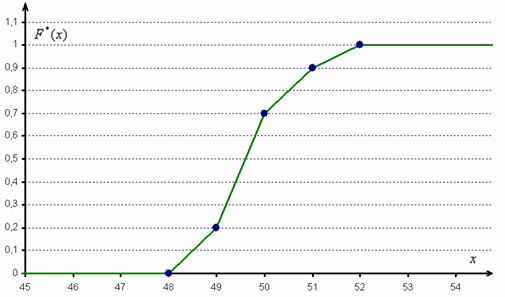
Построим эмпирическую функцию распределения 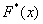
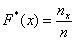
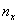
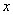
при этом «икс» «пробегает» все значения от «минус» до «плюс» бесконечности.
Очевидно, что на интервале 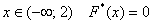
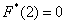
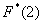
На промежутке 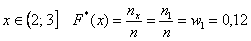
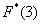
На промежутке 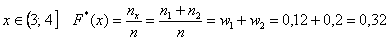
– если 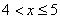

– если 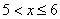
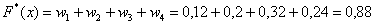
– и, наконец, если 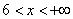
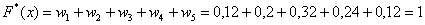
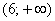
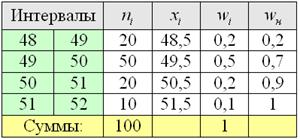
Накопленные относительные частоты удобно записывать в отдельный столбец таблицы, при этом алгоритм вычислений очень прост: сначала сносим слева 1-е значение (красная стрелка), а каждое следующее получаем как сумму предыдущего и относительной частоты из текущего левого столбца (зелёные обозначения): 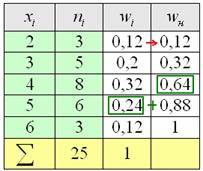
Вот, кстати, ещё один довод за вертикальную ориентацию данных – справа по надобности можно приписывать дополнительные столбцы.
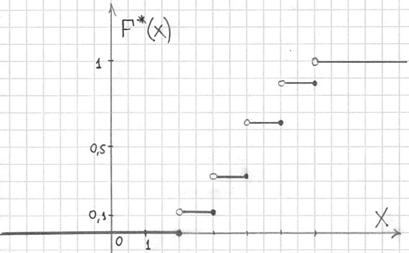
Саму функцию принято записывать в кусочном виде:
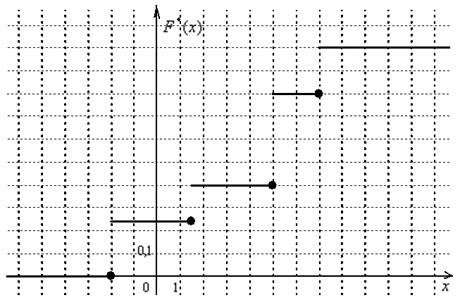
а её график представляет собой ступенчатую фигуру:
Эмпирическая функция распределения не убывает и принимает значения из промежутка 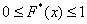
И сейчас мы автоматизируем процесс; видео, к сожалению, не вписалось по ширине, посему смотрим его на Ютубе:

Эмпирическая функция распределения 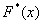
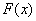
Миниатюрная задача для закрепления материала:
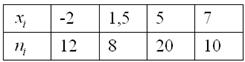
Дано статистическое распределение выборки
Составить эмпирическую функцию распределения, выполнить чертёж
Самостоятельно решить Пример 5 в Экселе, все числа и обозначения уже там.
Свериться с образцом можно ниже. По поводу красоты чертежа сильно не запаривайтесь, главное, чтобы было правильно – этого обычно достаточно для зачёта.
И я жду вас на третьем уроке, где речь пойдёт об интервальном вариационном ряде.
Пример 5. Решение: заполним расчётную таблицу:
Составим эмпирическую функцию распределения:
Выполним чертёж:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

3. Интервальный вариационный ряд.
Гистограмма относительных частот
На предыдущем уроке по математической статистике (Занятие 1) мы разобрали дискретный вариационный ряд (Занятие 2), и сейчас на очереди интервальный. Его понятие, графическое представление (гистограмма и эмпирическая функция распределения), а также рациональные методы вычислений, как ручные, так и программные. В том числе будут рассмотрены задачи с достаточно большим количеством (100-200) вариант – что делать в таких случаях, как обработать большой массив данных.
Предпосылкой построения интервального вариационного ряда (ИВР) является тот факт, что исследуемая величина принимает слишком много различных значений. Зачастую ИВР появляется в результате измерения непрерывной характеристики изучаемых объектов. Типично – это время, масса, размеры и другие физические характеристики. Подходящие примеры встретились в первой же статье по матстату, вспоминаем Константина, который замерял время на лабораторной работе и Фёдора, который взвешивал помидоры.
Для изучения интервального вариационного ряда затруднительно либо невозможно применить тот же подход, что и для дискретного ряда. Это связано с тем, что ВСЕ варианты многих ИВР различны. И даже если встречаются совпадающие значения, например, 50 грамм и 50 грамм, то связано это с округлением, ибо полученные значения всё равно отличаются хоть какими-то микрограммами.
Поэтому для исследования ИВР используется другой подход, а именно, определяется интервал, в пределах которого варьируются значения, затем данный интервал делится на частичные интервалы, и по каждому интервалу подсчитываются частоты – количество вариант, которые в него попали.
Разберём всю кухню на конкретной задаче, и чтобы как-то разнообразить физику, я приведу пример с экономическим содержанием, кои десятками предлагают студентам экономических отделений. Деньги, строго говоря, дискретны, но если надо, непрерывны :), и по причине слишком большого разброса цен, для них целесообразно строить интервальный ряд:
По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные (в некоторых денежных единицах): 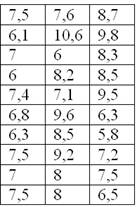
Требуется составить вариационный ряд распределения, построить гистограмму и полигон относительных частот + бонус – эмпирическую функцию распределения.
Такое обывательское исследование проводит каждый из нас, начиная с анализа цены на пакет молока вот это дожил в нескольких магазинах, и заканчивая ценами на недвижимость по гораздо бОльшей выборке. Что называется, не какие-то там унылые сантиметры.
Поэтому представьте свой любимый товар / услугу и наслаждайтесь решением🙂
Очевидно, что перед нами выборочная совокупность объемом 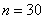
Начнём с экстремальной ситуации, когда у вас под рукой нет Экселя или другого подходящего программного обеспечения. Только ручка, карандаш, тетрадь и калькулятор.
Тактика действий похожа на исследование дискретного вариационного ряда. Сначала окидываем взглядом предложенные числа и определяем примерный интервал, в который вписываются эти значения. «Навскидку» все значения заключены в пределах от 5 до 11. Далее делим этот интервал на удобные подынтервалы, в данном случае напрашиваются промежутки единичной длины. Записываем их на черновик:
Теперь начинаем вычёркивать числа из исходного списка и записывать их в соответствующие колонки нашей импровизированной таблицы: 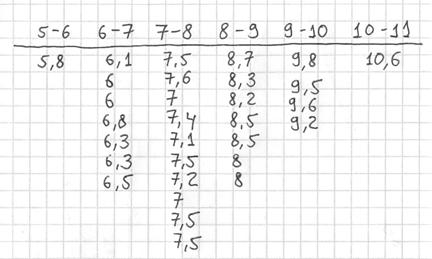
После этого находим самое маленькое число в левой колонке и самое большое значение – в правой. Тут даже ничего искать не пришлось, честное слово, не нарочно получилось:)
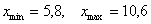
Вычислим размах вариации:
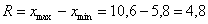
Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на этот счёт существует формула Стерджеса:
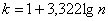
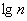
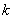
* есть на любом более или менее приличном калькуляторе
В нашем случае получаем:
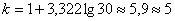
Следует отметить, что правило Стерджеса носит рекомендательный, но не обязательный характер. Нередко в условии задачи прямо сказано, на какое количество интервалов нужно проводить разбиение (на 4, 5, 6, 10 и т.д.), и тогда следует придерживаться именно этого указания.
Длины частичных интервалов могут быть различны, но в большинстве случаев использует равноинтервальную группировку:
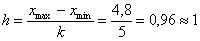
И коль скоро мы прибавили 0,04, то по 5 частичным интервалам у нас получается «перебор»: 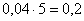
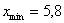
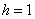
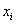
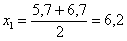
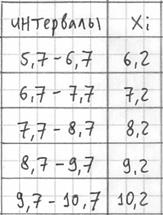
– убеждаемся в том, что самая большая варианта 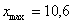
Далее подсчитываем частоты по каждому интервалу. Для этого в черновой «таблице» обводим значения, попавшие в тот или иной интервал, подсчитываем их количество и вычёркиваем: 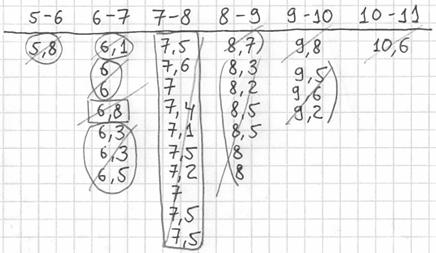
Так, значения из 1-го интервала я обвёл овалами (7 штук) и вычеркнул, значения из 2-го интервала – прямоугольниками (11 штук) и вычеркнул и так далее.
Правило: если варианта попадает на «стык» интервалов, то её следует относить в правый интервал. У нас такая варианта встретилась одна: 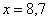
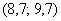
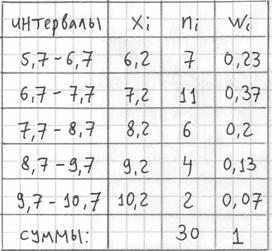
В результате получаем интервальный вариационный ряд, при этом обязательно убеждаемся в том, что ничего не потеряно: 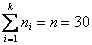
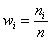
Дело за чертежами. Для ИВР чаще всего требуется построить гистограмму.
Гистограмма относительных частот – это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов, а высота – соответствующим относительным частотам: 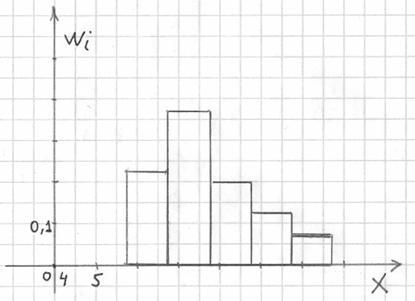
При этом вполне допустимо использовать нестандартную шкалу по оси абсцисс, в данном случае я начал нумерацию с четырёх.
Площадь гистограммы равна единице, и это статистический аналог функции плотности распределения непрерывной случайной величины. Построенный чертёж даёт наглядное и весьма точное представление о распределении цен на ботинки по всей генеральной совокупности. Но это при условии, что выборка представительна.
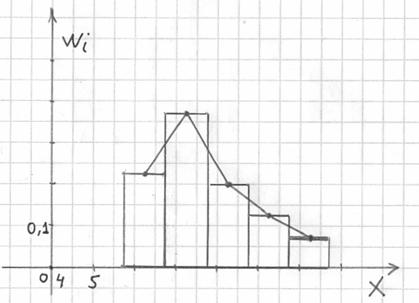
Вместе с гистограммой нередко требуют построить полигон. Без проблем, полигон относительных частот – это ломаная, соединяющая соседние точки 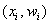
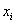
Автоматизируем решение в Экселе:

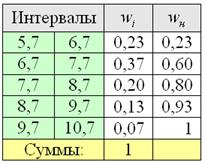
И бонус – эмпирическая функция распределения. Она определяется точно так же, как в дискретном случае:
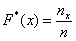
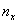
Но вот построить её для интервального ряда намного проще. Находим накопленные относительные частоты:
И строим кусочно-ломаную линию, с промежуточными точками 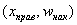
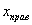
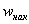
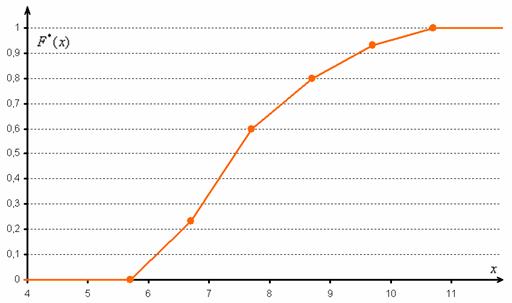
При этом 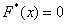
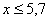
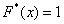
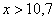
Напоминаю, что данная функция не убывает, принимает значения из промежутка 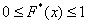
Эмпирическая функция распределения является аналогом функции распределения НСВ и приближает теоретическую функцию 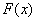
Помимо перечисленных графиков, вариационные ряды также можно представить с помощью кумуляты и огивы частот либо относительных частот, но в классическом учебном курсе эта дичь редкая, и поэтому о ней буквально пару абзацев:
Кумулята – это ломаная, соединяющая точки:
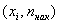
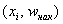
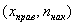
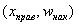
* 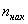
В последнем случае кумулята относительных частот 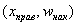
Огива – это обратная функция по отношению к кумуляте – здесь варианты откладываются по оси ординат, а накопленные частоты либо относительные частоты – по оси абсцисс.
С построением данных линий, думаю, проблем быть не должно, чего не скажешь о другой проблеме. Хорошо, если в вашей задаче всего лишь 20-30-50 вариант, но что делать, если их 100-200 и больше? В моей практике встречались десятки таких задач, и ручной подсчёт здесь уже не торт. Считаю нужным снять небольшое видео:

Ну, теперь вы монстры 8-го уровня 🙂
Но не всё так сурово. В большинстве задач вам предложат готовый вариационный ряд, и на счёт молока, то, конечно, была шутка:
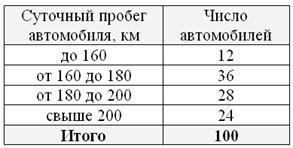
Выборочная проверка партии чая, поступившего в торговую сеть, дала следующие результаты:
Требуется построить гистограмму и полигон относительных частот, эмпирическую функцию распределения
Проверяем свои навыки работы в Экселе! (исходные числа и краткая инструкция прилагается) И на всякий случай краткое решение для сверки в конце урока.
Что ещё важного по теме? Время от времени встречаются ИВР с открытыми крайними интервалами, например:
В таких случаях, что убийственно логично, интервалы «закрывают». Обычно поступают так: сначала смотрим на средние интервалы и выясняем длину частичного интервала: 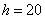
Ну вот, пожалуй, и вся практически важная информация по ИВР.
На очереди числовые характеристики вариационных рядов и начнём мы с их центральных характеристик, а именно – Моды, медианы и средней.
Пример 7. Решение: заполним расчётную таблицу
Построим гистограмму и полигон относительных частот:
Построим эмпирическую функцию распределения:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5