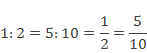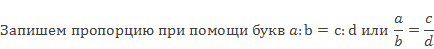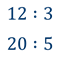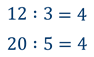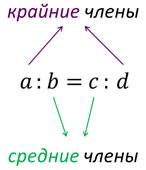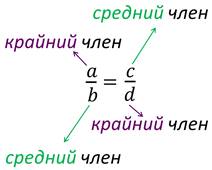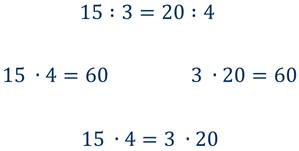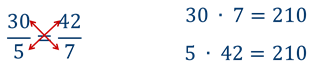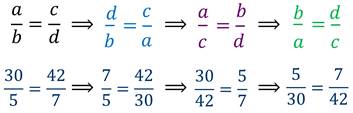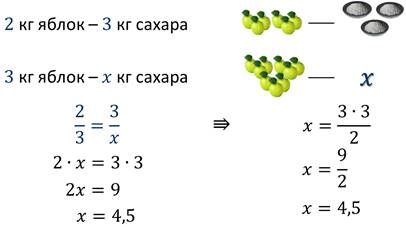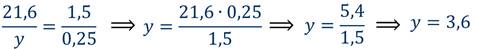Как решать пропорции видеоурок
Как решать пропорции видеоурок
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке Вы узнаете, что такое пропорция, познакомитесь с основным ее свойством. А также научитесь составлять пропорции и находить неизвестный член пропорции.
Давайте вспомним, что такое отношение двух чисел.
Частное двух чисел называют отношением этих чисел.
Читают так: отношение пяти к семи или отношение чисел пять и семь.
Рассмотрим отношение 1 : 2 и отношение 5 : 10. Как частные они имеют значения. Значение первого отношения – 0,5 и второго – 0,5.
Значит, они равны, и можно записать:
Равенство двух отношений называют пропорцией.
Читается так: «Отношение а к b равно отношению с к d» или «а так относится к b, как с относится к d».
В пропорции числа а и d называют крайними членами пропорции, а b и с называют средними членами пропорции.
Давайте в нашей пропорции 1 : 2=5 : 10 найдем произведение её крайних и средних членов.
Получим 1 ∙ 10=10; 2 ∙ 5=10. Значит, 1 ∙ 10=2∙5
Таким образом, можно сделать вывод:
В верной пропорции произведение крайних членов пропорции равно произведению её средних членов. А в буквенном выражении: а, умноженное на d, равно в, умноженное на с.
Верно и обратное утверждение:
Если произведение крайних членов пропорции равно произведению средних членов пропорции, то пропорция верна.
Именно это свойство называют основным свойством пропорции.
Это утверждение можно использовать при доказательствах.
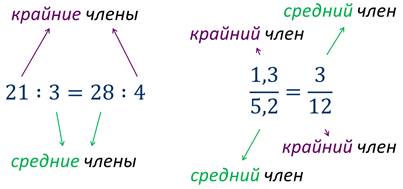
Например, пропорция 15 : 3=25 : 5 верна, так как 15 ∙ 5=3 ∙ 25=75.
Используя основное свойство пропорции, можно найти неизвестный член пропорции, но при условии, что все остальные её члены известны.
Например: найдем неизвестный средний член пропорции 7 : а = 3 : 6, воспользуемся основным свойством пропорции, 7 ∙ 6 = а ∙ 3, а = 7 ∙ 6 : 3 = 14, т.е. неизвестный член пропорции а равен 14.
Отметим, что если в верной пропорции поменять местами средние члены пропорции или крайние члены пропорции, то новые пропорции, которые у нас получатся, будут тоже верными.
Например: 24 : 12 = 8 : 4
Воспользуемся основным свойством пропорции, получим 24 ∙ 4 = 12 ∙ 8 = 96.
Поменяем в пропорции средние члены, получим 24 : 8 = 12 : 4, воспользуемся основным свойством пропорции, получим 24 ∙ 4 = 8 ∙ 12 = 96.
Теперь поменяем местами крайние члены пропорции, получим 4 : 12 = 8 : 24, воспользуемся основным свойством пропорции, получаем 4 ∙ 24 = 12 ∙ 8 = 96.
Видим, что получившиеся пропорции тоже верны, так как при таких перестановках произведение крайних и средних членов пропорции не изменилось.
Итак, на этом уроке Вы узнали, что такое пропорция, познакомились с основным её свойством. А также научились составлять пропорции и находить неизвестный член пропорции.
Как решать пропорции видеоурок
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке разберем, что такое прямая и обратная пропорциональные зависимости, а также решим задачи на пропорциональные величины.
Две величины называют прямо пропорциональными, если при увеличении или уменьшении одной из них в несколько раз другая величина соответственно увеличивается или уменьшается во столько же раз.
Рассмотрим прямую пропорциональную зависимости на примере следующей задачи.
За два часа спортсмен пробежал 20 километров, сколько километров он пробежит за 6 часов, если его скорость не изменится?
Время спортсмена в пути увеличится в три раза, значит и количество километров, которое спортсмен пробежит, тоже увеличится в три раза, так как спортсмен бежит с постоянной скоростью. Во сколько раз увеличится время, во столько же раз увеличится расстояние. Зависимость между временем и расстоянием в данном случае прямо пропорциональна.
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны. Значит, отношения значений времени 2 : 6 и значений расстояния 20 : х равны, следовательно, верна пропорция 2 : 6 = 20 : х. Теперь найдем неизвестный член пропорции: х = 6 · 20 : 2 = 60. Получаем, 60 километров пробежит спортсмен за 6 часов.
Две величины называют обратно пропорциональными, если пр. и увеличении или уменьшении одной из них в несколько раз другая величина соответственно уменьшается или увеличивается во столько же раз.
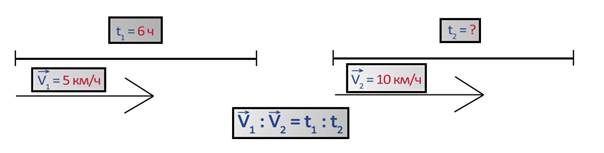
Рассмотрим и обратную пропорциональную зависимость на примере. Задача: Спортсмен пробежал расстояние со скоростью 5 км/ч за 6 часов, за сколько часов спортсмен пробежит это расстояние, если скорость его увеличится вдвое?
Если скорость увеличится вдвое, она будет равна 10 км/ч, и данное расстояние спортсмен пробежит быстрее вдвое, то есть затратит вдвое меньше времени на прохождение этого расстояния. Во сколько раз увеличится скорость, во столько раз уменьшится время его движения. Зависимость между скоростью движения и временем в пути в данном случае обратно пропорциональна.
Если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины. Значит, отношение значений скорости 5 : 10 будет равно не отношению 6 : х, а обратному отношению соответствующих значений времених:6. Значит, верна пропорция 5 : 10 = х : 6, решаем:
х = 5 · 6 : 10 = 3. Получаем, что это же расстояние спортсмен пробежит за 3 часа, если его скорость увеличится вдвое.
Отметим, что не всякие две величины являются прямо пропорциональными или обратно пропорциональными. Например, зависимость между возрастом человека и размером его обуви. При удвоении возраста человека размер его обуви не удваивается, поэтому величины возраст и размер обуви не являются пропорциональными. Не будут пропорциональными время и расстояние в нашей первой задаче, если скорость спортсмена не будет постоянной.
Пропорции
Урок 21. Математика 6 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Пропорции»
На этом уроке мы узнаем, что такое пропорция. Познакомимся с основным свойством пропорции. Научимся решать пропорции. А также ответим на вопрос, является ли данная пропорция верной.
Очень часто в жизни мы сталкиваемся со словом «пропорция». Наверняка вы слышали о пропорциях в человеческом теле!
Вообще пропорция – это широко распространённый термин, который используется во многих областях человеческой деятельности. Можно услышать о пропорциях в кулинарии, медицине, архитектуре.
Также пропорции тесно связаны с наукой. Без пропорций не могут химики, биологи, географы, физики и т.д..
Само слово пропорция происходит от латинского слова proportio, что переводится как соотношение, соразмерность.
Давайте разберёмся, что же вкладывают математики в слово пропорция.
Рассмотрим два отношения. Мы знаем с прошлых уроков, что отношение – это частное двух неравных нулю чисел (или величин).
Нетрудно посчитать, чему же равны значения этих частных:
Видно, что и в первом и во втором случае значения частных равны. А значит и сами отношения равны.
Давайте прочитаем равенство, которое получилось: «12 так относится к трём, как 20 к пяти».
Такое равенство в математике называют пропорцией.
На прошлых уроках мы уточнили, что отношение можно записывать как при помощи знака деления, так и при помощи черты дроби. Следовательно, пропорцию можно записать ещё в виде равенства обыкновенных дробей:
Пропорция – это равенство двух отношений.
Раз пропорцию можно записать в виде частного двух натуральных чисел, обыкновенными дробями, то пропорцию можно записать и в буквенном виде.
Пропорцию можно прочитать так: «a так относится к b, как c относится к d», или так «отношение a к b равно отношению c к d», или ещё так «a, деленное на b равно c, делённому на d».
Договариваются, что все члены пропорции отличны от нуля.
Что очень хорошо видно из равенства на экране.
Смотрите a и d расположены по краям пропорции, b и c – посередине. Эти названия сохраняются и тогда, когда пропорция записана в виде:
Как вы думаете можно ли как-нибудь убедиться в том, что пропорция составлена верно? Конечно, да!
В любой верной пропорции произведение крайних членов равно произведению средних членов пропорции, т.е.
Это утверждение называется основным свойством пропорции.
Верно и обратное утверждение: если произведение крайних членов равно произведению средних членов a · d = b · c, то пропорция a : b = c : d верна. Оно называется признаком пропорции.
Но ведь пропорцию записывают и в виде: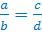 
. Чтобы не перепутать, какие члены пропорции нужно перемножить, посмотрите, как они расположены в пропорции:
Они лежат «крест-накрест»!
Например, есть пропорция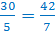 
. Проверим верна ли она.
Следовательно, пропорция верна!
Если в верной пропорции поменять местами средние члены и крайние члены, то получившиеся новые пропорции также верны.
Если три члена пропорции известны, а четвёртый нужно найти, то говорят, что это задача на пропорцию. Задачи на пропорции возникают очень часто. Нужно только научиться уверенно их решать.
Мама дяди Фёдора из Простоквашино решила сварить для него яблочное варенье из 3 кг яблок. По рецепту на 2 кг яблок нужно 3 кг сахара. Сколько сахара понадобится маме дяди Фёдора для приготовления 3 кг варенья?
Сформулируем правило для нахождения неизвестного крайнего члена пропорции:
чтобы найти неизвестный крайний член пропорции, нужно произведение её средних членов разделить на известный крайний член пропорции.
Совершенно аналогично формируется правило для нахождения неизвестного среднего члена пропорции:
чтобы найти неизвестный средний член пропорции, нужно произведение её крайних членов разделить на известный средний член.
Найдите неизвестный член пропорции:
Итак, сегодня на уроке мы узнали, что такое пропорция. Познакомились с её основным свойством. Научились решать пропорции. А также, научились отвечать на вопрос, является ли данная пропорция верной.
Видеоурок по математике «Задачи на пропорцию». Часть 1.
Условие 1-й задачи: Шесть метров ткани стоят 1200 рублей. Сколько стоят четыре метра ткани?
Пропорция. Основное свойство пропорции. Задачи на пропорцию. Прямая и обратная зависимость.
Условие 2-й задачи: Пять комбайнов смогут убрать пшеницу с поля за 12 дней. За сколько дней уберут это поле три комбайна?
Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями!
 | Образцы всероссийских проверочных работ (ВПР) на 2022 год |
 | Минпросвещения планирует обновить федеральный перечень учебников |
 | «Молодые профессионалы»: среднее профессиональное образование должно стать востребованным |
 | Сергей Кравцов рассказал о проекте по обновлению правил русского языка |
 | В Министерстве просвещения разработали меморандум по воспитательной работе в школах |
Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьими лицами.
Администрация сайта готова оказать поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены 
Что такое пропорция
Что такое пропорция
Пропорция — это равенство двух отношения.
Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.
Пропорция всегда содержит равные коэффициенты.
Если выразить определение формулой, то выглядеть оно будет так:
a и d — крайние члены пропорции, b и с — средние члены пропорции.
Читается это выражение так: a так относится к b, как c относится к d
Например:
Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.
15 и 3 — крайние члены пропорции.
5 и 9 — средние члены пропорции.
Наглядный пример для понимания:
У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.
Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!
А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.
Что мы имеем: 4 кусочка и 2 друга, претендующих на них.
Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.
Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.
Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным😉
Основное свойство пропорции
Запомните основное свойство пропорции:
Произведение крайних членов пропорции равно произведению средних членов этой пропорции.
В виде формулы свойство выглядит так:
a : b = c : d
a * d = b * c
Мы знаем, что a и d — крайние члены пропорции, b и c — средние.
Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.
Давайте проверим несколько пропорций.
Пример 1. Дана пропорция:6/2 = 12/4
Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.
Пример 2. Дана пропорция: 10/2 = 16/4
Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Примеры решения задач с пропорцией
Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.
Задачка 1. Дана математическая пропорция: 15/3 = x/4
Ответ: в пропорции 15/3 = x/4, x = 20
Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.
Ответ: четвертый член пропорции — 12.
Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?
Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.
Задачка 4. Дана пропорция: 20/2 = y/4