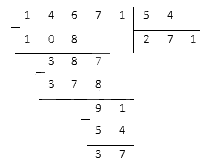Как решать примеры с остатком

Деление в столбик

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Как правильно делить в столбик

Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который впоследствии будет срабатывать автоматически.

Рассмотрим пример деления трехзначного числа на однозначное 322 : 7. Для начала определимся с терминами:

Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.

Шаг 2. Смотрим на делимое слева направо и находим ту часть, которая больше делителя. 3, 32 или 322? Нам подходит 32. Теперь нужно определить сколько раз наш делитель 7 содержится в числе 32. Похоже, что четыре раза.

Проверяем: 4 × 7 = 28, а 28

Шаг 3. Остаток равен 4. Для продолжения решения его нужно увеличить. Мы сделаем это за счет следующей цифры делимого. Приписываем к четверке оставшуюся двойку и продолжаем размышлять.

Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем полученное число к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.

Мы закончили решать пример и в результате получили целое число 46.

Как выглядит деление в столбик с остатком

Это такое же деление, только в результате получается неровное число, как получилось в примере выше.

Примеры на деление в столбик

Давайте закрепим знания на практике. Для этого разделите столбиком примеры ниже, а после проверьте полученные цифры — чур, не подглядывать!

Источник

Математика

Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет

С этой картой можно накопить на мечту, жми ⇒

План урока:

Здравствуйте, ребята. Я, Знайка, продолжаю учить вас математике.

Выражение «твердый орешек» означает трудную для решения задачу. Орешек знанья тверд, но мы не привыкли отступать, вместе его расколем. Пусть скорлупа ореха — символ знания, ядро — опыт человечества. Математика раскроет тайны деления двузначных чисел, если будем стараться. Французский ученый Декарт говорил: «Умейте использовать свой хороший ум, чтобы справиться с задачами».

Случаи деления 80 : 20, 87 : 29

Начнем с деления на двузначное число.

Приемы деления вида 80 : 20

Приемы деления вида 87 : 29

Найдите значения двух выражений:

Для решения посмотрите на цифры единиц. Делитель заканчивается на 9. Вспомните таблицу умножения девяти. Какое произведение имеет семерку на конце? 27.

Других вариантов в таблице умножения на девять нет. Ответ равен трем.

Внимательно посмотрите на цифры в единицах. Делимое заканчивается на четверку. Вспомните множитель, который при умножении шести в произведении дает последнюю цифру четверку.

Это два случая: четыре, девять. В значениях произведений четверка на конце. Какой множитель подходит? Давайте посмотрим. Девять — многовато.

Задания легко решать, если знаешь таблицу умножения.

Деление столбиком на двузначное число

Вы уже знаете, что для записи действия деления применяют математический символ в виде двоеточия (∶), обелюса (÷), дробной (–), косой (∕) черты. Сегодня мы используем знак, который похож на лежащую боком букву.

При делении столбиком очень важна аккуратность, поэтому возьмите листок в клеточку.

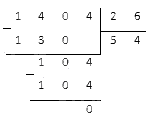
Как записать решение примера 32 : 16 столбиком? Запишите каждую цифру делимого 32 в отдельную клеточку. Отступите одну клеточку вправо, запишите делитель 16. Проведите вертикальную и горизонтальную черточку.

Подбираем частное. Посмотрите на цифры единиц 2 и 6. Вспомните табличные случаи.

Семерка нам не подойдет, потому что 16 ∙ 7 — это большая величина. Значит, выбираем двойку. Проверяем: 16 ∙ 2 = 32. Записываем двойку на место частного под чертой. Вычитаем 32 из делимого. Пишем нуль. 32 разделили нацело.

Хорошо. А знаете ли вы, что с древних времён замечено влияние грецкого ореха на работу мозга. Как будто природа создала его, по форме извилин напоминающим полушария головного мозга. Благодаря работе этого центрального органа мы справляемся с математическими задачами.

Деление с остатком

Ребята, я предлагаю вам отправиться в путешествие по реке на лодках. Прежде чем отплыть от берега, нам нужно разделить 9 спасательных кругов на 2 лодки. Как узнать, сколько кругов окажется в одной лодке?

Верно, надо разделить. Запишите решение. Сколько получилось в выражении?

У вас трудности. Что заметили?

9 на 2 нацело не делится.

Почему не можем найти значение данного выражения?

Потому что это не табличный случай. Мы не умеем решать такие выражения.

Ребята, оказывается, в примерах может получиться остаток. Это арифметическое действие, играющее большую роль в математике и криптографии — науке о защите информации. В компьютерной технике тоже часто решают данные выражения.

Напишите отрезок натурального ряда от 17 до 37.

Выпишите из этого отрезка числа, которые делятся на 9.

Проверьте, это — 18, 27, 36.

Остаток при делении натуральных чисел 19, 28, 37 на 9 равен единице, потому что они следующие при счете.

Запишите отрезок натурального ряда от 11 до 25. Обведите числа, которые делятся на шесть нацело.

Укажите остатки при делении на 6 тринадцати и четырнадцати. Запишите выражения.

Проверьте:

Объясните, как рассуждали.

15 — на третьем месте после 12, 16 — четвертое место, а 17 – пятое место после 12.

Какой самый большой остаток получается при делении на 6?

Это пять, так как между величинами, которые делятся на шесть нацело, находится пять чисел.

Интересно знать! В Древнем Египте кушать ядра грецких орехов могли только высшие, самые главные жрецы. Для всех остальных, особенно для простого народа — это было запрещено. Чтобы не становились умнее и не начали много думать. Но мы с вами знаем пользу орехов и хорошо соображаем, поэтому продолжаем урок.

Деление с остатком на однозначное число

Существует два способа решения примеров.

1 способ деления на 5, 6, 7, 8, 9

Первый способ подходит, когда делитель равен или больше пяти. Мы должны найти в делимом наибольшее число, чтобы разделить, например, на семерку.

Как его отыскать? Посчитайте семерками. Если бы делили на пять, то считали бы пятерками, на шесть – шестерками и так далее.

Разве 41 разделить на 7 — это пять? Нет, мы разделили только 35. Теперь найдем, сколько не разделили. Из 41 отнимите 35, получится шесть. Это искомый остаток.

Сделайте обязательный шаг — убедитесь, что остаток получился меньше чем делитель. Действительно 6 1 2

Источник

Деление целых чисел с остатком: правила, примеры

Статья разбирает понятие деления целых чисел с остатком. Докажем теорему о делимости целых чисел с остатком и просмотрим связи между делимыми и делителями, неполными частными и остатками. Рассмотрим правила, когда производится деление целых чисел с остатками, рассмотрев подробно на примерах. В конце решения выполним проверку.

Общее представление о делении целых чисел с остатками

Деление целых чисел с остатком рассматривается как обобщенное деление с остатком натуральных чисел. Это выполняется потому, что натуральные числа – это составная часть целых.

Остаток при делении чисел a на b возможен нулевой, тогда говорят, что a делится на b нацело, то есть без остатка. Деление без остатка считается частным случаем деления.

Если делим ноль на некоторое число, получаем в результате ноль. Остаток деления также будет равен нулю. Это можно проследить из теории о делении нуля на целое число.

Теперь рассмотрим смысл деления целых чисел с остатком.

Известно, что целые положительные числа – натуральные, тогда при делении с остатком получится такой же смысл, как и при делении натуральных чисел с остатком.

Деление любого числа а на целое не имеет смысла, но возможно как вариант.

Теорема о делимости целых чисел с остатком

Доказательство единственности

Связь между делимым, делителем, неполным частным и остатком

Деление с остатком целых положительных чисел, примеры

Все целые положительные числа являются натуральными. Отсюда следует, что деление выполняется по всем правилам деления с остатком натуральных чисел. Скорость выполнения деления с остатком натуральных чисел важна, так как на нем основано не только деление положительных, но и правила деления целых произвольных.

Самый удобный метод деления – это столбик, так как проще и быстрее получить неполное или просто частное с остатком. Рассмотрим решение более подробно.

Данное деление необходимо выполнять столбиком:

Правило деления с остатком целого положительного числа на целое отрицательное, примеры

Чтобы выполнить деление с остатком положительного числа на целое отрицательное, необходимо сформулировать правило.

Отсюда имеем, что неполное частное от деления целого полодительного числа на целое отрицательное число считают целым неположительным числом.

Рассмотрим на примере алгоритма деления целого положительного числа на целое отрицательное.

Ответ: 17 : ( − 5 ) = − 3 (ост. 2 ).

Деление с остатком целого отрицательного числа на целое положительное, примеры

Формулировка правила деления с остатком выглядит следующим образом.

Исходя из правила можно сделать вывод, что при делении получим целое неотрицательное число. Для точности решения применяют алгоритм деления а на b с остатком:

Рассмотрим на примере решения, где применяется данный алгоритм.

Ответ: ( − 17 ) : 5 = − 4 (ост. 3 ).

Необходимо произвести деление столбиком и по мудулю.

Правило деления с остатком целых отрицательных чисел, примеры

Необходимо сформулировать правило деления с остатком целых отрицательных чисел.

Отсюда следует, что неполное частное от деления целых отрицательных чисел будет число положительное.

Сформулируем данное правило в виде алгоритма:

Данный алгоритм рассмотрим на примере.

Ответ: ( − 17 ) : ( − 5 ) = 4 (ост. 3 ).

Проверка результата деления целых чисел с остатком

Рассмотрим на примерах.

Выполнить проверку деления ( − 17 ) : 5 = − 3 (ост. − 2 ). Верно ли равенство?

Имеем, что второе условие выполненное, но недостаточное для данного случая.

Ответ: нет.

Отсюда следует вывод, что деление произведено с ошибкой.

Источник

Деление с остатком

Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.

Как делить с остатком?

Выполнить деление не всегда возможно, так как бывают случаи, когда одно число не делится на другое. Например, число 11 не делится на 3, так как нет такого натурального числа, при умножении которого на 3 получилось бы 11.

Когда деление невозможно выполнить условились делить не всё делимое, а только наибольшую его часть, какая только может разделиться на делитель. В данном примере наибольшая часть делимого, которая может быть разделена на 3 — это 9 (в результате получим 3), оставшаяся меньшая часть делимого — 2 не разделится на 3.

Говоря о делении 11 на 3, 11 по прежнему называется делимым, 3 — делителем, результат деления — число 3, называют неполным частным, а число 2 — остатком от деления. Само деление в этом случае называют делением с остатком.

Неполное частное — это наибольшее число, которое при умножении на делитель даёт произведение, не превосходящее делимого. Остаток — это разность между делимым и этим произведением. Остаток всегда меньше делителя, иначе его тоже можно было бы поделить на делитель.

Остаток всегда меньше делителя.

Деление с остатком можно записывать так:

где 27 — это делимое, 7 — делитель, 3 — неполное частное, а 6 — остаток.

Если при делении одного натурального числа на другое в остатке получается 0, то говорят, что первое число делится на второе нацело. Например, 4 делится на 2 нацело. Число 5 не делится на 2 нацело. Слово нацело обычно опускают для краткости и говорят: такое-то число делится на другое, например: 4 делится на 2, а 5 не делится на 2.

Пример. Выполнить деление с остатком:

Задание. Какие остатки могут получаться при делении на 3? на 6? на 8?

Решение: Так как остаток всегда меньше делителя то:

Проверка деления с остатком

где 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.

Чтобы узнать правильно ли было выполнено деление с остатком, можно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, равное делимому, то деление с остатком выполнено верно:

Источник

Деление с остатком

Содержание

И так, мы уже познакомились с тем, что же такое деление. Но есть еще один важный и нужный вид деления – это деление с остатком.

Представим, что мы купили 10 яблок. К нам пришли друзья и мы захотели поделиться с ними яблоками, и при этом дать каждому равное количество.

Если друга всего 2, то каждому дадим по 5 яблок; если их 5, то по 2; а если 10, то по одному.

Но что делать, если друзей будет 3, 7 или 9? Нам не получится разделить 10 яблок поровну на такое количество человек.

Откуда берется остаток

Предположим, что в итоге у нас 7 друзей и 10 яблок. Чтобы никого не обидеть, мы можем дать каждому по одному и у нас останется 3 яблока. Теперь давайте рассмотрим пример:

В данном случае, 10 яблок – это делимое, 7 друзей – делитель, а 1 – неполное частное. Что же означает цифра 3 и откуда она взялась?

То число, которое осталось при делении, называют остатком.

Соответственно, в нашем случае 3 яблока и будут остатком.

Как найти остаток

Рассмотрим другой пример:

Запомним еще 2 правила, которые необходимы при работе с остатком:

Остаток всегда меньше делителя.

Если остаток равен нулю, то говорят, что делимое делится на делитель без остатка, то есть нацело.

Как найти делимое

Нужно уметь находить не только частное и остаток, но и делимое. На самом деле, здесь также все просто.

Чтобы найти делимое при делении с остатком, нужно умножить неполное частное на делитель и к полученному произведению прибавить остаток.

Источник