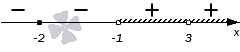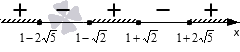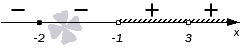Как решать неравенства дроби

Решение целых и дробно рациональных неравенств

Продолжаем разбирать способы решения неравенств, имеющих в составе одну переменную. Мы уже изучили линейные и квадратные неравенства, которые представляют из себя частные случаи рациональных неравенств. В этой статье мы уточним, неравенства какого типа относятся к рациональным, расскажем, на какие виды они делятся (целые и дробные). После этого покажем, как правильно их решать, приведем нужные алгоритмы и разберем конкретные задачи.

Понятие рациональных равенств

Когда в школе изучают тему решения неравенств, то сразу берут рациональные неравенства. На них приобретаются и оттачиваются навыки работы с этим видом выражений. Сформулируем определение данного понятия:

Рациональное неравенство представляет из себя такое неравенство с переменными, которое содержит в обоих частях рациональные выражения.

Таким образом, мы можем узнать рациональное неравенство, посмотрев на его запись. И с правой, и с левой стороны у него должны быть расположены рациональные выражения. Приведем примеры:

А вот неравенство вида 5 + x + 1 x · y · z не относится к рациональным, поскольку слева у него есть переменная под знаком корня.

Все рациональные неравенства делятся на целые и дробные.

Целое рациональное равенство состоит из целых рациональных выражений (в обеих частях).

Дробно рациональное равенство – это такое равенство, которое содержит дробное выражение в одной или обеих своих частях.

Мы разобрали, что из себя представляют рациональные неравенства, и выделили их основные типы. Можем переходить дальше, к обзору способов их решения.

Как решать целые неравенства

Начнем с перенесения выражения из правой части в левую. Получим следующее:

Зачастую такого простого преобразования будет достаточно для решения неравенства, поскольку в итоге может получиться линейное или квадратное неравенство, значение которого вычислить несложно. Разберем такие задачи.

Решение

Начнем с переноса выражения из правой части в левую с противоположным знаком.

x · ( x + 3 ) + 2 · x − ( x + 1 ) 2 − 1 ≤ 0

Решение

Переносим выражение из левой части в правую и выполняем дальнейшие преобразования с помощью формул сокращенного умножения.

( x 2 + 1 ) 2 − 3 · x 2 − ( x 2 − x ) · ( x 2 + x ) > 0 x 4 + 2 · x 2 + 1 − 3 · x 2 − x 4 + x 2 > 0 1 > 0

Ответ: любое действительно число.

Решение

Мы вывели квадратное неравенство, равносильное исходному, которое легко решить несколькими методами. Применим графический способ.

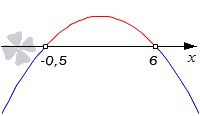
Начнем с вычисления корней квадратного трехчлена − 2 · x 2 + 11 · x + 6 :

Теперь на схеме отметим все необходимые нули. Поскольку старший коэффициент меньше нуля, ветви параболы на графике будут смотреть вниз.

Решение

Начнем, как всегда, с переноса выражения в левую часть, после чего нужно будет выполнить раскрытие скобок и приведение подобных слагаемых.

( x 2 + 2 ) · ( x + 4 ) − 14 + 9 · x 0 x 3 + 4 · x 2 + 2 · x + 8 − 14 + 9 · x 0 x 3 + 4 · x 2 + 11 · x − 6 0

В итоге преобразований у нас получилось равносильное исходному равенство, слева у которого стоит многочлен третьей степени. Применим метод интервалов для его решения.

Решение

Но есть и другие способы решения. Если мы перенесем выражения из правой части исходного неравенства в левую, то сможем выполнить вынесение за скобки общего множителя x 2 − 2 · x − 1:

Как решать дробно рациональные неравенства

Для таких случаев и добавлен последний шаг алгоритма. Выполнив его, вы избавитесь от посторонних значений переменной, которые возникают из-за расширения области допустимых значений. Возьмем несколько примеров, чтобы было более понятно, о чем идет речь.

Решение

После этого нам нужно преобразовать его так, чтобы было удобно применить метод интервалов. Первым делом приводим алгебраические дроби к наименьшему общему знаменателю ( x − 3 ) 2 · ( x + 1 ) :

Сворачиваем выражение в числителе, применяя формулу квадрата суммы:

Используем метод интервалов:

Решение

Переносим выражения из правой части в левую:

Далее выполняем преобразование левой части. Сначала преобразуем первую дробь:

Учитывая получившийся результат, запишем:

В заключение приведем еще один пример задачи, в котором окончательный ответ зависит от области допустимых значений.

Решение

Решений у этой системы нет, поскольку

Источник

Дробные рациональные неравенства

Дробные рациональные неравенства – это неравенства, в которых есть хотя бы одна дробь с переменной в знаменателе.

Как решать дробные рациональные неравенства:

Алгоритм решения дробно-рациональных неравенств.

Примеры:

Расставьте знаки на интервалах числовой оси. Напомню правила расстановки знаков:

— Дальше двигаемся влево;

— Переходя через число:

— меняем знак, если скобка с этим числом была в нечетной степени (\(1\), \(3\), \(5\)…)

— не меняем знак, если скобка с этим числом была в четной степени (\(2\), \(4\), \(6\)…)

Примеры:

Выделите нужные промежутки. Если есть отдельно стоящий корень, то отметьте его флажком, чтоб не забыть внести его в ответ (см. пример ниже).

Примеры:

Запишите в ответ выделенные промежутки и корни, отмеченные флажком (если они есть).

Переносим дробь из правой части в левую, меняя знак перед ней.

Вычитаем две дроби с одинаковым знаменателем.

Мы привели неравенство к нужному виду. Теперь решаем по алгоритму.

Сначала вычисляем те значения икса, которые сделают нулем числитель или знаменатель.

Отмечаем их на оси, не забывая «выколоть» иксы от знаменателя и закрасить те, что от числителя.

Расставляем знаки на других интервалах.
Обратите внимание, что в \(x=-1\) знак меняется, а в \(3\) и \(-2\) (выделены рамкой) – нет.
Точку \(-2\) отмечаем флажком, чтобы не забыть взять ее в ответ. Все. Нам подойдут интервалы с плюсом и точка \(-2\). Готово.

Неравенства нельзя умножать или делить на выражения с переменной, если неизвестен знак этого выражения.

Уравнения без проблем можно умножить/делить хоть на положительное число или выражение, хоть на отрицательное. И мы это постоянно делаем при решении уравнений.

Непонятно, мы же не знаем каким оно (выражение на которое умножали) было– положительным или отрицательным! Действительно, при иксе равном \(1\), значение \((x-3)\) отрицательно, а при иксе равном \(7\) – положительно. Поэтому так преобразовывать нельзя. При этом заметим, что:

Например, дробное рациональное неравенство \(\frac<(x-3)^2+5>\) \(≥0\) умножить на \((x-3)^2+5\) можно, потому что это выражение положительно при любом иксе (и значит, после умножения мы оставим тот же знак сравнения).

А вот неравенство \(\frac\) \(≥\) \(\frac<3-x>\) умножить на \((x+5)\) – нельзя, потому что при разных иксах его значение может быть и отрицательным, и положительным.

Источник

Дробно рациональные неравенства

Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).

Примеры дробно рациональных неравенств:

x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3

Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.

Алгоритм решения дробно рациональных неравенств:

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.

Примеры решения дробно рациональных неравенств:

№1. Решить неравенство x − 1 x + 3 > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.

Это значит, что знак на интервале, в котором лежит точка 2 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )

№2. Решить неравенство 3 ( x + 8 ) ≤ 5.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

3 ( x + 8 ) − 5 \ x + 8 ≤ 0

3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 x − 40 x + 8 ≤ 0

x = − 37 5 = − 37 5 = − 7,4

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.

− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )

№3. Решить неравенство x 2 − 1 x > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.

x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )

Если вас интересуют более сложные неравенства (с корнем чётной степени кратности, например), посмотрите видео «Метод интервалов: сложные случаи».

Спасибо за просмотр этого урока! Если у вас остались вопросы, напишите их в комментариях.

Источник

Дробно-рациональные неравенства

Соответствие между решениями целых рациональных неравенств и дробно-рациональных неравенств

Для решения целых рациональных неравенств следует раскладывать соответствующие многочлены на линейные множители, и затем использовать метод интервалов (см. §7 данного справочника).

Поэтому для решения дробно-рациональных неравенств применяются те же алгоритмы, что и для решения целых рациональных неравенств. Некоторые отличия возникают только в «цвете» точек на числовой прямой (о «цвете» точек, см. §7 данного справочника).

При решении строгих дробно-рациональных неравенств все точки, попадающие на числовую прямую как корни числителя и знаменателя – «белые».

При решении нестрогих дробно-рациональных неравенств все точки, попадающие на числовую прямую как корни числителя – «чёрные», а все точки, попадающие на числовую прямую как корни знаменателя – «белые» (т.к. знаменатель не может быть равен 0).

С учётом этого замечания, для решения дробно-рациональных и целых рациональных неравенств применяются одни и те же алгоритмы.

По условию дробь неотрицательная,$ \ge 0$. Выбираем промежутки, помеченные «+», учитываем цвет точек за счёт круглых и квадратных скобок:

$ x \in (-\infty;-2) \cup [3;+\infty)$

Примеры

Пример 1. Решите неравенства:

Раскладываем числитель и знаменатель на множители:

Выносим все корни из скобок на числовую прямую (все точки «белые»), определяем знаки промежутков:

Выбираем промежутки с «+».

Переносим всё в одну сторону, приводим к общему знаменателю:

Раскладываем числитель на множители:

Выбираем промежутки с «+».

Сравните решения, сделайте выводы.

Возвращаемся к исходной переменной:

Это – парабола ветками вверх. Точки пересечения с осью OX:(0;0)и (1;0)

Ось симметрии:$ x_0 = \frac <2>= \frac<0+1> <2>= \frac<1><2>$

В этой же системе координат строим уровни:

и отмечаем области:

Записываем решение – те x, для которых точки параболы попадают в заштрихованные области:

Источник

Рациональные неравенства (ЕГЭ 2022)

Хочешь без труда решать ЛЮБЫЕ неравенства?

Тогда начни с рациональных! Они станут твоей крепкой опорой в решении других неравенств.

Читай эту статью и ты во всём разберешься!

Рациональные неравенства — коротко о главном

Определение рационального неравенства

Рациональное неравенство — неравенство, левая и правая части которого являются дробно-рациональными функциями, то есть функциями, представимыми в виде отношения многочленов \(\displaystyle f\left(x\right)\) и \(\displaystyle g\left(x\right)\).

Стандартный вид рационального неравенства

Строгие рациональные неравенства

Рациональные неравенства — подробнее

Рациональные неравенства – это неравенства, обе части которых являются рациональными выражениями.

Что такое рациональное выражение? Напомню:

Рациональное выражение — это алгебраическое выражение, составленное из чисел и переменной \(\displaystyle x\) с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.

Например, такое рациональное неравенство: \(\displaystyle \frac<-2>\le \frac\)

Решение всех рациональных неравенств сводится к двум основным шагам:

Шаг 1. Перенос. Общий знаменатель. Разложение на множители

Переносим все в одну сторону, приводим к общему знаменателю и раскладываем числитель и знаменатель на множители.

Все множители должны быть «линейными», то есть переменная в каждом из них – только в первой степени.

Если какой-то из множителей нелинейный, и его невозможно разложить на линейные, от него надо избавиться.

Если забыл, как раскладывать выражение на множители, прочти тему «Разложение многочленов на множители».

Шаг 2. Метод интервалов

Если не знаешь, что это такое, прочти тему «Метод интервалов».

Первый шаг у нас уже раньше встречался. Где? В рациональных уравнениях!

Но в отличие от уравнений, в неравенствах мы никогда не разделяем числитель и знаменатель!

Более того, если в числителе и знаменателе есть одинаковые нечисловые множители, мы их не сокращаем!

Это правило у нас уже было в теме «Метод интервалов». И вообще, в этой теме мы уже учились решать рациональные неравенства. Поэтому здесь ограничимся отдельными примерами.

Источник