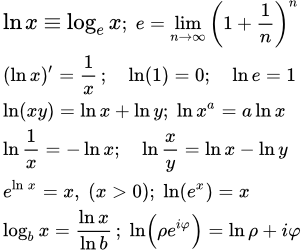Как решать натуральный логарифм
Натуральный логарифм, функция ln x
Определение
Исходя из определения, основанием натурального логарифма является число е:
е ≅ 2,718281828459045. ;
.
График натурального логарифма ln x
При x → 0 пределом натурального логарифма является минус бесконечность ( – ∞ ).
При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a растет быстрее логарифма.
Свойства натурального логарифма
Область определения, множество значений, экстремумы, возрастание, убывание
Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.
| Область определения | 0 |
| Область значений | – ∞ |
| Монотонность | монотонно возрастает |
| Нули, y = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | нет |
| + ∞ | |
| – ∞ |
Значения ln x
Основные формулы натуральных логарифмов
Формулы, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:
Доказательства этих формул представлены в разделе «Логарифм».
Обратная функция
Обратной для натурального логарифма является экспонента.
Производная ln x
Производная натурального логарифма:
.
Производная натурального логарифма от модуля x :
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
Выражения через комплексные числа
Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Логарифм. Натуральный логарифм.
За основание логарифмов нередко берут цифру е = 2,718281828. Логарифмы по данному основанию именуют натуральным. При проведении вычислений с натуральными логарифмами общепринято оперировать знаком ln, а не log; при этом число 2,718281828, определяющие основание, не указывают.
Само число е определяет предел монотонной ограниченной последовательности
Весьма часто для фиксации в памяти какого либо числа, цифры необходимого числа ассоциируют с какой-нибудь выдающейся датой. Скорость запоминания первых девяти знаков числа е после запятой возрастет, если заметить, что 1828 — это год рождения Льва Толстого!
На сегодняшний день существуют достаточно полные таблицы натуральных логарифмов.
График натурального логарифма (функции y = ln x) является следствием графика экспоненты зеркальным отражением относительно прямой у = х и имеет вид:
Натуральный логарифм может быть найден для каждого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a.
Элементарность этой формулировку, которая состыковывается со многими другими формулами, в которых задействован натуральный логарифм, явилось причиной образования названия «натуральный».
Если анализировать натуральный логарифм, как вещественную функцию действительной переменной, то она выступает обратной функцией к экспоненциальной функции, что сводится к тождествам:
По аналогии со всеми логарифмами, натуральный логарифм преобразует умножение в сложение, деление в вычитание:
Логарифм может быть найден для каждого положительного основания, которое не равно единице, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, обычно, определяются в терминах натурального логарифма.
Проанализировав график натурального логарифма, получаем, что он существует при положительных значениях переменной x. Он монотонно возрастает на своей области определения.
При x →0 пределом натурального логарифма выступает минус бесконечность ( –∞ ).При x → +∞ пределом натурального логарифма выступает плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a возрастает быстрее логарифма. Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумы у него отсутствуют.
Использование натуральных логарифмов весьма рационально при прохождении высшей математики. Так, использование логарифма удобно для нахождения ответа уравнений, в которых неизвестные фигурируют в качестве показателя степени. Применение в расчетах натуральных логарифмом дает возможность изрядно облегчить большое количество математических формул. Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
Натуральный логарифм — определение, свойства и примеры решений
Понятия и термины
Впервые упоминание о логарифмах встречается в античные времена. Толчком, послужившим для выделения понятия в отдельное выражение, стало открытие свойств степеней. Из-за стремительного развития архитектуры и строительства, астрономических исследований в средневековой Европе, Индии и Китае возник спрос на сложные расчёты. Так, вместо умножения при возведении в степень стали использовать логарифмирование — тождественную операцию.

В формуле log обозначает степенную функцию, n — основание, y — аргумент. Читается такая запись, как икс, равный логарифму игрек по основанию эн. В 1614 году шотландец Непер предложил таблицу логарифмов тригонометрических функций и описал их свойства. Несмотря на неточности в их вычислении, его расчёты вызвали восторг в математическом мире. Через пять лет английский учитель Спайделл внёс свои корректировки в таблицы и фактически предложил сборник натуральных логарифмов.
До начала XX века общепринятого обозначения выражения не существовало. Пока операция, заменяющая собой возведение в степень, не была подробно описана в книге «Введение в анализ бесконечных» Эйлера, который выделил и разделил все известные выражения логарифмов на три вида:
Использование в основании натурального логарифма математической константы e играет важную роль в математическом анализе. Иррациональное число принимается равным 2,71828. Её функция дифференцируется и интегрируется «в саму себя». Поэтому запись, в основании которой стоит такое число, и назвали натуральным.
Таким образом, логарифм, у которого по основанию находится постоянная e, называют также натуральным. Математически это определение записывают в виде выражения: ln c = loge c.
Функция выражения
Функцией натурального логарифма является график, описывающийся равенством y = ln x. Он представляет собой возрастающую кривую, находящуюся в четвёртом и первом квадранте декартовой системы координат. По своему виду функция обратна экспоненциальному изображению, принадлежащему выражению y = ex.
Первая производная логарифма равняется отношению единицы к основанию. Например, (log cx)’ = ((1/ln c) * ln x)’ = (ln x)’ / ln c = 1 / x * ln c. Так как основанием в натуральном выражении является экспонента, то учитывая свойства производной, итоговое равенство будет иметь вид: ln ex = 1 / x. Значение e определяется пределом, к которому стремится при неограниченном возрастании число m. То есть ограничение можно записать как (1 + 1 / m)m.

График натурально-логарифмической функции сходен с обычной, но имеет меньшую крутизну. К основным свойствам функции относят:
Формула ∫ ln p dp = p ln p — p + C является интегралом функции натурального логарифма. Выводится она с помощью метода интегрирования по частям: ∫ i dk = i * k — i dk. В заданном интеграле можно выделить функции i и k и отдельно выполнить их интегрирование. Тогда исходное выражение будет разложено на две части. Первая будет иметь вид: i = ln p, di = dp / p, а вторая — dk = dp, k = p. Соответственно, выполняя подстановку, можно записать следующее равенство: p ln p — ∫ dp = p ln p — p + C.
Иными словами, простая интегральная первообразная функция g (p) = f'(p) / f (x) будет иметь вид: ln |f (p)|. Это также следует из цепного правила и факта: d / dp (ln |p|) = 1/p. Последнее выражение можно переписать как ∫ dx / x = ln |x| + C, где свободный член — произвольная константа. В соответствии: ∫ f'(x) / f (x) dx =ln |f (x)| + C.
Свойства логарифма
Натуральное логарифмическое выражение характеризуется основной формулой сложения и вычитания. Согласно ей, функцию вида ln (x * y) справедливо преобразовать в сумму ln x + ln y. Аналогично, если в основании стоит знак деления, то его можно заменить разностью: ln (x/y) = ln x — ln y. Это свойство логарифма используется довольно часто при преобразованиях сложных уравнений.
Кроме этого, можно выделить следующие основные формулы, использующиеся при решениях заданий различной сложности:

Рассматриваемый логарифм можно разложить в степенной ряд. В нём слагаемыми служат действительная функция p © и её производные, делённые на факториал. Это преобразование называют разложение Маклорена. Для натурального выражения оно будет иметь вид: ln (1+c) = c — c2 /2 + c3 /3 — …+ (-1)n+1 * cn / n +…, при условии, что значение икса по модулю меньше единицы.
Учитывая, что аргумент однозначно не определён, то u = u0 + 2 pn, где n — простое целое число, то p = q * ei*u. Смысл этой записи в том, что натуральное выражение, рассматриваемое как функция, будет неоднозначное.
Примеры типовых заданий

Знание теоретических основ позволяет довольно легко вычислять натуральные выражения практически любой сложности. Самые простые задания даются для закрепления основных формул. Поэтому они обычно состоят из нескольких шагов. Например, нужно вычислить выражение: ln 2 * e2 + ln 1/ (2* e). Применяя свойство степеней, заданное выражение можно привести к виду: ln (2 * e 2 * 1 / (2 * e). После сокращения числителя и знаменателя на 2 * e, исходное выражение станет равным ln e. Таким образом, ln 2 * e2 + ln 1/ (2* e) = ln e = 1.
Вот ещё один простой пример. Пусть нужно решить равенство: logp e = ¼. В первую очередь следует определить допустимые значения. Эта область будет лежать в границах от нуля до бесконечности при p > 0 и от единицы до плюс бесконечности p ≠ 0. Используя свойство замены основания, левую часть логарифма можно преобразовать к виду натурального выражения: 1 / ln p = ½. Это выражение тождественно ln p = 2. Учитывая определение логарифма, ответом на задачу будет: p = e2.
При нахождении логарифмов в реальных условиях довольно часто приходится сталкиваться с громоздкими вычислениями. Такие расчёты требуют внимания и скрупулёзности. Ведь даже небольшая ошибка в итоге может привести к неправильному результату. При этом расчёт часто занимает продолжительное время.

В интернете существует несколько десятков сайтов, предоставляющих услуги по расчёту логарифмов онлайн. Это так называемые онлайн-калькуляторы. Доступ к ним может получить любой заинтересованный пользователь. Для этого ему просто понадобиться интернет и браузер с поддержкой Flesh технологи.
На страницах таких сервисов встроена специальная программа на языке Java. Фактически это аналог ранее популярных отдельных приложений, написанных на двоичном коде в Паскале. От пользователя требуется лишь вести в предложенную форму уравнение и нажать кнопку «Рассчитать». Приложение самостоятельно выберет нужные формулы и по ним рассчитает ответ.
Кроме конечного ответа, онлайн-сервисы предлагают подробный пошаговый расчёт. Это очень полезно для учащихся, которые пробуют разобраться в премудростях вычисления логарифма. А также для них на страницах предоставляется теоретический материал с примерами различной сложности. Примечательно и то, что доступ к сайтам обычно не только бесплатный, но и не требует какой-либо регистрации или указания личных данных.
По мнению пользователей рунета, из нескольких десятков существующих сайтов на русском языке можно выделить пятёрку лидеров:

Эти онлайн-калькуляторы имеют интуитивно понятный интерфейс и всю необходимую теорию для понятия принципа нахождения логарифма. Решив несколько заданий с их помощью, пользователь сможет самостоятельно вычислять любые логарифмические выражения. Таким образом, расчётчики смогут как подтянуть знания, так и проверить полученный ответ. Ведь появление ошибки при использовании программы практически невозможно.
Логарифмы и их свойства
Обычно определение логарифма дают очень сложно и запутанно. Мы постараемся сделать это очень просто и наглядно.
Для того, чтобы разобраться, что такое логарифм, давайте рассмотрим пример:
Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.
Теперь при помощи этой таблицы введем понятие логарифма.
Логарифм от числа 32 по основанию 2 (\(log_<2>(32)\)) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:
Аналогично, глядя в таблицу получим, что:
Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.
Теперь дадим определение логарифма в общем виде:
Логарифмом положительного числа \(b\) по основанию положительно числа \(a\) называется степень \(c\), в которую нужно возвести число \(a\), чтобы получить \(b\)
Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:
Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:
Или логарифм шести по основанию 4:
На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!
Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм \(log_<4>(6)\). Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6ке:
Значит \(log_<4>(6)\) принадлежите промежутку от 1 до 2:
Как посчитать логарифм
Почему так? Это следует из определения показательной функций. Показательная функция не может быть \(0\). А основание не равно \(1\), потому что тогда логарифм теряет смысл – ведь \(1\) в любой степени это будет \(1\).
При этих ограничениях логарифм существует.
В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.
Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.
Теперь давайте разберем общий алгоритм вычисления логарифмов:
Давайте разберем на примерах.
Пример 1. Посчитать логарифм \(9\) по основанию \(3\): \(log_<3>(9)\)
Пример 2. Вычислить логарифм \(\frac<1><125>\) по основанию \(5\): \(log_<5>(\frac<1><125>)\)
Пример 3. Вычислить логарифм \(4\) по основанию \(64\): \(log_<64>(4)\)
Пример 4. Вычислить логарифм \(1\) по основанию \(8\): \(log_<8>(1)\)
Пример 5. Вычислить логарифм \(15\) по основанию \(5\): \(log_<5>(15)\)
Как понять, что некоторое число \(a\) не будет являться степенью другого числа \(b\). Это довольно просто – нужно разложить \(a\) на простые множители.
\(16\) разложили, как произведение четырех двоек, значит \(16\) будет степенью двойки.
Разложив \(48\) на простые множители, видно, что у нас есть два множителя \(2\) и \(3\), значит \(48\) не будет степенью.
Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.
Десятичный логарифм
Натуральный логарифм
Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.
У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.
Свойства логарифмов
Давайте разберем несколько примеров на свойства логарифмов.
Пример 8. Воспользоваться формулой \(3\). Логарифм от произведения – это сумма логарифмов.
Пример 9. Воспользоваться формулой \(4\). Логарифм от частного – это разность логарифмов.
Пример 10. Формула \(5,6\). Свойства степени.
Логично, что будет выполняться и такое соотношение:
Пример 11. Формулы \(7,8\). Переход к другому основанию.
Десятичные и натуральные логарифмы
п.1. Десятичный логарифм и его свойства
Основание десятичных логарифмов \(10\gt 1\), поэтому они обладают всеми свойствами логарифмов с основанием больше единицы (см. §30 данного справочника).
Но у десятичных логарифмов есть также целых ряд дополнительных свойств, благодаря которым в докомпьютерную эпоху они широко использовались для трудоемких вычислений. Роль калькулятора тогда выполняли логарифмическая таблица и логарифмическая линейка.
| Число b | Стандартный вид | Характеристика | Мантисса b | Унифицированная запись | Логарифм числа \(\lg b\) |
| 420 | 4,2·10 2 | 2 | 0,623 | 2,623 | 2,623 |
| 42 | 4,2·10 1 | 1 | 0,623 | 1,623 | 1,623 |
| 4,2 | 4,2 | 2 | 0 | 0,623 | 0,623 |
| 0,42 | 4,2·10 –1 | –1 | 0,623 | \(\overline<1>,623\) | –0,377 |
| 0,042 | 4,2·10 –2 | –2 | 0,623 | \(\overline<2>,623\) | –1,377 |
Если использовать унифицированную запись, как в представленной таблице, то мантисса всегда лежит в промежутке \(0\lt \lg a\lt 1\). У чисел, отличающихся только порядком, мантисса одинакова. Можно составить таблицы мантисс и пользоваться ими для умножения и деления, «разбавляя» их несложным сложением и вычитанием целых характеристик по необходимости.
Первые таблицы логарифмов были изданы в 1617 году оксфордским математиком Бригсом. Таблицы пересчитывались, дополнялись и переиздавались вплоть до 70-х гг. ХХ века, когда на столах стали появляться калькуляторы.
Таблицы Брадиса, которыми по традиции пользуются наши школьники с 1921 года, издаются до сих пор и постепенно перекочевывают в Интернет.
Непосредственная связь десятичных логарифмов с десятичной системой исчисления делает их удобным инструментом для оценки порядка числа и сравнения чисел.
В практике приближенных вычислений используется следующая оценочная таблица:
Относительная погрешность этих приближений (кроме \(\lg 3)\) \(\delta\sim 0,5\text<%>\)
Например:
Сравним \(\log_23\) и \(log_58\)
Сравнивая с помощью оценки, получаем: \begin
п.2. Натуральный логарифм и его свойства
Основание натуральных логарифмов e>1, поэтому они обладают всеми свойствами логарифмов с основанием больше единицы (см. §30 данного справочника).
Для приближенного вычисления значения натурального логарифма используется «ряд Меркатора»:
Например:
С точностью до первого слагаемого: \(\ln 1,3=\ln(1+0,3)\approx 0,3\)
До второго слагаемого: \(\ln 0,3\approx 0,3-\frac<0,3^2><2>=0,255\)
До третьего слагаемого: \(\ln 0,3\approx 0,3-\frac<0,3^2><2>+\frac<0,3^3><3>=0,264\) и т.д.
Натуральные логарифмы настолько распространены в различных областях научных исследований, что когда вообще речь заходит «логарифмах», по умолчанию подразумевают именно их. Если же у вас в работе какие-то другие «логарифмы» (по основанию 2 или 10, например), это нужно уточнять.
п.3. Примеры
Пример 1. Найдите \(x\):
a) \( \lg x=2\lg a+\lg 7 \)
\(\lg x=\lg a^2+\lg 7=\lg(7a^2)\)
\(x=7a^2\)
Пример 2. Прологарифмируйте по основанию 10:
a) \(x=\frac<3a^2\sqrt[3]
Расчет относительной погрешности приближения на границах окрестностей \(|x|\lt 0,1\) и \(|x|\lt 0,2\) представлен в таблице: