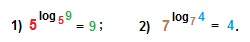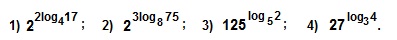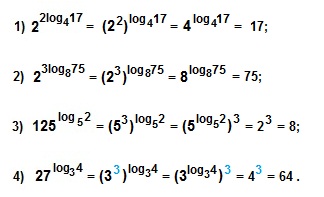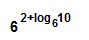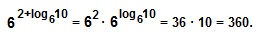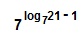Как решать логарифмические тождества

Логарифм. Основное логарифмическое тождество.

Основное логарифмическое тождество и логарифм тесно взаимосвязаны. И по сути, основное логарифмическое тождество является математической записью определения логарифма. Разберем подробно, что такое логарифм, откуда он произошел.

Когда, к примеру, в уравнении a x = b число а положительно, а число b отрицательно, то у такого уравнения корней нет. Но если только а и b положительны и а ≠ 1, то оно непременно имеет исключительно один единственный корень. Достаточно известный факт, что график показательной функции у = а х непременно пересекается с прямой у = b и притом исключительно в одной точке. Абсцисса точки пересечения и будут корнем уравнения.

Для обозначения корня уравнения a x = b принято употреблять log_ab (произносим: логарифм числа b по основанию а).

Логарифм числа b по основанию а это показатель степени, в которую нужно возвести число а, чтобы получить число b причем a > 0, a ≠ 1, b > 0.

Исходя из определения, получаем основное логарифмическое тождество:

Следствием основного логарифмического тождества является нижеследующее правило.

Из равенства двух вещественных логарифмов получаем равенство логарифмируемых выражений.

Действительно, когда log_ab = log_aс, то , откуда, b = c.

Рассмотрим, почему для логарифмического тождества взяты ограничения a > 0, a ≠ 1, b > 0.

Первое условие a ≠ 1.

Общеизвестно, что единица в любой степени будет единица, и равенство x = log_ab может существовать лишь при b = 1, но при этом log₁1 будет любым действительным числом. Для недопущения этой неоднозначности и принимается a ≠ 1.

Обоснуем необходимость условия a > 0.

При a = 0 по определению логарифма может существовать только при b = 0. И следовательно тогда log₀0 может быть любым отличным от нуля действительным числом, так как нуль в любой отличной от нуля степени есть нуль. Не допустить эту неоднозначность дает условие a ≠ 0. А при a 0.

И заключительное условие b > 0 является следствием из неравенства a > 0, так как x = log_ab, а значение степени с положительным основанием a всегда положительно.

Источник

11.4.2. Примеры на основное логарифмическое тождество

Это основное логарифмическое тождество.

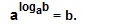
Это тождество следует из определения логарифма: так как логарифм – это показатель степени (n), то, возводя в эту степень число а, получим число b.

Вычислить:

При решении используем формулу возведения степени в степень: (a m ) n =a mn =(a n ) m и основное логарифмическое тождество.

Найти значение выражения:

Используем формулу произведения степеней с одинаковыми основаниями: a m ∙a n =a m + n

и основное логарифмическое тождество.

Найти значение выражения:

Используем формулу частного степеней с одинаковыми основаниями: a m :a n =a m — n

Источник

Логарифмы

Определение логарифма

Понятие логарифма и основного логарифмичесгого тождества

Понятие логарифма и основного логарифмическое тождества состоят в тесной зависимости, т.к. определение логарифма в математической записи и является основным логарифмическим тождеством.

Основное логарифмическое тождество вытекает из определения логарифма:

Логарифмом называют показатель степени n, при возведении в которую числа а получают число b.

Показательное уравнение a^n=b при a > 0, a ne 1 не имеет решений при неположительном b и имеет единственный корень при положительном b. Этот корень называется логарифмом числа b по основанию а и записывают:

Основное логарифмическое тождество

4 log₂ 7 =2 2 log₂ 7 = (2 log₂ 7 ) 2 = 7 2 = 49

2 1 + log₂ 7 = 2 · 2 log₂ 7 = 2 · 7 = 14

Что такое логарифм и как его посчитать

Логарифм имеет следующий вид:

где a – это основание логарифма,

b – это аргумент логарифма

Чтобы узнать значение логарифма приравняем его к X. и преобразовываем в и преобразовываем в Запомните, что именно основание (оно выделено красным) возводится в степень.

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!

Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:

Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.

Два очевидных следствия определения логарифма

log a 1 = 0 ( a > 0, a ≠ 1 )

Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень – единицу.

Логарифм. Свойства логарифма (корень логарифма, смена основания).

Корень логарифма из положительного числа равен логарифму подкоренного выражения, деленному на показатель корня/Логарифм. Свойства логарифма (корень логарифма, смена основания).

Использование свойств логарифмов при решении логарифмических уравнений и неравенств

Для того, чтобы не ошибаться при решении логарифмических уравнений и неравенств, свойства логарифмов, перечисленные в предыдущем разделе, следует применять внимательно и аккуратно.

Например, если при решении уравнения или неравенства требуется преобразовать выражение

следует применять формулу

поскольку в противном случае можно потерять корни.

По той же причине при преобразовании выражений

log_a ( f (x) g (x)) и

следует использовать формулы:

Степень можно выносить за знак логарифма

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

log a ( f ( x ) 2 = 2 log a f ( x )

Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть – только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.

Логарифмы со специальным обозначением

Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.

Виды логарифмов

log_a b – логарифм числа b по основанию a ( a > 0, a ≠ 1, b > 0)

lg b – десятичный логарифм (логарифм по основанию 10, a = 10).

Сумма логарифмов. Разница логарифмов

Логарифмы с одинаковыми основаниями можно складывать: Логарифмы с одинаковыми основаниями можно вычитать: Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!

Вынесение показателя степени из логарифма

Вынесение показателя степени из логарифма:

Переход к новому основанию

Когда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.

Разберем на примере.

Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:

Теперь применим переход к новому основанию для второго логарифма: Подставим полученные результаты в исходное выражение:

Десятичные и натуральные логарифмы

Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log₁₀x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например,

lg ( x y ) = lg x + lg y ( x > 0, y > 0 )

Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e – иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам:

log a b = lg b lg a = ln b ln a ( a > 0, a ≠ 1, b > 0 )

Вычисление логарифма равносильно решению показательного уравнения

при условии a > 0, a ≠ 1; b > 0, где

при условии a > 0, a ≠ 1; b > 0, где

Найти логарифм: log ₄ 8

Обозначим log₄ 8 через x :

Перейдем к показательному уравнению:

Сведем показательное уравнение к основе 2 и решим его:

Найти x если : log _x 125 = 3 2

За определением логарифма имеем:

x = (5 3 ) 2/3 = 5 3·2/3 = 5 2 = 25

Формулировки и доказательства свойств

Покажем примеры использования свойства логарифма произведения: log₅(2·3)=log₅2+log₅3 и .

Приведем пример использования этого свойства логарифма: .

Вот пример использования этого свойства: .

Покажем пару примеров применения этого свойства логарифмов: и .

Также часто используется формула , которая удобна при нахождении значений логарифмов. Для подтверждения своих слов покажем, как с ее помощью вычисляется значение логарифма вида . Имеем . Для доказательства формулы достаточно воспользоваться формулой перехода к новому основанию логарифма a : .

Осталось доказать свойства сравнения логарифмов.

Область допустимых значений (ОДЗ) логарифма

Теперь поговорим об ограничениях (ОДЗ – область допустимых значений переменных).

Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:

Поэтому и отрицательные основания проще выбросить, чем возиться с ними.

Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. Например, не существует, так как ни в какой степени не будет отрицательным числом (и даже нулем, поэтому тоже не существует).

В задачах с логарифмами первым делом нужно записать ОДЗ. Приведу пример:

Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Почему? Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?

– это явно неверно, так как основание не может быть отрицательным, то есть корень – «сторонний».

Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:

10 примеров логарифмов с решением

1. Найти значение выражения 2. Найти значение выражения 3. Найти значение выражения 3. Найти значение выражения 4. Найти значение выражения 5. Найти значение выражения 5. Найти значение выражения 6. Найти значение выражения Сначала найдем значение Сначала найдем значение Для этого приравняем его к Х:Тогда изначальное выражение принимает вид:

7. Найти значение выражения 7. Найти значение выражения Преобразуем наше выражение: Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выражения 8. Найти значение выражения Так как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов: 9. Найти значение выражения 9. Найти значение выражения Так как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:

10. Найти значение выражения Обращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄: Обращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄:

Надеюсь, теперь вы разобрались, что такое логарифм.

Источник