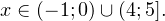Как решать логарифмические функции
Как решать логарифмические функции
График функции имеет следующий вид:
Рассмотрим свойства функции:
Примеры решения задач
Задание 1.
В одной координатной плоскости построить графики функций:
Решение.
Для начала построим график функции y = log2x. Для этого найдем значения функции при x = 


| x |  |  |  | 1 | 2 | 4 | 8 |
| y(x) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует и большее значение функции у. Функция y = log2x возрастает на всей области определения D(y)=R+, так как основание функции 2 > 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать только положительные значения (D(y) = R+), при этом значение у может быть любым (E(y) = R).
Графики всех данных функций пересекают ось Оx в точке (0; 1), так как логарифм по любому основанию от единицы равен нулю. C осью Оy графики не пересекаются, так как логарифм по положительному основанию не может быть равен нулю.
Чем больше основание a (если a > 1) логарифмической функции y = logax, тем ближе расположена кривая к оси Оx.
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
Задание 2.
В одной координатной плоскости построить графики функций:
Решение.
Для начала построим график функции 



| x |  |  |  | 1 | 2 | 4 | 8 |
| y(x) | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует меньшее значение функции y. Функция 
Подобным образом построим графики остальных функций.
Переменная х может принимать только положительные значения (D(y) = R+), при этом значение у может быть любым (E(y) = R).
Графики всех данных функций пересекают ось Оx в точке (0; 1), так как логарифм по любому основанию от единицы равен нулю. С осью Оy графики не пересекаются, так как логарифм по положительному основанию не может быть равен нулю.
Чем меньше основание a (если 0
Все данные функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Задание 3.
Найти обасть определеления функции:
Решение
Область определения данной функции задается следующим неравенством:
Решим это линейное неравенство:
Логарифм определен, если подлогарифмическая функция является положительной, то есть искомая область определения: D(y): (x-1)(x+5) > 0.
Решим полученное уравнение методом интервалов. Для этого найдем нули каждого из сомножителей:
Наносим их на координатную прямую и определяем знак неравенства на каждом из полученных промежутков.
Что такое логарифмическая функция? Определение, свойства, решение задач
Раздел логарифмов занимает огромное значение в школьном курсе «Математического анализа». Задания для логарифмических функций построены на иных принципах, нежели задачи для неравенств и уравнений. Знание определений и основных свойств понятий логарифм и логарифмическая функция, обеспечат успешное решение типовых задач ЕГЭ.
Определение понятия логарифм
Прежде чем приступить к объяснению, что представляет собой логарифмическая функция, стоит обратиться к определению логарифма.
Разберем конкретный пример: а log a x = x, где a › 0, a ≠ 1.
Основные свойства логарифмов можно перечислить несколькими пунктами:
Логарифмирование
Логарифмированием называют математическую операцию, которая позволяет с помощью свойств понятия найти логарифм числа или выражения.
Функция логарифма и ее свойства
Логарифмическая функция имеет вид
Сразу отметим, что график функции может быть возрастающим при a › 1 и убывающим при 0 ‹ a ‹ 1. В зависимости от этого кривая функции будет иметь тот или иной вид.
Приведем свойства и способ построения графиков логарифмов:
Построить обе разновидности графиков очень просто, рассмотрим процесс на примере
Для начала необходимо вспомнить свойства простого логарифма и ее функции. С их помощью нужно построить таблицу для конкретных значений x и y. Затем на координатной оси следует отметить полученные точки и соединить их плавной линией. Эта кривая и будет являться требуемым графиком.
Очевидно, что обе линии являются зеркальным отражением друг друга. Построив прямую y = x, можно увидеть ось симметрии.
Для того, чтобы быстро найти ответ задачи нужно рассчитать значения точек для y = log2x, а затем просто перенести начала точки координат на три деления вниз по оси OY и на 2 деления влево по оси OX.
В качестве доказательства построим расчетную таблицу для точек графика y = log2(x+2)-3 и сравним полученные значения с рисунком.
Как видно, координаты из таблицы и точек на графике совпадают, следовательно, перенос по осям был осуществлен правильно.
Примеры решения типовых задач ЕГЭ
Большую часть тестовых задач можно разделить на две части: поиск области определения, указания вида функции по рисунку графика, определение является ли функция возрастающей/убывающей.
Для быстрого ответа на задания необходимо четко уяснить, что f(x) возрастает, если показатель логарифма а › 1, а убывает – при 0 ‹ а ‹ 1. Однако, не только основание, но и аргумент может сильно повлиять на вид кривой функции.
Задание 1
F(x), отмеченные галочкой, являются правильными ответами. Сомнения в данном случае вызывают пример 2 и 3. Знак «-» перед log меняет возрастающую на убывающую и наоборот.
Ответ: 3,4,5.
Задание 2
Ответ: 4.
Данные типы заданий считаются легкими и оцениваются в 1- 2 балла.
Задание 3.
Определить убывающая или возрастающая ли функция и указать область ее определения.
Так как основание логарифма меньше единицы, но больше нуля – функция от x является убывающей. Согласно свойствам логарифма аргумент также должен быть больше нуля. Решим неравенство:
Ответ: область определения D(x) – интервал (50; + ∞).
Задание 4.
Ответ: 3, 1, оси OX, направо.
Подобные задания классифицируются как средние и оцениваются в 3 – 4 балла.
Задание 5. Найти область значений для функции:
Из свойств логарифма известно, что аргумент может быть только положительным. Поэтому рассчитаем область допустимых значений функции. Для этого нужно будет решить систему из двух неравенств:
Итак, искомый промежуток находится в пределе интервала (-4; 8), при других x становится невозможным вычислить значение одного из данных логарифмических выражений.
Согласно свойствам логарифмической функции сумма логарифмов с одинаковым основанием равна логарифму произведения их аргументов.
Графиком функции y = – x 2 + 4x + 32 является парабола, схематический график которой представлен ниже.
Точка A является экстремумом графика, в ней y принимает наибольшее значение. Координаты точки A (m; n) вычисляются по формулам, приведенным на рисунке. Высчитаем n для заданной параболы.
Наибольшее значение ymax = 36. Так как основание логарифма в примере больше 1, то функция будет возрастающей, и достигнет наибольшего значения при максимальном аргументе. Узнаем максимум для F(y):
Наименьшего значения в конкретном примере нет, поэтому ОДЗ для f(x) = log3(x+4)+ log3(8-x) является следующий интервал (- ∞; 2log36).
Подобные задачи можно отнести к категории «сложно» и оценивать не менее 4 баллов за правильный ответ.
Логарифмические уравнения
Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.
Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.
При этом 0,\;a> 0,\;a\neq 1′ alt=’b> 0,\;a> 0,\;a\neq 1′ />.
Обратим внимание на область допустимых значений логарифма:
Основное логарифмическое тождество:
Основные формулы для логарифмов:
(Логарифм произведения равен сумме логарифмов)
(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)
Формула перехода к новому основанию:
Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.
Все это пригодится нам в решении логарифмических уравнений.
Простейшие логарифмические уравнения
Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.
Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при 0,\;a> 0,\;a\neq 1′ alt=’b> 0,\;a> 0,\;a\neq 1′ />.
Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.
2. Решите уравнение:
3. Решите уравнение:
Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.
4. Решите уравнение:
Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.
5. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
0\\ x^<2>-4> 0\\ x^<2>+x=x^<2>-4 \end
Ответ: –4.
Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Запишем решение как цепочку равносильных переходов.
Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.
ОДЗ:
0\\ x> 0\\ x\neq 1 \end
Теперь можно «убрать» логарифмы.
— посторонний корень, поскольку должно выполняться условие 0′ alt=’x> 0′ />.
ОДЗ уравнения: 0′ alt=’x> 0′ />
Вернемся к переменной х:
Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.
Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.
Вернемся к переменной х. Получим:
. Мы нашли все корни исходного уравнения.
Логарифмические уравнения могут встретиться вам и в задании №1 Профильного ЕГЭ по математике, и в задании №12. И если в задании №1 нужно решить простейшее уравнение, то в задаче 12 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.
Это полезно
В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.
Логарифмические уравнения и неравенства
Логарифмическим уравнениям и неравенствам в вариантах ЕГЭ по математике посвящена задача C3. Научиться решать задания C3 из ЕГЭ по математике должен каждый ученик, если он хочет сдать предстоящий экзамен на «хорошо» или «отлично». В данной статье представлен краткий обзор часто встречающихся логарифмических уравнений и неравенств, а также основных методов их решения.
Итак, разберем сегодня несколько примеров логарифмических уравнений и неравенств, которые предлагались учащимся в вариантах ЕГЭ по математике прошлых лет. Но начнет с краткого изложение основных теоретических моментов, которые нам понадобятся для их решения.
Логарифмическая функция
Определение
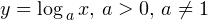
называют логарифмической функцией.
Основные свойства
Основные свойства логарифмической функции y = loga x:











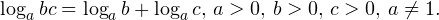 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>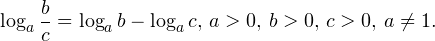 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>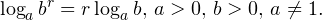 0,\, b>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>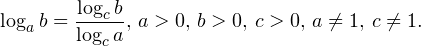 0,\, b>0,\, c>0,\, a\ne 1,\, c\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, c>0,\, a\ne 1,\, c\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>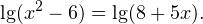
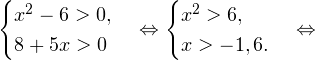 0, \\ 8+5x > 0 \end
0, \\ 8+5x > 0 \end 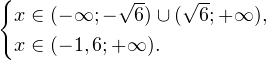
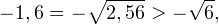 -\sqrt<6>, \]» title=»Rendered by QuickLaTeX.com»/>
-\sqrt<6>, \]» title=»Rendered by QuickLaTeX.com»/>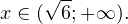
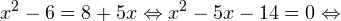
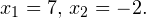
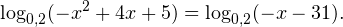
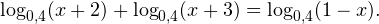
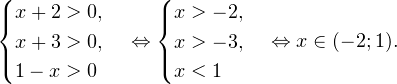 0, \\ x+3>0, \\ 1-x>0 \end
0, \\ x+3>0, \\ 1-x>0 \end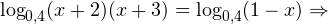
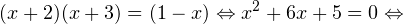
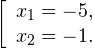
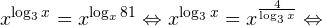
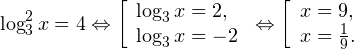
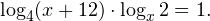
 0, \\ x>0, \\ x\ne 1 \end
0, \\ x>0, \\ x\ne 1 \end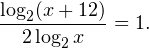
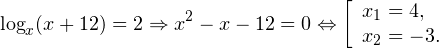
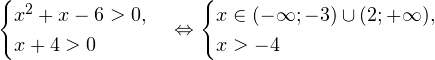 0, \\ x+4>0 \end
0, \\ x+4>0 \end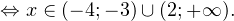
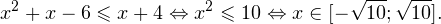
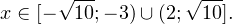
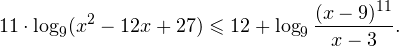
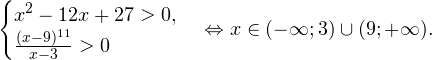 0, \\ \frac<(x-9)^<11>>
0, \\ \frac<(x-9)^<11>>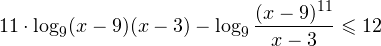
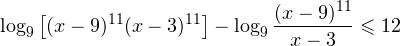
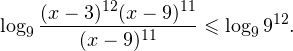
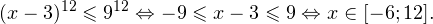
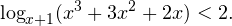
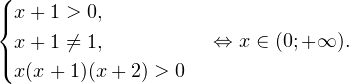 0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end
0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end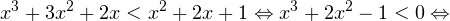
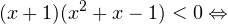
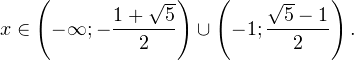
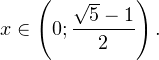
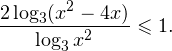
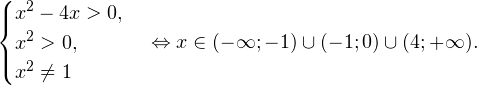 0, \\ x^2>0, \\ x^2\ne 1 \end
0, \\ x^2>0, \\ x^2\ne 1 \end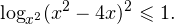
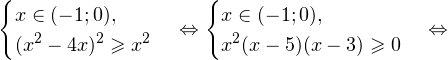
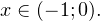
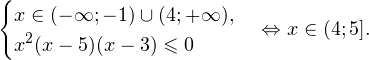
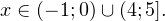
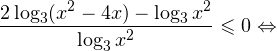
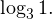 Это ничего не изменит, поскольку
Это ничего не изменит, поскольку 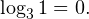
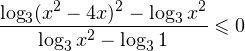
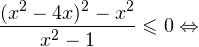
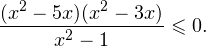
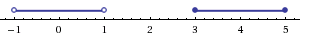
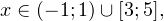 а с учетом области допустимых значений получаем тот же результат:
а с учетом области допустимых значений получаем тот же результат: