Как решать комплексные числа примеры

Комплексные числа

Формы

Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:

Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.

Изображение

Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:

Вычислить сумму и разность заданных комплексных чисел:

Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел:

Аналогично выполним вычитание чисел:

Выполнить умножение и деление комплексных чисел:

Так, теперь разделим первое число на второе:

Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки:

Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы:

Для возведения в квадрат достаточно умножить число само на себя:

Пользуемся формулой для умножения, раскрываем скобки и приводим подобные:

В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую.

Вычисляем значение модуля:

Найдем чем равен аргумент:

$$ \varphi = arctg \frac<3> <3>= arctg(1) = \frac<\pi> <4>$$

Записываем в тригонометрическом виде:

Преобразуем в алгебраическую форму для наглядности:

Представим число в тригонометрической форме. Найдем модуль и аргумент:

Используем знакомую формулу Муавра для вычисления корней любой степени:

Источник

Выражения, уравнения и системы уравнений
с комплексными числами

Сегодня на занятии мы отработаем типовые действия с комплексными числами, а также освоим технику решения выражений, уравнений и систем уравнений, которые эти числа содержат. Данный практикум является продолжением урока Комплексные числа для чайников, и поэтому если вы неважно ориентируетесь в теме, то, пожалуйста, пройдите по указанной выше ссылке. Ну а более подготовленным читателям предлагаю сразу же разогреться:

Решение: итак, требуется подставить в «страшную» дробь, провести упрощения, и перевести полученное комплексное число в тригонометрическую форму. Плюс чертёж.

Как лучше оформить решение? С «навороченным» алгебраическим выражением выгоднее разбираться поэтапно. Во-первых, меньше рассеивается внимание, и, во-вторых, если таки задание не зачтут, то будет намного проще отыскать ошибку.

…Да, такой вот Квазимодо от комплексных чисел получился…

Чтобы избавиться от дроби, умножим числитель и знаменатель на сопряженное знаменателю выражение. При этом в целях применения формулы разности квадратов следует предварительно (и уже обязательно!) поставить отрицательную действительную часть на 2-е место:

А сейчас ключевое правило:

НИ В КОЕМ СЛУЧАЕ НЕ ТОРОПИМСЯ! Лучше перестраховаться и прописать лишний шаг.
В выражениях, уравнениях и системах с комплексными числами самонадеянные устные вычисления чреваты, как никогда!

На завершающем шаге произошло хорошее сокращение и это просто отличный признак.

Примечание: строго говоря, здесь произошло деление комплексного числа на комплексное число 50 (вспоминаем, что ). Об этом нюансе я умалчивал до сих пор и о нём мы ещё поговорим чуть позже.

Обозначим наше достижение буквой

Представим полученный результат в тригонометрической форме. Вообще говоря, здесь можно обойтись без чертежа, но коль скоро, требуется – несколько рациональнее выполнить его прямо сейчас:

Вычислим модуль комплексного числа:

Если выполнять чертёж в масштабе 1 ед. = 1 см (2 тетрадные клетки), то полученное значение легко проверить с помощью обычной линейки.

Угол элементарно проверяется транспортиром. Вот в чём состоит несомненный плюс чертежа.

Таким образом: – искомое число в тригонометрической форме.

Выполним проверку:
, в чём и требовалось убедиться.

Незнакомые значения синуса и косинуса удобно находить по тригонометрической таблице.

Ответ:

Аналогичный пример для самостоятельного решения:

Постарайтесь не пропускать учебные примеры. Кажутся-то они, может быть, и простыми, но без тренировки «сесть в лужу» не просто легко, а очень легко. Поэтому «набиваем руку».

Краткое решение и ответ в конце урока.

Нередко задача допускает не единственный путь решения:

Делая дробь правильной, приходим к выводу, что можно «скрутить» 4 оборота ( рад.):

Как видите, одно «лишнее» действие. Желающие могут довести решение до конца и убедиться, что результаты совпадают.

В условии ничего не сказано о форме итогового комплексного числа, поэтому:

Ответ:

Но «для красоты» либо по требованию результат нетрудно представить и в алгебраической форме:

Краткое решение и ответ в конце урока.

Выражения – хорошо, а уравнения – лучше:

Уравнения с комплексными коэффициентами

Чем они отличаются от «обычных» уравнений? Коэффициентами =)

В свете вышеприведённого замечания начнём с этого примера:

Решение, в принципе, тоже можно оформить пошагово, но в данном случае овчинка выделки не стОит. Первоначальная задача состоит в том, чтобы упростить всё, что не содержит неизвестной «зет», в результате чего уравнение сведётся к виду :

Уверенно упрощаем среднюю дробь:

Результат переносим в правую часть и находим разность:

По правилу пропорции выражаем «зет»:

Теперь можно снова разделить и умножить на сопряжённое выражение, но подозрительно похожие числа числителя и знаменателя подсказывают следующий ход:

Ответ:

В целях проверки подставим полученное значение в левую часть исходного уравнения и проведём упрощения:

– получена правая часть исходного уравнения, таким образом, корень найден верно.

…Сейчас-сейчас… подберу для вас что-нибудь поинтереснее… держите:

Конечно же… как можно без него прожить:

Квадратное уравнение с комплексными коэффициентами

На уроке Комплексные числа для чайников мы узнали, что квадратное уравнение с действительными коэффициентами может иметь сопряжённые комплексные корни, после чего возникает закономерный вопрос: а почему, собственно, сами коэффициенты не могут быть комплексными? Сформулирую общий случай:

Квадратное уравнение с произвольными комплексными коэффициентами (1 или 2 из которых либо все три могут быть, в частности, и действительными) имеет два и только два комплексных корня (возможно один из которых либо оба действительны). При этом корни (как действительные, так и с ненулевой мнимой частью) могут совпадать (быть кратными).

Квадратное уравнение с комплексными коэффициентами решается по такой же схеме, что и «школьное» уравнение, с некоторыми отличиями в технике вычислений:

Найти корни квадратного уравнения

Решение: на первом месте расположена мнимая единица, и, в принципе, от неё можно избавиться (умножая обе части на ), однако, в этом нет особой надобности.

Для удобства выпишем коэффициенты:

Не теряем «минус» у свободного члена! …Может быть не всем понятно – перепишу уравнение в стандартном виде :

А вот и главное препятствие:

Применение общей формулы извлечения корня (см. последний параграф статьи Комплексные числа для чайников) осложняется серьёзными затруднениями, связанными с аргументом подкоренного комплексного числа (убедитесь сами). Но существует и другой, «алгебраический» путь! Корень будем искать в виде:

Возведём обе части в квадрат:

Два комплексных числа равны, если равны их действительные и их мнимые части. Таким образом, получаем следующую систему:

Систему проще решить подбором (более основательный путь – выразить из 2-го уравнения – подставить в 1-е, получить и решить биквадратное уравнение). Предполагая, что автор задачи не изверг, выдвигаем гипотезу, что и – целые числа. Из 1-го уравнения следуют, что «икс» по модулю больше, чем «игрек». Кроме того, положительное произведение сообщает нам, что неизвестные одного знака. Исходя из вышесказанного, и ориентируясь на 2-е уравнение, запишем все подходящие ему пары:

Очевидно, что 1-му уравнению системы удовлетворяют две последние пары, таким образом:

Не помешает промежуточная проверка:

что и требовалось проверить.

В качестве «рабочего» корня можно выбрать любое значение. Понятно, что лучше взять версию без «минусов»:

Находим корни, не забывая, кстати, что :

Ответ:

Проверим, удовлетворяют ли найденные корни уравнению :

Таким образом, решение найдено правильно.

По мотивам только что разобранной задачи:

Найти корни уравнения

А теперь можно расслабиться – в этом примере вы отделаетесь лёгким испугом 🙂

Решить уравнение и выполнить проверку

Решения и ответы в конце урока.

Заключительный параграф статьи посвящён

системе уравнений с комплексными числами

Расслабились и… не напрягаемся =) Рассмотрим простейший случай – систему двух линейных уравнений с двумя неизвестными:

Решить систему уравнений. Ответ представить в алгебраической и показательной формах, изобразить корни на чертеже.

Систему реально решить «детским» способом (выразить одну переменную через другую), однако гораздо удобнее использовать формулы Крамера. Вычислим главный определитель системы:

, значит, система имеет единственное решение.

Повторюсь, что лучше не торопиться и прописывать шаги максимально подробно:

Домножаем числитель и знаменатель на мнимую единицу и получаем 1-й корень:

Перед тем, как продолжать дальше, целесообразно проверить решение. Подставим найденные значения в левую часть каждого уравнения системы:

Получены соответствующие правые части, ч.т.п.

Представим корни в показательной форме. Для этого нужно найти их модули и аргументы:

1) – арктангенс «двойки» вычисляется «плохо», поэтому так и оставляем:

Ответ:

Решить систему уравнений

Найти произведение корней и представить его в тригонометрической форме.

Краткое решение совсем близко.

И в заключение ответим на экзистенциальный вопрос: для чего нужны комплексные числа? Комплексные числа нужны для расширения сознания выполнения заданий других разделов высшей математики, кроме того, они используются во вполне материальных инженерно-технических расчетах на практике.

На этом курс Опытного пользователя комплексных чисел завершён – сертификат вам на стену и новых достижений!

Пример 4: Решение:

Пример 6: Решение:

Умножим обе части уравнения на :

Ответ:

Проверка: подставим в исходное уравнение :

верное равенство;

верное равенство.
Что и требовалось проверить.

Пример 11: Решение: систему решим методом Крамера:

Таким образом, система имеет единственное решение.
Найдём произведение корней:

Представим результат в тригонометрической форме:

Ответ:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник

Введение в комлексные числа

Выяснив, что многие знакомые программисты не помнят комплексные числа или помнят их очень плохо, я решил сделать небольшую шпаргалку по формулам.

А школьники могут что-то новое узнать 😉
// Всех кого заинтересовал прошу под кат.

Итак, комплексные числа эта такие числа, которые можно записать как

Где x, y вещественные числа(т.е привычные всем числа), а i — число, для которого
выполняется равенство

x называется действительной частью, y — мнимой.

Это алгебраическая форма записи комплексного числа.

Существует также тригонометрическая форма записи комплексного числа z:

С введением, пожалуй, все.

Переходим к самому интересному — операциям над комплексными числами!
Для начала рассмотрим сложение.

У нас есть два таких комплексных числа:

Как же их сложить?
Очень просто: сложить действительную и мнимую части.
Получим число:

Все просто, не так ли?
Вычитание выполняется аналогично сложению.
Нужно просто вычесть из действительной части 1 числа действительную часть 2 числа,
а потом проделать тоже с мнимой частью.
Получим число

Умножение выполняется вот так:

Напомню, x это действительная часть, y — мнимая.
Деление выполняется вот так:

Кстати, поддержка комплексных чисел есть в стандартной библиотеке Python:

Вместо i используется j.
Кстати, это потому что Python принял конвенцию инженеров-электриков, у которых
буква i обозначает электрический ток.
Задавайте свой вопросы, если они есть, в комментариях.
Надеюсь, вы узнали для себя что-то новое.

UPD: В комментариях просили рассказать о практическом применении.
Так вот комплексные числа нашли широкое практическое применение в авиации
(подъемная сила крыла) и в электричестве.
Как видете, очень нужная вещь 😉

Источник

Основные действия над комплексными числами

Комплексные числа — определение и основные понятия

Обычные числа представляют собой множество действительных чисел, для обозначения которых используют букву R. Каждое число из множества можно отметить на числовой прямой.

К действительным числам носят:

Каждая точка на числовой прямой характеризуется некоторым действительным числом. Комплексное число является двумерным числом и записано в виде:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Где а и b являются действительными числами, i представляет собой так называемую мнимую единицу.

Уравнение можно мысленно поделить на несколько частей:

Следует отметить, что a + bi является единым числом, а не сложением. Места действительной и мнимой частей в уравнении можно менять:

Мнимую единицу допускается переставлять:

При таких операциях смысл выражения остается прежним. Однако стандартная запись комплексного числа имеет такой вид:

Данное утверждение можно привести в виде геометрической интерпретации. Тогда комплексные числа изображают на комплексной плоскости.

С помощью R обозначаю множество действительных чисел. В случае, когда требуется обозначить множество комплексных чисел, принято использовать букву С. Наличие буквы С на чертеже говорит о том, что на нем представлена комплексная плоскость. Данная плоскость включает две оси:

Re z — является действительной осью;

Im z — представляет собой мнимую ось.

Правила оформления такого графика практически не отличаются от требований к чертежам для декартовой системы координат. По осям задают масштаб и отмечают:

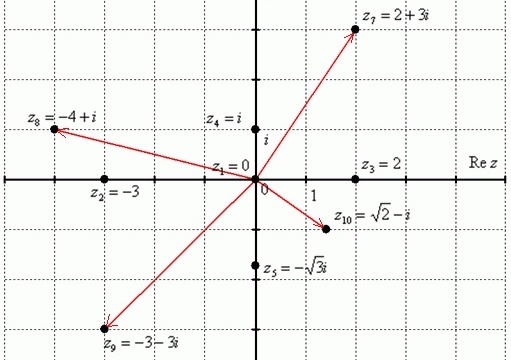
С помощью комплексной плоскости можно построить заданные комплексные числа:

Можно рассмотреть следующие комплексные числа:

Действительные числа являются частным случаем комплексных чисел. Действительная ось Re z обозначает в точности множество действительных чисел R, то есть на данной оси расположены все числа с обычными свойствами. Можно сформулировать справедливое утверждение: множество действительных чисел R представляет собой подмножество множества комплексных чисел С.

Данные числа являются комплексными числами, мнимая часть которых нулевая:

Мнимые числа с нулевой действительностью, которые расположены на мнимой оси Im z:

Есть ряд чисел с ненулевыми действительной и мнимой частью:

Для их обозначения используют точки на комплексной плоскости. К таким точкам проводят радиус-векторы из начала координат. Радиус-векторы не принято чертить к числам, которые расположены на осях и сливаются с ними.

Формы, как записываются

Алгебраическая запись комплексного числа имеет такой вид:

Кроме данной формы существует еще несколько способов для записи. Удобным и наглядным геометрическим представлением является:

z = a + bi в виде вектора с координатами (а;b) на декартовой плоскости, либо точкой — концом вектора с аналогичными координатами.

В этом случае пару комплексных чисел представляют в виде суммы соответствующих векторов, которую рассчитывают с помощью правила параллелограмма. Согласно теореме Пифагора, длина вектора с координатами (а;b) определяется, как:

Данная величина представляет собой модуль комплексного числа z = a + bi и имеет такое решение:

Вектор и положительное направление оси абсцисс образуют угол, отсчитанный против часовой стрелки. Данный угол называют аргументом комплексного числа z и обозначают, как Arg z. Аргумент имеет неоднозначное определение с точностью до прибавления величины, которая кратна 2π радиан. При повороте на такой угол вокруг начала координат вектор не изменяется.

В том случае, когда вектор длиной r с положительным направлением оси абсцисс составляет угол ϕ, его координаты будут следующими:

\(\left(r*\cos \varphi ;r*\sin \varphi \right)\)

Таким образом, получают тригонометрическую форму записи комплексного числа:

\(z=\left|z \right|*\left(\cos (Arg z)+i\sin (Arg z) \right)\)

Из-за более простого вида вкладок комплексные числа, как правило, представляют в тригонометрической форме.

Существует показательная форма для записи комплексных чисел. Какое-либо комплексное число, не равное нулю, можно представить в показательной форме:

Где \(\left|z \right|\) является модулем комплексного числа,

\(\varphi\) представляет собой аргумент комплексного числа.

Представить комплексное число в показательной форме можно с помощью нескольких действий:

Основные действия над комплексными числами с примерами

Манипуляции с комплексными числами выполняют так же, как с действительными числами. Арифметические действия могут быть следующими:

Складывать и вычитать комплексные числа можно с помощью правила:

(a + bi) ± (c + di) = (a ± c) + (b ± d)i

Умножение комплексных чисел выполняют таким образом:

(a + bi) · (c + di) = (ac – bd) + (ad + bc)i

В данном случае \(i^<2>=-1\)

Число \(\bar=a-bi\) является комплексно-сопряженным к \(z=a+bi\)

С помощью равенства \(z*\bar=a^<2>+b^<2>\) можно установить, как делить одно комплексное число на другое, не равное нулю, комплексное число:

Сложение комплексных чисел

Ели требуется сложить пару комплексных чисел:

Сначала нужно найти сумму их действительных и мнимых частей:

Таким образом, сумма какого-либо количества слагаемых определяется путем сложения действительных частей и сложением мнимых частей. В случае комплексных чисел справедливо правило первого класса, которое гласит, что от перестановки слагаемых их сумма остается прежней:

Вычитание комплексных чисел

Разность комплексных чисел:

Действие аналогично сложению. Разница заключается в необходимости выделения скобками вычитаемого числа. Далее следует раскрыть скобки и изменить знак:

Полученное в результате число обладает двумя частями. Действительная часть является составной:

Наглядно ответ будет записан в такой форме:

Умножение комплексных чисел

Можно найти произведение комплексных чисел:

Произведение будет записано таким образом:

Раскрыть скобки следует, руководствуясь правилом умножения многочленов, учитывая, что \(i^<2>=-1\)

Для того чтобы перемножить многочлены, требуется каждый член одного многочлена умножить на каждый член другого многочлена. Таким образом:

Как и в случае со сложением, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Деление комплексных чисел

На примере комплексных чисел:

требуется определить частное:

Частное будет записано в таком виде:

Делить числа необходимо с помощью метода умножения знаменателя и числителя на сопряженное знаменателю выражение. В этом случае пригодится стандартная формула:

По условию знаменатель 7-6i. В данном знаменателе уже есть (а-b), поэтому сопряженным выражением в таком случае является (a+b), то есть 7+6i. Исходя из правила, знаменатель умножают на 7+6i. Сохранить равенство можно с помощью умножения числителя на то же самое число 7+6i:

Затем в числителе необходимо раскрыть скобки, то есть умножить пару чисел, согласно отмеченному ранее правилу. Для знаменателя требуется использовать формулу \((a-b)(a+b)=a^<2>-b^<2>\) и \(i^<2>=-1\)

Уравнение будет записано в таком виде:

Нахождение аргумента

При выполнении действий с модулем комплексных чисел необходимо руководствоваться формулой:

Для поиска аргумента комплексного числа требуется использовать определенную формулу для конкретного случая. Уравнение подбирается, исходя из положения числа z = a + bi в координатной четверти. Существует всего три таких варианта:

Извлечение корня из комплексных чисел

Комплексные числа в тригонометрической форме умножают таким образом:

z_<1>*z_<2>=\left|z_ <1>\right|*\left|z_ <2>\right|*(\cos (Arg z_<1>+Arg z_<2>)+i\sin (Arg z_<1>+Arg z_<2>))2

При умножении пары комплексных чисел их модули перемножаются, а аргументы складываются. Исходя из этого утверждения, вытекают формулы Муавра:

С помощью этого равенства можно извлечь корни любой степени из комплексных чисел. Корень n-й степени из числа z представляет собой комплексное число w, которое:

Где k может обладать любым значением из множества (0, 1, …, n-1).

Таким образом, в любом случае имеется ровно n корней n-ой степени из комплексного числа. На плоскости все они будут расположены в вершинах правильного n-угольника.

Возведение комплексных чисел в степень

В качестве примера можно возвести в квадрат комплексное число:

Первый способ заключается в записи степени в виде произведения множителей:

Далее необходимо перемножить числа, согласно правилу умножения многочленов.

Второй метод заключается в использовании уравнения для сокращенного умножения:

Выражение примет следующий вид:

В случае комплексного числа можно достаточно просто записать определенную формулу для сокращенного умножения:

Такую же формулу можно представить для расчета квадрата разности, куба суммы и куба разности. Если необходимо возвести в 5-ю, 10-ю или любую другую степень комплексное число, следует воспользоваться тригонометрической формой комплексного числа, то есть формулу Муавра. К примеру, дано комплексное число в тригонометрической форме:

\(x = <-b \pm \sqrt\over 2a>z=\left|z \right|*\left(\cos \varphi +i\sin \varphi \right)\)

Данное число требуется возвести в натуральную степень n. Для этого необходимо использовать уравнение:

\(z^=\left|z \right|^*\left(\cos (n\varphi) +i\sin (n\varphi) \right)\)

Представленная формула вытекает из правила для умножения комплексных чисел, которые записаны в тригонометрической форме. Для того чтобы найти произведение чисел, требуется:

\(z_<1>=\left|z_ <1>\right|*(\cos \varphi _<1>+i\sin \varphi _<1>)\)

\(z_<2>=\left|z_ <2>\right|*(\cos \varphi _<2>+i\sin \varphi _<2>)\)

Далее требуется перемножить модули этих комплексных чисел и найти сумму аргументов:

\(x = <-b \pm \sqrt\over 2a>z_<1>* z_<2>=\left|z_ <1>\right|*\left|z_ <2>\right|*(\cos( \varphi _<1>+\varphi _<2>)+i\sin ( \varphi _<1>+\varphi _<2>)\)

Аналогичный порядок действий для показательной формы комплексного числа:

Источник