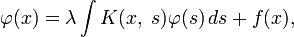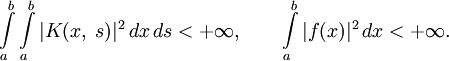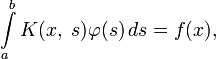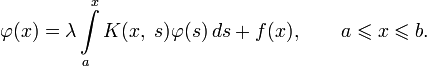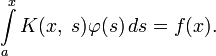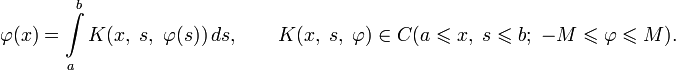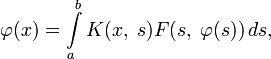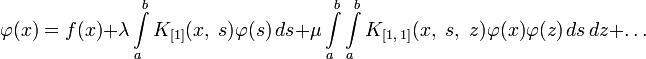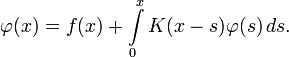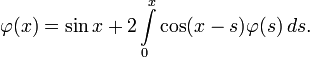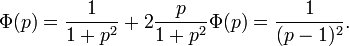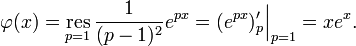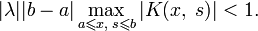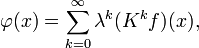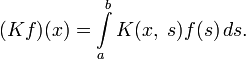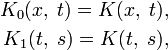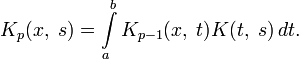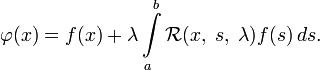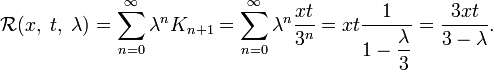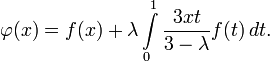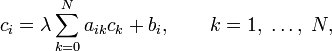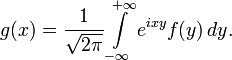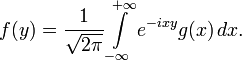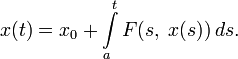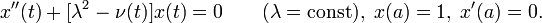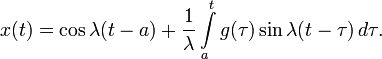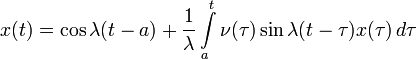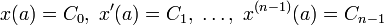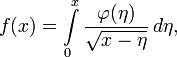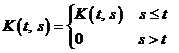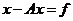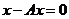Как решать интегральные уравнения
Интегральные уравнения
Интегра́льное уравне́ние — функциональное уравнение, содержащее интегральное преобразование над неизвестной функцией. Если интегральное уравнение содержит также производные от неизвестной функции, то говорят об интегро-дифференциальном уравнении.
Содержание
Классификация интегральных уравнений
Линейные интегральные уравнения
Это интегральные уравнения, в которые неизвестная функция входит линейно:
Уравнения Фредгольма
Уравнения Фредгольма 2-го рода
Уравнения Фредгольма 2-го рода — это уравнения вида:
Пределы интегрирования могут быть как конечными, так и бесконечными. Переменные удовлетворяют неравенству: 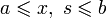

Ядра, удовлетворяющие последнему условию, называют фредгольмовыми. Если 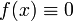
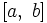
Уравнения Фредгольма 1-го рода
Уравнения Фредгольма 1-го рода выглядят также, как и уравнение Фредгольма 2-го рода, только в них отсутствует часть, содержащая неизвестную функцию вне интеграла:
при этом ядро и свободный член удовлетворяют условиям, сформулированным для уравнений Фредгольма 1-го рода.
Уравнения Вольтерра
Уравнения Вольтерра 2-го рода
Уравнения Вольтера отличаются от уравнений Фредгольма тем, что один из пределов интегрирования в них является переменным:
Уравнения Вольтерра 1-го рода
Также, как и для уравнений Фредгольма, в уравнениях Вольтерра 1-го рода отсутствует неизвестная функция вне интеграла:
В принципе, уравнения Вольтерра можно рассматривать как частный случай уравнений Фредгольма, если переопределить ядро:
Однако некоторые свойства уравнений Вольтерра не могут быть применены к уравнениям Фредгольма.
Нелинейные уравнения
Можно придумать немыслимое многообразие нелинейных уравнений, поэтому дать им полную классификацию не представляется возможным. Вот лишь их некоторые типы, имеющие большое теоретическое и прикладное значение.
Уравнения Урысона
Постоянная M — это некоторое положительное число, которое заранее не всегда может быть определено.
Уравнения Гаммерштейна
Уравнения Гаммерштейна являются важным частным случаем уравнения Урысона:
где 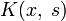
Уравнения Ляпунова — Лихтенштейна
Именами Ляпунова — Лихтенштейна принято называть уравнения, содержащие существенно нелинейные операторы, например, уравнение вида:
Нелинейное уравнение Вольтерра
где функция 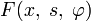
Методы решения
Прежде, чем рассмотреть некоторые методы решения интегральных уравнений, следует заметить, что для них, как и для дифференциальных уравнений не всегда удается получить точное аналитическое решение. Выбор метода решения зависит от вида уравнения. Здесь будут рассмотрены несколько методов для решения линейных интегральных уравнений.
Преобразование Лапласа
Метод преобразования Лапласа может быть применён к интегральному уравнению, если входящий в него интеграл имеет вид свёртки двух функций:
то есть, когда ядро является функцией разности двух переменных:
Например, дано такое уравнение:
Применим преобразование Лапласа к обеим частям уравнения:
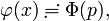
Применяя обратное преобразование Лапласа, получим:
Метод последовательных приближений
Метод последовательных приближений применяется для уравнений Фредгольма 2-го рода, если выполняется условие:
Это условие необходимо для сходимости ряда Лиувилля — Неймана:
Метод резольвент
Метод резольвент является не самым быстрым решением интегрального уравнения Фредгольма второго рода, однако иногда нельзя указать других путей решения задачи.
Если ввести следующие обозначения:
то повторными ядрами ядра 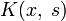
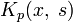
Ряд, составленный из повторных ядер,
называется резольвентой ядра 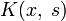
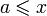
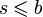
Например, для интегрального уравнения
повторными будут следующие ядра:
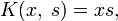
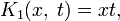
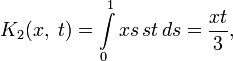
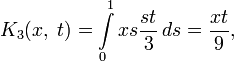
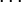
а резольвентой — функция
Тогда решение уравнения находится по формуле:
Метод сведения к алгебраическому уравнению
В случае, если ядро интегрального уравнения Фредгольма является вырожденным, то есть 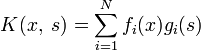
где 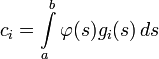
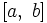
где 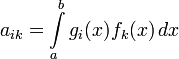
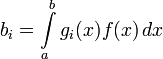
Приложения
Термин «интегральное уравнение» ввёл в 1888 году Дюбуа-Реймон, однако первые задачи с интегральными уравнениями решались и ранее. Например, в 1811 году Фурье решил задачу об обращении интеграла, которая теперь носит его имя.
Формула обращения Фурье
Задача состоит в нахождении неизвестной функции f(y) по известной функции g(x) :
Фурье получил выражение для функции f(y) :
Сведение задачи Коши к интегральному уравнению
К нелинейным интегральным уравнениям Вольтерра приводит задача Коши для обыкновенных дифференциальных уравнений:
В самом деле, это уравнение можно проинтегрировать по t от a до t :
Решение начальной задачи для линейных дифференциальных уравнений приводит к линейным интегральным уравнениям Вольтерра 2-го рода. Этим еще в 1837 году воспользовался Лиувилль. Пусть, например, поставлена задача:
Для уравнения с постоянными коэффициентами с теми же начальными условиями:
решение может быть найдено методом вариации постоянных и представлено в виде:
Тогда для исходного уравнения получается:
— интегральное уравнение Вольтерра 2-го рода.
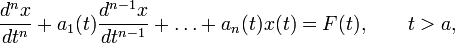
также может быть сведено к интегральному уравнению Вольтерра 2-го рода.
Задача Абеля
Исторически считается, что первой задачей, которая привела к необходимости рассмотрения интегральных уравнений, является задача Абеля. В 1823 году Абель, занимаясь обобщением задачи о таутохроне, пришёл к уравнению:
где f(x) — заданная функция, а 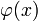
У Абеля формулировка задачи выглядела примерно так:
Если обозначить угол между касательной к траектории и осью Oξ как β и применить законы Ньютона, можно прийти к следующему уравнению:
См. также
Литература
Полезное
Смотреть что такое «Интегральные уравнения» в других словарях:
Интегральные уравнения — уравнения, содержащие неизвестные функции под знаком интеграла. Многочисленные задачи физики и математической физики приводят к И. у. различных типов. Пусть, например, требуется с помощью некоторого оптического прибора получить… … Большая советская энциклопедия
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ — ур ния, содержащие неизвестные ф ции под знаком интеграла. К И. у. приводятся мн. задачи естествознания и техники, например задача о колебаниях, задача о рассеянии лучистой энергии и т. д … Большой энциклопедический политехнический словарь
Сингулярные интегральные уравнения — Интегральные уравнения с ядрами, обращающимися в бесконечность в области интегрирования так, что соответствующий несобственный интеграл, содержащий неизвестную функцию, расходится и заменяется своим главным значением по Коши. Примером С.… … Большая советская энциклопедия
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ — дифференциальные уравнения с частными производными, интегральные уравнения, к которым приводит математический анализ физических явлений. См., напр., Волновое уравнение, Лапласа уравнение, Теплопроводности уравнение … Большой Энциклопедический словарь
уравнения фаддеева — Интегральные уравнения движения квантовомеханической системы трех взаимодействующих частиц … Политехнический терминологический толковый словарь
Уравнения математической физики — дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро дифференциальные и т.д.), к которым приводит математический анализ физических явлений. Для теории У. м. ф.… … Большая советская энциклопедия
уравнения математической физики — дифференциальные уравнения с частными производными, интегральные уравнения, к которым приводит математический анализ физических явлений. См., например, Волновое уравнение, уравнение Лапласа, уравнение теплопроводности. * * * УРАВНЕНИЯ… … Энциклопедический словарь
УРАВНЕНИЯ — Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений. Если равенство справедливо для любых допустимых значений входящих в него неизвестных, то оно называется тождеством; например, соотношение вида… … Энциклопедия Кольера
Интегральные преобразования — Одним из наиболее мощных средств решения дифференциальных уравнений, как обыкновенных, так, особенно, в частных производных, является метод интегральных преобразований. Преобразования Фурье, Лапласа, Ганкеля и другие применяются для решения задач … Википедия
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ — дифференциальные ур ния с частными производными, интегральные ур ния, к к рым приводит матем. анализ физ. явлений. См., напр., Волновое уравнение, Лапласа уравнение, Теплопроводности уравнение … Естествознание. Энциклопедический словарь
СОДЕРЖАНИЕ
Обзор
Численное решение
Стоит отметить, что интегральные уравнения часто не имеют аналитического решения и должны решаться численно. Примером этого является оценка интегрального уравнения электрического поля (EFIE) или интегрального уравнения магнитного поля (MFIE) над объектом произвольной формы в задаче электромагнитного рассеяния.
Один из методов численного решения требует дискретизации переменных и замены интеграла квадратурным правилом.
Тогда у нас есть система с n уравнениями и n переменными. Решая его, мы получаем значение n переменных
Классификация
Интегральные уравнения классифицируются по трем разным дихотомиям, составляющим восемь различных видов:
Как уравнения Фредгольма, так и уравнения Вольтерра являются линейными интегральными уравнениями из-за линейного поведения φ ( x ) под действием интеграла. Нелинейное интегральное уравнение Вольтерра имеет общий вид:
Интегральные уравнения Винера – Хопфа.
Решение степенного ряда для интегральных уравнений
в виде степенного ряда
Интегральные уравнения как обобщение уравнений на собственные значения
В общем случае интегральные уравнения Вольтерра и Фредгольма могут возникать из одного дифференциального уравнения, в зависимости от того, какие условия применяются на границе области его решения.
Тема 4. Интегральные уравнения
§ 1. Типы интегральных уравнений
Линейные интегральные уравнения
Def Интегральное уравнение называется линейным, если в него неизвестная функция входит линейно.


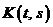

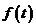


Если уравнение дано, то функции 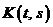
1.2. Уравнения Фредгольма
Различают интегральные уравнения Фредгольма I и II рода.
Def Интегральное уравнения Фредгольма II рода имеет вид

Def Интегральное уравнения Фредгольма I рода имеет вид
(т.е. неизвестная функция вне интеграла отсутствует)
В уравнениях Фредгольма либо 



Если 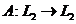
Ядра, удовлетворяющие 
Интегральные уравнения различают однородные и неоднородные.
Def Интегральное уравнение называется однородным, если отсутствует свободный член 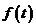



В противном случае уравнение называется неоднородным.
1.3. Уравнения Вольтерра.
Различают уравнения Вольтерра I и II рода.
Def Уравнения Вольтерра II рода имеет вид


Def Уравнения Вольтерра I рода имеет вид


Аналогично уравнениям Фредгольма, среди уравнений Вольтерра различают однородные и неоднородные.
1.4. Связь уравнений Вольтерра с уравнениями Фредгольма.
Уравнение Вольтерра можно рассматривать как частный случай уравнения Фредгольма.
Ядро 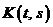
определено при 



Т.е. имеем уравнение Фредгольма с ядром
§ 2. Интегральный оператор Фредгольма.
2.1. Интегральный оператор в 
Def Интегральным определением Фредгольма называется оператор вида

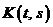
Теорема 1. Пусть 



Теорема 2. Оператор 

1)
2) 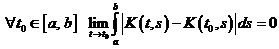
2.2. Интегральный оператор в
Интегральный оператор Фредгольма можно рассматривать и как действующий в 
Но тогда для компактности оператора, естественно, будут другие ограничения.
Теорема 1. Оператор 



Оценка для нормы в этом пространстве выглядит так

Теорема 2. Пусть дан оператор 


В частности, оператор 


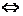

§ 3. Альтернатива Фредгольма.
3.1. Операторные уравнения.
Заметим, что теоремы Фредгольма справедливы не только для интегральных уравнений, но и для более общих операторных уравнений с компактными операторами.
Поэтому выпишем как интегральные, так и операторные уравнения, участвующие в теоремах.
Интегральное уравнение Фредгольма II рода неоднородное
(1)
Интегральное уравнение Фредгольма II рода однородное
(2)
Интегральное уравнение Фредгольма II рода неоднородное, сопряженное
(3)
Интегральное уравнение Фредгольма II рода однородное, сопряженное
(4) 
Уравнение II рода неоднородное
( 
Уравнение II рода однородное
( 
И, аналогично, сопряженные уравнения
( 
( 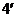

3.2. Теоремы Фредгольма.
Теорема 1 (Первая теорема Фредгольма)
Пусть 
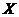
а) уравнение ( 
б) уравнение ( 
в) уравнение ( 
г) уравнение ( 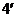
Замечание 1. Утверждение об эквивалентности условий а) и б) называют альтернативой Фредгольма: либо уравнение ( 


Замечание 2. Если выполнено одно из условий а) –г) то операторы 


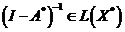
Теорема 2 (II теорема Фредгольма)
Пусть 
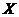

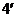
Теорема 3 (III теорема Фредгольма)
Пусть 
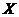




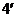

Объединяя результаты теорем, можно сделать следующий вывод:
1) Либо уравнения ( 


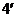
2) Либо однородные уравнения ( 
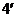
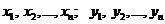




Общие решения ( 


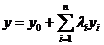
где 
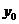




3.3. Приложения к спектру компактного оператора.
В теоремах Фредгольма по существу речь идет об обратимости оператора 




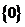

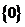
§ 4. Уравнение с вырожденным ядром
4.1. Определение вырожденного ядра.
Def Ядро 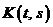
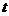
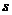

4.2. Схема решения уравнения.
Рассмотрим интегральное уравнение Фредгольма II рода с вырожденным ядром 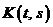


Заметим, что этот оператор конечномерен, т.к. образ действия оператора является линейной комбинацией конечного числа функций.
Очевидно, что решение интегрального уравнения с вырожденным ядром сводится к определению постоянных 

Если система не имеет решения, то, очевидно, интегральное уравнение также не имеет решения.
§ 5. Уравнения с симметричным ядром.
5.1. Характеристические числа интегрального уравнения.
Однородное интегральное уравнение Фредгольма II рода
(1)
всегда имеет нулевое (тривиальное) решение 
Те значения 


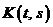

В случае произвольного ядра характеристические числа являются нулями определителя Фредгольма 

Уравнение Вольтерра разрешимо 
Если же ядро симметрично, то оператор имеет, по крайней мере, одно характеристическое число.
5.2. Общий вид решения интегрального уравнения с симметричным ядром.
Теорема 1. Если 







В 



Теорема 2. Если функция 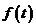


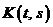

Теорема 3. Пусть 



Тогда решение уравнения (1) существует 


При этом (1) имеет 



Вывод. Очевидно, чтобы найти решение уравнения (1) достаточно знать характеристические числа и собственные функции оператора 
5.3. Схема нахождения характеристических чисел и собственных функций.
На практике обычно сталкиваются со случаем, когда интегральное уравнение с симметрическим ядром является решением некоторой самосопряженной однородной краевой задачи для обыкновенного дифференциального уравнения.
В таких случаях нахождение характеристических чисел и собственных функций ядра (оператора) сводится к решению указанной краевой задачи.
Т.е. мы должны дважды продифференцировав наше интегральное уравнение составить некоторое дифференциальное уравнение, и найдя краевые значения 



Решается дифференциальное уравнение стандартно, используя общие решения.
§ 6. Уравнения типа свертки.
6.1 Уравнения Вольтерра.
Def Уравнением Вольтерра второго рода называется интегральное уравнение

где 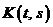

Поскольку это уравнение можно рассматривать как частный случай уравнения Фредгольма (с ядром, равным нулю при 
Однако для уравнений Вольтерра эти теоремы можно уточнить следующим образом.
Уравнение Вольтерра, при любой функции 
6.2. Уравнение типа свертки.
Def Уравнением типа свертки называется интегральное уравнение Вольтерра II рода, ядро которого зависит лишь от разности аргументов
При этом функции 
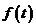

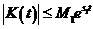
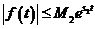
Решение уравнения типа свертки можно отыскать с помощью преобразования Лапласа.
§ 7. Преобразование Лапласа.
7.1. Определение функции-оригинала и изображения функции.
Def Функцией-оригиналом называется любая комплекснозначная функция 
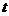
1) 
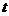
2) для всех отрицательных
3) 
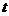

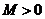
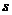

Мы будем рассматривать непрерывные функции-оригинала.
Def Изображением функции 



То, что 

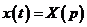
Функция 


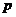
7.2. Свойства преобразования Лапласа.
1. Свойство линейности.
Для любых комплексных постоянных 

Для любого постоянного 
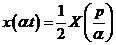
3. Дифференцирование оригинала.
Если функции 


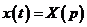






4. Дифференцирование изображения.
Дифференцирование изображения сводится к умножению на 


5. Интегрирование оригинала.
Интегрирование оригинала сводится к делению изображения на 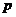
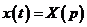

6. Интегрирование изображения
Если 

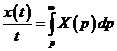
7. Теорема смещения
Если 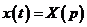


8. Теорема запаздывания. Если 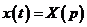

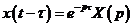
9. Теорема умножения (теорема о свертке).
Произведение двух изображений 


Интеграл в правой части называется сверткой функций 
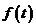

7.3. Таблица преобразования Лапласа.
Так как времени осваивать свойства преобразования у нас нет, то основные результаты вынесем в таблицу.
 |  |  |  |  |  |
 |  |  |  | 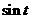 |  |
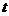 | 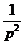 |  |  |  |  |
 | 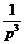 |  |  | 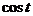 |  |
 |  | 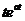 |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
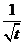 |  |  |  |  |  |
§ 8. Решение уравнений типа свертки.
Пусть имеем интегральное уравнение Вольтерра II рода типа свертки

Предположим, что функции 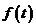

Можно показать, что в этом случае решение 
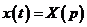







Заметим, что если 
Дата добавления: 2018-04-05 ; просмотров: 582 ; Мы поможем в написании вашей работы!