Как решать графическим методом

Как решать графическим методом

Объединяем уравнения в систему с помощью фигурной скобки:

Графический метод

Недаром ответ записывается так же, как координаты какой-нибудь точки.

Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.

Например, построим графики уравнений из предыдущего примера.

Пример 1

Для этого сперва выразим y y y в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно x x x ):

Для того чтобы графически решить систему уравнений с двумя переменными нужно:

1) построить графики уравнений в одной системе координат;
2) найти координаты точек пересечения этих графиков (координаты точек пересечения графиков и есть решения системы);

Разберем это задание на примере.

Решить графически систему линейных уравнений.

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Пример 2

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может:

а) иметь единственное решение;

б) не иметь решений;

в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Пример 3

Графическое решение системы

Пример 4

Решить графическим способом систему уравнений.

Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.

Прямую y=x+1 провели через точки (0; 1) и (2; 3).

Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.

Пример 5

Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.

Наши прямые пересеклись в точке В(-2; 5).

ОБЯЗАТЕЛЬНО: Познакомимся с видео, где нам объяснят как решаются системы линейных уравнений графическим способом. РАССКАЖУТ, КАК РЕШАТЬ СИСТЕМЫ ГРАФИЧЕСКИ.

Видео YouTube

Источник

Решение задач линейного программирования графическим методом

Описание метода

Если в задаче линейного программирования имеется только две переменные, то ее можно решить графическим методом.

Построение области допустимых решений

Графический метод решения задачи (1) следующий.
Вначале мы проводим оси координат и и выбираем масштаб. Каждое из неравенств системы ограничений (1.2) определяет полуплоскость, ограниченную соответствующей прямой.

Тоже самое выполняем для остальных неравенств системы (1.2). Так мы получим заштрихованных полуплоскостей. Точки области допустимых решений удовлетворяют всем неравенствам (1.2). Поэтому, графически, область допустимых решений (ОДР) является пересечением всех построенных полуплоскостей. Заштриховываем ОДР. Она представляет собой выпуклый многоугольник, грани которого принадлежат построенным прямым. Также ОДР может быть неограниченной выпуклой фигурой, отрезком, лучом или прямой.

Может возникнуть и такой случай, что полуплоскости не содержат общих точек. Тогда областью допустимых решений является пустое множество. Такая задача решений не имеет.

Можно упростить метод. Можно не заштриховывать каждую полуплоскость, а вначале построить все прямые
(2)
Далее выбрать произвольную точку, не принадлежащую ни одной из этих прямых. Подставить координаты этой точки в систему неравенств (1.2). Если все неравенства выполняются, то область допустимых решений ограничена построенными прямыми и включает в себя выбранную точку. Заштриховываем область допустимых решений по границам прямых так, чтобы оно включало в себя выбранную точку.

Если хотя бы одно неравенство не выполняется, то выбираем другую точку. И так далее, пока не будет найдены одна точка, координаты которой удовлетворяют системе (1.2).

Нахождение экстремума целевой функции

Итак, мы имеем заштрихованную область допустимых решений (ОДР). Она ограничена ломаной, состоящей из отрезков и лучей, принадлежащих построенным прямым (2). ОДР всегда является выпуклым множеством. Оно может быть как ограниченным множеством, так и не ограниченным вдоль некоторых направлений.

Рассмотрим случай, когда крайняя прямая, параллельная произвольной прямой вида (3), проходит через одну вершину многоугольника ОДР. Из графика определяем координаты этой вершины. Тогда максимальное (минимальное) значение целевой функции определяется по формуле:
.
Решением задачи является
.

Пример решения задачи линейного программирования графическим методом

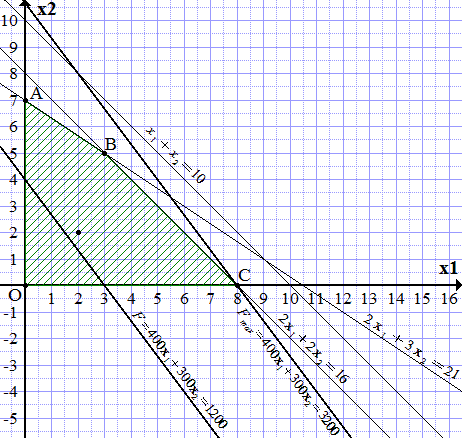
Составить план производства, обеспечивающий фирме наибольший доход. Задачу решить графическим методом.

Тогда экономико-математическая модель задачи имеет вид:

Прямые и являются осями координат.

Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

Заштриховываем область, чтобы точка (2; 2) попала в заштрихованную часть. Получаем четырехугольник OABC.

.
То есть, для получения наибольшего дохода, необходимо изготовить 8 платьев модели А. Доход при этом составит 3200 ден. ед.

Пример 2

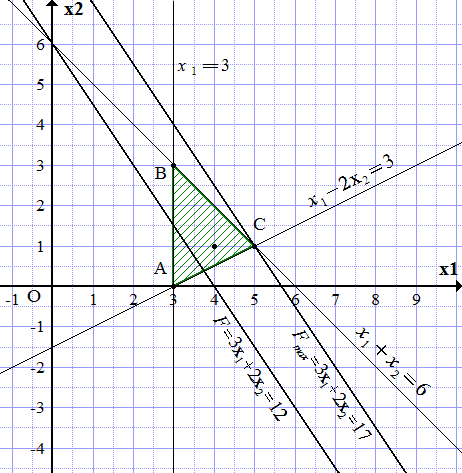
Решить задачу линейного программирования графическим методом.

Область допустимых решений (ОДР) ограничена построенными прямыми. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

Заштриховываем область по границам построенных прямых, чтобы точка (4; 1) попала в заштрихованную часть. Получаем треугольник ABC.

Пример отсутствия решения

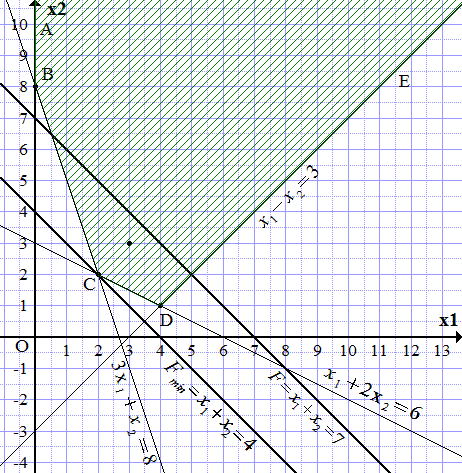
Решить графически задачу линейного программирования. Найти максимальное и минимальное значение целевой функции.

Прямые и являются осями координат.

Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

Заштриховываем область, чтобы точка (3; 3) попала в заштрихованную часть. Получаем неограниченную область, ограниченную ломаной ABCDE.

Максимального значения не существует.
Минимальное значение
.

Источник

Решение систем уравнений

Содержание:

Графический метод решения систем уравнений

Вспоминаем то, что знаем

Что такое график уравнения с двумя неизвестными?

Что представляет собой график линейного уравнения с двумя неизвестными?

Решите графическим методом систему линейных уравнений:

Открываем новые знания

Решите графическим методом систему уравнений:

Как можно решить систему двух уравнений с двумя неизвестными с помощью графиков уравнений этой системы? Отвечаем, проверяем себя по тексту

В курсе алгебры 7-го класса вы изучали системы линейных уравнений.

Для их решения вы применяли три метода: графический, метод подстановки и метод алгебраического сложения. Эти же методы служат и для решения других систем двух уравнений с двумя неизвестными, в которых могут содержаться уравнения второй степени или другие рациональные уравнения — как целые, так и дробные.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Начнём с графического метода

Этот метод основан на том, что каждому уравнению с двумя неизвестными соответствует некоторое множество точек координатной плоскости (график этого уравнения). Построив графики уравнений, мы найдём точки пересечения этих графиков (если они есть), и пары чисел — координаты точек пересечения — будут представлять собой решения системы уравнений.

Найденные решения будут, вообще говоря, приближёнными, в зависимости от точности построений соответствующих графиков.

Таким образом, решить графически систему уравнений — значит найти общие точки графиков уравнений, входящих в систему.

Возможно вам будут полезны данные страницы:

Примеры с решением

Пример 1:

Решим систему уравнений:

Построим графики уравнений

Графиком первого уравнения является парабола, с вершиной в точке (0; 1) и ветвями, направленными вверх, графиком второго — прямая, проходящая через точки (0; 3) и (-3; 0).

Парабола и прямая пересекаются в точках А(2; 5) и В(— 1; 2).

Проверкой убеждаемся, что найденные пары чисел действительно являются решениями системы.

Пример 2:

Выясним количество решений системы уравнений:

Построим графики уравнений

Графики этих уравнений — окружности. Центр первой окружности — начало координат, а её радиус равен 2; центр второй окружности — точка Р(1; — 1), её радиус равен 3.

Окружности пересекаются в двух точках М и N, координаты которых можно найти приближённо. Поскольку нам нужно определить только количество решений, мы делать этого не будем.

Решение систем уравнений методом подстановки

Вспоминаем то, что знаем

Расскажите, как решить систему двух линейных уравнений с двумя неизвестными методом подстановки.

Решите систему линейных уравнений методом подстановки:

Открываем новые знания

Как вы думаете, можно ли применять метод подстановки при решении систем, где не все уравнения являются линейными? При каком условии это удастся сделать?

Решите систему уравнений методом подстановки:

Как решить систему двух уравнений с двумя неизвестными методом подстановки?

Всякую ли систему двух уравнений с двумя неизвестными можно решить методом подстановки?

Ранее вы решали системы уравнений первой степени.

Теперь познакомимся с системами, в которых хотя бы одно уравнение не является линейным. Как и прежде, распространённым методом решения систем является метод подстановки.

Пример 3:

Пусть (х; у) — решение системы.

Выразим х из уравнения

Подставим найденное выражение в первое уравнение:

Решим полученное уравнение:

Убедиться, что найденные пары чисел действительно являются решениями системы, можно подстановкой.

Чуть сложнее дело обстоит в следующем примере.

Пример 4:

Решим систему уравнений:

Пусть (х; у) — решение системы.

Выразим у из линейного уравнения:

Подставим найденное выражение в первое уравнение системы:

После преобразований получим:

Если это целесообразно, то можно осуществлять подстановку некоторого выражения «в целом».

Пример 5:

Подставим во второе уравнение тогда его можно переписать в виде:

Теперь выразим х через у из первого уравнения системы:

Подставим в полученное ранее уравнение ху = 2:

Корни этого уравнения:

.

Иногда решить систему можно, используя метод алгебраического сложения.

Пример 6:

Сложим уравнения, предварительно умножив первое уравнение на —1. В результате получим:

.

Корни этого уравнения:

Подставим найденные значения в первое уравнение. Рассмотрим два случая:

1)

2) , получим уравнение корней нет.

Иногда упростить решение удаётся, используя различные варианты замены неизвестных.

Пример 7:

Решим систему уравнений:

Обозначим

Второе уравнение системы примет вид:

Решим полученное уравнение. Получим, умножая обе части на 2а:

Осталось решить методом подстановки линейные системы:

Ответ: (2; 1), (1; 2). Решение задач с помощью систем уравнений Знакомимся с новыми знаниями

Напомним, что при решении задач обычно действуют следующим образом:

1) обозначают буквами какие-нибудь неизвестные величины, выражают через них другие величины, составляют систему уравнений;

2) решают полученную систему;

3) отвечают на вопрос задачи.

Пример 8:

Периметр прямоугольника равен 34 см, а его диагональ 13 см. Найдите стороны прямоугольника.

Пусть х см — длина, у см — ширина (х у), тогда периметр прямоугольника — см.

Воспользуемся теоремой Пифагора:

Решим систему. Выразим из первого уравнения у:

Подставим во второе уравнение:

Корни уравнения:

Найдём

С учётом условия получим ответ: длина — 12 см, ширина — 5 см.

Пример 9:

Если произведение двух положительных чисел увеличить на первое из них, то получится 128. Если это же произведение увеличить на второе из них то получится 135. Найдите эти числа.

Пусть х — первое число, у — второе число.

Тогда: — произведение, увеличенное на первое число, ху 4-у — произведение, увеличенное на второе число.

Вычтем из второго уравнения первое. Получим:

Дальше будем решать методом подстановки:

Подставим в первое уравнение выражение для у:

Корни уравнения: (не подходит по смыслу задачи).

Найдём у из уравнения:

Получим ответ: 16 и 7.

Симметричные системы уравнений с двумя неизвестными

Уравнение с двумя неизвестными называется симметричным, если при перестановке этих неизвестных местами уравнение не меняется. Например, уравнение симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид , то есть не меняется. А вот уравнение не симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид , то есть меняется.

Система двух уравнений с двумя неизвестными называется симметричной, если каждое уравнение этой системы симметричное.

ПРЕДУПРЕЖДЕНИЕ. В определении симметричной системы уравнений требуется, чтобы каждое уравнение в отдельности не менялось.

Например, если в системе уравнений

переставить местами неизвестные х и у, то получим систему:

Видно, что система в целом не изменилась (уравнения поменялись местами по сравнению с первоначальной системой). Но такая система не является симметричной, так как каждое из уравнений в отдельности изменилось.

Убедитесь, что симметричные системы с двумя неизвестными х и у можно решать с помощью замены неизвестных:

Сначала научитесь выражать через неизвестные выражения:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Решение уравнений и неравенств (с помощью графиков)

Многие задания, которые мы привыкли вычислять чисто алгебраически, можно решить намного легче и быстрее!

С помощью графиков функций!

Ты скажешь: «Как так? Чертить что-то, да и что чертить?» Поверь мне, иногда это удобнее и проще.

Приступим? Начнем с решения уравнений!

Решение уравнений и неравенств с помощью графиков — коротко о главном

Более подробно о построении графиков функций смотри в теме «Функции».

Решение уравнений с помощью графиков

Решение линейных уравнений

Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида.

Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень.

Сейчас же я покажу тебе, как это сделать графическим способом.

Итак, у тебя есть уравнение: \( \displaystyle 2 -10=2\)

Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:

Обычно дальше мы делим правую часть на левую, и получаем искомый корень, но мы с тобой попробуем построить левую и правую части как две различные функции в одной системе координат.

Иными словами, у нас будет:

А теперь строим. Что у тебя получилось?

Как ты думаешь, что является корнем нашего уравнения? Правильно, координата \( \displaystyle x\) точки пересечения графиков:

Наш ответ: \( \displaystyle x=6\)

Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число \( \displaystyle 6\)!

Вариант 2

Как я говорила выше, это самый распространенный вариант, приближенный к алгебраическому решению, но можно решать и по-другому. Для рассмотрения альтернативного решения вернемся к нашему уравнению:

\( \displaystyle 2 -10=2\)

В этот раз не будем ничего переносить из стороны в сторону, а построим графики напрямую, так, как они сейчас есть:

Что является решением на этот раз? Все верно. То же самое: координата \( \displaystyle x\) точки пересечения графиков:

И снова наш ответ: \( \displaystyle x=6\).

Как ты видишь, с линейными уравнениями все предельно просто. Настало время рассмотреть что-нибудь посложнее… Например, графическое решение квадратных уравнений.

Решение квадратных уравнений

Итак, теперь приступим к решению квадратного уравнения. Допустим, тебе нужно найти корни у этого уравнения:

Конечно, ты можешь сейчас начать считать через дискриминант, либо по теореме Виета, но многие на нервах ошибаются при умножении или возведении в квадрат, особенно, если пример с большими числами, а калькулятора, как ты знаешь, у тебя на экзамене не будет…

Поэтому давай попробуем немного расслабиться и порисовать, решая данное уравнение.

Графически найти решения данного уравнения можно различными способами. Рассмотрим различные варианты, а уже ты сам выберешь, какой больше всего тебе понравится.

Вариант 1. Напрямую

Просто строим параболу по данному уравнению: \( \displaystyle <^<2>>+2 -8=0\)

Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:

Ты скажешь «Стоп! Формула для \( \displaystyle y\) очень похожа на формулу нахождения дискриминанта» да, так оно и есть, и это является огромным минусом «прямого» построения параболы, чтобы найти ее корни.

Тем не менее, давай досчитаем до конца, а потом я покажу, как это сделать намного (намного!) проще!

Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:

Точно такой же ответ? Молодец!

И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, \( \displaystyle 3\).

Ты знаешь, что парабола симметрична относительно своей вершины, например:

Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:

Возвращаемся к нашей параболе.

Мне удобней работать с положительными, поэтому я рассчитаю при \( \displaystyle x=0\) и \( \displaystyle x=2\).

При \( \displaystyle x=0\):

При \( \displaystyle x=2\):

Теперь у нас есть три точки, и мы спокойно можем построить нашу параболу, отразив две последние точки относительно ее вершины:

Как ты думаешь, что является решением уравнения?

Правильно, точки, в которых \( \displaystyle y=0\), то есть \( \displaystyle x=2\) и \( \displaystyle x=-4\). Потому что \( \displaystyle <^<2>>+2 -8=0\).

И если мы говорим, что \( \displaystyle y=<^<2>>+2 -8\), то значит, что \( \displaystyle y\) тоже должен быть равен \( \displaystyle 0\), или \( \displaystyle y=<^<2>>+2 -8=0\).

Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!

Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант.

Что у тебя получилось? То же самое?

Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!

Вариант 2. С разбивкой на несколько функций

Возьмем все тоже наше уравнение: \( \displaystyle <^<2>>+2 -8=0\), но запишем его несколько по-другому, а именно:

Можем мы так записать? Можем, так как преобразование равносильно. Смотрим дальше.

Построим отдельно две функции:

Построил? Сравним с тем, что вышло у меня:

Как ты считаешь, что в данном случае является корнями уравнения? Правильно! Координаты по \( \displaystyle x\), которые получились при пересечении двух графиков: \( \displaystyle <_<1>>=<^<2>>\) и \( \displaystyle <_<2>>=8-2x\), то есть:

Соответственно, решением данного уравнения являются:

Что скажешь? Согласись, этот способ решения намного легче, чем предыдущий, и даже легче, чем искать корни через дискриминант!

А если так, попробуй данным способом решить следующее уравнение.

Что у тебя получилось? Сравним наши графики:

По графикам видно, что ответами являются:

Теперь посмотрим уравнения чууууть-чуть посложнее, а именно решение смешанных уравнений, то есть уравнений, содержащих функции разного вида.

Решение смешанных уравнений

Теперь попробуем решить следующее уравнение:

Конечно, можно привести все к общему знаменателю, найти корни получившегося уравнения, не забыв при этом учесть ОДЗ, но мы попробуем решить графически, как делали во всех предыдущих случаях.

В этот раз давай построим 2 следующих графика:

Осознал? Теперь займись построением.

Вот что вышло у меня:

Глядя на этот рисунок, скажи, что является корнями нашего уравнения \( \displaystyle \frac<3>-x+2=0\)?

Правильно, \( \displaystyle <_<1>>=-1\) и \( \displaystyle <_<2>>=3\). Вот и подтверждение:

Попробуй подставить наши корни в уравнение. Получилось?

Все верно! Согласись, графически решать подобные уравнения – одно удовольствие!

Попробуй самостоятельно графическим способом решить уравнение:

Даю подсказку: перенеси часть уравнения в правую сторону, чтобы с обоих сторон оказались простейшие для построения функции. Намек понял? Действуй!

Теперь посмотрим, что у тебя вышло:

\( \displaystyle 2<^<3>>=x+1\), соответственно:

Как ты уже давно у себя записал, корнем данного уравнения является \( \displaystyle <_<1>>=1\).

Прорешав такое количество примеров, уверена, ты понял, как можно легко и быстро решать уравнения графическим путем. Настало время разобраться, как решать подобным способом системы.

Решение систем уравнений с помощью графиков

Графическое решение систем, по сути, ничем не отличается от графического решения уравнений.

Мы будем строить два графика, и их точки пересечения будут являться корнями данной системы.

Один график – одно уравнение, второй график – другое уравнение. Все предельно просто!

Начнем с самого простого – решение систем линейных уравнений.

Решение систем линейных уравнений

Допустим, у нас есть следующая система:

Для начала преобразуем ее таким образом, чтобы слева было все, что связано с \( \displaystyle y\), а справа – что связано с \( \displaystyle x\). Иными словами, запишем данные уравнения как функцию в привычном для нас виде:

А теперь просто строим две прямые. Что в нашем случае является решением? Правильно! Точка их пересечения! И здесь необходимо быть очень-очень внимательным! Подумай, почему?

Намекну: мы имеем дело с системой, в системе есть и \( \displaystyle x\), и \( \displaystyle y\)… Смекаешь?

Все верно! Решая систему, мы должны смотреть обе координаты, а не только \( \displaystyle x\), как при решении уравнений!

Записал? Теперь давай все сравним по порядку:

И ответы: \( \displaystyle x=1\) и \( \displaystyle y=-1\). Сделай проверку – подставь найденные корни в систему и убедись, правильно ли мы ее решили графическим способом?

Все сошлось? Идем дальше!

Решение систем нелинейных уравнений

А что если вместо одной прямой, у нас будет квадратное уравнение? Да ничего страшного! Просто ты вместо прямой построишь параболу! Не веришь? Попробуй решить следующую систему:

Какой наш следующий шаг? Правильно, записать так, чтобы нам было удобно строить графики:

А теперь так вообще дело за малым – построил быстренько и вот тебе решение! Строим:

Графики получились такими же? Теперь отметь на рисунке решения системы и грамотно запиши выявленные ответы!

Все сделал? Сравни с моими записями:

При \( \displaystyle <_<1>>=-1\), \( \displaystyle <_<1>>=0\).

При \( \displaystyle <_<2>>=2\), \( \displaystyle <_<2>>=-3\).

Все верно? Молодец! Ты уже щелкаешь подобные задачи как орешки! А раз так, дадим тебе систему посложнее.

Решите систему уравнений: \( \displaystyle \left\< \beginy=<^<2>>+2x+2;\\y-<^<3>>=2.\end \right.\)

Что мы делаем? Правильно! Записываем систему так, чтобы было удобно строить:

Немного тебе подскажу, так как система выглядит ну очень не простой! Строя графики, строй их «побольше», а главное, не удивляйся количеству точек пересечения.

Итак, поехали! Выдохнул? Теперь начинай строить!

Ну как? Красиво? Сколько точек пересечения у тебя получилось? У меня три! Давай сравнивать наши графики:

Так же? Теперь аккуратно запиши все решения нашей системы:

При \( \displaystyle <_<1>>=-1\), \( \displaystyle <_<1>>=1\).

При \( \displaystyle <_<2>>=0\), \( \displaystyle <_<2>>=2\).

При \( \displaystyle <_<3>>=2\), \( \displaystyle <_<3>>=10\).

А теперь еще раз посмотри на систему:

Представляешь, что ты решил это за каких-то 15 минут?

Согласись, математика – это все-таки просто, особенно когда, глядя на выражение, не боишься ошибиться, а берешь и решаешь! Ты большой молодец!

Решение неравенств с помощью графиков

Решение линейных неравенств

После последнего примера тебе все по плечу! Сейчас выдохни – по сравнению с предыдущими разделами этот будет очень-очень легким!

Начнем мы, как обычно, с графического решения линейного неравенства. Например, вот этого:

Неравенство нестрогое, поэтому \( \displaystyle 4\) — не включается в промежуток, и решением будут являться все точки, которые находятся правее \( \displaystyle 4\), так как \( \displaystyle 5\) больше \( \displaystyle 4\), \( \displaystyle 6\) больше \( \displaystyle 4\) и так далее:

Ответ: \( x\in \left( 4;+\infty \right)\)

Вот и все! Легко? Давай решим простое неравенство с двумя переменными:

Решение неравенства с двумя переменными

\( 2 -3

Такой график у тебя получился? А теперь внимательно смотрим, что там у нас в неравенстве? Меньше? Значит, закрашиваем все, что находится левее нашей прямой.

А если было бы больше Правильно, тогда закрашивали бы все, что находится правее нашей прямой. Все просто.

Все решения данного неравенства «затушеваны» синим цветом. Вот и все, неравенство с двумя переменными решено. Это значит, что координаты \( \displaystyle x\) и \( \displaystyle y\) любой точки из закрашенной области и есть решения.

Решение квадратных неравенств

Теперь будем разбираться с тем, как графически решать квадратные неравенства.

Но прежде, чем перейти непосредственно к делу, давай повторим некоторый материал, касающийся квадратной функции \( \displaystyle a<^<2>>+bx+c=0\).

Что показывает нам знак при коэффициенте \( \displaystyle a\)? Верно, куда направлены ветви параболы – вверх или вниз (не помнишь? Почитай теорию «Квадратичная функция»).

А за что у нас отвечает дискриминант? Правильно, за положение графика относительно оси \( \displaystyle Ox\) (если не помнишь этого, то тогда точно прочти теорию о квадратичных функциях).

В любом случае, вот тебе небольшая табличка-напоминалка:

Симметрично отражаем наши точки на другую ветвь параболы:

Так как в нашем неравенстве стоит знак строго меньше, то конечные точки мы исключаем – «выкалываем».

Согласись, это намного быстрее.

Рассмотрим еще один способ решения, который упрощает и алгебраическую часть, но главное не запутаться.

Вариант 3

Ответ: \( \displaystyle \left[ 2;4 \right]\).

Решение смешанных неравенств

Теперь перейдем к более сложным неравенствам!

\( \displaystyle 4x

У тебя так же? Отлично!

Теперь расставим точки пересечения и цветом определим, какой график у нас по идее должен быть больше, то есть \( \displaystyle <_<2>>=<^<3>>\).

Смотри, что получилось в итоге:

А теперь просто смотрим, в каком месте у нас выделенный график находится выше, чем график \( \displaystyle <_<1>>=4x\)? Смело бери карандаш и закрашивай данную область! Она и будет решением нашего сложного неравенства!

Ну вот, теперь тебе по плечу и любое уравнение, и любая система, и уж тем более любое неравенство!

Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике

В следующих вебинарах вы сможете отработать навык решения уравнений, неравенств и систем алгебраическим способом.

Решение линейных уравнений (алгебраически)

Цель урока — научиться решать линейные уравнения любого уровня сложности. Линейные уравнения – основа всей алгебры. Научитесь решать линейные уравнения, и вам будет намного проще осваивать всё остальное.

Приёмы, которые мы узнаем на этом уроке, применяются не только в линейных, но во всех типах уравнений, от квадратных до логарифмических. Все приёмы будем разбирать на конкретных примерах и сразу же отрабатывать.

Мы решим разберём все возможные типы линейных уравнений, решив 65 уравнений.

ЕГЭ №15. Решение уравнений и неравенств методом интервалов

В этом видео мы узнаем (вспомним) метод интервалов, поймём как и почему он работает. Вспомним, как решать квадратные, рациональные неравенства, а также неравенства с модулем и иррациональные.

Источник