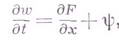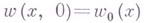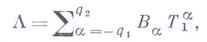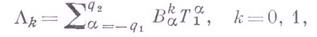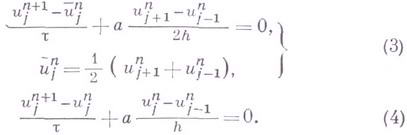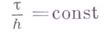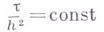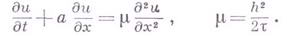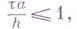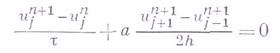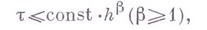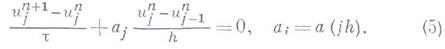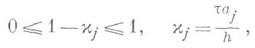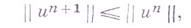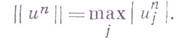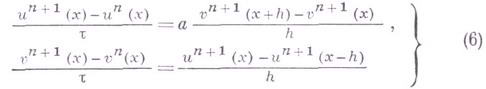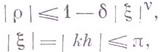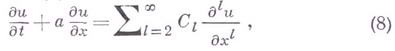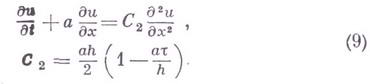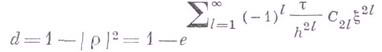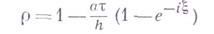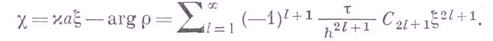Как решать гиперболические уравнения
Как решать гиперболические уравнения
Глава 5. Решение дифференциальных уравнений
5.8 Функции решения параболических и гиперболических уравнений
Дифференциальные уравнения в частных производных требуют нахождение функции не одной, а нескольких переменных. MathCAD имеет очень ограниченные возможности для решения таких уравнений, ведь для решения каждого вида уравнений в частных производных требуется свой метод решения.
Уравнения в частных производных можно разделить на три типа:
1) параболические, содержащие первую производную по одной переменной и вторую – по другой, причем все производные входят в уравнение с одинаковым знаком;
2) гиперболические, содержащие первую производную по одной переменной и вторую – по другой, входящие в уравнение с разными знаками;
3) эллиптические, содержащие вторые производные, причем одного знака.
Функции решения параболических и гиперболических уравнений
Обращение к этой функции:
возвращает скалярную (для одного уравнения) или векторную (для системы уравнений) функцию, являющуюся решением уравнения (или системы уравнений). Здесь u –явно заданный вектор имен функций (без указания имен аргументов), подлежащих вычислению. Эти функции, а также граничные условия должны быть определены внутри вычислительного блока Given – pdesolve ; х – пространственная координата; x range – вектор значений аргумента х для граничных условий. Он должен состоять из двух чисел, представляющих две границы расчетного интервала; t – время (имя второго аргумента неизвестной функции); t range – вектор значений аргумента t для граничных условий, состоящих из двух чисел, представляющих две границы расчетного интервала; x pts – количество пространственных точек дискретизации (может не указываться); t pts – количество временных слоев (может не указываться).
Решение одномерного волнового уравнения
где 
Представим первое уравнение как систему двух
уравнений первого порядка
Given 
граничные условия 




Рис. 5.1 9 Пример использования функции pdesolve
Единичное решение волнового уравнения
Сетка решений волнового уравнения на временном и пространственном интервалах
Рис. 5. 20 Результаты решения волнового уравнения
Обратите внимание на то, что уравнения внутри вычислительного блока должны записываться с аргументами. Для идентификации частных производных следует использовать нижний индекс, например, 
Недостатком функции pdesolve (как и функции Odesolve ) является невозможность ее использования в составе выражения – программы для многократного решения дифференциального уравнения. При необходимости многократного решения обыкновенных дифференциальных уравнений в состав программного модуля можно включать функции Rkadapt или Bulstoer.
Обращение к этой функции:
возвращает матрицу решения дифференциального уравнения 
Вектор граничных условий может иметь значения трех типов:
– rhs содержит вторые пространственные производные: граничные условия (или Дирихле « D », или Неймана « N ») требуются по одному с каждой стороны интервала интегрирования;
– rhs содржит первые пространственные производные: граничные условия Дирихле на левой или правой границе интервала, на другой стороне NA ;
– нет пространственных производных – граничные условия не требуются.
Функциональная матрица bc содержит три столбца, имеющих ледующий вид:
– ( init _ left ( t ) init _ right ( t ) » D «) – для граничных условий Дирихле;
– ( init _ left ( t ) init _ right ( t ) » N «) – для граничных условий Неймана.

ГИПЕРБОЛИЧЕСКОГО ТИПА УРАВНЕНИЕ
Различные математич. модели во многих случаях приводят к дифференциальным уравнениям гиперболич. типа. Такие уравнения имеют точные аиалитич. решения только в редких случаях. Наиболее распространенными являются численные методы. Они находят широкое применение при решениях задач механики сплошной среды и, в частности, уравнений газовой динамики (см. Газовой динамики численные методы), к-рые по своей структуре являются квазилинейными.
Численные методы решения уравнений гиперболического типа можно разделить на две группы: 1) методы с явным выделением особенностей решения; 2) методы сквозного счета, в к-рых особенности решения явно не выделяются, а получаются в процессе счета как области с резким изменением решений.
К первой группе относится, напр., метод характеристик, к-рый используется только для решения уравнений гиперболич. типа (он нашел широкое применение при решении задач газовой динамики).
Методы второй группы дают собственно разностные схемы. Пусть, напр., имеется гиперболич. уравнение
где Аесть 
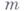
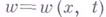

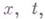
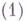
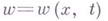
где 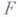
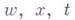
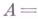
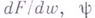
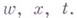
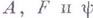
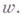
с соответствующими краевыми условиями.
где 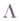


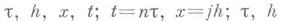
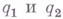
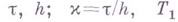
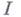
где 
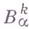

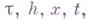


По свойствам аппроксимации разностные схемы можно подразделить на два класса: условно аппроксимирующие и абсолютно аппроксимирующие. Условно аппроксимирующие разностные схемы аппроксимируют исходное дифференциальное уравнение при 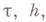

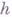
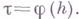

В случае условной аппроксимации разностное уравнение может аппроксимировать различные дифференциальные уравнения при различных законах предельного перехода. Так, напр., для уравнения
рассмотрим две разностные схемы:
При законе предельного перехода
разностная схема (3) аппроксимирует уравнение (2), а при законе предельного перехода
Разностная схема (4) аппроксимирует уравнение (2) абсолютно.
Аналогично, разностные схемы подразделяются на условно устойчивые п абсолютно устойчивые. Так, разностная схема (4) устойчива, если выполнено следующее условие (условие Куранта):
т. е. условно устойчива. С другой стороны, неявная разностная схема
устойчива при любых соотношениях между 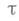
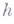
Явные разностные схемы просты в реализации, но являются или условно устойчивыми или условно аппроксимирующими. В случае абсолютно аппроксимирующей разностной схемы условие устойчивости явной схемы имеет, как правило, вид
что приводит к излишне мелкому шагу т и неоправданному увеличению объема вычислений. Абсолютно устойчивые и абсолютно аппроксимирующие схемы находятся только в классе неявных схем.
Неявные разностные схемы более сложны в реализации при переходе с одного временного слоя на другой, но зато шаг 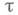
Теоремы сходимости для разностных схем, аппроксимирующих линейные дифференциальные уравнения, позволяют сводить исследование сходимости разностной схемы к исследованию ее устойчивости.
Для разностных схем, аппроксимирующих гиперболич. уравнения с постоянными коэффициентами, устойчивость исследуется методом Фурье, а именно, оценивается норма образа Фурье оператора шага разностной схемы. Так как спектральный радиус матрицы сираза Фурье оператора шага не превосходит нормы матрицы, то отсюда следует необходимый критерий устойчивости: для устойчивости разностной схемы необходимо, чтобы спектральный радиус образа Фурье оператора шага не превосходил величины 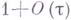
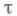
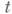
Метод априорных оценок аналогичен соответствующему методу для дифференциальных уравнений, но в разностном случае его реализация встречает большие трудности, что связано со спецификой разностного анализа, в к-ром, в отличие от априорных оценок в теории дифференциальных уравнений, многие соотношения принимают громоздкий вид.
Простейшей мажорантной оценкой является оценка для разностных схем с положительными коэффициентами.
Напр., пусть для уравнения (2) с 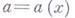
Отсюда следует равномерная устойчивость схемы (5) в пространстве С. Оценка переносится на разностные схемы, аппроксимирующие гиперболич. системы уравнений в инвариантах.
Весьма важный, хотя и ограниченный класс разностных схем составляют разностные схемы с положительными коэффициентами и матрицами (так наз. мажорантные схемы). Если коэффициенты таких разностных схем есть симметричные, положительные матрицы, Липшиц-непрерывные по х, то такие схемы устойчивы в пространстве 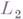
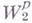
причем функции 
Приведенная оценка доказывает устойчивость разностной схемы (6) и аналогична энергетич. неравенству для системы уравнений акустики.
В основе локально алгебраич. метода лежит изучение свойств локального разностного оператора, получаемого из соответствующего разностного оператора с переменными коэффициентами «замораживанием» коэффициентов. Тем самым анализ устойчивости разностного оператора с переменными коэффициентами заменяется анализом целого семейства операторов с постоянными коэффициентами. Локальный критерий устойчивости является обобщением метода «замораживания» коэффициентов, используемого в теории дифференциальных уравнений.
К локальному критерию устойчивости примыкает диссипативный критерий устойчивости. Разностная схема наз. диссипативной порядка 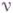
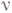

При исследовании устойчивости разностных схем для нелинейных гиперболич. уравнений (в частности, уравнений газовой динамики) применяется метод дифференциального приближения, к-рый заменяет анализ разностной схемы анализом ее дифференциального приближения.
Например, дифференциальное приближение разностной схемы (4) для уравнения (2) строится следующим образом: разложение в (4) функции
в ряды Тейлора относительно точки 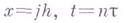

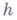
Исключение в (7) производных 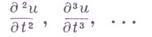
где 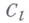
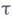

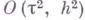
и к П-форме первого дифференциального приближения разностной схемы (4):
Под диссипацией разностной схемы (4) понимается величина
Диссипативные члены в (8) определяют свойства аппроксимационной вязкости схемы (т. е. некоторого механизма сглаживания в разностной схеме). На вид диссипативных членов влияют как искусственные диссипативные члены, вводимые в исходное дифференциальное уравнение, так и структура самой разностной схемы. Первое дифференциальное приближение дает главный член аппроксимационной вязкости. Метод дифференциального приближения широко используется при исследовании разностных схем для нелинейных уравнений и позволяет объяснить эффекты неустойчивости разностных схем, наблюдаемые в конкретных расчетах и не улавливаемые локально методом Фурье.
Основой построения разностных схем в многомерных случаях являются методы расщепления (слабой аппроксимации) и дробных шагов, позволяющие сводить интегрирование исходного многомерного уравнения к интегрированию уравнений более простой структуры (см. Дробных шагов метод).
Получают развитие методы решения гиперболич. уравнений, основанные на методе конечных элементов, к-рый можно рассматривать как разностный метод на специальной нерегулярной сетке.
Лит.:[1] Годунов С. К., Рябенький В. С., Разностные схемы, М., 1973; [2] Рихтмайер Р., Мортон К., Разностные методы решения краевых задач, пер. с англ., М., 1972; [3] Рождественский Б. Л., Яненко Н. Н., Системы квазилинейных уравнений. М., 1968; [4] Самарский А. А., Гулин А. В., Устойчивость разностных схем, М., 1973; [5] Яненко Н. Н., Шокин Ю. И., «Сиб. матем. т.», 1969, т. 10, № 5, с. 1173-87; [6] Сердюкова С. И., «Докл. АН СССР», 1973, т. 208, № 1, с. 52-55. Ю. И. Шокун, Н. Н. Яненко.