Как решать геометрические задачи

Как решать задачи по геометрии. Часть 1

Геометрическая логика при решении задач

Геометрия… Страшное слово для бесчисленного множества учеников. Они знают свойства фигур и выучили определения и теоремы, но задачи по геометрии все равно остаются какой-то китайской грамотой.

Это про тебя? Тогда ты попал туда, куда нужно!

Проблема подавляющего большинства учеников в том, что они не умеют обдумывать задачу по геометрии. Их этому не научили (ну, или они не захотели научиться, когда была возможность). Именно в этой статье, я объясню саму технологию обдумывания и, в конечном счете, нахождения решения ПРАКТИЧЕСКИ ЛЮБОЙ задачи по геометрии.

Ты играл когда-нибудь в квесты? Неважно в реальной жизни или в компьютере. Во всех квестах принцип один – у тебя есть что-то (вещи, знания, навыки) и есть цель (раскрыть какую-нибудь тайну, найти некий предмет, «спасти принцессу» и т.д.). При этом путь к цели – неизвестен. И зачем нужны эти самые имеющиеся у тебя «вещи, знания, навыки» – тоже непонятно. Что делать? Как достичь цели?

Известно как: использовать то, что есть, и искать, куда это применить, чтоб продвинуться к цели. То есть, делать шаги от своего текущего местонахождения – к цели. При этом понятно, что некоторые шаги будут вести нас не туда, куда надо, а совсем даже в тупик. А иногда мы будем находить вещи или информацию, вроде бы напрямую к цели не ведущие, но как выяснится в дальнейшем – необходимую.

Более того, порой можно логически двигаться и наоборот – от цели к твоей текущей позиции. Например, если нужно «спасти принцессу из замка», то понятно, что, скорее всего, надо будет как-то попасть в замок. А для этого надо оказаться на острове, где этот замок стоит. Как попасть? Может быть на лодке. Или найти телепорт. Или использовать магию. Но на остров – надо. Начинаем искать пути на остров. Это уже логические шаги от цели к текущей позиции.

Ладно, давай уже конкретный пример разберем.

Задача. В треугольнике \(ABC\) из точки \(B\) проведена высота \(BH\). Найти длину отрезка \(AH\), если известно, что сторона \(AC\; =\; 14\) см и угол \(A\) равен углу \(C\).

Так. С чего начинается решение геометрической задачи? Ну, а с чего начинается решение квеста? Правильно, осматриваемся по сторонам, изучаем, что у нас есть и куда нас жизнь закинула.

В геометрии это означает:

Хорошо. Значит, текущая ситуация у нас такова:

Давайте потихоньку развеивать туман. Нам известно, что углы \(А\) и \(С\) равны, а это значит, что треугольник \(АВС\) – равнобедренный с основанием АС (теория – «признак равнобедренного треугольника: равенство углов при одной из сторон. Она и является основанием»). Это новая информация, новые данные, изначально неизвестные. Делаем шаг.

Отлично. Теперь смотрим, что у нас есть еще? Еще у нас есть информация, что \(BH\) – высота. А раз треугольник \(ABC\) – равнобедренный, то значит \(BH\) еще и медиана (теорема о высоте в равнобедренном треугольнике: высота, проведенная к основанию равнобедренного треугольника является медианой и биссектрисой). То есть, мы, используя новые, полученные на предыдущем шаге данные, а также исходные данные и знание теории, делаем еще один шаг и опять получаем новую информацию.

А что мы знаем про медиану? Она делит противоположную сторону на две равные части (определение медианы: отрезок, соединяющий вершину треугольника с серединой противоположной стороны). Но тогда получается, что точка \(H\) делит сторону \(AC\) пополам. То есть \(AH = HC\).

Стоп. Так у нас же есть длина стороны \(AC\)! И если мы знаем, что точка \(H\) делит сторону \(AC\) пополам, значит, \(AH\) равен половине \(AC\)! Таким образом, получаем, что \(AH = AC/2 = 14/2=7\) см.

Готово. Ответ получен.

Естественно, такие конструкции с «пятном тумана» рисовать каждый раз не нужно, эта схема показывает логическую цепочку решения у нас в голове. А записывается примерно так:

Источник

Как решать задачи по геометрии. Часть 1

Геометрическая логика при решении задач

Геометрия… Страшное слово для бесчисленного множества учеников. Они знают свойства фигур и выучили определения и теоремы, но задачи по геометрии все равно остаются какой-то китайской грамотой.

Это про тебя? Тогда ты попал туда, куда нужно!

Проблема подавляющего большинства учеников в том, что они не умеют обдумывать задачу по геометрии. Их этому не научили (ну, или они не захотели научиться, когда была возможность). Именно в этой статье, я объясню саму технологию обдумывания и, в конечном счете, нахождения решения ПРАКТИЧЕСКИ ЛЮБОЙ задачи по геометрии.

Ты играл когда-нибудь в квесты? Неважно в реальной жизни или в компьютере. Во всех квестах принцип один – у тебя есть что-то (вещи, знания, навыки) и есть цель (раскрыть какую-нибудь тайну, найти некий предмет, «спасти принцессу» и т.д.). При этом путь к цели – неизвестен. И зачем нужны эти самые имеющиеся у тебя «вещи, знания, навыки» – тоже непонятно. Что делать? Как достичь цели?

Известно как: использовать то, что есть, и искать, куда это применить, чтоб продвинуться к цели. То есть, делать шаги от своего текущего местонахождения – к цели. При этом понятно, что некоторые шаги будут вести нас не туда, куда надо, а совсем даже в тупик. А иногда мы будем находить вещи или информацию, вроде бы напрямую к цели не ведущие, но как выяснится в дальнейшем – необходимую.

Более того, порой можно логически двигаться и наоборот – от цели к твоей текущей позиции. Например, если нужно «спасти принцессу из замка», то понятно, что, скорее всего, надо будет как-то попасть в замок. А для этого надо оказаться на острове, где этот замок стоит. Как попасть? Может быть на лодке. Или найти телепорт. Или использовать магию. Но на остров – надо. Начинаем искать пути на остров. Это уже логические шаги от цели к текущей позиции.

Ладно, давай уже конкретный пример разберем.

Задача. В треугольнике \(ABC\) из точки \(B\) проведена высота \(BH\). Найти длину отрезка \(AH\), если известно, что сторона \(AC\; =\; 14\) см и угол \(A\) равен углу \(C\).

Так. С чего начинается решение геометрической задачи? Ну, а с чего начинается решение квеста? Правильно, осматриваемся по сторонам, изучаем, что у нас есть и куда нас жизнь закинула.

В геометрии это означает:

Хорошо. Значит, текущая ситуация у нас такова:

Давайте потихоньку развеивать туман. Нам известно, что углы \(А\) и \(С\) равны, а это значит, что треугольник \(АВС\) – равнобедренный с основанием АС (теория – «признак равнобедренного треугольника: равенство углов при одной из сторон. Она и является основанием»). Это новая информация, новые данные, изначально неизвестные. Делаем шаг.

Отлично. Теперь смотрим, что у нас есть еще? Еще у нас есть информация, что \(BH\) – высота. А раз треугольник \(ABC\) – равнобедренный, то значит \(BH\) еще и медиана (теорема о высоте в равнобедренном треугольнике: высота, проведенная к основанию равнобедренного треугольника является медианой и биссектрисой). То есть, мы, используя новые, полученные на предыдущем шаге данные, а также исходные данные и знание теории, делаем еще один шаг и опять получаем новую информацию.

А что мы знаем про медиану? Она делит противоположную сторону на две равные части (определение медианы: отрезок, соединяющий вершину треугольника с серединой противоположной стороны). Но тогда получается, что точка \(H\) делит сторону \(AC\) пополам. То есть \(AH = HC\).

Стоп. Так у нас же есть длина стороны \(AC\)! И если мы знаем, что точка \(H\) делит сторону \(AC\) пополам, значит, \(AH\) равен половине \(AC\)! Таким образом, получаем, что \(AH = AC/2 = 14/2=7\) см.

Готово. Ответ получен.

Естественно, такие конструкции с «пятном тумана» рисовать каждый раз не нужно, эта схема показывает логическую цепочку решения у нас в голове. А записывается примерно так:

Источник

Как научиться хорошо и быстро решать задачи по геометрии

Как подружиться с геометрией, если предмет кроме страха, других эмоций не вызывает? Этим вопросом с одинаковой частотой задаются как сами ученики, так и их родители. Многим, сложно преодолеть психологический барьер и начать просто вникать в тему. О том, как правильно подойти к изучению, этого, действительно сложного предмета, в нашей статье.

Распространенная причина страха

На 90% отношение к предмету формирует преподаватель. Если он сумеет пробудить в детях живой интерес – в геометрии начнут разбираться даже самые закоренелые троечники. Дети будут готовы оставаться на перемене в классе, только чтобы рассмотреть еще один вариант решения задачи.

Если же, предмет объясняется скучно, непонятно, вникнуть в тему будет сложно. В таких случаях, рекомендуем воспользоваться нижеописанными советами.

С чего начать изучение

Первое, что нужно сделать, перед тем, как погрузиться в изучение предмета – осознать, за один день ничего не произойдет. Процесс обучения займет определенное количество времени. Сколько конкретно, зависит от поставленной цели. Если в планах просто хорошая оценка на экзамене, или нужно написать контрольную, достаточно изучить конкретную тему и немного попрактиковаться.

Вникнуть в предмет: рабочие приемы

Пролистайте в учебнике несколько последних параграфов. Спешить не нужно, старайтесь вникнуть в написанное. После, попытайтесь решить несколько задач. Постоянно возвращайтесь к тексту в учебнике, постарайтесь самостоятельно «увидеть» алгоритм решения задачи.

Если первое время, испытываете какие-либо затруднения, ничего страшного. Главное, не опускать руки, и проявить упорство. Загляните в выпущенный к учебнику, решебник, но не просто списывайте готовые решения, а попытайтесь ухватить логику алгоритма. Если подобную задачу рассматривали на уроке, попробуйте вспомнить, что говорил учитель по этой теме. Возможно, что-то из озвученного им, пригодится.

Не пренебрегайте помощью сверстников. Иногда, одноклассники, друзья, сестры или братья, могут донести суть изучаемой темы гораздо быстрее, чем это сделал бы взрослый человек.

Другое дело, если перед учеником стоит задача более глубокого погружения в предмет. Усилий потребуется гораздо больше, и опять, на первом месте будет стоять мотивация и осознание, того, что придется потрудиться. Помните! Решить одну задачу самостоятельно, а потом скатиться к систематическому списыванию из интернета готовых решений, не поможет. Упражняться в решении следует систематически и довольно часто. Прекрасно, если полчаса или даже час в день, вы будете посвящать исключительно геометрии.

Достичь поставленной цели и овладеть предметом на должном уровне поможет только практика. Пусть решение 1-2 задачек в день, станет привычкой. Со временем, вы отметите про себя, что процесс решения идет все легче, а находить правильные ответы становится интереснее.

Если на уроке рассматривается задача и учитель предлагает желающим попробовать решить ее у доски, отзывайтесь, даже пока не видите, как ее осилить. Начните рассуждать. Преподавателям всегда приятно, когда ученик искренне интересуется предметом. Учитель обязательно включится в ваши рассуждения. Там, где нужно, поможет. Направит ход мыслей в нужном направлении. Вы запомните алгоритм, и в следующий раз с блеском справитесь самостоятельно.

Использовать по желанию

Если геометрия не дается ни в какую или требуется понимание предмета, выше школьного уровня, можно провести несколько занятий с репетитором. Индивидуальные занятия с преподавателем практически всегда дают хороший результат. Репетитору даже не обязательно посещать лично. Организовать уроки, при современных технологиях, возможно по скайпу или через другие подобные приложения.

Вот и все рекомендации. Ничего сложного, а польза огромная. Просто выполняйте их, и вы даже не заметите, как серьезно продвинетесь в геометрии.

Источник

«Классические» схемы для решения задач по геометрии

Так ли это? Может быть, и в планиметрии есть схемы, на которых строится множество задач?

Да, есть. Я называю их «классические схемы планиметрии». Учимся узнавать их и использовать в задачах! И возможно, что на ЕГЭ вам встретится задача, «ключиком» к которой будет одна из этих схем. Конечно, на ЕГЭ эти утверждения надо доказывать.

Вот 5 полезных схем для решения задач по планиметрии.

Схема 1. В треугольнике АВС проведены высоты АМ и СК.

H – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК

1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если , и , если

Схема 2. Пусть луч МА пересекает окружность в точках А и В, а луч МD – в точках С и D, причем МА > МВ, МD > МС. Тогда треугольники ВМС и DМА подобны.

Схема 3. У треугольников АВС и АМС сторона АС – общая, угол В равен углу М, причем точки В и М лежат по одну сторону от прямой АС. Тогда точки А, В, С, М лежат на одной окружности.

Схема 4. У треугольников АВС и АМС сторона АС – общая, углы В и М – прямые. Тогда точки А, В, С, М лежат на окружности, радиус которой равен половине АС.

Схема 5. Лемма о трезубце (трилистнике)

И несколько лайфхаков для сдающих ЕГЭ.

2) Когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур – у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. В каких формулах он встречается? – Правильно, в теореме синусов и в одной из формул для площади треугольника.

3) Есть такие теоремы, которые вроде и входят в школьную программу – а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы треугольника. А вы их знаете?

4) Как научиться решать задачи по геометрии? Если у вас маловато опыта – не стоит начинать с реальных задач ЕГЭ. Сначала – задачи на доказательство. Тем более что в реальной задаче 16 из варианта ЕГЭ первый пункт – доказательство.

5) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. А это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б).

6) Среди стратегий подготовки к ЕГЭ есть эффективные. А есть откровенно проигрышные.

Пример плохой стратегии – когда старшеклассник принимает решение заниматься только алгеброй и считает планиметрию и тем более стереометрию слишком сложными для себя. И вот на ЕГЭ попадается сложное неравенство или «экономическая» задача. И всё, баллов не хватает! Тех самых баллов за планиметрию и стереометрию, которые можно было взять, не хватает для поступления!

Чтобы такого не случилось – занимаемся планиметрией как можно больше.

7) Стоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.

Источник

Осваиваем простые приемы решения геометрических задач

Идея I

Если в четырехугольнике суммы противоположных углов равны 180°, то вокруг этого четырехугольника можно описать окружность.

Задача. Дан прямоугольный треугольник ABC. На катете АС выбрана произвольная точка М. Из точки М опущен перпендикуляр MN на гипотенузу. Докажите, что углы MCN и MBN равны.

Решение. Угол MNB — прямой. По условию, треугольник ABC прямоугольный, значит, есть еще один прямой угол. Обратим внимание на четырехугольник MNBC: в нем есть два противолежащих прямых угла, их сумма равна 180°. Следовательно, вокруг четырехугольника MNBC можно описать окружность. Углы, равенство которых нужно доказать, опираются на одну дугу MN и являются вписанными. Два вписанных угла опираются на одну и ту же дугу, значит, они равны.

Идея II

Если известен угол треугольника, можно найти угол между биссектрисами, обращенными в сторону этого угла.

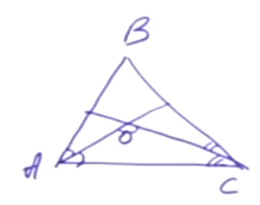
Задача. Дан треугольник ABC. Проведены биссектрисы углов A и С, они пересекаются в точке O. Найдите угол AOC (т.е. есть угол между биссектрисами).

Решение. Известно, что ∠ABC = ∠В. Эту задачу легко решить с помощью теоремы суммы углов треугольников. ∠A + ∠C = 180° – ∠B. Суммы половинок углов А и С равны 90° – ½ ∠B. Тогда ∠AOC = 90° + ½ ∠B.

Совмещение идей I и II

Некоторые задачи находятся как бы на пересечении нескольких идей решения.

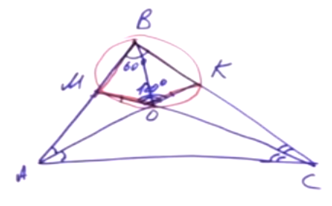
Задача. Дан треугольник ABC. Известно, что угол В равен 60°. Проведены биссектрисы углов: АК и СМ, они пересекаются в точке О. Докажите, что отрезок ОМ равен отрезку ОК.

Решение. Найдем угол АОС по формуле 90° + ½ ∠B. ∠В = 120°. Обращаем внимание на четырехугольник МВКО. В нем сумма противоположных углов равна 180°, значит, вокруг него можно описать окружность. О — точка пересечения биссектрис треугольника АВС. Следовательно, луч ВО делит угол АВС пополам. ∠МВО = ∠ОВК. Данные углы являются вписанными, значит, равны и дуги, на которые они опираются. Дуга МО равна дуге ОК. Известно, что равные дуги стягивают равные хорды. Хорда ОМ равна хорде ОК.

Идея III

Если из двух точек, лежащих в одной полуплоскости, отрезок между двумя другими точками виден под одним и тем же углом, то эти 4 точки лежат на одной окружности.

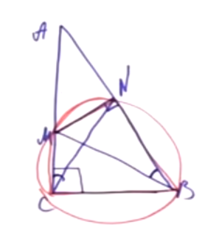
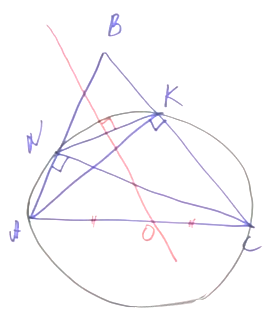
Задача. Дан остроугольный треугольник АВС. Проведены две высоты: АК и СN. Докажите, что серединный перпендикуляр отрезка NK пересекает отрезок АС в середине (точка О является серединой отрезка АС).

Решение. ∠ANC = ∠AKC. Мы можем нарисовать окружность вокруг четырехугольника ANKC. Отрезок NK является в этой окружности хордой, а АС — диаметром, поскольку он виден из точек N и K под прямым углом. Серединный перпендикуляр проведен к хорде, он содержит диаметр окружности. Два диаметра пересекаются в центре окружности. О — это центр окружности. АО и ОС — это диаметры. Следовательно, АО = ОС.

Идея IV

Если в треугольнике продлить медиану и построить параллелограмм, можно извлечь много дополнительных данных для решения задачи.

Задача. Дан треугольник АВС и его медиана ВМ. Известно, что ВМ в два раза меньше стороны АВ. Докажите, что угол МВС равен сумме ∠А + ∠С.

Решение. Воспользуемся построением параллелограмма. Проведем МК. BM = ½ ВК. Следовательно, АВ = ВК. В этом случае треугольник АВК является равнобедренным. В равнобедренном треугольнике углы при основании равны, значит, ∠ВАК = ∠ВКА. ∠КАМ = ∠С. ∠АКВ = ∠СВК. Из этого мы получаем необходимое равенство.

Совмещение идей III и IV

Задача. Дан треугольник АВС, в котором проведена медиана ВМ. На медиане ВМ выбрана точка К так, что ∠ВАС = ∠АКМ. Докажите, что ∠ АСВ = ∠МКС.

Решение. Продлим медиану на ее длину и получим точку N. BM = MN. ABCN — параллелограмм. ∠BAC = ∠ACN. Из точек К и С, лежащих по одну сторону от прямой, видим отрезок AN под одним и тем же углом. Вокруг четырехугольника AKCN описываем окружность. Поскольку ABCN — параллелограмм, ∠NAC = ∠BCA. Но углы NAC и NKC являются вписанными, опирающимися на одну дугу. Следовательно, ∠NAC = ∠NKC. Так мы доказали, что ∠МКС = ∠МСВ.

Идея V

Если в прямоугольном треугольнике АВС проведена медиана из вершины прямого угла, то медиана СМ будет равняться половине гипотенузы АВ. То есть СМ = АМ = МВ.

Задача. Дан треугольник АВС. На внешние стороны построены два прямоугольных треугольника: ADB и BEC. Докажите что отрезок DE, соединяющий вершины прямых улов, не больше полпериметра треугольника АВС.

Решение. Проведем медианы через точки M и N (середины сторон АВ и ВС). Соединим точки, образовав четырехугольник DENM. Звено ломаной DE не превосходит сумму длин отрезков DM + MN + NE. DE ≤ DM + MN + NE = ½ АВ + ½ АС + ½ ВС. Следовательно, DE ≤ ½ Р_авс

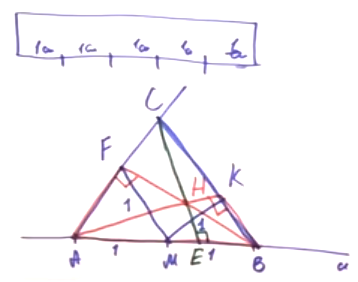
Факт, обратный данному. Если в треугольнике АВС медиана СМ равна половине стороны АВ, значит, АСВ = 90°. Т.е. если в треугольнике медиана равна половине стороны, к которой она проведена, то этот треугольник является прямоугольным. Рассмотрим эту идею, продемонстрировав также, как только с помощью линейки можно решить задачу на построение перпендикуляра к данной прямой.

Возьмем линейку с ценой деления 1 см. Отложим отрезки: точки А, М и В, так, что АМ = МВ = 1 см. Развернув линейку, поставим точку F (MF = 1 см) и точку К (МК = 1 см). С помощью линейки соединим A и F, B и K и продлим прямые до пересечения в точке С. На рисунке виден треугольник АFВ. FM в нем медиана, равняющаяся половинке стороны. Следовательно, угол F — прямой. Таким же свойством обладает треугольник АКВ. В треугольнике АСВ отрезки АК и ВF являются высотами. Значит, точка H в пересечении высот является центром треугольника. Если соединить СН и продлить в СЕ, это тоже будет высота треугольника АВС. Следовательно, СЕ перпендикулярно АВ. Так, только с помощью линейки мы провели прямую, перпендикулярную данной.

В учебниках авторства Мерзляка А.Г., Полонского В.Б. и Якира М.С. образцовые задачи, демонстрирующие ту или иную идею решения, выделены и обозначены изображением ключа.

Источник