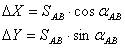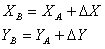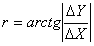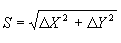Как решать геодезические задачи

Что такое обратная и прямая геодезическая задача: суть, методы решения, назначение

В строительстве большую часть времени занимают геодезические работы. Это комплекс различных измерений и вычислений на местности. Стоит ли говорить, что качество выполненных работ зависит от точности полученных результатов. Это влияет на размещение зданий и сооружений, а также возведение их конструктивных элементов. Все должно соответствовать проектным показателям и техническим регламентам. Геодезические работы выполняются в объеме, определенном особенностями объекта и стадией его реализации. Компания «Промтерра» специализируется на их проведении с составлением необходимых чертежей, схем и расчетов. Для этого есть все составляющие: действующая лицензия, опыт, допуск СРО, штат специалистов. Один из вопросов, который поступает при выполнении работ, касается геодезической задачи. Что это такое, как используется в работе и ее назначение.

Математика в действии

По своей сути геодезические задачи — это математика в чистом виде. Основная задача состоит в определении взаимного положения точек принадлежащих какой-либо поверхности. Наиболее часто приходится иметь дело с прямыми и обратными геодезическими задачами, но на этом математические вычисления не заканчиваются. В зависимости от поставленных условий могут применяться и другие виды. Например, решение треугольника по измеренным углам и сторонам. Интересный исторический факт: с геодезическими задачами исследователи этой темы работают уже больше трех веков, а споры относительно методов дальше продолжаются.

Что такое прямая геодезическая задача

Эта разновидность предполагает вычисление координат, то есть широты и долготы определенной точки. А она, в свою очередь, лежит на математически правильной поверхности — земном эллипсоиде. Вычисления производятся по координатам другой точки, по длине и азимуту геодезической линии. Точность решения зависит от корректности исходных данных. Для проведения вычислений используют формулы нахождения приращений и определения координат.

Специалисты применяют разные методы для получения результатов. Наиболее востребованными считаются косвенный и прямой. Они отличаются тем, что в основе лежит точность исходных данных. Косвенные методы решения очень чувствительны к ним. Если в исходнике есть значительные расстояния, изменения по азимуту, то вычисления не получится сделать, или они будут с большими погрешностями. Прямые методы работают по соотношениям сфероидической геодезии, поэтому результаты можно получить более точные. Кстати, прямой тип геодезических задач применяется при вычислении координат в теодолитном ходе.

Что такое ОГЗ: суть обратной геодезической задачи

При работе над обратной геодезической задачей вычисления проводятся по известным координатам двух точек на земном эллипсоиде. Это нужно для получения значений горизонтального положения линий между ними, а также дирекционного угла этой самой линии. В этом состоит суть. Для получения искомых величин используется вычисление румба и расстояние между координатами точек. Нужно помнить, что дирекционный угол при этом находится по четверти системы координат, которая и является объектом, где размещены искомые позиции. Для решения нужно учитывать знаки приращения, которые свойственны для определенных четвертей. В этом типе задач уделяют большое значение сходимости результатов, поэтому расчеты могут проводиться несколько раз. На это влияют свойства горизонтального положения между точками. В каких случаях применяется обратная геодезическая задача? В тех, когда по известным двум точкам и их координатам определяют расстояние не только между ними, но и дирекционный угол линии.

В том или ином виде геодезические задачи возникают и в других направлениях — в полигонометрии, триангуляции, но на этом не заканчивается востребованность. Используется также, когда стоит задача определения взаимного положения точек по исходным данным длины и направления соединяющей линии. Есть ряд случаев, когда геодезические задачи решают с использованием формул аналитической геометрии в пространстве. Речь идет о пространственных прямоугольных координатах. Для этого используют пространственные компоненты направления прямой линии между этими точками.

Обратный тип геодезической задачи — не просто математическая проверка и вычисления. Она имеет практическое значение, ведь используется при вычислении длин проектных линий. Кроме этого, используется при выполнении привязки теодолитных ходов к пунктам геодезической сети, съемочных сетей и сетей сгущения. Еще одно практическое назначение — определение направления с пункта на пункт при отсутствии видимости. Обратная геодезическая задача используется в промышленном и гражданском строительстве.

А как решать обратные задачи, если в исходнике большие расстояния? В этом случае рекомендуется использовать метод итерации. Его можно использовать при расстояниях до 20 000 км. Итерация основана на решении прямой геодезической задачи любым выбранным методом — численным или аналитическим. И точность решения именно ОГЗ определяется решением ПГЗ.

Прямые и обратные геодезические задачи требуют получения точных результатов. Насколько получится достичь поставленной цели, зависит от исходных сведений и выбранного метода решения. Вычисление способом Бесселя, методом Рунге-Кутта-Фельберга, итерации, численного интегрирования — в каждом отдельном случае выбор зависит от расстояний и координат точек. В штате компании «Промтерра» работают опытные специалисты в сфере инженерной геодезии, поэтому за решение даже самых сложных задач можно быть спокойными. Тема геодезических задач всегда остается актуальной, поэтому отслеживание последних тенденций в проведении вычислений для получения точных результатов — необходимость. Важно отметить, что подобного плана математические методы востребованы не только в геодезической сфере деятельности, но и в навигации, корректировке ракетного огня и др.

Источник

Прямая и обратная геодез задачи

Геодезическая задача – математического вида задача, связаная с определением взаимного положения точек земной поверхности и подразделяется на прямую и обратную задачу.

Обратная геодезическая задача (ОГЗ) заключается в определении по геодезическим координатам двух точек на земном эллипсоиде длины и дирекционного угла направления между этими точками.

В зависимости от длины геодезической линии, соединяющей рассматриваемые точки, применяются различные методы и формулы, разработанные в геодезии. По размерам принятого земного эллипсоида (см. Эллипсоид Красовского) составляются таблицы, облегчающие решение геодезических задач и рассчитанные на использование определённой системы формул.

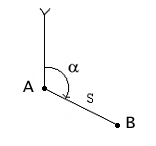
Для определения координат точки в прямой геодезической задаче обычно применяют формулы:

1) нахождения приращений :

2) нахождения координат :

В обратной геодезической задаче находят дирекционный угол и расстояние:

1) вычисляют румб по формуле :

2) находят дирекционный угол в зависимости от четверти угла :

3) определяют расстояние между точками :

Геодезическая задача в том и другом виде возникает при обработке полигонометрии и триангуляции, а также во всех тех случаях, когда необходимо определить взаимное положение двух точек по длине и направлению соединяющей их линии или же расстояние и направление между этими точками по их геодезическим координатам. В ряде случаев геодезические задачи решают в пространственных прямоугольных координатах по формулам аналитической геометрии в пространстве. В этих случаях вместо длины и дирекционного угла, соединяющей две точки, используют длину и пространственные компоненты направления прямой линии между этими точками.

Тахетрическая съемка

Тахеометрическая съемка – топографическая съемка, выполняемая с помощью теодолита или тахеометра и дальномерной рейки (вехи с призмой), в результате которой получают план местности с изображением ситуации и рельефа.

Тахеометрическая съемка выполняется самостоятельно для создания планов или цифровых моделей небольших участков местности в крупных масштабах (1: 500 – 1: 5000) либо в сочетании с другими видами работ, когда выполнение стереотопографической или мензульной съемокэкономически нецелесообразно или технически затруднительно. Ее результаты используют при ведении земельного или городского кадастра, для планировки населенных пунктов, проектирования отводов земель, мелиоративных мероприятий и т.д. Особенно выгодно ее применение для съемки узких полос местности при изысканиях трасс каналов, железных и автомобильных дорог, линий электропередач, трубопроводов и других протяженных линейных объектов.

Слово «тахеометрия» в переводе с греческого означает «быстрое измерение». Быстрота измерений при тахеометрической съемке достигается тем, что положение снимаемой точки местности в плане и по высоте определяется одним наведением трубы прибора на рейку, установленную в этой точке. Тахеометрическая съемка выполняется обычно с помощью технических теодолитов или тахеометров.

При использовании технических теодолитов сущность тахеометрической съемки сводится к определению пространственных полярных координат точек местности и последующему нанесению этих точек на план. При этом горизонтальный угол B между начальным направлением и направлением на снимаемую точку измеряется с помощью горизонтального круга, вертикальный угол v – вертикального круга теодолита, а расстояние до точки D – дальномером. Таким образом, плановое положение снимаемых точек определяется полярным способом (координатами в,d), а превышения точек – методом тригонометрического нивелирования.

Преимущества тахеометрической съемки по сравнению с другими видами топографических съемок заключаются в том, что она может выполняться при неблагоприятных погодных условиях, а камеральные работы могут выполняться другим исполнителем вслед за производством полевых измерений, что позволяет сократить сроки составления плана снимаемой местности. Кроме того, сам процесс съемки может быть автоматизирован путем использования электронных тахеометров, а составление плана или ЦММ – производить на базе ЭВМ и графопостроителей. Основным недостатком тахеометрической съемки является то, что составление плана местности выполняется в камеральных условиях на основании только результатов полевых измерений и зарисовок. При этом нельзя своевременно выявить допущенные промахи путем сличения плана с местностью.

Источник

Через всю географию: навигационные и геодезические задачи на разных языках

Приветствую вас, глубокоуважаемые!

«… истинное место судна хотя и неизвестно, но оно не случайно, оно есть, но неизвестно в какой точке» Алексишин В. Г. и др. Практическое судовождение, 2006. стр. 71

«С двух краев галактики вышли пешеходы. » (С) Сергей Попов (Астрофизик)

В свете новых тенденций стиля арт-нуво я хотел написать о решении геодезических задач на плоской земле. Но пока еще заявление о том, что форма земли удобно аппроксимируется эллипсоидом не является ересью и крамолой, предлагаю всем интересующимся приобщиться к более консервативным моделям.

А это, релевантная КДПВ:

Для тех, кто спешит (я и сам такой), вот репозиторий на GitHub, где лежат все исходники с тестами и примерами.

Репозиторий организован очень просто: библиотека на данный момент представлена на трех языках и каждая реализация лежит в своей папке:

Чтобы посмотреть, как все работает, с какими параметрами вызывает и что возвращает, и провести разведку боем, есть разные демки и тесты:

Почти всегда углы — в радианах, расстояния в метрах, время в секундах.

Теперь, начнем, пожалуй, с начала:

Геодезические задачи

Есть две типовые геодезические задачи: прямая и обратная.

Если например, я знаю свои текущие координаты (широту и долготу), а потом прошагал 1000 километров строго на северо-восток, ну или на север. Какие теперь у меня будут координаты? — Узнать, какие у меня будут координаты — значит решить прямую геодезическую задачу.

То есть: Прямая геодезическая задача — это нахождение координат точки по известной, дистанции и дирекционному углу.

С обратной задачей все совсем понятно — например, я определил свои координаты, а потом прошагал сколько-то по прямой и снова определил свои координаты. Найти, сколько я прошел — значит решить обратную геодезическую задачу.

То есть: Обратная геодезическая задача — это нахождение расстояния между двумя точками с известными географическими координатами.

Решать эти задачи можно несколькими способами, в зависимости от необходимой точности и времени, которое вы готовы на это потратить.

Самый простой способ — представить что земля плоская — это сфера. Давайте попробуем.
Вот формула для решения прямой задачи (источник):

Здесь , — широта и долгота исходной точки, — дирекционный угол, отсчитывающийся по часовой стрелке от направления на север (если смотреть сверху), — угловое расстояние d/R. d — измеренное (пройденное) расстояние, а R — радиус земли. , — широта и долгота искомой точки (ту, в которую мы пришли).

Для решения обратной задачи есть другая (не менее простая формула):

Где , и , -координаты точек, R — земной радиус.

Описанные формулы называются Haversine Equations.

Очевидно, что здесь есть какой-то подвох: земля не сфера, а плоскость и это как-то должно отражаться на применимости этих формул и/или на точности решения.

И действительно. Но для того, чтобы определиться с этим, нужно с чем-то сравнивать.
Еще в 1975 году Тадеуш Винценти (Thaddeus Vincenty) опубликовал вычислительно эффективное решение прямой и обратной геодезической задач на поверхности сфероида (известного более под ником Эллипсоид Революции, товарищ! Эллисоид Вращения), ставшее почти стандартом.

Описание устройства метода тянет на отдельную статью, поэтому я ограничусь лишь отсылкой на оригинальную работу Винценти и на онлайн-калькулятор с описанием алгоритма.

В библиотеке UCNLNav решение прямой и обратной геодезической задач по формулам Винценти лежит в следующих функциях:

Самое важное отличие — данные формулы выполняют решение на сфероиде, и его параметры нужно передавать в функции. Для этого есть простая стуктура, которая его описывает.

Во всех реализациях можно в одну строчку получить один из стандартных эллипсоидов. (Сплошь и рядом применяется WGS84 [https://en.wikipedia.org/wiki/World_Geodetic_System] и его приведем в качестве примера):

Для того, чтобы понять, чего нам будет стоить применение решений для сферы вместо эллипса, реализации на Matlab присутствует скрипт.

В Matlab безумно удобно отображать всякое без лишних телодвижений, поэтому я выбрал его для демонстрации.

Логика его работы скрипта:

1. Берем точку с произвольными координатами

и произвольное направление (я выбрал примерно на запад):

2. Шагаем от нее на все увеличивающуюся дистанцию. Для чего сразу задаемся числом шагов и размером шага:

3. Для каждого шага решаем прямую геодезическую задачу на сфере и на эллипсоиде, получая искомую точку:

4. Для каждого шага решаем обратные геодезические задачи — вычисляем расстояния между результатами, полученными на сфере и эллипсоиде:

5. Проверяем прямые решения обратными для обоих методов:

В скрипте эта последовательность выполняется сначала для шага = 1000 м, а потом для шага = 1 метр.

Сначала посмотрим, насколько отличаются результаты прямых решений по координатам (широте и долготе), для чего вычислим векторы «дельт», благо на Matlab все пишется в одну строчку:

По оси абцисс будем отображать в логарифмическом масштабе, т.к. у нас расстояния меняются от 1 до 10000 км:

В результате получаем такие графики для широты:

Я плохо понимаю в градусах, всегда руководствуюсь методом для прикидки «на глазок»:
1° чего-нибудь это в среднем 100-110 км. И если ошибка больше миллионной или хотя бы стотысячной части градуса — это плохие новости.

Дальше посмотрим расстояния между исходной точкой и точкой, получаемой на каждом шаге по формулам для сферы и эллипсоида. Расстояние вычислим по формулам Винценти (как заведомо более точным — автор обещает ошибку в миллиметрах). Графики в метрах и километрах это гораздо более осязаемо и привычно:

В результате получаем такую картину:

Получается, что на дальностях 10000 км методы расходятся на 10 км.

Если теперь все повторить для шага в 1000 раз меньше, т.е. когда весь диапазон по оси Х будет не 10000 км а всего 10 км, то картина выходит следующая:

То есть, на дальности 10 км набегает всего 20 метров, а на 1-2 метра формулы расходятся только на дистанциях порядка 1000 метров.

Вывод капитана очевидность: если для задачи точность формул с решением на сфере достаточна, то используем их — они проще и быстрее.

Ну, а для тех, кому миллиметровой точности недостаточно, в 2013 году была опубликована работа с описанием решения геодезических задач с нанометровой (!) точностью. Не уверен, что могу сходу придумать, где такое может понадобится — разве что при геодезических изысканиях при постройке гравитационно-волновых детекторов или чего-то совершенно фантастического ).

Теперь перейдем к самому вкусному:

Решение навигационных задач

На данный момент библиотека умеет определять:

То, что нужно минимизировать, называется функцией невязки.

Для задач TOA она выглядит так:

Где — значение функции невязки для некоей точки с координатами ; N — число опорных точек, имеющих координаты , — измеренные расстояния от опорных точек до позиционируемого объекта.

А для задач TDOA вот так:

Здесь все тоже самое, только рассматриваются разные пары опорных точек и соответствующие времена прихода и , а — скорость распространения сигнала.

А вот так эти функции выглядят в коде:

Как можно видеть, обе функции работают с переменным числом опорных точек или линий. Вообще задачи могут быть разные, и функции невязки тоже.

Например, можно решать задачу не только определения местоположения, но и определения ориентации. В этом случае функция невязки будет содержать один или несколько углов.

Остановимся чуть более подробно на внутреннем устройстве библиотеки

На данном этапе библиотека работает с 2D и 3D задачами и сам решатель не знает и не хочет знать как выглядит минимизируемый функционал. Это достигается следующим способом.

У решателя есть две ипостаси: 2D и 3D решатели, основанные на методе Нелдера-Мида или, как еще его называют, метода Симплекса.

Так как этому методу не требуется вычисление производных (т.н. derivative-free minimization), то в идеале пользователь библиотеки может применять свои собственные функции невязки если такое потребуется. Плюс, теоретически нет никакого верхнего ограничения на количество опорных точек, используемых при решении задачи.

В C# и Rust 2D и 3D Решатели — Generic-методы:

Пример вызова самого решателя:

Все идентично, с точностью до синтаксиса языка.

В Matlabe же, с присущим ему волюнтаризмом, сам решатель понятия не имеет что за базовые элементы ему передаются — пользователь сам должен позаботиться, чтобы передаваемые в решатель ссылка на функцию невязки и набор опорных элементов были совместимы:

И соответственно, вызов решателя выглядит так:

Для демонстрации решения TOA и TDOA задач есть специальный скрипт на Matlab.

Демонстрация в 2D выбрана не случайно — я не уверен что могу придумать, как просто и информативно отобразить трехмерную функцию невязки =)

Итак. В начале скрипта есть параметры, которые можно менять:

Положение искомой точки задается случайным образом в указанной области:

Далее, случайно располагаем опорные точки, вычисляем дистанцию от искомой до них и отображаем все:

В итоге получаем такую картинку:

Добавляем к измерениям дистанций случайные ошибки:

Строим функцию невязки для выбранной области с некоей децимацией — иначе расчеты могут занять ощутимое время. Я выбрал размер области 1000 х 1000 метров и считаю функцию невязки по всей области через 10 метров:

Вот так выглядит функция невязки:

Я конечно немного слукавил — взаимные расположения опорных точек и искомой выбираются так, что они всегда образуют выпуклую фигуру с искомой точкой внутри. Во многом благодаря этому поверхность имеет один минимум, который находится без особых проблем.

Въедливый читатель может изменить этот порядок вещей и попробовать расставить опорные точки и искомую совершенно случайно.

Теперь отобразим все вместе. На поверхности это сделать сложно — разные величины по вертикальной оси. Поэтому удобно все нарисовать на двумерном срезе:

В результате получается примерно так:

В заголовке графика отображается радиальная ошибка — корень из финального значения функции невязки. На графике видно, что реальное местоположение и вычисленное хорошо совпадают, но масштаб не позволяет определить насколько хорошо.

Поэтому отобразим вычисленное местоположение искомой точки и реальное ее местоположение отдельно и посчитаем расстояние между ними:

Вот как это выглядит:

Вспомним, что у нас амплитуда случайной ошибки — 1% от дальности, в среднем дальность

200-400 метров, т.е. амплитуда ошибки составляет порядка 2-4 метров. При поиске решения мы ошиблись всего на 70 сантиметров.

Теперь по аналогии попробуем решить задачу TDOA на тех же данных. Для этого притворимся, что нам известны только времена прихода сигналов с искомой точки на опорные (или наоборот — не принципиально) — просто разделим наши дистанции на скорость распространения сигнала — важны лишь их разности а не абсолютные величины.

Строим и рисуем поверхность ошибок:

Получается что-то такое:

И вид «сверху» с опорными точками, реальным и вычисленным положениями искомой точки:

И более детально, расхождение реального и вычисленного местоположения:

В этом конкретном случае решение по TDOA оказалось даже лучше, чем по TOA — абсолютная ошибка составляет 0.3 метра.

Хорошо в модели — всегда точно знаешь, где фактически расположена искомая точка. На воздухе хуже — может быть несколько точек зрения, под водой ты просто что-то вычислил и все — в 99% случаев, чтобы вычислить отклонение от фактического местоположения, его (это местоположение) тоже сначала надо вычислить.

Теперь, в качестве заключения, объединим наши новые знания про геодезические и навигационные задачи.

Финальный аккорд

Максимально приблизим ситуацию к реальной жизни:

Итак, самый последний тест в библиотеке. В качестве координат искомой точки я выбрал место в парке, где часто гуляю с собакой.

В результате имеем:
Реальное местоположение (Lat, Lon, Z): 48.513724 44.553248 25
Вычисленное положение (Lat, Lon, Z): 48.513726 44.553252 45.6
Расстояние между точками по поверхности (м): 0.389
Разность по координате Z (м): 20.6

Совпадение «в плане» — очень хорошее, ошибка составляет всего 40 сантиметров, а по вертикальной координате — 20 метров. Почему так происходит предлагаю подумать читателям =)

Описываемая библиотека — чисто образовательный проект, который я планирую развивать и пополнять дальше. В планах реализация на C и написание всеобъемлющей документации.

На этом разрешите откланяться, спасибо за внимание. Буду бесконечно рад любому feedback.
Надеюсь, статья и библиотека будут полезны.
Про любые ошибки (грамматические и логические) сообщайте — я исправлю.

На всякий случай приведу здесь ссылку на онлайн (и не только) интерпретаторы Matlab/Octave, которыми пользуюсь сам:

Источник