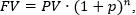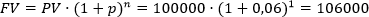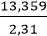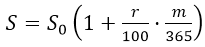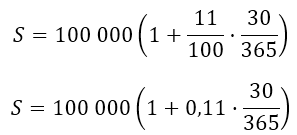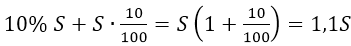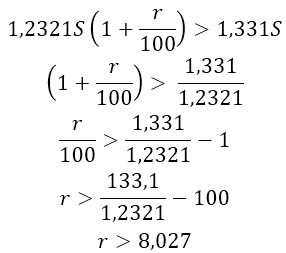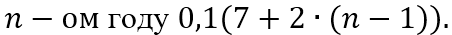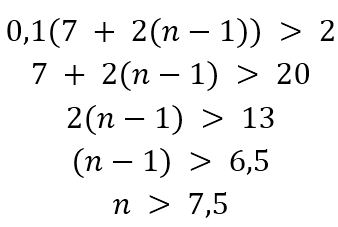Как решать экономические задачи
Задание 15. Финансовая математика — профильный ЕГЭ по математике
Задание 15 Профильного ЕГЭ по математике — «экономическая» задача. Речь, как вы уже поняли, речь пойдет о деньгах. О кредитах и вкладах. О ситуациях, где нужно узнать, при каких значениях переменной будет максимальна прибыль или минимальны издержки. С 2022 года задание 15 оценивается на ЕГЭ в 2 первичных балла.
В этой статье:
Как научиться решать «экономические» задачи. С чего начать,
Две схемы решения задач на кредиты и как их распознать,
В чем основная сложность «экономической задачи»,
Задания на оптимальный выбор. В том числе — с применением производной.
Если материал покажется вам сложным — вернитесь к теме «Задачи на проценты» из первой части ЕГЭ по математике.
Надеемся, что вы уже сейчас сможете ответить на такие вопросы:
Ответы на вопросы, а также подготовительные задачи — в статье «Задача 17 Профильного ЕГЭ по математике. Кредиты и вклады. Начисление процентов». Повторите эту тему.
Запомним, что есть всего две схемы решения задач на кредиты
Первая схема: кредит погашается равными платежами. Или известна информация о платежах. Подробно здесь.
Вторая схема: равномерно уменьшается сумма долга. Или дана информация об изменении суммы долга Подробно здесь.
Посмотрите, чем эти схемы отличаются друг от друга. На какие ключевые слова в условии надо обратить внимание.
Потому что первое, что надо сделать, когда решаете «экономическую» задачу на кредиты или вклады, — определить, к какому типу она относится.
1. 31 декабря 2014 года Аристарх взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Аристарх переводит в банк X рублей. Какой должна быть сумма X, чтобы Аристарх выплатил долг четырьмя равными платежами (то есть за четыре года)?
Конечно, это задача первого типа. Есть информация о платежах. В условии сказано, что Аристарх выплатит долг четырьмя равными платежами.
— коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов,
— сумма ежегодного платежа.
Составим схему погашения кредита. Заметим, что здесь 4 раза (то есть в течение 4 лет) повторяются одни и те же действия:
— сумма долга увеличивается в раз,
Что у нас в скобках? Да, это геометрическая прогрессия, и ее проще записать как
. В этой прогрессии первый член равен 1, а каждый следующий в k раз больше предыдущего, то есть знаменатель прогрессии равен k.
Применим формулу суммы геометрической прогрессии:
И конечно, не спешить возводить эту дробь в четвертую степень или умножать на S = 6902000 рублей.
Ответ: 2296350 рублей
Вот следующая задача.
2. Жанна взяла в банке в кредит 1,8 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?
В этой задаче сумма долга уменьшается равномерно — задача второго типа.
Пусть S — первоначальная сумма долга, S = 1800 тысяч рублей.
Нарисуем схему начисления процентов и выплат. И заметим некоторые закономерности.
Сумма долга уменьшается равномерно. Можно сказать — равными ступеньками. И каждая ступенька равна После первой выплаты сумма долга равна после второй
Последняя в году выплата
Сумма всех выплат в течение первого года:
В первой «скобке» — сумма 12 членов арифметической прогрессии, в которой Обозначим эту сумму
Во второй скобке — также сумма 12 членов арифметической прогрессии, в которой Эту сумму обозначим
Общая сумма выплат за год:
Ответ: 1066500 рублей.
Еще одна задача — комбинированная. Здесь мы рисуем такую же схему выплаты кредита, как в задачах второго типа.
3. В июле 2016 года планируется взять кредит в банке на пять лет в размереSтыс. рублей. Условия его возврата таковы:
− каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить часть долга;
− в июле 2017,2018 и 2019 долг остаётся равным S тыс. рублей;
− выплаты в 2020 и 2021 годах равны по 625 тыс. рублей;
− к июлю 2021 долг будет выплачен полностью.
Найдите общую сумму выплат за пять лет.
Введем переменные: тысяч рублей. Рисуем схему погашения кредита:
Это значит, что и тогда
Но не только задачи на кредиты и вклады могут встретиться в задании 17 Профильного ЕГЭ по математике. Есть еще задачи на оптимальный выбор. Например, нужно найти максимальную прибыль (при соблюдении каких-либо дополнительных условий), или минимальные затраты. Сначала в такой задаче нужно понять, как одна из величин зависит от другой (или других). Другими словами, нужна та функция, наибольшее или наименьшее значение которой мы ищем. А затем — найти это наибольшее или наименьшее значение. Иногда — с помощью производной. А если повезет и функция получится линейная или квадратичная — можно просто воспользоваться свойствами этих функций.
4. Консервный завод выпускает фруктовые компоты в двух видах тары—стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.
| Вид тары | Себестоимость, 1 центнера | Отпускная цена, 1 центнера |
| стеклянная | 1500 руб | 2100 руб |
| жестяная | 1100 руб | 1750 руб |
Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью).
По условию, завод не может выпускать компот только в стеклянных банках или только в жестяных — должны быть и те, и другие.
Общая прибыль завода за сутки равна
Нужно найти наибольшее значение выражения при выполнении следующих условий:
Подставим в выражение для прибыли завода за сутки. Получим, что она равна Это линейная функция от x. Она монотонно возрастает и свое наибольшее значение принимает при Тогда и максимально возможная прибыль завода за день равна
Вот такая она, задача с экономическим содержанием. Мы рассказали о ней самое главное. Если готов осваивать ее самостоятельно — желаем удачи. А если не все будет сразу получаться — приходи к нам в ЕГЭ-Студию на интенсивы, курсы или Онлайн-курс.
Это полезно
В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.
Как подготовиться к решению экономических задач ЕГЭ | 1С:Репетитор
 Лектор, методолог, автор учебных материалов и пособий |
Задание № 17 варианта КИМ ЕГЭ по математике профильного уровня
Текстовая задача с экономическим содержанием – относительно новый вид заданий, появившихся в КИМ ЕГЭ профильного уровня, хотя задачи «на проценты»в вариантах вступительных экзаменов в вузы встречались в «доегэшную пору» достаточно часто, особенно если речь шла об экономических специальностях.
Решение таких задач связано со знанием некоторых специфических математических моделей из области экономики, умением переводить сформулированные в виде текста условия в уравнения и неравенства и пониманием того, как решения полученных уравнений и неравенств соотносятся с тем, что написано в условии задачи, – то есть какой смысл имеют полученные результаты.
С чего начать подготовку к решению экономической задачи? Прежде всего, стоит вспомнить основные правила решения текстовых задач вообще (они пригодятся и для решения более простой текстовой задачи № 11 варианта КИМ).
Решение любой текстовой задачи складывается из нескольких основных моментов:
• чтение условия задачи; читайте его до тех пор, покуда сможете, не подглядывая в текст, объяснять суть описанного в задаче процесса (без конкретных числовых данных, конечно, – зазубривать ничего не нужно);
• выбор переменных; для каждого типа задач существуют рекомендации, какие величины лучше всего обозначать как переменные (и это не всегда те величины, о которых идет речь в вопросе задачи); переменных при решении текстовой задачи нужно вводить столько, сколько их нужно для того, чтобы просто и логично составить уравнения и неравенства (не бойтесь, если переменных оказалось слишком много – например, больше, чем число уравнений: если вы все делаете правильно, то «лишние» переменные взаимно уничтожатся или сократятся;еще один вариант – в процессе решения надо будет найти не сами переменные по отдельности, а какую-либо их комбинацию);
• составление уравнений и неравенств, формализация того, что необходимо найти в процессе решения задачи; при составлении уравнений обращайте внимание на единицы измерения – они должны быть одинаковыми для всех одноименных величин;
• решение полученного уравнения, неравенства или системы;
• исследование полученного результата и нахождение ответа на вопрос задачи.
Рекомендуем вам «держать в голове» эти основные шаги решения текстовой задачи.
Если все эти правила вам хорошо знакомы и текстовые задачи вы решаете, в принципе, неплохо, то есть умеете составлять математические модели словесно описанных процессов, то дальше нужно выяснить, насколько хорошо вы владеете таким понятием как «процент». Для этого можно решить следующую устную задачку: «Цена на товар была повышена на 25%. На сколько процентов надо теперь ее снизить, чтобы получить первоначальную цену?»
«Очевидный» (и неправильный) ответ – на столько же, хотя на самом деле снизить надо на 20%. Если вы не смогли объяснить себе, почему это так, то надо хорошенько разобраться, что же такое процент. Для этого можно использовать видеоматериалы, тренажеры и задачи для самостоятельного решения, которые есть на сайте «1С:Репетитор». Начать надо с темы «Вычисление “простых” процентов».
Если приведенная выше задачка не загнала вас в тупик, то, немного потренировавшись в вычислении «простых» процентов, можно переходить к освоению формулы «сложных процентов» и ее применению в задачах с экономическим содержанием. Следующий этап – решение задач на банковские вклады, ведь такие задачи уже можно встретить в вариантах КИМ ЕГЭ. Например: «Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на х млн рублей, где х — целое число. Найдите наименьшее значение х, при котором банк за четыре года начислит на вклад больше 7 млн. рублей». (Ответ: 8.)
Сравнительно недавно в вариантах КИМ появились задачи, темой которых являются банковские кредиты. Для решения таких задач необходимо познакомиться с двумя математическими моделями, лежащими в основе наиболее распространенных схем выплат по банковскому кредиту, – дифференцированной и аннуитетной. В основе этих схем лежит уже известная нам формула «сложных» процентов, а также свойства арифметической и геометрической прогрессий. Поэтому прежде чем начинать знакомиться с «кредитной» математикой необходимо повторить некоторые свойства уже упомянутых прогрессий – вам понадобятся определения, формулы n-го члена и суммы n последовательных членов каждой из прогрессий.
При решении задач, в которых речь идет о выплате кредита в соответствии с дифференцированной или аннуитетной схемой, можно действовать двумя способами: либо использовать готовые формулы, полученные в ходе построения соответствующей математической модели, либо вычислять размер очередного платежа пошагово. Выбор способа зависит от условия задачи. Конечно, есть и еще некоторые хитрости в построении решения, которые надо знать.
К наиболее сложным задачам с экономическим содержанием относятся так называемые «задачи на оптимизацию» или экстремальные задачи. Эти задачи описывают разнообразные ситуации, с которыми граждане, предприятия и компании могут встретиться в своей экономической деятельности. К решению таких задач есть несколько подходов, из которых наиболее часто используются метод перебора вариантов и логических рассуждений и исследование функций элементарными методами и с помощью производной.
Как правило, при решении данных задач необходимо либо провести непосредственные вычисления и сравнить их результаты, либо составить уравнение (систему уравнений) и решить его (ее) с учетом некоторых дополнительных условий (например, в целых числах), либо построить функцию, устанавливающую связь между двумя экономическими величинами (например, между объемом производства и прибылью компании), и исследовать ее на экстремальное значение с помощью производной, опять же с учетом того, что данная функций описывает некий реальный процесс, от чего могут зависеть какие-то ограничения на область определения или область значений.
Сложность таких задач в том, что здесь нет готовых методов решения, каждая задача уникальна и требует своего подхода. Поэтому посоветовать можно только одно: чтобы научиться решать такие задачи, надо их решать. Впрочем, этот совет – универсальный.
Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.
Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.
Решение задачи
По условию задачи, фонд продаст все акции и вложит деньги в банк в конце 21-го года, а в конце 25-го года получит максимальную прибыль. Следовательно, в конце 21-го года у фонда будет 2 1 2 = 441 тыс. рублей; эти деньги положат в банк, где в течение 4 лет они будут «расти» по закону «сложных процентов», то есть к концу 25-го года сумма на счете составит 441 r 4 рублей.
Исследуем эту функцию на экстремум с помощью производной:
Поскольку максимальная прибыль фонда будет достигнута, если фонд продаст все акции в конце 21-го года,
f 21 > f 20 f 21 > f ( 22 ) ⇔ 441 r 4 > 400 r 5 441 r 4 > 484 r 3 ⇔ r ∊ 484 441 ; 441 400
Регулярно тренируйтесь в решении задач
Чтобы начать заниматься на портале «1С:Репетитор», достаточно Зарегистрироваться.
Вы можете:
Как решать экономические задачи егэ по математике профильный уровень
За задание №17 по математике ЕГЭ профильный уровень можно получить 3 балла. Мы рассмотрим как решать экономические задачи ЕГЭ по математике, которые в каждом варианте профильного уровня по математике идут под номером 17.
Решение №17 включает в себя обязательное построение математической модели, то есть это обычная текстовая задача, но с экономическим (финансовым) уклоном и чаще всего с большим количеством вычислений.
Можно выделить несколько блоков заданий:
1. Вклады и кредиты
2. Акции и другие ценные бумаги
3. Методы оптимальных решений
Рассмотрим каждый из вышеперечисленных блоков.
Вклады и кредиты
Вклады и кредиты – самый обширный блок. Здесь вы можете встретить различные схемы возврата кредита или увеличения суммы вклада, и ваша задача – упорядочить данные таким образом, чтобы большой массив текста превратился в удобную математическую схему.
Чтобы правильно решать такие задачи, необходимо владеть формулой сложных процентов. Начисление по этой формуле предполагает, что каждый последующий год процент начисляется не на исходную сумму, а на исходную сумму, увеличенную предыдущим начислением процентов.
Формула выглядит следующим образом:
где FV – будущая сумма.
p – процент, в соответствии с которым происходит начисление
n – количество лет начисления процента.
Если начисления происходят не ежегодно, а чаще, например, ежеквартально, формула модифицируется в следующий вид:
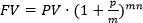
p – процент, в соответствии с которым происходит начисление
n – количество лет начисления процента
m – количество начислений в год (например, m=4, если начисления ежеквартальные).
Давайте отработаем эту формулу на подготовительной задаче.
Задача 1
Алексей положил 100 000 рублей в банк под 6% годовых на 3 года. Какая сумма будет у Алексея через год? Через 2 года? Через 3 года?
Решение:
Рассчитаем по формуле сложного процента сумму через год:
Теперь сумму через 2 года:
Теперь сумму через 3 года:
Более того, вам придётся работать со схемами кредитов/вкладов, поэтому решим более сложную задачу, в которой нужно будет переводить текст в таблицы и уравнения /неравенства.
Задача 2
Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего года и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 28 млн рублей.
Решение:
Пусть искомая сумма составит a млн рублей.
Составим таблицу, чтобы упорядочить данные и построить математическую модель.
По условию, нужно найти наименьшее целое x, для которого выполнено неравенство
a ≥
Наименьшее целое число, при котором знак неравенства выполняется, это число 6.
Значит, искомая сумма — 6 млн рублей.
Ответ: 6 млн рублей.
Акции и другие ценные бумаги
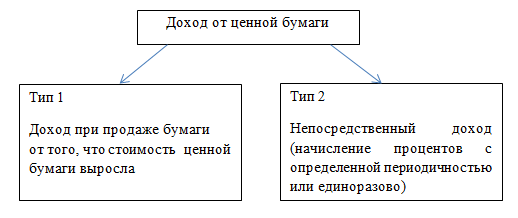
Следующий блок, который мы рассмотрим, затрагивает относительно новое понятие ценной бумаги. Что вам нужно знать о ценной бумаге, чтобы решать подобные задания, не вдаваясь в экономические особенности, это то, как она может приносить доход.
Тип 1: когда вы получаете доход от того, что ценная бумага, которую вы купили ранее, растет в цене. Например, сначала ценная бумага стоила 3 000, а через год стала стоить 4 000. Непосредственно этих 4 000 у вас нет, но вы можете продать ценную бумагу за 4 000 и получите больше, чем потратили за год до этого.
Тип 2: когда вы получаете некий процент от прибыли компании за то, что ранее приобрели ценную бумагу этой компании. Если вы являетесь владельцем акции, то доход данного типа вы получаете в форме дивидендов.
Помимо этого дохода вы также можете продать эту ценную бумагу и, если она теперь стоит больше, чем когда вы ее покупали, вы также получите прибыль. Это не все пути получения дохода от ценных бумаг, но других особенностей вам знать не нужно. При необходимости все дополнительные условия будут описаны в самой задаче.
Рассмотрим следующую задачу, в которой как раз фигурирует понятие ценной бумаги.
Задача 3.
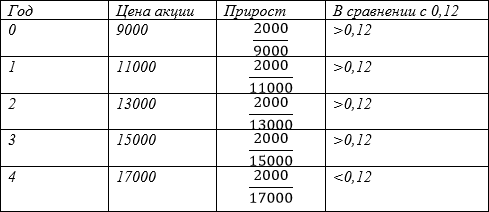
Григорий приобрёл ценную бумагу компании за 9000 рублей в начале 2016 года. Компания находится на стадии активного роста, поэтому цена данной бумаги каждый год возрастает на 2000 рублей. В любой момент Григорий может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 12 %. В начале какого года Григорий должен продать ценную бумагу, чтобы через 15 лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
Решение:
Продать бумагу нужно тогда, когда прирост стоимости ценной бумаги станет меньше, чем банковский процент. Пусть это случится в год n.
К этому моменту n к изначальной цене акции 9000 прибавится n раз по 2000, тогда на текущий момент её цена составит:
Чтобы получить прирост, который Григорий получит, если хранить деньги в форме акции, необходимо ежегодный прирост (в данной задаче – 2000 рублей) поделить на накопленную к данному моменту сумму.
Прирост денежной суммы в банке всегда одинаков и равен предложенному проценту, то есть 0,12.
Либо можем составить уравнение, которое объединит все строчки нашей таблицы:
По прошествии четырёх лет Григорий должен продать бумагу, то есть в начале 2020 года.
Методы оптимальных решений
Это особый блок, позволяющий максимизировать одну целевую функцию при учёте данных в условии ограничений.
Основные типы заданий в этом блоке:
1. Оптимизация работы на производстве с учётом цен на рынке товара и факторов производства;
2. Многозаводское производство (включая разные заводы/ отели/ другие рабочие пространства);
3. Транспортная задача.
Разберём несколько задач с основными методами решения.
Задача.
У фермера есть 2 поля, площадь каждого из которых составляет 10 гектаров. На каждом поле можно выращивать пшеницу и ячмень. Урожайность пшеницы на первом поле составляет 500 ц/га, а на втором поле – 300 ц/га. Урожайность ячменя, наоборот, на первом поле составляет 300 ц/га, а на втором поле – 500 ц/га. При этом известно, что между данными злаками поля можно делить в любом соотношении.
Если известно, что на рынке установилась цена на пшеницу 7000 рублей за центнер, а цена на ячмень 9000 рублей за центнер, то какой наибольший доход фермер может получить?
Решение:
Имеем 2 поля с различными характеристиками.
В целом, продавать ячмень выгоднее, чем продавать пшеницу, так как 9000 > 7000 рублей.
Более того, известно, что на втором поле урожайность ячменя выше, чем урожайность пшеницы (500 ц/га против 300 ц/га). Тогда очевидно, что второе поле полностью фермер займёт ячменём, откуда получит:
10·500· 9000= 45000000 рублей
Ситуация с первым полем не так очевидна.
Продавать ячмень, как и прежде, выгоднее, чем продавать пшеницу. Однако на первом поле урожайность ячменя ниже, чем урожайность пшеницы (300 ц/га против 500 ц/га).
Поэтому необходимо сравнить соотношения этих величин:
Тогда получается, что засеять первое поле пшеницей выгоднее, так как низкая цена компенсируется высокой урожайностью.
Доход с первого поля:
10 · 500 ·7000 = 35000000 рублей
Суммарный доход составит:
35000000 рублей + 45000000 рублей = 80000000 рублей
Ответ: 80000000 рублей
Есть и другие типы заданий, в которых необходимо будет применить не житейские знания, а навыки составления уравнений и нахождения наименьшего/ наибольшего значений функций.
Задача.
На двух заводах есть по 360 рабочих, каждый из которых готов трудиться по 5 часов в сутки для обработки чёрных или цветных металлов. На первом заводе один рабочий за час обрабатывает 0,3 кг чёрных металлов или 0,1 кг цветных металлов. На втором заводе для обработки x кг чёрных металлов в день требуется x2 человеко-часов труда, а для обработки у кг цветных металлов в день требуется у2 человеко-часов труда.
Владельцу заводов поступил заказ на обработку металлов, причём 1 кг чёрных металлов ценится заказчиком так же, как 1 кг цветных металлов. Какую наибольшую массу обработанных металлов может за сутки суммарно получить заказчик?
Решение:
Как и дано в условии, 1 кг чёрных металлов ценится заказчиком так же, как 1 кг цветных металлов, что означает, что металлы взаимозаменяемы в пропорции 1:1.
Пусть на втором заводе t рабочих обрабатывают чёрные металлы, тогда (360-t) рабочих обрабатывают цветные металлы.
Знаем, что x2 человеко-часов труда требуется обработки x кг чёрных металлов, а у2 человеко-часов труда требуется в день для обработки у кг цветных металлов.
На первом заводе один рабочий за час обрабатывает 0,3 кг чёрных металлов или 0,1 кг цветных металлов, однако чёрные и цветные металлы для заказчика равнозначны, из чего сделаем вывод, что все 360 рабочих обрабатывают чёрные металлы, то есть 108*5 = 540 кг в день.
Имея соотношение на втором заводе и производительность рабочих на первом заводе, составим функцию возможного количества обработанных металлов:
Необходимо найти наибольшее значение этой функций. Последовательность действий мы уже знаем из темы «Анализ функций». Необходимо:
1. Найти производную функции;
2. Приравнять производную к 0, получить точки, подозрительные на экстремум;
3. Определить знаки производной на полученных промежутках и проверить, какие точки являются точкой максимума, а какие – точкой минимума.
Проведём такую последовательность действий с нашей производственной функцией.
Видим, что экономическая задача достаточно разнообразна, но и решать вы её можете абсолютно разными способами – через производные, составление таблиц, схем, выведение формул и простой перебор вариантов.
Самое главное – внимательно прочитать и понять условие.
Примеры решения задач
Задача 1. В 2019 году клиент планирует открыть вклад в банке 1 ноября сроком на 1 месяц под 11% годовых. Какая сумма денег окажется на счёте вклада 1 декабря того же года, если планируемая сумма вклада равна 100 000 рублей? Ответ округлите до двух знаков после запятой.
Решение: При однократном начислении процентов через дней на вклад под годовых в невисокосный год получим сумму
Число в скобках с точностью до 7 знаков после запятой равно 1,0090411, значит, S=100 904,11Таким образом, на счёте вклада будет 100 904 рубля 11 копеек.
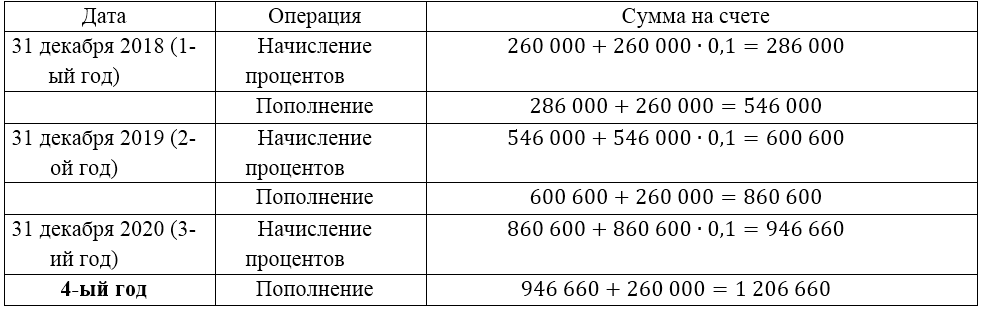
Задача 2. Через сколько полных лет у клиента на счету будет не менее 950 000 рублей, если он намерен открыть вклад 31 декабря и планирует каждый год класть на счет 260 000 рублей при условии, что банк раз в год (начиная со следующего года) 31 декабря будет начислять 10% на имеющуюся сумму?
Решение:
Будем последовательно вычислять сумму на счете и упорядочивать данные с помощью таблицы.
Задача 3. По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» увеличивает эту сумму на 11% в течение каждого из первых двух лет, а на третий год начисляемые проценты изменяются. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором по истечении трёх лет этот вклад всё ещё будет выгоднее вклада «А».
Решение:
Пусть на каждый тип вклада была внесена сумма По вкладу «А» сумма каждый год увеличивается на
умножается на коэффициент 1,1.
Тогда по вкладу «А» после первого года сумма станет равна ;
после второго года: 1,21S;
после третьего года: 1,331S.
По вкладу «Б» после первого года сумма станет равна1,11S;
после второго года 1,2321S.
Пусть на третий год по вкладу «Б» банк увеличивает сумму на r%. Тогда после третьего года по вкладу «Б» сумма станет равна
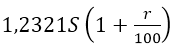
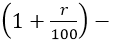
По условию требуется найти наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А», то есть сумма через три года на вкладе «Б» должна быть больше суммы на вкладе «А». Составим неравенство:
Так как r— натуральное число, то наименьший процент равен 9%.
Задача 4. Сергей планирует приобрести ценную бумагу за 7 тысяч рублей. Цена бумаги каждый год будет возрастать на 2 тысячи рублей. В любой момент Сергей сможет продать ценную бумагу и вырученные деньги положить на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В течение какого года после покупки Сергей должен продать ценную бумагу, чтобы через 30 лет после покупки этой бумаги сумма на счете стала наибольшей?
Решение.
Во второй год цена ценной бумаги составит: (7+2) тысячи рублей
В третий год (7+2)+2= 7+2∙2 тысячи рублей
В четвертый год (7+2)+2)+2= 7+2∙3 тысячи рублей
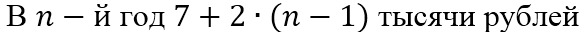
Сопоставим 10% банковский рост цены бумаги ее ежегодному росту на 2000 рублей.
10% от цены бумаги на
Ценную бумагу стоит продать тогда, когда 10% от цены бумаги станут больше, чем 2 тысячи рублей.
Наименьшее натуральное n, удовлетворяющее этому неравенству, равно 8.
Задача 5.
Пенсионный фонд владеет ценными бумагами, которые стоят t 2 тыс. рублей в конце года t (t=1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 20%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце тридцатого года сумма на его счёте была наибольшей?