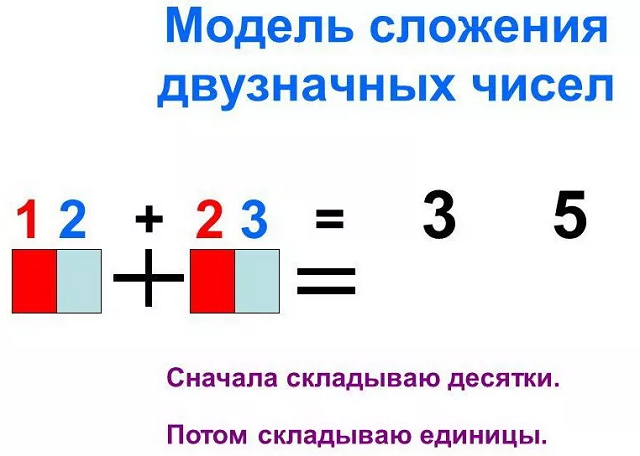
Как решать двузначные примеры
Как научить ребёнка двузначным числам

Главное правило: действуем последовательно. Переходить к значениям больше 10 стоит только после того, как ребёнок наверняка освоил математические примеры до этого числа.
Было 10 — стало 1. Как это?
У учителей математики есть очень простой и наглядный способ превращения 10 палочек в 1 десяток. Всё просто: их нужно посчитать, чтобы было ровно 10, и связать нитью. Теперь это уже не кучка разрозненных предметов, а цельный пучок. Главное, что он 1.
Продолжаем вязать пучки дальше. Пусть ученик увидит 2 и больше связок по 10 палочек.
Что такое «дцать»?
Расскажите ребёнку, что слово «дцать» — очень древнее, и оно означает «десять». Теперь можно двигаться дальше. Разбираем с учеником значения чисел второго десятка:
Продолжаем в том же духе до 20. Некоторое время нужно посвятить тому, чтобы ребёнок закрепил полученные знания. На этом этапе нужно решать с ним простые примеры на сложение и вычитание. Продолжаем использовать разные предметы для наглядности: яблоки, игрушки, ложки и так далее.
Например, разложим перед ребёнком 12 карандашей. Пусть он сам сформирует связку из 10 штук и закрепит верёвкой. Теперь добавляем ещё 3 карандаша. Малыш должен увидеть, что связанные карандаши мы не трогаем, а к 2 свободным карандашам добавляем ещё 3. Получается, у нас есть 1 связка и ещё 5 карандашей, то есть 15. Таким же способом представляем простые примеры на вычитание.
При регулярных занятиях наглядные примеры очень скоро утратят свою актуальность, и ребёнок научится считать в уме.
Как зовут десятки?
Теперь малышу следует познакомиться с круглыми значениями более подробно. «Двадцать» и «тридцать» он уже воспримет легко. Стоит подробнее остановиться на цифре «сорок» и рассказать, что её название отличается от других, но означает оно 4 десятка.
Ученику предстоит усвоить ещё одно окончание — «десят», что также означает «десять». Расскажите, что названия чисел от 50 до 80 формируются одинаково, то есть сначала идёт количество десятков, а затем приставка «десят», например, «восемь-десят».
Ещё одно нестандартное название —«девяносто», то есть «9 десятков».
Закрепляем знания при помощи кубиков

Итак, имеем 4 ряда. Можно просто пересчитать все кубики. Затем стоит посчитать, сколько всего зелёных и сколько жёлтых кубиков. И напоследок, считаем зелёные кубики десятками, а жёлтые — единицами. То есть у нас 2 ряда зелёных кубиков — это 2 десятка, а жёлтых кубиков — 4 + 3 = 7. Получаем 27.
Считаем на палочках из-под мороженого
Вы любите мороженое на палочке? Прекрасно. Это поможет вашему малышу разобраться с двухразрядными значениями. Чтобы лето прошло не даром, соберите коллекцию палочек из-под мороженого. Максимальное количество — 20 штук. Теперь на одной стороне каждой палочки рисуем 5 точек слева и 5 точек справа. Переворачиваем все палочки и рисуем на каждой по 1 точке в центре.
Два участника берут по 10 штук и бросают на пол. Палочки, на которых мы видим 10 точек, — это десятки, а с одной точкой посередине — это единицы. Сортируем их на 2 группы. Называем число, которое вышло у каждого игрока.
Выиграл тот, у кого значение больше. Смысл занятия — показать наглядно, что числа могут состоять из двух разрядов, и научиться оперировать ими.
Таблица двузначных чисел
Когда ребёнок уже немного освоился, сделайте таблицу значений от 1 до 100. Первый ряд — от 1 до 10, второй — от 11 до 20, самый последний — от 91 до 100. Вырежьте из картона 10 полосок, которые соответствуют длине и ширине одного рядочка. Также вырежьте 10 квадратиков, которые соответствуют размерам одной ячейки таблицы.
Теперь назовите ученику любое число больше 10, например, 35. Он должен взять 3 длинные полоски и закрыть ими 3 верхних ряда таблицы. Затем при помощи 5 квадратиков закрываем цифры 31, 33, 34 и 35.
Считаем с переходом через десяток
Как объяснить ребёнку принцип сложения с переходом через десяток? Сейчас всё подробно обсудим. Рассмотрим пример 17 + 5:
Согласитесь — это непростой алгоритм для маленького ученика. Поэтому не расстраивайтесь, если он не поймёт сразу всё. Разберите подобный пример на любых предметах. В конце концов малыш сможет разобраться.
Как научить ребёнка числам с двумя разрядами и не сойти с ума?
Будьте добрым и очень терпеливым учителем. А мы дадим несколько полезных советов:
Все дети развиваются в индивидуальном темпе. Некоторые владеют двухразрядными числами ещё до школы, а у других они вызывают затруднение и во 2 классе. Будьте терпеливы и занимайтесь систематично, но понемногу. Мы уверены, что у вас всё получится! Будьте с нами на связи и привлекайте к обсуждению своих знакомых. До новых встреч!
Расскажите о нем свои знакомым, нажав на одну из кнопок соц. сетей:
Как научить ребёнка считать в уме двузначные числа во 2 классе
Взрослому человеку не стоит объяснять насколько важно уметь считать в уме. Конечно, в повседневной жизни нам не надо за считанные секунды перемножать друг на друга семизначных «монстров». Обычно большинству людей хватает умения быстро складывать и перемножать числа значительно меньших значений. Но чтобы оперировать в уме даже ими, важно ещё в школьном возрасте развить в детях этот навык. А как научить ребёнка считать в уме двузначные числа второкласснику, если в школе этому не уделяется большого внимания? Достаточно просто. Конечно, придётся потратить на это некоторое количество времени, сил и нервов, но зато это позволит избежать многих проблем в будущем. Причём и маленькому человеку, и его родителям.
Сразу стоит оговориться, что в дальнейшем речь пойдёт об умении складывать и вычитать в уме двузначные числа, т.к. умножение, согласно современным школьным программам, детки начинают проходить только в конце второго класса.
И ещё: формулы в примерах приведены исключительно для понимания взрослыми сути методики. Второклассникам их показывать стоит только в том случае, если они неплохо справляются с решением подобных задачек в своих тетрадях. В противном случае они могут просто запутаться в числах. А в случае крайней необходимости для наглядности можно воспользоваться, к примеру, счётными палочками.
С чего начать обучение счету в уме для второклассника
Сразу стоит сказать, что приступать к выработке умения считать в уме двухзначные числа ребёнку-второкласснику можно только в том случае, если он без труда работает в уме с цифрами от 0 до 9. Если же младший школьник до сих пор использует для подсчётов в пределах 10-18 собственные пальцы, то для начала его следует научить работать с подобными примерами без использования подручных средств.
В том случае, если с однозначными числами ребёнок общается уже на «ты», можно приступать к дальнейшей работе. На этом этапе школьника стоит научить быстро решать примеры с цифрами 7, 8 и 9. Этот навык поможет маленькому математику отработать навык работы с составом числа.
Тут все просто: цифра 7, 8 или 9 раскладывается таким образом, чтобы после прибавки одного кусочка к двузначному числу получилось число круглое, а затем в разряд единиц добавить остаток:
Аналогичная ситуация и с вычитанием:
Иногда педагоги рекомендуют применять методику чуть сложнее. Прибавлять сначала десяток, а потом вычитать из него количество единиц, которых вычитаемому не хватает до 10: 45+7=45+(10-3)=55-3=52. Однако этот способ ребёнку воспринимать сложнее. Лучше его объяснить позднее, когда навык счёта в уме с вышеуказанными тремя цифрами уже будет наработан. Вот тогда для упрощения некоторых вычислений пригодится и данная методика.
После того, как ребёнок освоит решение примеров с двузначными числами и цифрами 7, 8, 9 можно приступать непосредственно к обучению счёта в уме двузначных чисел.
Работа с двузначными числами
На самом деле работа в уме с двузначными (и даже трёхзначными) числами достаточно проста. Здесь применяются те же алгоритмы, что и при решении примеров с цифрами 7, 8, 9. Различия лишь в том, что работать приходится сразу и с единицами, и с десятками.
Сложение двузначных чисел в уме
Ребёнку надо объяснить, что если последние цифры обоих чисел меньше 5 или их сумма меньше или равна 9, то подсчёт сводится к элементарному суммированию единиц и десятков:
21+16=(20+1)+(10+6)=(20+10)+(1+6)=30+7=37.
Если же последние цифры больше 5 или их сумма больше 9, то можно применить одну из двух методик счёта, в основе которых лежит опять же разложение числа по составу.
В первом случае следует поступить так же, как и в вариантах с цифрами 7, 8, 9. Округлить первое слагаемое за счёт «разбора на кусочки» единиц второго слагаемого, а затем суммировать полученные числа:
Во втором – округлить второе слагаемое до круглого числа, произвести суммирование и вычесть лишний кусочек:
Вычитание двузначных чисел в уме
Второклассники, которые освоили сложение двухзначных чисел в уме, без труда осваивают и обратное действие – вычитание, поскольку применяются тут аналогичные алгоритмы.
В простых случаях десятки вычитаются из десятков, а единицы из единиц:
В более сложных случаях лучше применять метод округления:
А в чём же методика
Всё вышеописанное выглядит достаточно простым. Это и в самом деле так. Но просто это выглядит для родителей, которые учились значительно больше, чем два класса. Так что суть методик не столько в том, какие действия нужно делать в уме, сколько в поэтапном грамотном объяснении и отработке навыков путём постоянных тренировок.
Работать с ребёнком нужно регулярно. Объяснив один из алгоритмов в течение некоторого времени нужно закреплять навык, доводя его до автоматизма. Сильно мучить второклассника при этом не следует. Достаточно заниматься 10-15 минут в день, а если ребёнок хорошо справляется с заданиями, то хватит и 3-4 примеров. Но даже в последнем случае останавливаться на достигнутом не стоит. Если прекратить тренироваться, то алгоритмы могут забыться, а навык пропасть.
Занятия можно проводить по дороге в школу или из неё. Благо каких-то инструментов для этого не нужно. А можно делать это и дома, в форме игры, например: «В магазин». Можно играть и в развивающие счётные способности настольные игры типа математического лото.
Неплохим подспорьем в современном мире, где правят удалённые технологии, может стать и множество специально разработанных приложений для обучения быстрому счёту в уме, а также онлайн игры и сервисы. Кстати, в этом случае тоже нужно следить, чтобы младший школьник не слишком долго сидел, уткнувшись в телефон или монитор компьютера. Пятнадцати минут в день – вполне достаточно.
Поведение родителей
Чтобы ребёнок быстро освоил счёт двухзначных чисел в уме, родители должны создать доброжелательную атмосферу. Даже второклассник всё равно является ещё малышом и с большим удовольствием займётся интересным и весёлым делом, а не скучным образовательным процессом. Именно способствующую обучению атмосферу и должны обеспечить родители.
Кроме того, маме и папе надо запастись терпением, не ругаться, если у чада что-то не получается и, тем более, не заставлять его работать через силу. Пользы от этого точно не будет.
Как решать двузначные примеры
Если вы примените правильные методы и организуете обучение в игровой форме, ребенок быстрее усвоит сложную арифметику.
Бесплатные занятия с логопедом
Обучать ребенка арифметике довольно непросто, ведь она состоит из трёх этапов. Для начала придется разобраться с числами от 0 до 9, а потом со всем остальным. Однако и с двузначными числами нужно работать поэтапно. Пусть ребенок отработает действия с числами от 10 до 20, затем от 20 до 30 и так далее. Если вы примените правильные методы и организуете обучение в игровой форме, ребенок быстрее усвоит сложную арифметику.
Итак, обучение проходит в несколько этапов.
Подготовка
На этом этапе ребенок учится складывать и вычитать двузначные числа. Пусть ребенок сначала поработает с круглыми числами (научится их складывать и вычитать). После научите его выделять в числах разрядные слагаемые (34=30+4). Попробуйте объяснить ему, что в числе 34 получится 3 десятка и 4 единицы. Справиться с этим вам помогут счетные палочки. Это довольно практичный метод, который применяется в школах уже давно.
Примите к сведению, что счетные палочки можно легко заменить на детали лего или какой-нибудь конструктор: мелкие детали— это единицы, детали покрупнее— это десятки. Сразу после этого можно переходить к сложению и вычитанию круглых чисел.
Сложение и вычитание круглых чисел
Существуют разные способы обучения ребенка сложению и вычитанию круглых чисел.
По такому же принципу разберите и вычитание круглых чисел. Как только малыш усвоит эти несложные манипуляции, можно двигаться дальше.
Складываем и вычитаем числа без перехода через разряд
Чтобы разобраться с этим этапом, придётся объяснять действия на практике. Скажем, нужно выполнить следующее действие: 24+31. Тут уж нам придется изучить ещё 1 способ сложения/вычитания. Выкладываем палочки по горизонтальной линии — это будут наши десятки; а вертикально выложенные палочки— это единицы. Теперь складываете вертикальные палочки с вертикальными, а горизонтальные с горизонтальными. Так выкладываем 2 палочки горизонтально и 4 вертикально, а рядом— 3 горизонтальные и 1 вертикальную палочку. Сложив их, получаем 5 горизонтальных палочек и 5 вертикальных, то есть, окончательный ответ 55. Постепенно ребёнок усвоит, что единицы нужно добавлять к единицам, а к десяткам добавляются десятки.
Следующее, что вы можете разобрать с малышом— это научиться складывать и вычитать в столбик. Здесь необходимо объяснить будущему школьнику, что единицы записываются под единицами, а десятки под десятками. Возможно, будет полезно вначале разложить кусочки лего и найти результат, а потом провести расчет в столбик.
Таким же образом можно разобрать и вычитание ( с помощью палочек, кусочков Лего и записи в столбик). Если ребенок освоил технику со сложением, ему будет не трудно справиться и с вычитанием.
Сложение и вычитание чисел с переходом через разряд
Сложность выполнения сложения и вычитания чисел через разряд заключается в том, что тут придётся «занимать» и «запоминать» числа.
Попробуем решить такой пример (26+35) с помощью палочек.
Как только этот этап пройден, можно рассмотреть и другие варианты сложения двузначных чисел.
Вычитание тоже покажите на наглядном примере. Допустим, 53-27.
Завершив наглядный метод, начните считать и другими способами:
Чтобы объяснить ребёнку тонкости арифметических действий, возьмите в помощь счёты. Это удобно и практично. А ещё ребёнок мог бы записать числа на них и практиковаться, пока не дойдёт до автоматизма.
Помните, что каждый ребёнок индивидуален и выбирать способ обучения необходимо исходя из особенностей ребенка. Кому-то легко дается счет на палочках, кто-то предпочитает считать в столбик. А кому-то для практики требуются месяца, ребёнок считает разными способами, но ему так и не удаётся научиться считать быстро и без ошибок. Родителям стоит быть терпеливыми, помогать малышу, решать примеры вместе и не злиться. Пусть он чувствует вашу поддержку и заботу. А с регулярной практикой у малыша обязательно все получится.
Как объяснить ребенку сложение и вычитание двухзначных чисел
Обучать ребенка арифметике довольно непросто, ведь она состоит из трёх этапов. Для начала придется разобраться с числами от 0 до 9, а потом со всем остальным. Однако и с двузначными числами нужно работать поэтапно. Пусть ребенок отработает действия с числами от 10 до 20, затем от 20 до 30 и так далее. Если вы примените правильные методы и организуете обучение в игровой форме, ребенок быстрее усвоит сложную арифметику.
Итак, обучение проходит в несколько этапов.
Подготовка
На этом этапе ребенок учится складывать и вычитать двузначные числа. Пусть ребенок сначала поработает с круглыми числами (научится их складывать и вычитать). После научите его выделять в числах разрядные слагаемые (34=30+4). Попробуйте объяснить ему, что в числе 34 получится 3 десятка и 4 единицы. Справиться с этим вам помогут счетные палочки. Это довольно практичный метод, который применяется в школах уже давно.
Примите к сведению, что счетные палочки можно легко заменить на детали лего или какой-нибудь конструктор: мелкие детали— это единицы, детали покрупнее— это десятки. Сразу после этого можно переходить к сложению и вычитанию круглых чисел.
Сложение и вычитание круглых чисел
Существуют разные способы обучения ребенка сложению и вычитанию круглых чисел.
По такому же принципу разберите и вычитание круглых чисел. Как только малыш усвоит эти несложные манипуляции, можно двигаться дальше.
Складываем и вычитаем числа без перехода через разряд
Чтобы разобраться с этим этапом, придётся объяснять действия на практике. Скажем, нужно выполнить следующее действие: 24+31. Тут уж нам придется изучить ещё 1 способ сложения/вычитания. Выкладываем палочки по горизонтальной линии — это будут наши десятки; а вертикально выложенные палочки— это единицы. Теперь складываете вертикальные палочки с вертикальными, а горизонтальные с горизонтальными. Так выкладываем 2 палочки горизонтально и 4 вертикально, а рядом— 3 горизонтальные и 1 вертикальную палочку. Сложив их, получаем 5 горизонтальных палочек и 5 вертикальных, то есть, окончательный ответ 55. Постепенно ребёнок усвоит, что единицы нужно добавлять к единицам, а к десяткам добавляются десятки.
Следующее, что вы можете разобрать с малышом— это научиться складывать и вычитать в столбик. Здесь необходимо объяснить будущему школьнику, что единицы записываются под единицами, а десятки под десятками. Возможно, будет полезно вначале разложить кусочки лего и найти результат, а потом провести расчет в столбик.
Таким же образом можно разобрать и вычитание ( с помощью палочек, кусочков Лего и записи в столбик). Если ребенок освоил технику со сложением, ему будет не трудно справиться и с вычитанием.
Сложение и вычитание чисел с переходом через разряд
Сложность выполнения сложения и вычитания чисел через разряд заключается в том, что тут придётся «занимать» и «запоминать» числа.
Попробуем решить такой пример (26+35) с помощью палочек.
Как только этот этап пройден, можно рассмотреть и другие варианты сложения двузначных чисел.
Вычитание тоже покажите на наглядном примере. Допустим, 53-27.
Завершив наглядный метод, начните считать и другими способами:
Чтобы объяснить ребёнку тонкости арифметических действий, возьмите в помощь счёты. Это удобно и практично. А ещё ребёнок мог бы записать числа на них и практиковаться, пока не дойдёт до автоматизма.
Помните, что каждый ребёнок индивидуален и выбирать способ обучения необходимо исходя из особенностей ребенка. Кому-то легко дается счет на палочках, кто-то предпочитает считать в столбик. А кому-то для практики требуются месяца, ребёнок считает разными способами, но ему так и не удаётся научиться считать быстро и без ошибок. Родителям стоит быть терпеливыми, помогать малышу, решать примеры вместе и не злиться. Пусть он чувствует вашу поддержку и заботу. А с регулярной практикой у малыша обязательно все получится.
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
На уроке научимся делить столбиком на двузначное число без остатка и с остатком, повторим единицы массы, будем решать задачи.
Ребята, делить столбиком на двузначное число совсем непросто! Потребуется серьезная разминка. Проверим, кто из вас отлично знает таблицу умножения и деления. Решите примеры устно, найдите ответ и соответствующую ему букву. Запишите числа в таблицу в порядке возрастания. Какое слово получилось? Прочитайте.
Правильный ответ найдете в рубрике «Это интересно!».
Письменное деление на двузначное число
Что нужно знать и уметь, чтобы хорошо научиться делить на двузначное число? Подумайте, ребята!
Конечно, надо знать назубок таблицу умножения – это первое. А второе – уметь делить на однозначное число столбиком (уголком).
Давайте вспомним алгоритм деления на однозначное число.
Решите самостоятельно примеры уголком и проверьте себя по образцу.
А теперь рассмотрим деление уголком на двузначное число. Нам понадобится черновик. При делении на двузначное число цифру, которую мы подобрали, требуется проверить умножением. Если цифра не подошла (а такое бывает), подбираем следующую цифру, снова проверяем умножением и так далее. Все эти вычисления лучше выполнить на черновике. Например, разделим 624 на 26. Запишем пример столбиком (уголком).
Обязательно проговариваем каждый этап вычислений.
Пользуясь алгоритмом, решите самостоятельно два примера столбиком. Проговаривайте каждый этап, чтобы не допустить ошибку. Сравните с образцом.
448 : 64 952 : 34
Ребята, вы заметили, что алгоритм остается прежним? Требуется лишь больше внимания и сосредоточенности.
Попробуйте и вы, ребята, овладеть делением!
Деление на двузначное число с остатком
Действует ли при делении с остатком какой-либо другой алгоритм? Нет! При делении с остатком рассуждают точно так же, как и при делении без остатка.
Ребята, какое правило нужно знать и обязательно проверять при делении с остатком?
А теперь решите самостоятельно примеры на деление с остатком. Не забывайте сравнивать остаток с делителем, сделайте проверку.
272 : 98 495 : 46 385 : 65 321 : 47
Проверь себя.
Ребята, в каком примере вы встретили затруднение? Рассмотрим вместе пример
495 : 46
Почему в частном появился 0 (нуль)?
Первое неполное делимое 49. Делим на 46. Берем по 1. Остаток 3 меньше делителя 46. Делим верно. Сносим следующую цифру 5.
35 делим на 46. Берем по 0 (35 меньше, чем 46). Остаток 35 меньше делителя, разделили верно. Сделаем проверку, убедимся в правильности вычислений.
Уметь делить с остатком – полезный навык, который не раз поможет вам в решении практических задач. Например, для постройки одинаковых башен у вас имеется 430 деталей лего-конструктора. Сколько башен можно построить, если на каждую нужно 35 деталей? Останутся ли лишние детали?
Давайте вместе решим эту задачу.
430 разделим на 35. Сделаем это столбиком (уголком).
Мы видим, что при делении получился остаток 10. Делаем вывод: из 430 деталей лего-конструктора можно сделать 12 одинаковых башен и еще 10 деталей останется.
Разделить можно на черновике, а решение в тетради записать в строчку.
430 : 35 = 12 (ост.10) – башен можно сделать.
Ответ: 12 башен и 10 деталей останется.
Если вы хорошо умеете делить с остатком, решение можно сразу записать в тетрадь:
Решите самостоятельно практическую задачу.
Задача
Ребята 4 класса изготовили для первоклассников 126 закладок в учебники. Сколько закладок достанется каждому первокласснику, если в первом классе 25 учеников? Останутся ли лишние закладки?
Проверь себя.
Решение задач с единицами массы
Ребята, какие единицы массы вы знаете? Давайте вспомним!
Игра
В каждом столбике найди «лишнее» слово, обоснуй свой ответ.
Вспомним таблицу единиц массы.
Задача
В тепличном хозяйстве выращивают огурцы и помидоры. В первой теплице собрали 132 кг огурцов. Во второй теплице собрали 1 ц 56 кг помидоров. Урожай огурцов или помидоров богаче и на сколько килограммов?
Разберем задачу вместе.
Выразим 1 ц 56 кг в килограммах. Из таблицы видим, что 1 ц = 100 кг, значит,
156 – 132 = 14 (кг) – собрали больше помидоров, чем огурцов.
Ответ: на 14 кг больше.
Следующую задачу решите самостоятельно. Проверьте по образцу.
Задача
5 т яблок разложили в ящики по 10 кг в каждый и отправили в хранилище. 120 ящиков с яблоками развезли в магазины города. Сколько килограммов яблок осталось в хранилище.
Проверь себя.
Решение задачи можно записать выражением: (5 000 : 10 – 120) ∙10 = 3 800
А теперь разберем задачу, в которой встретится деление с остатком.
Задача
В хозяйстве собрали 5 ц клубники. 300 кг клубники оставили в ящиках, а остальную клубнику расфасовали в небольшие контейнеры по 300 г. Сколько контейнеров с клубникой получилось? Сколько граммов клубники осталось?
Сначала выразим 5 ц в килограммах.
Узнаем, сколько кг клубники расфасовали в контейнеры.
500 – 300 = 200 (кг) – расфасовали в контейнеры.
Выразим 200 кг в граммах.
Разделим 200 000 на 300 столбиком.
Сделаем вывод: если в условии задачи содержатся разные единицы массы, то необходимо выразить их в одинаковых единицах.
Сегодня на уроке мы научились делить столбиком на двузначные числа с остатком и без остатка, повторили единицы массы, решали задачи.