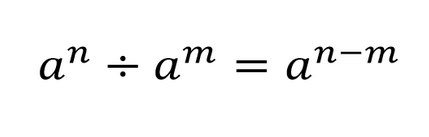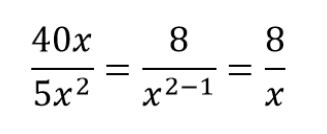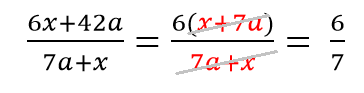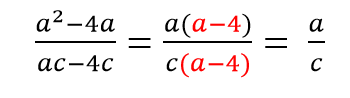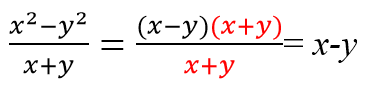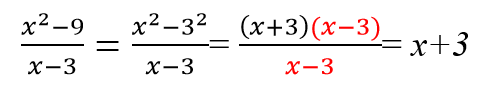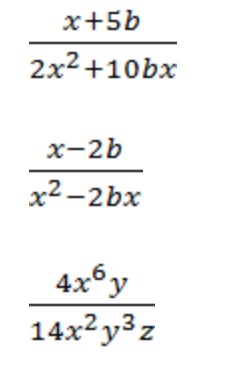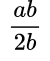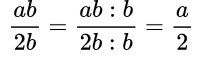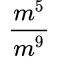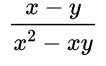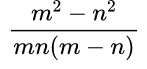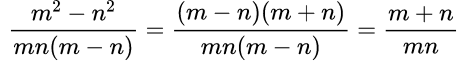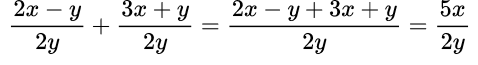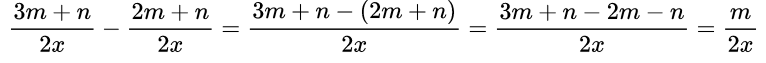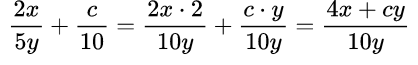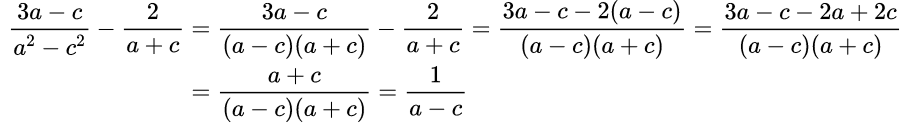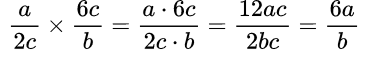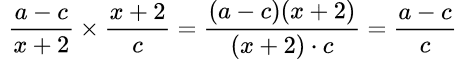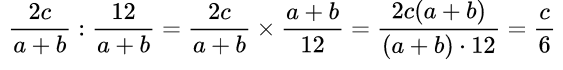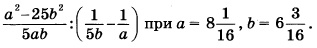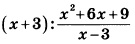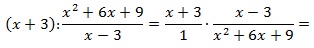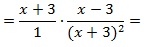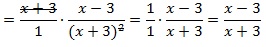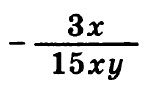Как решать дроби с буквами

Алгебраические дроби. Сокращение алгебраических дробей

Прежде чем перейти к изучению алгебраических дробей рекомендуем вспомнить, как работать с обыкновенными дробями.

Любая дробь, в которой есть буквенный множитель, называется алгебраической дробью.

Примеры алгебраических дробей.

Как и у обыкновенной дроби, в алгебраической дроби есть числитель (наверху) и знаменатель (внизу).

Сокращение алгебраической дроби

Алгебраическую дробь можно сокращать. При сокращении пользуются правилами сокращения обыкновенных дробей.

Напоминаем, что при сокращении обыкновенной дроби мы делили и числитель, и знаменатель на одно и тоже число.

Алгебраическую дробь сокращают таким же образом, но только числитель и знаменатель делят на один и тот же многочлен.

Рассмотрим пример сокращения алгебраической дроби.

Разделим, и числитель, и знаменатель на « a 2 ». При делении одночленов используем свойство степени частного.

Напоминаем, что любая буква или число в нулевой степени — это единица.

Нет необходимости каждый раз подробно записывать, на что сокращали алгебраическую дробь. Достаточно держать в уме степень, на которую сокращали, и записывать только результат.

Краткая запись сокращения алгебраической дроби выглядит следующим образом.

Сокращать можно только одинаковые буквенные множители.

Нельзя сокращать

Можно сокращать

Другие примеры сокращения алгебраических дробей.

Как сократить дробь с многочленами

Рассмотрим другой пример алгебраической дроби. Требуется сократить алгебраическую дробь, у которой в числителе стоит многочлен.

Сокращать многочлен в скобках можно только с точно таким же многочленом в скобках!

Ни в коем случае нельзя сокращать часть многочлена внутри скобок!

Неправильно

Правильно

Определить, где заканчивается многочлен, очень просто. Между многочленами может быть только знак умножения. Весь многочлен находится внутри скобок.

После того, как мы определили многочлены алгебраической дроби, сократим многочлен « (m − n) » в числителе с многочленом « (m − n) » в знаменателе.

Примеры сокращения алгебраических дробей с многочленами.

Вынесение общего множителя при сокращении дробей

Чтобы в алгебраических дробях появились одинаковые многочлены иногда нужно вынести общий множитель за скобки.

В таком виде сократить алгебраическую дробь нельзя, так как многочлен
« (3f + k) » можно сократить только со многочленом « (3f + k) ».

Поэтому, чтобы в числителе получить « (3f + k) », вынесем общий множитель « 5 ».

Сокращение дробей с помощью формул сокращенного умножения

В других примерах для сокращения алгебраических дробей требуется
применение формул сокращенного умножения.

В первоначальном виде сократить алгебраическую дробь нельзя, так как нет одинаковых многочленов.

Но если применить формулу разности квадратов для многочлена « (a 2 − b 2 ) », то одинаковые многочлены появятся.

Другие примеры сокращения алгебраических дробей с помощью формул сокращенного умножения.

Источник

Как сокращать алгебраические дроби?

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение

Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:

Алгебраическая дробь содержит буквенные множители и степени.

Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.

Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.

Сокращение алгебраических дробей

Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.

Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.

Сокращение дробей с буквами и степенями проходит в три этапа:

Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:

Пример сокращения дроби со степенями и буквами:

Получаем сокращенную дробь.

Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.

❌ Так нельзя	✅ Так можно

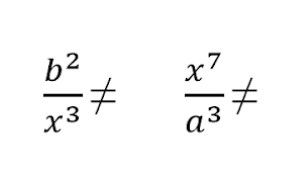Примеры сокращения алгебраических дробей с одночленами:

Пример сокращения №1.

Получаем сокращенную алгебраическую дробь.

Пример сокращения №2.

Получаем сокращенную дробь.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Сокращение алгебраических дробей с многочленами

Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:

Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.

Примеры сокращения алгебраических дробей с многочленами:

Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).

Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.

Вынесение общего множителя при сокращении дробей

При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.

Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:

Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.

Пример 1.

Пример 2.

Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.

Сокращение дробей. Формулы сокращенного умножения

Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.

Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.

Примеры сокращения дробей с помощью формул сокращенного умножения:

Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.

Примеры сокращения дробей за 7 и 8 классы

Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.

Источник

Алгебраические дроби

теория по математике 📈 алгебраические выражения

Любая обыкновенная дробь называется алгебраической дробью, так как она представляет собой деление, записанное с помощью дробной черты. В алгебраической дроби могут встречаться не только числа, но и буквенные выражения.

Примеры алгебраических дробей:

Для алгебраических дробей применяются правила, аналогичные обыкновенным дробям.

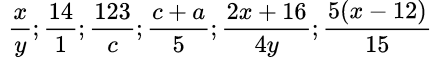
Сокращение алгебраической дроби

Сократить алгебраическую дробь – это значит разделить числитель и знаменатель на одно и то же выражение, на их общий множитель (одночлен, его степень или многочлен) – применяется основное свойство дроби. Причем и числитель, и знаменатель должны содержать множители.

Пример №1. Сократим дробь:

В числителе и знаменателе дроби мы видим переменную b, на которую и разделим каждую часть дроби:

Промежуточные действия можно не записывать, а выполнять устно.

Пример №2. Сократим дробь:

Здесь содержатся степени с одинаковым основанием, поэтому, необходимо помнить еще и правило деления степеней с одинаковым основанием (основание остается прежним, а показатели степеней вычитаем). Сократим дробь на меньшую степень – на m 5 :

Пример №3. Сократим дробь:

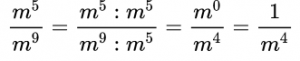
В каждой части дроби содержатся разные многочлены, поэтому сократить пока дробь мы не можем, так как нет множителей. Значит, по возможности, мы должны найти выражение, которое можно разложить на множители, это знаменатель, так как можем вынести за скобки общий множитель х(х – у). Только потом мы можем сократить дробь на одно и то же выражение – многочлен (х – у).

Пример №4. Сократим дробь:

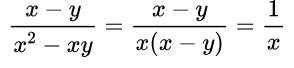
Здесь мы видим, что в числителе многочлен, а в знаменателе произведение одночленов и многочлена, причем многочлены различны. Значит, надо сделать так, чтобы числитель и знаменатель содержали одинаковые множители. Числитель можно разложить на множители по формуле разности квадратов, то есть m 2 – n 2 =(m–n)(m+n), затем сократить дробь на одно и то же выражение (m–n).

Сложение и вычитание алгебраических дробей с одинаковым знаменателем

При сложении и вычитании алгебраических дробей с одинаковыми знаменателями знаменатель остается прежним, а числители складывают или вычитают (из числителя первой вычитают числитель второй дроби).

Пример №5. Выполним сложение дробей:

Здесь одинаковые знаменатели, поэтому записываем его, а числители складываем: при сложении видим подобные слагаемые, которые приводим и получаем в числителе 5х.

Пример №6. Выполним вычитание дробей:

В знаменатель записываем 2х, а из числителя первой дроби вычитаем числитель второй дроби, при этом не забываем вычитаемое взять в скобки, если оно является многочленом. Затем раскрываем скобки, помня о том, что необходимо поменять знаки на противоположные, так как перед ними стоит знак «минус». Затем приводим подобные слагаемые и получаем новый числитель.

Сложение и вычитание алгебраических дробей с разными знаменателями

Чтобы сложить или вычесть дроби с разными знаменателями, необходимо:

Пример №7. Выполнить сложение дробей:

Чтобы найти общий знаменатель, надо найти для чисел 5 и 10 наименьшее общее кратное (наименьшее число, которое делится и на 5, и на 10), это число 10. В первом знаменателе есть еще множитель – переменная у, поэтому также берем у для общего знаменателя. Таким образом, у нас есть два множителя 10 и у, это и есть наш общий знаменатель.

Теперь находим дополнительный множитель к каждой дроби. Для этого общий знаменатель 10у делим на первый знаменатель 5у, получим 2, значит, умножаем на 2 первый числитель 2х. Для второй дроби 10у делим на 10, получаем у, умножаем на него числитель второй дроби – с. Получаем в числителе 4х+су.

Пример №8. Выполнить вычитание дробей:

Здесь знаменатели дробей различные многочлены, поэтому надо рассмотреть каждый. Первый знаменатель – это формула сокращенного умножения, по ней можно разложить на множители данный многочлен а 2 – с 2 =(а–с)(а+с). Второй знаменатель представляет собой простой многочлен, который нельзя разложить на множители. Составим новый знаменатель, состоящий из разных выражений – это (а–с)(а+с).

Находим дополнительные множители: к первой дроби дополнительного множителя нет, так как новый общий знаменатель – это полностью знаменатель первой дроби. А ко второй дроби это будет выражение (а – с). Поэтому умножаем числитель 2 на (а – с).

Приводим подобные слагаемые, а полученную дробь сокращаем на выражение (а+с).

Умножение алгебраических дробей

Чтобы перемножить алгебраические дроби, надо числитель перемножить с числителем, а знаменатель со знаменателем. При необходимости выполнить сокращение алгебраической дроби, используя правило.

Пример №9. Выполнить умножение дробей:

Здесь перемножаем числители и знаменатели, полученную дробь сокращаем на 2с.

Пример №10. Выполнить умножение дробей:

Здесь в числителях и знаменателях — многочлены. Поэтому при записи умножения обязательно заключаем их в скобки. При этом мы видим, что числитель и знаменатель содержат одинаковые множители – многочлены (х+2), поэтому можно сократить дробь на этот многочлен.

Деление алгебраических дробей

Чтобы разделить одну алгебраическую дробь на другую, надо первую дробь умножить на дробь, обратную второй (то есть умножить на дробь, у которой числитель равен знаменателю второй дроби, а знаменатель числителю второй дроби). Далее – выполнить умножение дробей по уже известному алгоритму.

Пример №11. Выполнить деление дробей:

Здесь выполним деление по алгоритму: перейдем от деления к умножению на дробь, обратную делителю. Сократим полученную дробь на выражение (a+b) и на 2.

Найдите значение выражения:

Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:

теперь переходим от деления дробей к их умножению:

затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:

сокращаем выражение на (a–5b): Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений): Подставим полученные значения в выражение и найдем конечный результат: Ответ: 39

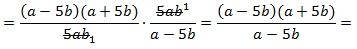
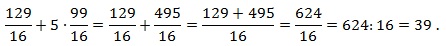
pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения при x = 12:

Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:

далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):

теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:

Подставляем числовое значение для х в полученное выражение и находим результат:

Ответ: 0,6

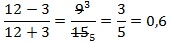
pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения

В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:

Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:

Вычислим её значение, подставив числа из условия:

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения:

Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:

Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:

5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x

Тогда дробь примет вид:

Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y

Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник