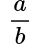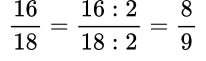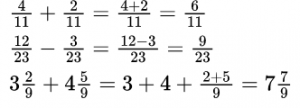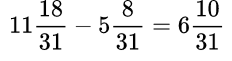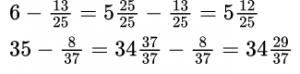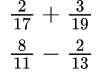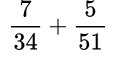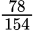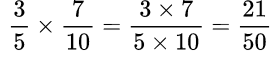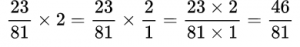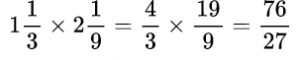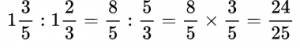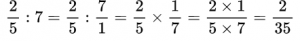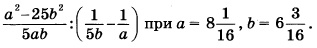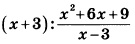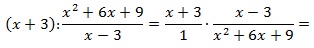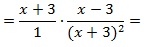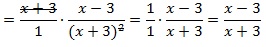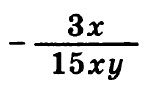Как решать дроби пояснение
Как решать дроби. Решение дробей.
В статье покажем, как решать дроби на простых понятных примерах. Разберемся, что такое дробь и рассмотрим решение дробей!
Понятие дроби вводится в курс математики начиная с 6 класса средней школы.
В первом случае торт разрезали поровну и взяли одну половину, т.е. 1/2. Во втором случае торт разрезали на 7 частей, из которых взяли 4 части, т.е. 4/7.
Если часть от деления одного числа на другое не является целым числом, ее записывают в виде дроби.
Например, выражение 4:2 = 2 дает целое число, а вот 4:7 нацело не делится, поэтому такое выражение записывается в виде дроби 4/7.
Иными словами дробь — это выражение, которое обозначает деление двух чисел или выражений, и которое записывается с помощью дробной черты.
Например, 5 целых 3/4.
Данная запись означает, что для того, чтобы получить целую 6 не хватает одной части от четырех.
Если вы хотите запомнить, как решать дроби за 6 класс, вам надо понять, что решение дробей, в основном, сводится к понимаю нескольких простых вещей.
Как решать дроби. Примеры.
К дробям применимы самые разные арифметические операции.
Приведение дроби к общему знаменателю
Например, необходимо сравнить дроби 3/4 и 4/5.
Чтобы решить задачу, сначала найдем наименьший общий знаменатель, т.е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей
Наименьший общий знаменатель(4,5) = 20
Затем знаменатель обоих дробей приводится к наименьшему общему знаменателю
Ответ: 15/20 Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Я вообще не умею решать дроби, но понятие немного есть. И поэтому стараюсь как можно скорее научиться решать дроби как дважды два четыре. Мне легче с формулами сложные примеры решить чем решать дроби!
говорит та самая красотка которая не навидит дроби
Обыкновенные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доля целого
Доля — это каждая равная часть, из суммы которых состоит целый предмет.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:
Понятие дроби
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
Виды дробей:
Какие еще бывают дроби:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.
Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:
где a, b, k — натуральные числа.
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Полученные числа запишем справа сверху над числителем.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо:
Дроби и действия с дробями
Что такое дроби?
Вспоминаются примеры из начальной школы. Представьте себе пирог вкусный такой, и 4 голодных ребенка.
Как бы им так сделать, чтоб пирога досталось всем? Верно, надо его поделить, поделить один пирог на 4 человека:
На рисунке ты видишь пирог, разрезанный на 4 дольки. Так вот, как раз дробь – это и есть доля от целого.
Сегодня мы разберем подробно, что такое дроби. Как их правильно делить, умножать, вычитать, складывать, преобразовывать…
В общем, сегодня ты узнаешь о дробях ВСЕ, что нужно знать для успешной сдачи ОГЭ или ЕГЭ.
Дроби — коротко о главном
Определения:
Простая дробь (обыкновенная дробь) – запись рационального числа в виде отношения двух чисел \(\displaystyle\frac\).
Делимое \(\displaystyle a\) – числитель дроби, а делитель \(\displaystyle b\) – знаменатель дроби.
Правильная дробь – дробь, у которой числитель меньше знаменателя.
Например: \(\displaystyle\frac<2><5>\), \(\displaystyle\frac<1><7>\) и так далее.
Неправильная дробь –дробь, у которой числитель больше или равен знаменателю.
Например: \(\displaystyle\frac<9><5>\), \(\displaystyle\frac<13><2>\) и так далее.
Смешанная дробь – дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.
Например: \(\displaystyle2\frac<2><5>\)\( \displaystyle \displaystyle=\frac<2\cdot 5><5>+\frac<2><5>=\frac<10><5>+\frac<2><5>=\frac<12><5>\).
Десятичная дробь – обыкновенная дробь со знаменателем \(\displaystyle10\), \(\displaystyle100\), \(\displaystyle1000\) и так далее, (т.е. \(\displaystyle<<10>^
>\), где \(\displaystyle n\) — натуральное число).
Например: \(\displaystyle\frac<9><100>\) в виде десятичной дроби записывается как \(\displaystyle0,09\),
\(\displaystyle\frac<225><1000>\) записывается как \(\displaystyle0,225\).
Основное свойство дроби:
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, дробь не изменится, несмотря на то, что выглядеть она будет по-другому.
Действия с дробями:
Сложение/вычитание дробей
Умножение дробей
Деление дробей
Сокращение дроби
Приведение дробей к наименьшему общему знаменателю
Например: \(\displaystyle\frac<1><3>\) и \(\displaystyle\frac<3><4>\). Наименьший общий знаменатель — \(\displaystyle12\).
Дополнительный множитель первой дроби — \(\displaystyle12:3=4\), дополнительный множитель второй дроби — \(\displaystyle12:4=3\).
Следовательно: для первой дроби: \(\displaystyle\frac<1\cdot 4><3\cdot 4>=\frac<4><12>\), для второй дроби: \(\displaystyle\frac<3\cdot 3><4\cdot 3>=\frac<9><12>\).
Преобразования неправильной дроби в смешанную дробь
Например: \(\displaystyle\frac<17><4>\) = \(\displaystyle4\frac<1><4>\).
Сравнение дробей:
Простые дроби
В данном случае от целого куска в сторонке отделенная одна доля, одна из четырех, одна четвертая.
Это простая дробь.
Простые дроби принято записывать одним из следующих способов: \(\displaystyle \frac<1><4>\), \(\displaystyle <1>/<4>\;.\)
Ты не поверишь, все эти записи означают одно и то же – одна четвертая. А что останется если забрать эту \(\displaystyle 1/4?\) Было \(\displaystyle 4\) из \(\displaystyle 4\), или \(\displaystyle 4/4\), забрали \(\displaystyle 1/4\).
Верно, останется \(\displaystyle 3\) дольки, \(\displaystyle 3\) из \(\displaystyle 4\). Запишем, как полагается, \(\displaystyle 3/4\).
Можно даже вот так: \(\displaystyle 4/4-1/4=3/4\)
То, что находится выше черты – это числитель (ну или слева от черты в такой записи как тут), то, что ниже – знаменатель.
Можно запомнить так: Ч – чердак. Числитель сверху 🙂
Примеры простых дробей: \(\displaystyle 1/5,\text< >2/4,\text< >3/10,\text< >17/3.\)
Правильные и неправильные простые дроби
В этом ряду все дроби правильные, в них числитель меньше знаменателя. Кроме одной. Да-да, ты не ошибся, бывает и такое, что числитель больше знаменателя, как в этой дроби, например: \(\displaystyle 17/3\).
Если числитель больше знаменателя, то дробь называется неправильной.
Вне зависимости от того правильная дробь или неправильная, она будет простой.
Давай остановимся на неправильной дроби \(\displaystyle 17/3\). Что же это она неправильная?
Вспоминай пример с пирогом, там была \(\displaystyle 1/4\) – одна часть из четырех, а тут что получается? \(\displaystyle 17\) частей из \(\displaystyle 3\)?
Бред какой-то! У нас в знаменателе число, которое означает, что весь пирог состоит из стольки частей! Берем \(\displaystyle 4\) части и поучаем целый ровненький пирог. Но числитель говорит, что на данный момент у нас есть лишь одна из этих частей.
А \(\displaystyle 17/3\)?
Что же, у нас есть \(\displaystyle 17\) частей, а для целого пирога в данном случае надо \(\displaystyle 3\) части. Ну так давай соберем из кусочков целые пироги и отдельно их поставим.
Как узнать сколько пирогов мы можем получить из \(\displaystyle 17\) частей? Верно, надо на \(\displaystyle 3\) как раз и поделить.
Если попробовать составить \(\displaystyle 6\) пирогов, т.е. \(\displaystyle 3\cdot 6=18\), надо \(\displaystyle 18\) частей. Не хватает. А \(\displaystyle 3\cdot 5=15\), о, хватило! Получается \(\displaystyle 5\) целых пирогов собрали, положили в сторону. Осталось \(\displaystyle 17-3\cdot 5=2,2\), \( \displaystyle 2\) куска.
А для целого пирога надо \( \displaystyle 3\) части. В итоге у нас \( \displaystyle 5\) целых и \( \displaystyle 2/3\) (две третьих) пирога.
Много места занимает такое обозначение. А что если убрать лишние слова и оставить только \( \displaystyle 5\frac<2><3>\) (пять целых и две третьих).
Смешанная дробь
То, что у нас получилось (\( \displaystyle 5\frac<2><3>\)), называют смешанная дробь – дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.
То, что между \( \displaystyle 5\) пирогами и \( \displaystyle 2/3\) пирога нет никакого знака не говорит о том, что там знак умножения, как если бы мы писали \( \displaystyle 2x\).
Запомни, между целой и дробной частями можно поставить знак плюс, вот так: \( \displaystyle 5\frac<2><3>=5+\frac<2><3>\).
Так же можно проделать и обратное действие, т.е. преобразование из смешанной дроби в неправильную дробь.
Ты же знаешь, как это сделать?
Преобразование из смешанной дроби в неправильную дробь.
В результате получим исходное \( \displaystyle 17/3\).
Обыкновенные дроби
теория по математике 📈 числа и вычисления
Обыкновенная дробь – это запись числа в виде:
где число a называют числителем, а число b – знаменателем дроби.
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Пример №1. У первой дроби можно разделить числитель и знаменатель на одно и то же число 14, и получится равная ей дробь. Или как у второй дроби можно умножить числитель и знаменатель на одно и то же число, допустим, на 5.
Сократить дробь – значит разделить числитель и знаменатель на одно и то же число.
Пример №2. Чтобы сократить данную дробь надо вспомнить признаки делимости и увидеть, что числитель и знаменатель дроби — четные числа, значит, их можно разделить на 2, то есть дробь сокращается на 2:
Пример №3. По признаку делимости числитель и знаменатель делятся на 5, значит, сокращается данная дробь на 5.
Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
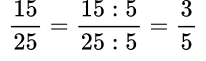
При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями нужно знаменатель оставить тем же, а числители сложить (вычесть). Если дроби смешанные, то отдельно складывают (вычитают) целые части.
Решения можно записывать короче, выполняя устно сложение или вычитание целых частей, а также – числителей.
Вычитание обыкновенной дроби из целого числа
Чтобы вычесть дробь из единицы, нужно единицу представить в виде неправильной дроби, числитель и знаменатель которой равны знаменателю вычитаемой дроби.
Пример №5. Представляем единицу в виде дроби и получаем вычитание дробей с одинаковыми знаменателями (числители можно вычесть устно).
Вычитание обыкновенной дроби из бóльшего числа
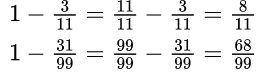
Чтобы вычесть обыкновенную дробь из числа, большего 1, необходимо представить эту дробь в виде смешанного числа, числитель и знаменатель которой равны также знаменателю вычитаемой дроби.
Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями требует предварительного приведения дробей к общему знаменателю. Существуют несколько приемов, которыми можно воспользоваться для нахождения общего знаменателя.
Нахождение общего знаменателя
Наименьшее общее кратное (НОК) – это наименьшее число, которое делится без остатка на данные знаменатели одновременно. Обычно его находят устно при выполнении действий с дробями.
Правило нахождения НОК рассмотрим на примере чисел 12 и 15. Пример №7. 1. Нужно разложить на простые множители каждое число:
2. Затем найти одинаковые множители (подчеркиваем):
В данном случае это только множитель 3.
3. Взять одно из данных чисел и домножить на оставшиеся (не подчеркнутые) множители другого числа:
12 домножаем на 5: 12×5=60, или
15 домножаем на 2 и 2: 15×2×2=60
Таким образом, НОК =60. Обычно достаточно просто внимательно посмотреть на числа и в уме подобрать для них НОК.
Перемножение знаменателей. Приём №2.
Нам необходимо просто перемножить знаменатели. Обычно этот прием используется тогда, когда даны простые числа (которые делятся на 1 и на само себя) и на множители их не разложить.
Пример №8. 
Для нахождения общего знаменателя в первом случае: 17×19=323, во втором: перемножаем 11 и 13, получаем 143.
Последовательный подбор. Приём №3.
Данный способ можно применить для небольших чисел устно: возьмем больший из знаменателей, умножим его на 2 и проверим, делится ли это число на второй знаменатель. Если нет, то умножим последовательно на 3, 4 и проверим аналогично.
Пример №9. Возьмем число 51, умножим на 2, получим 102 — видим, что 102 делится на 34, поэтому 102 и будет общий знаменатель.
После того, как мы научились находить общий знаменатель, приступаем непосредственно к алгоритму сложения (или вычитания) обыкновенных дробей с разными знаменателями.
Находим общий знаменатель. Можно использовать прием, когда умножаем 11 и 14, так как 11 — простое число. Следовательно, общий знаменатель равен 154. Находим дополнительный множитель к каждому числителю:
Выполняем умножение в числителе: 
Выполняем сложение дробей с одинаковыми знаменателями: 
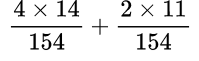
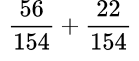
Умножение обыкновенных дробей
При умножении обыкновенных дробей получают дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
При умножении обыкновенной дроби и целого числа необходимо целое число представить в виде дроби, числитель которой равен этому числу, а знаменатель равен 1 (что по сути означает перемножение числителя единственной первой дроби и целого числа, знаменатель же остается от первой дроби, так не меняется при умножении на единицу).
Если даны смешанные дроби, то необходимо сначала смешанную дробь перевести в неправильную, а затем выполнить умножение.
Пример №11. Здесь числитель 3 умножили на числитель 7, знаменатель 5 на знаменатель 10.
Пример №12. Случай, когда мы находим произведение дроби и целого числа. Целое число представили в виде дроби со знаменателем 1.
Пример №13. Нам даны смешанные дроби, переводим их в неправильные для выполнения умножения.
Деление обыкновенных дробей
При делении обыкновенных дробей необходимо делимое (то есть первую дробь) умножить на перевернутую вторую дробь, то есть дробь, обратную второй.
Если даны смешанные числа, то перед выполнением деления их необходимо перевести в обыкновенные неправильные дроби.
Если дробь нужно разделить на целое число, то его сначала нужно представить в виде дроби, а затем выполнить деление по правилу.
Пример №14. Делимое умножаем на число, обратное делителю.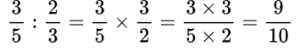 
Пример №15. Смешанные дроби сначала переводим в неправильные, а затем выполняем деление. 
Пример №16. Деление дроби на целое число, где целое число 7 представлено в виде обыкновенной дроби.
Найдите значение выражения:
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:
теперь переходим от деления дробей к их умножению: 
затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:
сокращаем выражение на (a–5b): 
Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений): 
Подставим полученные значения в выражение и найдем конечный результат: 
Ответ: 39
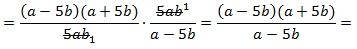
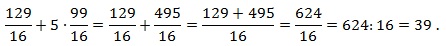
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения при x = 12:
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
Подставляем числовое значение для х в полученное выражение и находим результат:
Ответ: 0,6
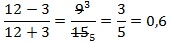
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:
Вычислим её значение, подставив числа из условия:
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:
Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:
5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x
Тогда дробь примет вид:
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y
Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.
Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй — в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:
Далее выносим из числителя второй дроби a:
Подставляем значение a = 13:
pазбирался: Даниил Романович | обсудить разбор | оценить
Какое из данных ниже чисел является значением выражения?
Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:
Суммарно наши действия выглядят так:
pазбирался: Даниил Романович | обсудить разбор | оценить
Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:
1/21 + 1/28 = 4/84 + 3/84
Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:
1 / ( 7 / 84 ) = 1 •84/7 = 84/7
Далее остается поделить 84 на 7:
pазбирался: Даниил Романович | обсудить разбор | оценить
Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.
Проведя вычисления в скобках, получим:
pазбирался: Даниил Романович | обсудить разбор | оценить